紗線截面壓縮變形仿真與驗證

李冠志, 趙 強, 汪 軍, GONG Hugh

(1. 東華大學 紡織學院， 上海 201620； 2. 中國紡織科學研究院， 北京 100025； 3. 東華大學紡織面料技術教育部重點實驗室， 上海 201620； 4. 曼徹斯特大學 材料學院, 曼徹斯特 M60 1QD)

紗線截面壓縮變形仿真與驗證

李冠志1,2, 趙 強1,2, 汪 軍1,3, GONG Hugh4

(1. 東華大學 紡織學院， 上海 201620； 2. 中國紡織科學研究院， 北京 100025； 3. 東華大學紡織面料技術教育部重點實驗室， 上海 201620； 4. 曼徹斯特大學 材料學院, 曼徹斯特 M60 1QD)

為了改進現有紗線條干均勻度測試儀在預測織物外觀質量上的缺陷，對棉型平紋織物織造過程中的紗線截面面積、紗線截面周長、纖維空隙率、紗線壓扁率, 紗線密度等紗線截面參數的變化建立分析模型并優選參數，并采用有限元分析和實驗論證的方法，進一步分析織造過程中紗線截面面積及周長的變化。通過分析得出，在紗線到織物的織造變形過程中，紗線截面周長的變化遠小于其截面面積的變化，紗線截面面積的變化率約是紗線截面周長變化率的2～3倍。通過對紗線截面橢圓長軸與其截面周長、截面面積分別進行相關性分析，得出紗線截面周長與橢圓長軸呈弱相關，紗線截面面積與長軸間無相關性。

紗線條干均勻度； 紗線壓扁率； 有限元分析； 圖像處理

紗線截面形狀(紗線外觀條干不勻)對織物外觀有重要影響，在1969年Hearle教授認為紗線截面形狀是不規則多邊形[1]，這種紗線截面形狀的差異本質上是紗線徑向上纖維分布不勻。單紗經歷織造工序，受力拉伸、彎曲、扭轉和壓縮交織成織物后，纖維分布不勻現象加劇，其截面形狀的變化將更大，從而進一步影響織物外觀質量。

一直以來，利用單紗質量來實現織物質量的準確預測是極具挑戰性的。USTER公司電容式紗線條干均勻度測試儀[2]測得的條干數據用于預測織物外觀質量，單紗經過織造過程織成織物后，紗線截面的纖維根數基本不變，但是對織物外觀造成影響的不僅有紗線中纖維根數，還有纖維間空隙，這二者共同決定了紗線外觀直徑；因此，電容式條干儀在預測織物外觀質量方面不可避免地存在缺陷。為此，近年來業內各式電容式條干儀紛紛加裝了測量紗線外觀直徑的光電模塊用之于織物仿真[2]，或利用圖像式紗線外觀測試分析儀器預測布面質量[3-5]。上述改進雖然預測效果略有提高，但尚不能完全滿足生產實際要求。

究其原因，以往的方法均是紡紗廠從生產控制的視角來評價紗線綜合質量，很少從織物外觀角度來評價紗線外觀質量，深究單紗經過織造過程后影響織物外觀的紗線截面參數變化，這些參數是建立起由紗線質量到布面質量準確預測和一致性評價的關鍵。本文依據相關學者關于單紗紗線截面模型[6-8]、織物中紗線截面模型[9-13]和紗線壓縮變形[14-15]的研究成果，結合紗線質量與布面質量的一致性評價需要，將單紗和織物中的紗線截面模型統一假定為橢圓形。通過研究織造過程中影響織物外觀的紗線截面參數的變化，探索改進現有織物外觀質量預測方法的新思路。

1 理論分析

1.1 理論分析及參數選取

在織造過程中，紗線截面受力拉伸、彎曲、扭轉和壓縮而變形，在這一過程中紗線截面參數是不斷變化的，這些參數主要有紗線截面面積Sy、截面周長Sp、纖維空隙率Vf、紗線壓扁率f, 紗線密度ρy,下面探究紗線這些截面參數在織物中的變化規律。

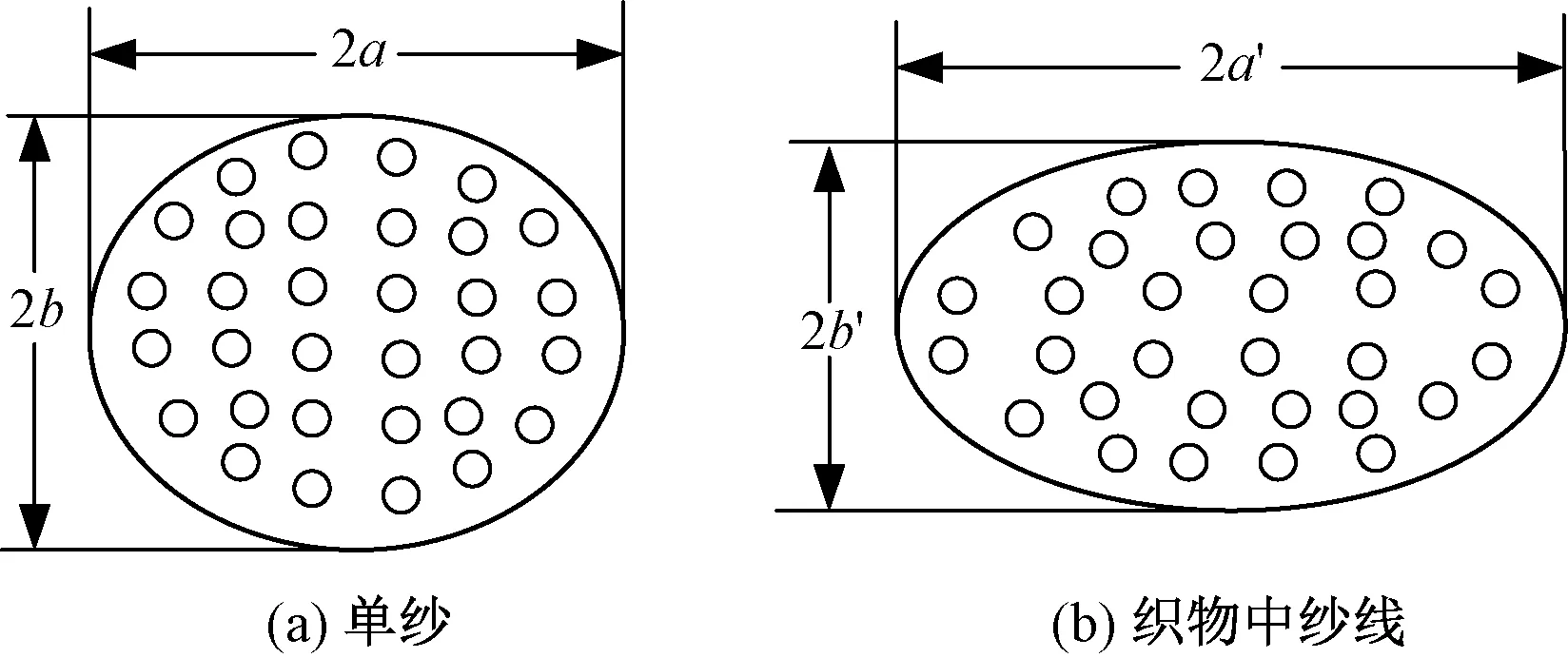
圖1 紗線截面模型Fig.1 Yarn cross-section model. (a) Individual yarn; (b) Yarn in fabrics

假設織造前后紗線中的纖維不發生軸向的滑移，且纖維根數n，纖維截面積Sf，纖維密度ρf均不變。

(1)

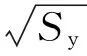
綜上可以看出，Vf、ρy均由Sy所決定。而Sp由Sy和f的共同決定，所以，這里紗線截面參數主要考慮Sy和紗線截面周長Sp即可。

Sy和Sp由最外圍纖維排列所決定的，這里假設最外圍纖維相互間緊密排列。此時，紗線截面形態的變化與外圍纖維所圍繞成閉合區域的纖維空隙率Vf有較大關系。圖2示出紗線壓縮形變分析。當閉合區域的Vf最小時：纖維如圖2(a)所示緊密排列，在紗線受壓變形過程中，外圍纖維所擬合成橢圓截面后得到的Sp呈現增大趨勢，Sy基本不變，如圖2(b)所示；當閉合區域Vf最大時，外圍纖維如圖2(c)所示緊密環繞排列，紗線受壓變形過程中，若外圍纖維仍緊密排列，不向內部坍縮滑移，則最終Sp基本不變，Sy減小，如圖2(d)所示；若發生坍縮內移，則最終Sp減小，Sy減小如圖2(f)所示；交織過程中紗線形態應是形態1，形態2和形態3這3種情況之一。

Sy和Sp在織物中的變形主要是由紗線受力所造成的，這些力的作用時間和大小受到紗線性質、上機工藝、織物組織結構等較多復雜因素的影響。為了探究紗線在織造過程中截面參數的變化，下面以棉型織物為例利用有限元分析的方法初步探究。

圖2 紗線壓縮形變分析Fig.2 Analysis of yarn compression. (a) F1 before compress; (b) F1 after compress; (c) F2 before compress; (d) F2 after compress; (e) F3 before compress;(f) F3 after compress

1.2 模型建立及仿真

建立織物模型時本文以18 tex的棉紗織造的平紋織物為參照樣，其經向緊度16°，緯向緊度12°。假設構成織物的紗線是由60根纖維堆砌而成的，紗線截面模型長軸2a=0.2 mm，短軸2b=0.18 mm。Abaqus軟件[16]中設置的紗線參數如表1所示，織物交織仿真應變云圖見圖3。定義緯紗方向3根紗線依次按交織規律相對運動，相對位移為0.42 mm。下面分析交織過程中時間對最中間經紗對交織點處紗線的截面周長和截面面積的影響，結果如圖4所示。從該圖中可看出在交織受壓過程中，紗線截面周長的變化率小于截面面積。這里用極差系數(見下式)來表示交織前后的變化率，圖4中，交織前后紗線周長減小了9.02%，而面積減小了27.67%。

(2)

式中：J為極差系數，Xmax為形變前后周長或面積最大值，Xmin形變前后周長或面積最小值。

表1 紗線參數設置Tab.1 Yarn parameters in abaqus

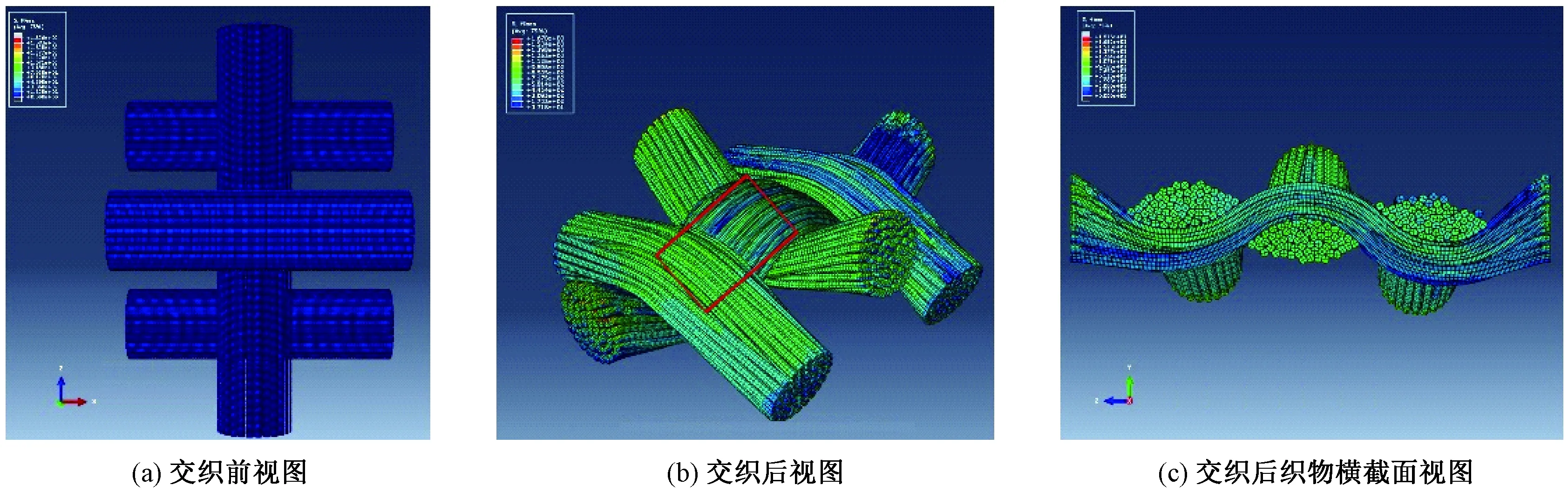
圖3 織物交織仿真應變云圖Fig.3 Contours of the fabric weaving modeling. (a) Before weaving; (b) After weaving; (c) Section view of weaved fabric.

交織完成后選取半個單胞進行分析，如圖3(b)中紅色框選部分所示，等間隔選取10個紗線截面，如圖5所示，分別計算紗線截面周長和截面面積，同樣得出了類似的變化規律，結果如圖6所示，壓縮前后紗線周長減小了7.54%，而面積減小了17.34%。

圖4 織物交織過程中紗線截面參數隨時間變化Fig.4 Yarn cross-section parameter variations with time during fabric weaving process.

2 實驗部分

2.1 織物中紗線截面圖像的獲取

連續獲取織造全部過程中的紗線截面變化是極其困難的，但考慮到紗線截面變形主要是與紗線受力有關，織物中單根紗線交織處和非交織處受力不同必然造成紗線截面形變不同。下面通過研究織物中紗線所處不同位置的截面形狀變化來研究紗線截面周長和紗線截面面積的變化規律。

實驗材料選用棉紗交織成的平紋織物，該織物由Bonas-Varitex織機織造，經紗緊度16°，緯紗緊度12°，紗線線密度18 tex，紗線捻度890 捻/10 cm，該紗線是由馬克隆值為4.2的棉纖維紡制而成。為保證圖像數據的非破壞采集，采用法國的同步輻射光源ESRF中ID19光束掃描織物，利用2 048像素×2 048像素分辨率的FReLoN相機對織物進行成像，圖像分辨率為18 149像素，每幅圖像對應的實物大小為2.8 mm×2.8 mm。下面隨機選取1/2個單胞圖像進行分析，圖7所示。

圖5 織物交織后同一紗線不同截面Fig.5 Different section views of the same yarn in fabric. (a) Section 1; (b) Section 2; (c) Section 3; (d) Section 4; (e) Section 5; (f) Section 6; (g) Section 7; (h) Section 8; (i) Section 9; (j) Section 10

圖6 交織為織物后同一根紗線紗線不同位置截面參數變化Fig.6 Yarn cross-section parameter variations at different section views of the simulated yarn

圖7 織物中同一紗線不同位置截面形狀變化Fig.7 Yarn cross-section parameter variations at different section views of the same yarn in a real fabric. (a) Section 1; (b) Section 2; (c) Section 3; (d) Section 4; (e) Section 5; (f) Section 6; (g) Section 7; (h) Section 8; (i) Section 9; (j) Section 10

2.2 紗線截面圖像紗線周長和面積的提取

紗線截面圖像首先進行中值濾波的降噪處理，二值化、閉運算后，為消除閉運算后圖像有部分黏連。利用分水嶺算法(watershed)再次分割，并調用imimposemi函數過濾掉一些特別小的局部最小分割區域。分割完成后然后調用bwareaopen函數消除較小的閉合面積，并選用canny算子進行邊緣檢測，從而得到清晰的紗線外沿輪廓。最后根據該輪廓調用fitellipse函數進行橢圓擬合，計算出橢圓長軸和短軸長度，流程如圖8所示。

圖8 紗線截面參數提取Fig.8 Extraction of yarn cross-section parameters: (a)Original; (b)Median; (c)Binaryzation; (d)Imclose; (e)Watershed; (f)Bwareaopen; (g)Eage detection; (h)Ellipse fitting

3 結果分析

對上述紗線截面1～10依次進行處理后，得到表2中數據，從表中f可以看出，f在交織點處最小，壓扁最厲害；而兩交織點中間最大，即該處更接近于圓形。f由交織點中間向交織點處移動的過程中呈現不斷減小的趨勢。在此過程中，橢圓紗線截面的面積和周長也呈減小趨勢，由圖9可以明顯看出紗線截面周長的減小趨勢相較于紗線截面面積則更為平緩。通過表2計算極差系數，交織前后紗線周長減小了17.33%，而面積減小了41.60%，與仿真結論趨勢一致，但比仿真結果偏大，其原因是仿真過程中假定各紗線截面均相等，纖維截面為標準圓形且纖維間等距離堆砌，這些理想化假設與實際情況均有差異。

為進一步佐證，本文用同樣方法計算了Hirai[14-15]中壓縮紗線后紗線截面圖像的紗線截面周長和紗線截面面積數據，得出5、50、1 000 cN這3種拉力下的紗線壓縮前后紗線周長減小了12.24%，而面積減小了35.81%，這一變化趨勢與在紗線壓縮時表現出的特性保持一致，且與仿真結果趨勢一致。

表2 織物組織中不同截面紗線截面參數Tab.2 Yarn cross-section parameters of different yarn cross sections in a fabric.

圖9 紗線截面周長和紗線截面面積變化Fig.9 Yarn cross-section perimeter and area variations of section 1-10

織物中尤其經緯密較大的織物，其紗線在交織點處呈壓扁狀態，織物外觀主要受到被壓紗線截面的橢圓長軸影響[7]。下面分別對紗線截面周長和截面面積與紗線截面長軸進行相關性分析，圖10示出紗線截面周長與橢圓長軸呈弱相關，相關系數R=0.2，而紗線截面面積與長軸無相關性，R=0.07。因此，紗線截面周長預測織物質量時相對于紗線截面面積更有優勢。

圖10 紗線截面周長與截面面積與橢圓長軸相關性分析Fig.10 Correlation analysis of ellipse major axes with yarn cross-section perimeter and area of sections 1-10

4 結 論

在橢圓形紗線截面模型的基礎上，本文根據有限元分析和實驗論證，得出以下幾點結論。

1)紗線在交織為織物受擠壓變形的過程中，紗線外圍纖維傾向于坍縮內移(形態3)，紗線截面周長和截面面積在這一過程中均減小。

2)紗線交織受壓變形過程中受影響的紗線截面參數中紗線截面面積、紗線截面周長、纖維空隙率、紗線壓扁率, 紗線密度，最終可簡化為紗線截面周長和紗線截面面積這兩個參數。

3)截面周長和紗線截面面積在紗線到織物的變形過程中，紗線截面周長的變化遠小于紗線截面面積的變化，紗線截面面積的變化約是紗線截面周長變化的2～3倍，紗線截面周長的變化率在8%～17%之間，紗線截面面積的變化率在17%～42%之間。

4)織物外觀主要受到織物中被壓紗線橢圓截面的長軸所影響，數據表明，紗線截面周長與橢圓長軸呈弱相關，紗線截面面積與紗線橢圓截面的長軸無相關性，紗線截面周長在預測織物質量時相對于紗線截面面積更有優勢。

這些結論有助于改善紗線質量到布面質量客觀一致性評價，對改進現有織物外觀質量預測手段提供了新思路。

FZXB

[1] HEARLE J W, GROSBERG P, BACKER S. Structural Mechanics of Fibers, Yarns, and Fabrics[M]. New York: Wiley-Interscience, 1969:175-211.

[2] USTER?TESTER 5 Brochure[EB/OL]. [2016-05-01]. http://www.uster.com/fileadmin/customer/Knowle-dge/Textile_Know_How/Yarn_testing/U_T5_S800_High_sped_testing_in_01.pdf.

[3] Electronic inspection board[EB/OL].[2016-07-01]. http://www.lawsonhemphill.com/assets/lh-481-eib-s.pdf.

[4] 劉長伴. CTT在紗線綜合質量評價中的應用研究[D]. 天津: 天津工業大學, 2007: 64-65. LIU Changban. The study of yarn comprehensive evaluation with CTT system[D]. Tianjin: Tianjin Polytechnic University, 2007: 64-65.

[5] CARVALHO V, GON?PALVES N, SOARES F, et al. An overview over yarn mass parameterization me-thods[C]//Sensordevices 2011, The Second International Conference on Sensor Device Technologies and Applications. Nice: [s.n.]. 2011: 18-24.

[6] TSAI I, CHU W. The measurement of yarn diameter and the effect of shape error factor (SEF) on the measurement of yarn evenness[J]. Journal of the Textile Institute, 1996, 87(3): 496-508.

[7] GüNAY M. Characterization and quantification of woven fabric irregularities using 2-D anisotropy measures[D]. NC: North Carolina State University, 2005: 74-75.

[8] HAMILTON J B. A direct method for measuring yarn diameters and bulk densities under conditions of thread flattening[J]. Journal of the Textile Institute Transactions, 1959, 50(12): 655-672..

[9] PEIRE F T. The geometry of cloth structure[J]. Journal of the Textile Institute Transactions, 1937, 28(3): 11-22.

[10] KEMP A. An extension of Peirce′s cloth geometry to the treatment of non-circular threads[J]. Journal of the Textile Institute Transactions, 1958, 49(1): 44-48.

[11] SHANAHAN W J, HEARLE J W S. An energy method for calculations in fabric mechanics: part II: examples of application of the method to woven fabrics[J]. Journal of the Textile Institute, 1978, 69(4): 92-100.

[12] GONG R H, OZGEN B, SOLEIMANI M. Modeling of yarn cross-section in plain woven fabric[J]. Textile Research Journal, 2009, 79(11): 1014-1020.

[13] OZGEN B, GONG R H. Modelling of yarn flattening in woven fabrics[J]. Textile Research Journal, 2011, 81(15): 1523-1531.

[14] HIRAI T, FUKAI S, SENBA T. Yarn tensile property for analysis: finite element analysis on the biaxial tensile properties of woven fabrics(part 2)[J]. Journal of the Textile Machinery Society of Japan Transactions, 1982, 35: 79-86.

[15] HIRAI T, SENBA T, IBARAKI N. Application to design of woven fabrics: finite element analysis on the biaxial tensile properties of woven fabrics(part 3)[J]. Journal of the Textile Machinery Society of Japan Transactions, 1982, 35: 87-96.

[16] LIN H, SHERBURN M, CROOKSTON J, et al. Finite element modelling of fabric compression[J]. Model-ling & Simulation in Materials Science & Engineering, 2008, 16(3):697-704.

Modeling and experimental study on yarn′s cross-section compression deformation

LI Guanzhi1,2, ZHAO Qiang1,2, WANG Jun1,3, GONG Hugh4

(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.ChinaTextileAcademy,Beijing100025,China; 3.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,Shanghai201620,China； 4.SchoolofMaterials,UniversityofManchester,ManchesterM60 1QD,UK)

In order to overcome drawbacks of the conventional yarn evenness tester in predicting fabric appearance quality, this paper presents the characterization of the individual yarn deformation and its influence on the resulting quality of the fabric appearance. In the model, the yarn deformation parameters such as the cross-sectional area, the yarn cross-sectional perimeter, the void ratio, the yarn flattening ratio f and yarn density were evaluated. Using mathematical modeling, the cross-sectional area and perimeter were presumed as the critical yarn cross-sectional parameters for predicting the fabric appearance quality. Then the finite element modeling (FEM) method and experiment verification were performed to analyze the variation of the cross-sectional area and perimeter in the process of weaving. The results show that the cross-sectional area varhes almost 2 to 3 times greater than the cross-sectional perimeter. The correlation analysis among the major ellipse radius, the cross-sectional perimeter, and the cross-sectional area are further conducted. The findings reveal a weak correlation between major ellipse radius and cross-sectional perimeter, while major ellipse radius and cross-sectional area are uncorrelated.

yarn evenness; yarn flattening ratio; finite element analysis; image processing

10.13475/j.fzxb.20161004207

2016-10-17

2016-11-11

東華大學博士生創新基金項目(CUSF-DH-D-2015014)

李冠志 (1987—)，男，博士生。研究方向為紗線條干均勻度測試及布面質量預測。汪軍，通信作者，E-mail: junwang@dhu.edu.cn。

TS 101.9

A