高三學生數學解題元認知的調查研究

黃紅梅

（韓山師范學院數學與統計學院，廣東潮州521041）

高三學生數學解題元認知的調查研究

黃紅梅

（韓山師范學院數學與統計學院，廣東潮州521041）

高三學生的高考成績與數學解題元認知具有顯著的相關性，成績越好，數學解題元認知水平越高．不同學生群體數學解題元認知水平各異，理科生、男生、高成績組學生的數學解題元認知水平分別高于文科生、女生、低成績組學生，且對應二者具有顯著的差異，這些差異主要體現在元認知知識與元認知監控兩個主因素．

高三學生；數學；解題；元認知

1 引言

元認知首先由美國心理學家Flavell于1976年正式提出，他認為元認知是“個人關于自己的認知過程、結果或與其相關的知識”，以及“為完成某一具體的目標或任務，對認知過程進行主動的監測及連續的調節和協調”[1]．隨著研究的深入，研究者對元認知的界定逐漸形成了共識，即元認知是人們對認知活動的認識，實質是人們對認知活動的自我意識和自我調節，其結構成分包括元認知知識、元認知體驗、元認知調控[2]．元認知對認知的影響是多方面的，Swanson等人通過實證研究發現，元認知獨立于智力，可以彌補其它能力的不足[3]．董奇調查發現，元認知與思維品質存在顯著或非常顯著的正相關，這種聯系的實質是因果聯系[4]．在數學教育領域，元認知的研究主要集中在數學解題元認知方面．有學者認為，數學解題是一個認知與元認知交互作用與影響的過程，元認知深刻地影響數學解題[5]．另一些實證研究發現，元認知與數學成績具有相關性，即元認知水平越高，解題成績越好[6-8]．作為一個特殊的群體，高三學生的數學學習情況令人關注．本研究試圖從數學解題元認知新的視角，調查分析高三學生數學解題情況，以供參考．

2 研究方法與過程

2.1 被試對象

被試為剛開學報到的韓山師范學院的大學生，共215人，其中男47人，女168人，文科生44人，理科生171人．共發放問卷232份，回收215份，回收率92.6%．

2.2 測試資料

測試材料主要使用唐劍嵐編制的“數學問題解決中的元認知量表”[9]，該量表涵蓋了數學解題元認知結構的“三主因素九次因素”，即元認知知識（個體知識、認知任務、認知策略）、元認知體驗（情感體驗、認知體驗）、元認知策略（計劃、調控、評價、反思）．問卷信度與效度良好．

2.3 調查程序

主試先從學生信息系統中調取被試的高考數學成績，接著在新生報到期間向被試發放“數學問題解決中的元認知量表”問卷．

2.4 數據處理

使用統計工具SPSS 16.0對數據進行統計，考查高考成績與數學解題元認知的相關性，并通過獨立樣本檢驗分析文理科、高低成績組、不同性別的數學解題元認知的差異．

3 研究結果

3.1 高考成績與數學解題元認知的相關性

文理科高考成績與數學解題元認知及其各個主因素的相關系數如表1所示．由表中可以看出，文科成績、理科成績與數學解題元認知都存在著0.01水平上的顯著相關（r分別為0.60、0.42）．進一步從各主因素看，文科與理科成績與元認知知識、元認知監控均存在著0.01水平上的顯著相關（文科的相關系數r分別為0.61、0.57；理科的相關系數r分別為0.38、0.40），文科成績與元認知體驗相關性不顯著，而理科成績與元認知體驗則存在著0.05水平上的顯著相關（r為0.23）．

表1 文理科高考成績與數學解題元認知及其各個主因素的相關系數

3.2 文理科學生的數學解題元認知差異性

對文理科學生數學解題元認知及其各個主因素作t檢驗，得到如表2所示結果．數據顯示，在總水平上，理科生解題元認知平均分為115.41，高于文科生的106.52，且二者存在非常顯著的差異（t為-3.12）．在三大主要因素層面，理科學生在元認知知識、元認知監控的平均分均高于文科生，且都存在著非常顯著的差異（t分別為-4.86，-2.92）；而兩者的元認知體驗平均分相仿，沒有顯著性差異（t為0.40）．

表2 文理科學生的數學解題元認知及其各個主因素的差異性

進一步對文理科高考成績的數學解題元認知知識與元認知監控各個次因素作t檢驗，得到如表3所示結果．可以看出，對于元認知知識，文理科學生在個體知識、任務知識、策略知識上都具有非常顯著的差異（t分別為-2.64，-4.03，-3.94）；對于元認知監控，文理科學生在調控策略上存在非常顯著的差異（t為-3.25），而在其它三個次因素計劃策略、評價策略、反思策略上則存在顯著差異（t分別為-2.54，-2.29，-2.04）．

表3 文理科學生的數學解題元認知及其各個次因素的差異性

3.3 不同性別學生的數學解題元認知差異性

對不同性別學生的數學解題元認知及其各個主因素作t檢驗，得到如表4所示結果．數據顯示，在總水平上，男生數學解題元認知平均分為119.98，高于女生的111.80，且二者存在非常顯著的差異（t為-2.93）．在三大主要因素層面，男生在元認知知識、元認知監控上的平均分均高于女生，且在元認知知識上存在顯著的差異（t為-2.54），在元認知監控上存在非常顯著的差異（t為-3.56），而男女生在元認知體驗上平均分接近，不存在差異性．

表4 不同性別學生的數學解題元認知及其各個主因素的差異性

進一步對不同性別學生的數學解題元認知知識與元認知監控各個次因素作t檢驗，得到如表5所示結果．可以看出，男女生在元認知知識的策略知識上存在顯著性差異（t為-2.34），在元認知監控的兩個次因素評價策略、反思策略上存在非常顯著的差異（t分別為-3.72，-3.87），而在其它各個次因素中不存在差異性．

表5 不同性別學生的數學解題元認知及其各個次因素的差異性

3.4 高低成績組學生的數學解題元認知差異性

3.4.1 文科高低成績組學生的數學解題元認知差異性

對文科高低成績組學生的數學解題元認知及其各個主因素作t檢驗，得到如表6所示結果．數據顯示，在總水平上，高成績組學生數學解題元認知平均分為125.17，遠高于低成績組學生的90.50，且二者存在非常顯著的差異（t為-5.05）．在三大主要因素層面，高成績組學生在元認知知識、元認知監控上的平均分均高于低成績組學生，且二者在這兩個主要因素上均存在非常顯著的差異（t分別為-7.35，-3.83）．而高低成績組學生在元認知體驗上平均分接近，不存在差異性.

表6 文科高低成績組學生的數學解題元認知及其各個主因素的差異性

進一步對文科高低成績組學生的數學解題元認知各個次因素作t檢驗，得到如表7所示結果．可以看出，高低成績組學生在元認知知識的個體知識、任務知識、策略知識三個次因素以及元認知監控的調控策略、反思策略兩個次因素上均存在顯著性差異（t分別為-2.66，-2.99，-3.03，-2.51，-3.09），在元認知監控的另兩個次因素計劃策略、評價策略上則存在非常顯著的差異（t分別為-3.75，-3.23）．而在元認知體驗的兩個次因素上均不存在差異性．

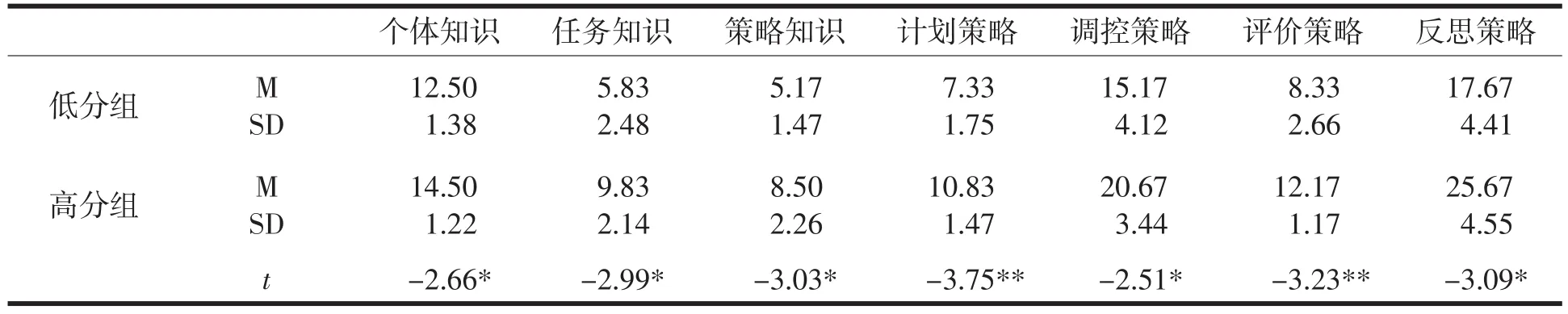
表7 文科高低成績組學生的數學解題元認知及其各個次因素的差異性

3.4.2 理科高低成績組學生的數學解題元認知差異性

對理科高低成績組學生的數學解題元認知及其各個主因素作t檢驗，得到如表8所示結果．數據顯示，在總水平上，高成績組學生數學解題元認知平均分為124.96，遠高于低成績組學生的105.67，且二者存在非常顯著的差異（t為-4.64）．在三大主要因素層面，高成績組學生對應平均分均高于低成績組學生，且二者在元認知知識以及元認知監控這兩個主要因素上均存在非常顯著的差異（t分別為-2.96，-4.99），而在元認知體驗上則不存在差異性．

表8 理科高低成績組學生的數學解題元認知及其各個主因素的差異性

進一步對理科高低成績組學生的數學解題元認知知識與元認知監控各個次因素作t檢驗，得到如表9所示結果．可以看出，高低成績組學生在元認知知識的任務知識、策略知識兩個次因素以及元認知監控的計劃策略、調控策略、評價策略、反思策略四個次因素上均存在非常顯著性差異（t分別為-2.76，-3.34，-3.83，-3.24，-5.26，-3.76）．

表9 理科高低成績組學生的數學解題元認知及其各個次因素的差異性

4 結論與建議

4.1 研究結論

（1）文理科高考成績與數學解題元認知均具有顯著的相關性．對文科而言，這種顯著的相關性主要表現在元認知知識、元認知監控兩個主因素；對理科而言，則在元認知知識、元認知體驗以及元認知監控三個主因素上都有所體現．

（2）理科生解題元認知水平高于文科生，且二者存在顯著差異，這種差異主要表現在元認知知識、元認知監控兩個主因素，以及它們所有的次因素．

（3）男生數學解題元認知水平高于女生，且二者存在顯著差異，這種差異主要表現在元認知知識、元認知監控兩個主因素，以及它們對應的策略知識、評價策略、反思策略三個次因素．

（4）不論是文科生還是理科生，高成績組學生數學解題元認知水平均高于低成績組學生，且二者存在顯著的差異，這種差異主要表現在元認知知識、元認知監控兩個主因素，以及它們對應的所有次因素（理科生則除個體知識外）．

總體看，一方面，高三學生的高考成績與數學解題元認知具有較強的相關性，元認知水平越高，高考成績越好，反之亦然．另一方面，高三學生數學解題元認知狀況不容樂觀，這尤其表現在女生、文科生以及數學學困生三類人群，這些學生的元認知知識、元認知監控兩個主因素及其對應的次因素層面明顯偏低．

4.2 教學建議

高三學生數學解題元認知狀況令人擔憂，提升高三學生（甚至是整個高中階段學生）的數學解題元認知水平已迫在眉睫，需要一線教師給予足夠的重視，并采取具有針對性的訓練措施．實驗表明，以下元認知訓練方式可以顯著提升學生數學元認知能力，值得借鑒．

（1）解題元認知提示語策略[10]，教師依據《波利亞怎樣解題表》編制一個簡便的解題“自我提問”訓練單，教師在教學中示范性使用訓練單，并要求學生在解題中靈活運用訓練單來監控與調節整個解題過程．

（2）相互講題策略[11]，要求講題人講解時需要說明選擇哪種方法，并講清楚先做什么，后做什么，再做什么，最后還要說出解決這個問題易犯的錯誤和解決這個問題的關鍵．

（3）題后反思策略[11]，要求學生反思數學解題過程．譬如，自己是怎樣發現和解決問題的？運用了哪些數學思想方法？解題時你走過哪些彎路？解題時容易犯什么樣的錯誤？從中可以吸取什么樣的教訓？還有其它哪些方法？

（4）數學作文[12]，要求學生對作業及考試中的錯題原因做出書面分析，寫成反思性的作文，并且不能簡單地歸因于不認真、馬虎、粗心等原因，而要從審題、知識掌握、計算程序及選用的方法等方面進行細致分析，每周交反思性作文一次．

值得注意的是，數學元認知訓練方式有別于常規的數學題海訓練，它主要通過針對性的訓練提高學生元認知水平，進而間接提高學生數學解題能力．在日常的數學教學中，數學元認知訓練可以作為一種輔助手段，幫促學生養成良好的解題習慣，進而提高解題能力．

參考文獻：

[1]Flavell J H.Cognitive Development：Children’s Knowledge about the Mind[J]．Annual Review of Psychology，1999，50（1）：21-44．

[2]歐慧謀，唐劍嵐．國內數學元認知的研究與思考[J]．課程·教材·教法，2015，32（5）：58-61．

[3]Swanson H L.Influence of metacognitive knowledge and aptitude on problem solving[J]．Journal of Educational Psychology，1990，82（2）：306-314．

[4]董奇．元認知與思維品質關系性質的相關實驗研究[J]．北京師范大學學報（哲學版），1990（5）：51-58．

[5]Artzt A，Armour Thomas E．Development of a Cognitive-metacognitive Framework for Protocol Analysis of Mathematical Problem Solving in Small Groups[J]．Cognition and Instruction，1992，9（2）：137-175．

[6]周瑩，唐劍嵐．高師大二學生數學解題的元認知對解題成績的影響[J]．數學教育學報，2007，16（2）：60-63．

[7]湯服成，郭海燕，唐劍嵐．初一學生數學問題解決中的動靜態元認知研究[J]．數學教育學報，2005，14（1）：59-62．

[8]熊春連，王延文，王光明．數學優秀生的學習心理特征[J]．數學教育學報，2009，18（2）：42-45．

[9]唐劍嵐，周瑩，湯服成．數學問題解決中的元認知問卷量表的設計[J]．數學教育學報，2005，14（4）：44-47．

[10]黃紅梅．數學問題解決元認知能力的培養——基于波利亞解題元認知思想[D]．桂林：廣西師范大學，2015．

[11]連四清，郭海杰．中學數學學困生題后反思的元認知技能培訓[J]．數學教育學報，2005，14（2）：56-58．

[12]劉婷，羅增儒．“數學作文與元認知開發”的糾錯實驗[J]．數學教育學報，2009，18（4）：50-51．

An Investigation into Students’Meta-Cognition of Problem-Solving in Senior Grade Three Mathematics

HUANG Hong-mei
（College of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong,521041）

The score of the university entrance examination of senior grade three has remarkable correlation with students’meta-cognition of mathematical problem-solving.The higher the score,the better the meta-cognition of mathematical problem-solving.The level of mathematical problem-solving meta-cognition is diverse among different student groups.The level of science students,boys and high achievers are respectively higher than arts students,girls and low achievers.Moreover,they have significant difference respectively in terms of the two following factors:meta-cognitive knowledge and meta-cognitive monitoring.

senior grade three;mathematics;problem solving;meta-cognition

G 623.5

A

1007-6883（2017）03-0083-06

責任編輯周春娟

2017-01-06

黃紅梅（1983-），女，湖南郴州人，韓山師范學院數學與統計學院助教.