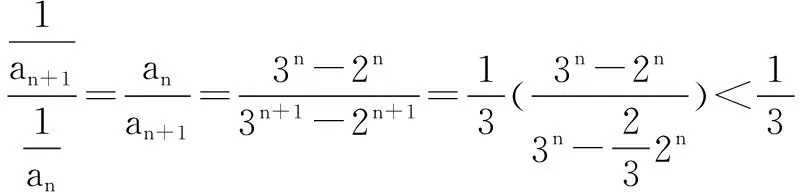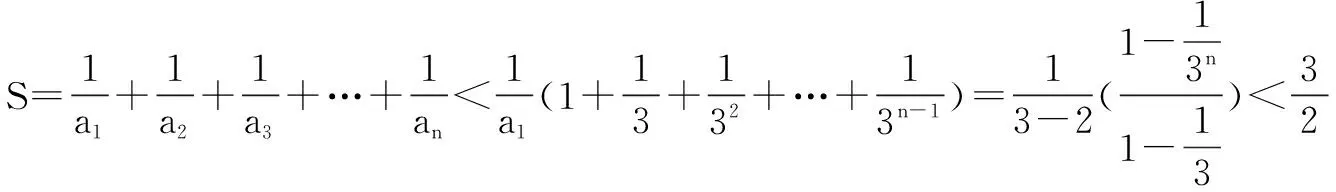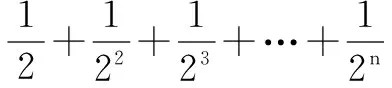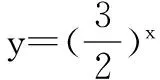淺談高中數學概念研究的幾點認識
戴天竹
(江蘇省蘇州實驗中學,江蘇 蘇州 215000)
?
淺談高中數學概念研究的幾點認識
戴天竹
(江蘇省蘇州實驗中學,江蘇 蘇州 215000)
本文以導數的概念、數列求和的引入為例,從多角度闡述了研究概念的重要性以及研究概念的常用方法.
定義;概念;導數;導數的定義;數列求和;放縮法
著名數學家華羅庚教授在“大哉數學之為用”一文中精采地敘述了數學的各種應用:宇宙之大,粒子之微,火箭之速,化工之巧,地球之變,生物之謎,日用之繁等各個方面,無處不有數學的重要貢獻.他指出:數學是一切科學得力的助手和工具.它有時由于其它科學的促進而發展,有時也先走一步,領先發展,然后再獲得應用.任何一門科學缺少了數學這一工具便不能確切地刻劃出客觀事物變化的狀態,更不能從已知數據推出未知的數據來,因而就減少了科學預見的可能性,或者減弱了科學預見的精確度.數學的重要地位也帶來了數學這門學科在高中教育中的重要地位.現今,高考數學對基礎概念,基礎技能更加重視,這也提示我們:高中數學教學中對概念深入研究是重要的.
從多角度把握概念的含義對我們解決數學問題有舉足輕重的作用.本文就從多角度把握概念含義來談談高中數學概念的研究.
一、“數”的角度
“數形結合”是一個很重要的數學思想方法.我們就先從“數”的角度來研究,這里以導數的定義來舉例.
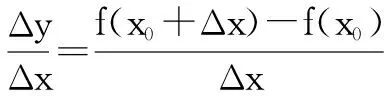

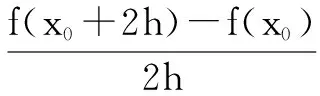
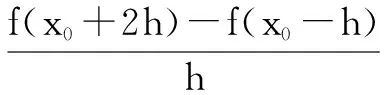
解:我們先將所求式子變形(向導數定義中式子靠攏),有

二、“形”的角度

這里我們也以導數為例.導數f′(x0)的幾何意義就是曲線y=f(x)在點P0(x0,f(x0))處的切線的斜率.
我們都知道切線可以用直線逼近的方法得到:設P是曲線上不同于P0的一點,隨著點P沿曲線向點P0運動,割線PP0在點P0附近越來越逼近曲線在點P0處的切線.當點P無限逼近點P0時,直線PP0最終成為曲線在點P0處的切線.
如右圖所示曲線,此類曲線與點P0處的切線之間還有些特殊的關系,比如將切線向上平移后與曲線有2個交點,再比如在點P0附近(除點P0外)曲線都在其切線上方.對于這類凹(凸)函數,事實上在切點附近都有類似的性質,這些相關特點在我們的解題中也有相當幫助.

解 首先,我們得到函數的定義域為[0,2],題目中要求將函數圖象繞坐標原點逆時針旋轉θ,我們可以考慮將坐標軸繞坐標原點順時針旋轉θ,旋轉后的圖象與x軸垂直的直線至多有1個交點.原函數的圖象如右圖所示,坐標軸旋轉后如果y軸與函數在x=x0∈(0,2)處的切線平行,則y軸與函數圖象必定還有除原點外的另一個交點,即坐標軸旋轉后使得y軸與函數在x=0處的切線平行是極限位置,下面求函數在x=0處的切線斜率即可.

例3 已知函數f(x)的定義域為R,f(2)=3,且f(x)在R上的導函數滿足f′(x)-1<0,解不等式f(x2) 探究概念的本質內涵,能給我們解題帶來相應的思路,從定義出發,從基礎概念出發往往能事半功倍,課本上定義是如此,有時課本上一些概念的引入(尤其是一些經典的引入),更能給我們以啟發. 故原不等式得證. [1]戴榮. 對高中數學概念教學的幾點認識與思考[J]. 新課程導學,2013(35):19. [2]王韶君. 淺談高中數學新課標理念的幾點認識[J]. 中學教研(數學),2007(05):4-6. [責任編輯:楊惠民] 2017-05-01 戴天竹(1982.11-),男,漢,一級,碩士,從事組合數學教學. G632 B 1008-0333(2017)16-0006-02

三、從“引入”出發