一道競賽題的多種證法
2017-07-21 09:32:29張卜
數理化解題研究 2017年16期
張 卜
(陜西省西安市周至縣第二中學,陜西 西安 710400)
?
一道競賽題的多種證法
張 卜
(陜西省西安市周至縣第二中學,陜西 西安 710400)
通過對1963年莫斯科數學競賽中一道經典不等式的研究,探究出它的多種證法.
不等式;證明;競賽題
題目 設a,b,c∈R+求證:

這是1963年莫斯科數學競賽中的一道題,考查的是不等式最值問題,其靈活性強、難度大.筆者從不同角度來探究該題的證法.
證明1 柯西不等式法
證明2 排序不等式法
由對稱性,這里不妨設a≥b≥c>0,
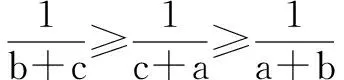
再由排序不等式知,順序和≥亂序和,


證明3 換元法
令x=b+c,y=c+a,z=a+b,可求解出



證明4 均值不等式法

證明5 構造函數法


證明6 放縮法
由上式左端可以看出,三個分式的分子之和等于0,所以,在不增大各個分數值的前提下,可將它們的分母變為相等. 這里假設a≥b≥c,則有a≥1,c≤1.


(Ⅱ)若a≥1≥b≥c,則將上述不等式左端的三個分式的分母換為3-b,即保證其中一個負分數值不變,另一個負分數值只可能減小,正分數值不增大,可得

證明7 向量法


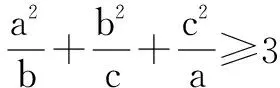

以上三式相加即證.
證明8 切線法

不等式等號成立的條件是a=b=c=1,
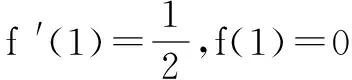


以上三式相加即證.
通過對一道競賽題的多視角分析,開拓和啟發解題思維能力和發散思維能力.根據不同的問題角度,逐一給出數學思想方法,不斷地優化數學思維能力,使知識和方法融化貫通,提高自身的分析問題能力和解決問題的能力.
[1]許波.一道不等式證明題的多種解法[J].中等職業教育(理論),2008(4).
[責任編輯:楊惠民]
2017-05-01
張卜(1987.4-),陜西省西安市高陵區,碩士,中學二級,從事高中數學教學.
G632
B
1008-0333(2017)16-0011-02
猜你喜歡
意林(兒童繪本)(2020年2期)2021-01-07 02:12:06
意林(兒童繪本)(2019年12期)2020-01-04 02:09:58
意林(兒童繪本)(2019年10期)2019-12-23 09:03:36
意林(兒童繪本)(2019年6期)2019-08-05 01:22:04
學苑創造·A版(2019年5期)2019-06-17 01:14:21
兒童繪本(2018年19期)2018-10-31 21:02:34
兒童繪本(2018年9期)2018-06-04 16:40:12
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

