求最值的常用方法
——以一道高考題為例
羅 燕
(陜西省延安市吳起高級(jí)中學(xué),陜西 延安 717600)
?
求最值的常用方法
——以一道高考題為例
羅 燕
(陜西省延安市吳起高級(jí)中學(xué),陜西 延安 717600)
最值問題是一種能力考查題,它能有效地考查學(xué)生對(duì)知識(shí)和方法的綜合與靈活應(yīng)用.因此,求解最值問題,是高考數(shù)學(xué)中的熱點(diǎn),也是學(xué)生平時(shí)學(xué)習(xí)的難點(diǎn).本文通過對(duì)一道高考題的研究,歸納了幾種高考中常用的求最值的方法.
最值;方法;高考題
最值問題是高中數(shù)學(xué)的重要內(nèi)容之一,也是高考的熱點(diǎn)問題.它可以以求最值為載體,考查高中數(shù)學(xué)的主要知識(shí)與方法,解決最值問題要求學(xué)生要有扎實(shí)的數(shù)學(xué)基本功與良好的數(shù)學(xué)思維能力.本文試以2016年江蘇高考數(shù)學(xué)試卷中的14題為例,探析最值問題在高考中的常見解決方法.
題目:在銳角三角形ABC中,若sinA=2sinBsinC,則tanAtanBtanC的最小值是____.
解法一 構(gòu)造二次函數(shù)求最值
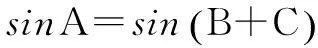
∴sinBcosC+cosBsinC=2sinBsinC,
∴tanB+tanC=2tanBtanC.
又∵tanA+tanB+tanC=tanAtanBtanC,
∴tanA+2tanBtanC=tanAtanBtanC,
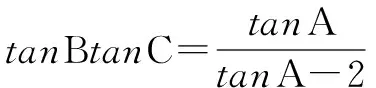
又tanBtanC>0,
∴tanA>2.
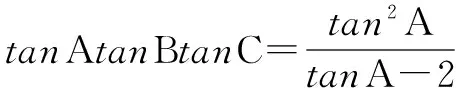
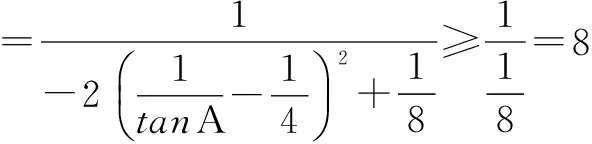
所以tanAtanBtanC的最小值是8.
點(diǎn)評(píng) 設(shè)法構(gòu)造二次函數(shù),利用二次函數(shù)的解析式及性質(zhì)獲得最大(小)值.
解法二 利用均值不等式求最小值
前面化解步驟同解法一,
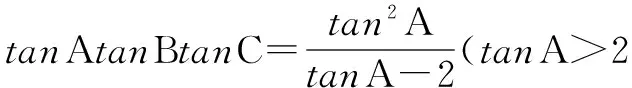

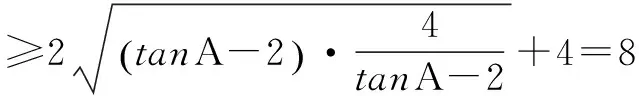
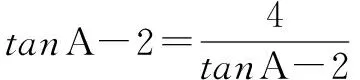
所以tanAtanBtanC的最小值是8.
點(diǎn)評(píng) 利用均值不等式求最值時(shí),要注意“一正,二定,三相等”;構(gòu)造“定值”,口訣是“和定積最大,積定和最小”.
解法三 利用函數(shù)單調(diào)性求最小值
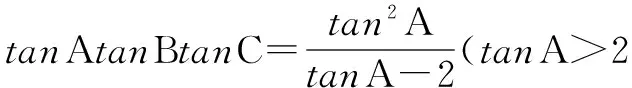
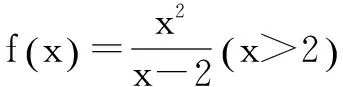


點(diǎn)評(píng) 利用函數(shù)的單調(diào)性求最值,需要先判斷函數(shù)在給定區(qū)間上的單調(diào)性,然后結(jié)合單調(diào)性求最值
解法四 利用方程思想求最小值
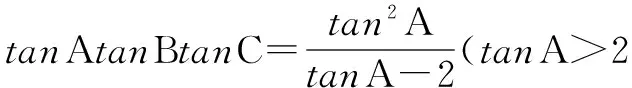
設(shè)t=tanAtanBtanC,x=tanA,
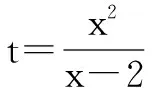
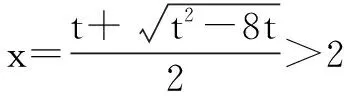



解得t≥8.
所以tanAtanBtanC的最小值是8.
方法 利用方程根的取值情況,列不等式組,然后求函數(shù)的最值.
當(dāng)然,解最值問題的方法遠(yuǎn)不止這些,比如,還有三角代換法、放縮法、反函數(shù)法等等,這里僅是根據(jù)這道高考題列舉了求最值問題的幾種方法.另外,通過不同方法的求解,也體現(xiàn)出高考題的綜合性.在平時(shí)的學(xué)習(xí)中,只要我們能夠熟練地掌握各種方法,就能在高考場(chǎng)上游刃有余.
[1]代歡.高中數(shù)學(xué)函數(shù)最值問題的幾種求解方法[J].理科考試研究,2017(01).
[2]王超.三角函數(shù)最值問題探究[J].理科考試研究,2014(07).
[責(zé)任編輯:楊惠民]
2017-05-01
羅燕(1985.7-),女,四川,中學(xué)二級(jí)教師,研究生,從事數(shù)學(xué)教育.
G632
B
1008-0333(2017)16-0019-02

