自適應二階雙穩態隨機共振的微弱特征增強檢測方法研究

羅 毅

（貴陽學院機械工程學院，貴州 貴陽 550005）

自適應二階雙穩態隨機共振的微弱特征增強檢測方法研究

羅 毅

（貴陽學院機械工程學院，貴州 貴陽 550005）

針對大型機械設備運行環境惡劣故障特征難以提取的問題，提出一種自適應二階雙穩態隨機共振方法。首先系統輸出信號的信噪比作為蟻群算法的自適應度函數，然后采用蟻群算法優化二階隨機共振系統的參數和阻尼因子，再利用優化得到的最佳參數設置二階隨機共振系統，最后實現微弱故障特征的增強與提取。數值仿真分析表明：該方法可以有效地提取淹沒在強噪聲背景下的微弱正弦信號；而且深溝球軸承滾動體故障實驗結果證明提出的方法能有效增強與提取滾動體故障特征頻率。仿真與實驗對比結果表明：提出的方法優于傳統隨機共振方法，歸功于該方法不僅能夠利用蟻群算法并行選擇和優化隨機共振系統參數，而且克服傳統隨機共振方法對高通濾波器的依賴。

二階雙穩態隨機共振；蟻群算法；微弱特征檢測；故障診斷

0 引 言

大型機械設備通常運行在低速重載等惡劣工況下，由于復雜多變的振動傳遞路徑以及工況的強背景噪聲，導致獲取的信號不僅復雜多變，且信噪比極低。因此，微弱特征提取一直是大型機械設備故障診斷中的關鍵難題。而早期故障更加微弱，實現早期故障特征提取更具挑戰。

隨機共振被Benzi等[1]提出，能利用噪聲增強微弱特征，已被廣泛應用于故障診斷[2-4]領域。例如：焦尚彬等[5]應用一階雙穩態隨機共振，實現了多頻微弱特征的提取，但是需依賴于高通濾波器濾除低頻干擾，而且人為選擇濾波器參數易造成誤檢，甚至增強效果不佳；潘崢嶸等[3]提出符號序列熵指標衡量一階雙穩態隨機共振系統的輸出，實現了軸承微弱早期故障特征的提取；Lei等[6]提出一階雙穩態隨機共振方法，利用高通濾波器抑制低頻噪聲，實現了行星齒輪箱的故障診斷，可以看出濾波器參數設置需要人為經驗知識，否則可能導致系統輸出發散；Qiao等[7]提出一階非飽和隨機共振方法實現了軸承和齒輪箱的故障診斷，該方法克服了傳統一階隨機共振的內在飽和問題，提升了隨機共振的增強能力；Lu等[8]提出全波增強隨機共振新方法，實現了旋轉機械的故障診斷。該方法主要克服了機械振動信號包絡誘導粒子躍遷的缺點，構造全波信號更好地誘導隨機共振的發生，從而實現微弱特征的增強與提取；Matthew等[9]基于隨機共振實現了微弱正弦信號的提取，該方法利用兩個子系統之間的耦合機制改善了隨機共振的增強能力；Rebolledo等[10]研究了二階隨機共振的微弱信號增強方法，結果表明二階隨機共振系統的增強能力優于傳統一階隨機共振系統，為二階隨機共振在微弱信號提取中的應用奠定了理論基礎。

綜上所述，已有隨機共振方法主要聚焦在一階隨機共的應用上，它易遭受低頻噪聲干擾，需依賴于高通濾波器的輔助，濾波器參數設置不合理可能導致微弱特征增強效果不佳，甚至誤檢。為了克服以上缺點，改善隨機共振的微弱特征增強能力，提出了自適應二階雙穩態隨機共振方法。與已有方法相比，該方法不僅能利用蟻群算法自適應地選擇和優化隨機共振系統的多個參數，而且能夠抑制低頻噪聲干擾，從而消除對濾波器的依賴，克服了濾波器參數選擇的困擾。

1 傳統一階雙穩態隨機共振方法

受隨機噪聲和周期外力激勵的布朗粒子在一階雙穩態勢阱中的運動可以由郎之萬方程[7-8]描述為

式中：A、Ω——微弱周期信號的幅值和角頻率；

η（t）——高斯白噪聲。

η（t）滿足以下條件：

式中D是噪聲強度。

U（x）是雙穩態勢函數，其表達式如下：

式中a和b是系統參數，且均大于0。

不同系統參數下的雙穩態勢函數及相應的回復力如圖1所示，從圖1（a）可以看出勢函數在處有兩個極小值點，在x=0處有一個極大值點，其勢壘高度為ΔU=a2/（4b）。當不存在任何外力的情況下，對應的回復力如圖1（b）所示，可以發現當布朗粒子運動到左側勢阱時，勢函數本身會產生一個反方向回復力 F（x）=-dU（x）/dx驅使粒子向右側勢阱運動，反之亦然。從而雙穩態勢函數具備了粒子阱間躍遷的可能，能夠承載隨機共振的發生。此外，可以看出，通過調節系統參數可以有效控制布朗粒子的運動，進而實現機械振動信號中微弱特征的增強與提取。隨機共振受絕熱近似條件的限制，只能檢測小頻率信號，然而機械故障信號通常是頻帶較寬的大頻率信號，為了實現大頻率特征信號的有效提取，尺度變換被廣泛應用到早期故障微弱特征提取中。

圖2給出了傳統一階雙穩態隨機共振檢測早期故障微弱特征的基本原理框圖，可以看出獲取的帶噪機械振動信號必須經過高通濾波器預處理，才能送入隨機共振系統。

如圖1（a）所示，通過調節系統參數a和b能夠有效控制勢函數的壘高和勢阱的寬度，從而控制布朗粒子的運動速率實現微弱特征的增強與提取。但是，已有方法人為主觀地選擇參數a和b，忽略了參數之間的協同效應，從而導致微弱特征檢測能力受限。顯然，傳統一階隨機共振方法不僅人為主觀地選擇系統參數，忽略了參數之間的協同作用，而且其基于的一階模型易遭受低頻噪聲干擾，需依賴于高通濾波器的輔助，濾波器參數設置不合理可能導致微弱特征增強效果不佳，這兩個缺點已經限制了隨機共振的微弱特征增強與提取能力。

2 自適應二階雙穩態隨機共振早期故障微弱特征檢測方法

一方面，傳統一階雙穩態隨機共振方法易遭受低頻噪聲的干擾，需依賴于高通濾波器的輔助處理，而且濾波器參數設置依賴于人為選取，選擇不合理易導致微弱信號增強效果不佳。另一方面，傳統一階雙穩態隨機共振方法人為主觀地選擇系統參數，忽略了參數之間的協同作用，從而導致系統輸出信號不是最佳共振輸出，沒有充分發揮隨機共振早期故障微弱特征的增強能力。為了克服以上兩個缺點，提出了自適應二階雙穩態隨機共振早期故障微弱特征增強檢測方法。二階雙穩態隨機共振系統由朗之萬方程[10]描述為

圖1 不同系統參數下的雙穩態勢函數及其回復力

圖2 傳統一階雙穩態隨機共振早期故障微弱特征檢測方法的原理框圖

式中x是系統響應，其本質是布朗粒子在隨機力η（t）和周期外力AcosΩt激勵下，在勢函數U（x）中的運動軌跡；β∈[0，1]是阻尼因子。

提出的自適應二階雙穩態隨機共振新方法采用基于網格劃分的蟻群算法同時優化二階隨機共振系統參數a，b和β，其中蟻群大小、網格分割段數、初始信息素濃度、最大進化代數Gmax等主要參數的設置參考文獻[11]。選擇二階雙穩態隨機共振系統輸出信號的信噪比作為蟻群算法適應度函數。信噪比大小反映了處理后信號的優劣程度，信噪比越大說明系統輸出信號中噪聲越小，故障特征越明顯，信噪比越小則不利于早期故障特征的提取和診斷。因此，信噪比能定量反映二階雙穩態隨機共振系統輸出信號的優劣程度，利于微弱特征的提取。利用蟻群算法的自適應二階雙穩態隨機共振早期故障微弱特征增強與提取方法的流程如圖3所示。

圖3 提出的自適應二階雙穩態隨機共振早期故障微弱特征提取方法流程圖

具體步驟如下：

1）對獲取的帶噪滾動軸承振動信號進行預處理。由于軸承故障特征通常受轉速信息的調制，因此，希爾伯特變換被用于解調故障信號，求取相應的包絡信號。然后，采用尺度變換壓縮求得的包絡信號，使其滿足隨機共振的小參數輸入條件。

2）劃分搜索網格并隨機在搜索網格節點處放置覓食螞蟻，每個搜索節點對應一組二階雙穩態隨機共振系統參數（a，b，β）。

3）依據每個搜索節點的信息素濃度得到相應的概率值，并根據概率值的大小隨機地移動覓食螞蟻到下一個目標節點，該過程即為初始化蟻群算法優化的參數對（a，b，β）。

4）依據適應度函數，即隨機共振系統輸出信噪比，來優化、更新信息素濃度，從而計算最新的概率值，并根據概率值判斷搜索網格每列上覓食螞蟻所選節點是否收斂。若收斂，則找出各列中概率值最高的網格節點，否則跳至步驟3），繼續搜索最佳網格節點；若最佳網格節點處的適應度函數值大于公告板記錄，則更新公告板，始終使公告板記錄最佳參數對和對應的最大輸出信噪比值。在這里，適應度函數被定義為二階雙穩態隨機共振系統輸出信號的信噪比，其具體表達式如下：

式中：Ad——二階雙穩態隨機共振系統輸出信號特征頻率的幅值；

Ai——輸出信號頻譜中每根譜線的幅值；

N——系統輸入尺度變換后包絡信號的長度。

5）在收斂的網格節點處進行更小的區間劃分，然后轉到步驟2），不斷搜索最佳網格節點，直至進化代數達到預設的最大進化代數Gmax，則輸出最佳網格節點，該節點對應的參數對（a，b，β）best即為求得的二階雙穩態隨機共振系統最優參數對。

6）將最優參數對（a，b，β）best代入二階雙穩態隨機共振系統形成最后的優化系統，并將尺度變換后的軸承故障包絡信號輸入該優化系統，利用四階龍庫塔算法求解該二階雙穩態隨機共振系統的輸出信號，對該輸出信號進行傅里葉變換提取微弱特征，并實現滾動軸承的早期故障診斷。

3 仿真分析

為了驗證提出方法的有效性，一個頻率50 Hz、幅值0.05的余弦信號和強度為4的高斯白噪聲混合，得到的待檢混合信號的時域波形和頻譜分別如圖 4（a）和圖 4（b）所示。 采樣頻率為 12.8kHz，采樣時間為1s。從圖4（a）可以看出，余弦信號完全被噪聲所淹沒，很難看出周期性的波形，在頻譜圖4（b）中，特征頻率50 Hz完全被噪聲所淹沒，難以辨別。同時，根據式（10）計算得到混合信號的信噪比為-38.9564dB，可見信噪比極低。

首先，傳統一階雙穩態隨機共振方法如圖2所示，被用于處理圖4的待檢混合信號，設置高通濾波器的通帶截止頻率和阻帶截止頻率分別為36Hz和45Hz，頻移尺度變換的頻移因子為36，尺度因子為200，壓縮后的特征頻率為（50-36）/200=0.07＜＜1Hz，滿足絕熱近似下的小參數限制。得到的最佳增強與提取結果如圖5所示，可以看出特征頻率50Hz在整個頻譜中被突出，而且時域特征具有明顯的余弦周期波形。但是，在時域波形和頻譜中仍然具有很強的噪聲干擾，而且還有濾波器的干擾頻率36 Hz，那是因為在高通濾波器輔助處理過程中，濾波器參數人為設置不合理導致系統輸出信號中存在明顯的濾波器通帶截止頻率的干擾。此外，在特征頻率50Hz周圍有很強的噪聲頻率，導致很難判斷是否有故障發生，這是因為人為主觀選擇系統參數進一步造成隨機共振增強能力下降所致。因此，現有的隨機共振方法很難檢測低信噪比環境的微弱特征，為了定量描述增強結果，計算得到隨機共振系統輸出信號特征頻率的幅值和信噪比分別是0.1644dB和-19.9722dB。

圖4 待檢混合信號

顯然，傳統的一階隨機共振方法增強與提取結果并不令人滿意。于是，圖6給出了提出方法的檢測結果，可以看出噪聲基本被消除，時域波形具有明顯的余弦波特點，而且頻譜中特征頻率50Hz完全在整個頻譜中處于主導地位，干擾頻率幅值非常微弱。輸出信號特征頻率的幅值和信噪比分別為0.223 8 dB和-11.8559dB。對比兩種方法的增強結果，提出的方法不僅獲得了最大的特征頻率幅值，而且也獲得了較高的輸出信噪比。這一結果歸功于二階雙穩態隨機共振的非線性帶通濾波器特性，它不僅能夠抑制低頻噪聲干擾，而且能夠將高頻噪聲向低頻壓縮實現微弱信號的增強，從而不依賴于高通濾波器的輔助處理。此外，提出方法令人滿意的增強與提取結果也歸功于蟻群算法對系統參數的優化，考慮了系統參數之間的協同作用，從而最大化地實現了早期故障微弱特征的增強與提取。仿真結果證明了提出方法的有效性。

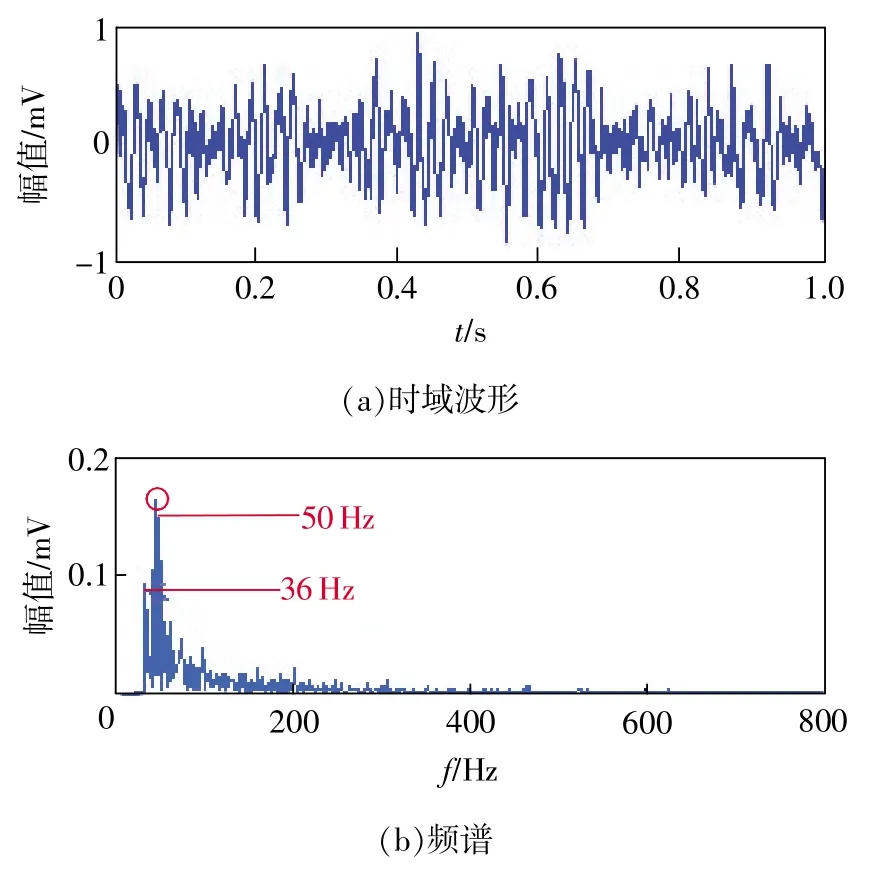
圖5 傳統一階雙穩態隨機共振方法的增強提取結果

圖6 提出方法的增強提取結果

為了進一步分析提出方法的反噪聲能力，固定正弦信號的特征頻率為50Hz，觀察隨噪聲強度變化時，兩種方法的輸出信噪比，如圖7所示。可以看出，隨著噪聲強度的增加，輸入信號信噪比逐漸下降，它是合理的。而提出方法的輸出信噪比曲線總在傳統方法之上，說明提出方法具有更好的反噪聲能力，適合更低信噪比環境的微弱特征檢測。這一結果歸功于提出方法不僅考慮了系統參數之間的協同作用，而且能抑制低頻噪聲，克服了對高通濾波器的依賴。

4 實驗驗證

滾動軸承作為重要的機械旋轉部件之一，其故障信號表現出典型的微弱沖擊特征，且通常被強烈的背景噪聲所淹沒，難以檢測和提取，尤其是滾動體故障。于是，凱斯西儲大學的滾動軸承實驗數據被采用驗證提出方法的實際應用價值，其軸承型號是6205-2RS JEM SKF深溝球軸承，主要參數可以參考文獻[12]，采樣頻率為48 kHz，采樣時間為1 s，軸承轉速為1750r/min。計算滾動體的理論故障特征頻率為froller=137.5 Hz。滾動體故障振動信號的時域波形和頻譜如圖8所示，可以看出在圖8（a）中時域波形被強噪聲所淹沒，很難發現周期性沖擊，而在圖8（c）的包絡譜中可以看到微弱的滾動體故障頻率froller，但是在整個頻譜中顯得極其微弱，難以判定是否發生早期故障，若判定無故障，可能導致漏診，甚至造成重大事故。

圖7 提出方法與傳統方法的反噪聲能力對比

首先，利用傳統一階雙穩態隨機共振方法處理圖8的滾動體故障信號，其隨機共振系統輸出信號的時域波形和頻譜分別如圖9（a）和圖9（b）所示。可以看出，頻譜中有明顯的滾動體故障頻率137.5Hz，而且其在整個頻譜中占主導地位。但是，在滾動體故障頻率附近存在較強的噪聲干擾頻率，從而導致很難直接斷定故障的發生。為了更加準確地判斷故障的發生，提出的自適應二階雙穩態隨機共振方法被利用處理圖8的滾動體故障信號，其增強結果的時域波形和頻譜分別如圖10（a）和圖10（b）所示。從頻譜圖可以看出，滾動體故障頻率在整個頻譜中被突出，而且周圍的干擾頻率較小。因此，能準確推斷出軸承的滾動體發生了早期故障，應該進行及時維修，從而避免事故的發生。對比圖9和圖10，不難發現提出的方法不僅能夠最大程度地增強早期故障的微弱特征，而且能夠抑制不同尺度的噪聲，從而消除噪聲頻率的干擾，使得診斷結果更加準確可信。軸承故障實驗證明了提出方法的可行性和優越性。

圖8 滾動體故障信號

5 結束語

圖9 傳統一階雙穩態隨機共振方法增強提取結果

圖10 提出的自適應二階雙穩態隨機共振方法增強提取結果

隨著機械設備朝著高精尖發展，其工作環境也越來越惡劣，導致獲取的信號不僅復雜多變，且信噪比極低。傳統基于一階模型的雙穩態隨機共振方法不僅人為主觀選擇系統參數，忽略了參數之間的協同效應，而且易遭受低頻噪聲的干擾，需依賴于高通濾波器的輔助處理，若高通濾波器參數設置不合理可能導致增強結果中存在來自濾波器本身的干擾。為了解決以上問題，提出了自適應二階雙穩態隨機共振方法，該方法利用蟻群算法自適應的優化系統參數，實現了參數之間的協同作用，而且二階隨機共振能夠抑制多尺度噪聲，不需依賴于高通濾波器的輔助處理，從而能夠實現早期故障的微弱特征增強與提取。通過仿真和軸承故障實驗，表明提出的方法相比傳統一階隨機共振方法具有更好的提取能力和反噪聲能力，有益于更低信噪比環境的微弱特征增強。然而，提出的方法難以定量描述故障的發展程度，只能定性判斷故障的有無，因此下一步工作將主要研究基于隨機共振的定量故障診斷方法，實現故障發展程度的趨勢預測。

[1]BENZIR， SUTERA A， VULPIANI A.The mechanism of stochastic resonance[J].Journal of Physics A：Mathematical and General，1981，14（11）：453.

[2]譙自健.基于隨機共振理論的微弱信號檢測方法研究及應用[D].蘭州：蘭州理工大學，2015.

[3]潘崢嶸，譙自健，張寧.基于符號序列熵的自適應隨機共振的微弱信號檢測[J].計量學報，2015，36（5）：496-500.

[4]經哲，郭利.隨機共振液壓泵故障特征信號提取[J].中國測試，2016，42（5）：107-111.

[5] 焦尚彬，何童.基于雙穩隨機共振的多頻弱信號檢測[J].計算機工程與應用，2014，50（5）：221-226.

[6]LEI Y G， HAN D， LIN J， et al.Planetary gearbox fault diagnosis using an adaptive stochastic resonance method[J].Mechanical Systems and Signal Processing，2013，38（1）：113-124.

[7]QIAN Z J， LEI Y G， LIN J， et al.An adaptive unsaturated bistable stochastic resonance method and its application in mechanical fault diagnosis[J].Mechanical Systems and Signal Processing，2017（84）：731-746.

[8]LU S L， HE Q B， ZHANG H B， et al.Rotating machine fault diagnosis through enhanced stochasticby full-wave signal construction[J].Mechanical Systems and Signal Processing，2017（85）：82-97.

[9]MATTHEW L B， COLE O T， ANDREW J H， et al.Weak signal detection based on two dimensional stochastic resonance[C]//23rd European Signal Processing Conference，2015.

[10]REBOLLEDO H L F，ESPINOSA G F.Quartic double-well system modulation for under-damped stochastic resonance tuning[J].Digital Signal Processing，2016（52）：55-63.

[11]SHI P M， DING X J， HAN D Y.Study on multi-frequency weak signal detection method based on stochastic resonance tuning by multiscale noise[J].Measurement，2014，47（1）：540-546.

[12]QIAO Z J，PAN Z R.SVD principle analysis and fault diagnosis for bearing based on the correlation coefficient[J].Measurement Science and Technology，2015（26）：14-19.

（編輯：劉楊）

Adaptive second-order bistable stochastic resonance method and its application in weak characteristic enhance detection

LUO Yi
（School of Mechanical Engineering，Guiyang University，Guiyang 550005，China）

An adaptive second-order bistable SR method is proposed to extract bearing fault characteristics in heavy background noise.First，the signal to noise ratio （SNR）of output signal of second-order stochastic resonance system is set as the objection function of colony algorithms.Second，the colony algorithms are employed to select and optimize the system parameters and damping factor.Finally，the optimal parameter pair is used to set the second-order stochastic resonance system to enhance and extract the bearing fault characteristics.Simulation data indicate that the proposed method can effectively extract weak characteristics in heavy background noise.Rolling element bearing case with an incipient roller fault demonstrates that the proposed method possesses strong enhancement capability and is superior to the existing first-order SR methods.The reason is that the proposed method not only selects system parameters adaptively by using colony algorithms，but also is independent on the help of highpass filters.

second-order bistable stochastic resonance； colony algorithms； weak characteristic detection；fault diagnosis

A

1674-5124（2017）06-0031-06

10.11857/j.issn.1674-5124.2017.06.007

2016-11-10；

2016-12-12

羅 毅（1980-），男（彝），貴州貴陽市人，講師，碩士，研究方向為電子信息、信號處理、自動控制。