向量在高考數學解題中的應用

河南省平頂山市理工學校 楊天育 楊龍婷

向量在高考數學解題中的應用

河南省平頂山市理工學校 楊天育 楊龍婷

隨著高考改革的推進，向量知識點得到了越來越多的重視，在近些年的高考中更是成為一大熱點，學生們通過學習向量知識，不僅僅能夠更從容地面對高考，還能利用向量的有關知識進行數學問題的處理，向量思想可以幫助學生們構建更立體的數學思維，進而在做題過程中觸類旁通，很好地處理幾何和代數題目。接下來，筆者從例題入手，簡單介紹如何在高中數學解題過程中更好地運用向量知識。

一、強化記憶向量概念，提升數學解題效率

在近年的高考中，對于向量相關知識的重視程度持續走高，高考《考綱》中明確要求學生們掌握平面向量基本概念及計算，其題型也偏向于概念化、平實化。學生們在進行解題的時候就需要對于向量相關概念有清晰的了解，進而才能在解題的時候胸有成竹。學生們需要熟練掌握向量概念，明白向量在數學領域中所代表的幾何意義，能夠進行基本運算，例如向量加法、減法以及乘法運算，并可以利用坐標系進行平面向量運算的表示。學生們還需要注意做題是對向量相關性質的運用，能夠在拿到題目的時候迅速判斷出向量之間的關系，是屬于相等向量、共線向量還是相反向量，進而進行向量問題的求解。

例如，在2011年四川高考中，就出現了一道利用向量基本概念進行解題的選擇題。如圖所示，在正六邊形ABCDEF中，

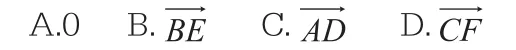
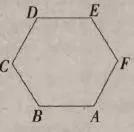
本題中的三個向量看似沒有關系，但是學生們要善于利用向量的基本概念進行解題。因此，學生們在解題的時候，就需要從題目中給出的正六邊形入手，從學生們從前學習過的平面幾何知識可以很容易地知道，正六邊形的六條邊都相等并且對邊兩兩平行,然后學生們再結合題目中的問題，由于要求的是三個向量之和，在圖中很難看出三個向量之間有何種關系，這時候就需要利用輔助線來進行正六邊形的拆分，連接C、E兩點以及B、F兩點，得到向量CE和向量BF，然后利用向量的基本性質找出連接輔助線以后的正六邊形ABCDEF中與所求向量互為相等向量以及相反向量的向量，用代替的值，得出結果為D選項。這道題目的難度并不高，學生們只需要在平時的學習與練習中掌握向量的相關性質，就能夠比較輕松地完成解題。

二、重視基礎向量知識，提升數學解題效率

向量不僅僅是高中數學課程的某一部分章節，由于向量特殊的本質特性，更是作為一項工具來進行應用，利用向量知識可以大大拓寬數學題目的運算形式，從而更好地輔助數學解題。學生們要重視對于向量知識的掌握。在高考中進行有關向量考查的時候，考題往往也脫胎于教材，這樣的出題方式可以從側面反映出學生們在高中階段學習中對于教材知識的掌握程度。學生們只有牢牢把握教材上的相關向量知識點，才能夠在以“立足教材”為核心思想的高考競爭中脫穎而出。學生們在平時可以對于教材上的例題、課后習題等多加練習，在做題的時候深入體會向量基本知識在題目中的運用實例，進而打牢基礎，輕松解題。

例題：在平行四邊形ABCD中做兩條對角線，交點為M，在平行四邊形ABCD所在平面內任意找一點O，試求

這道題屬于基礎題型，并且就是人教A版教材中向量部分的復習題，學生們在平時的學習如果足夠重視教材并且經過了大量的練習，在解題的時候就可以輕車熟路地進行解題。在計算這道題的時候，我們可以先在草紙上畫出相應的平行四邊形，并按照要求連接M點，由于平行四邊形ABCD屬于平面幾何問題，在此題中就要利用到平面向量的有關知識，利用平面向量計算方法進行計算。根據平行四邊形性質可知，對角線交點平分兩條對角線，再將利用向量基本運算以及平行四邊形幾何關系性質進行表示，經過運算即可得出結果

三、鍛煉數形結合能力，提升數學解題效率

數形結合是高中數學中很關鍵的一種數學學習方式，可以將比較復雜的數學問題具象化，繼而學生們就可以比較形象地發現題目中各個變量與條件的關系，進行高效解題，尤其是向量部分知識，本身就具備數形結合的特征，其表示方法就借助了圖象，學生們在學習向量知識的時候就需要具備數形結合的能力，讓學生們在自主做題的時候也能保證對于數學問題的解析能力，可以在解題的時候把幾何問題向量化，完成數與形的轉化，提高了學生的自主學習能力。

例如，在等邊三角形ABC中，在BC上找一點設為D，如果等邊三角形ABC的邊長為3，線段BD長為1，試求的乘積。

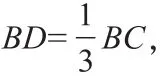
總而言之，向量知識在高考中受到出題人越來越高的重視，在高考題目中往往會將向量的基本概念與性質與其他部分的數學知識進行結合。因此在學習中，學生們應當重視向量部分知識點，回歸教材本身，熟記基礎知識，根據具體題目靈活運用向量性質進行解題，并且在日常學習中構建數形結合的數學思維方式，從而大大提高學生們的做題效率。