導數及其應用問題例析
河北 周 雪
導數及其應用問題例析
河北 周 雪
導數的應用十分廣泛,如求函數的單調區間、極值、最值,求曲線的切線以及解決某些實際問題等.利用導數工具使復雜問題變得簡單化,導數為研究函數的單調性及極值等問題提供了通用的解題思路和方法,因而已逐漸成為新高考的又一熱點.高考對導數的要求主要表現在三個方面,即考查導數的概念、求導的公式和求導的法則;導數的簡單應用,包括求函數的極值,求函數的單調區間,證明函數的增減性等;綜合考查,包括解決應用問題以及有關導數內容的綜合問題.
一、導數的幾何意義
導數的實質是函數值相對于自變量的變化率,體現在幾何上就是切線的斜率.利用導數的幾何意義,研究曲線切線的斜率是導數的重要內容.求切線的方程可通過求導數先得到斜率,再由切點利用點斜式方程得到,求過點p(x0,y0)的切線方程時,一要注意p(x0,y0)是否在曲線上,二要注意該點可能是切點,也可能不是切點,因而所求的切線方程可能不止有1條.
【例1】已知曲線C:y=x3-3x2+2x,直線l:y=kx,且l與C切于點(x0,y0)(x0≠0),求直線l的方程及切點坐標.
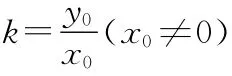
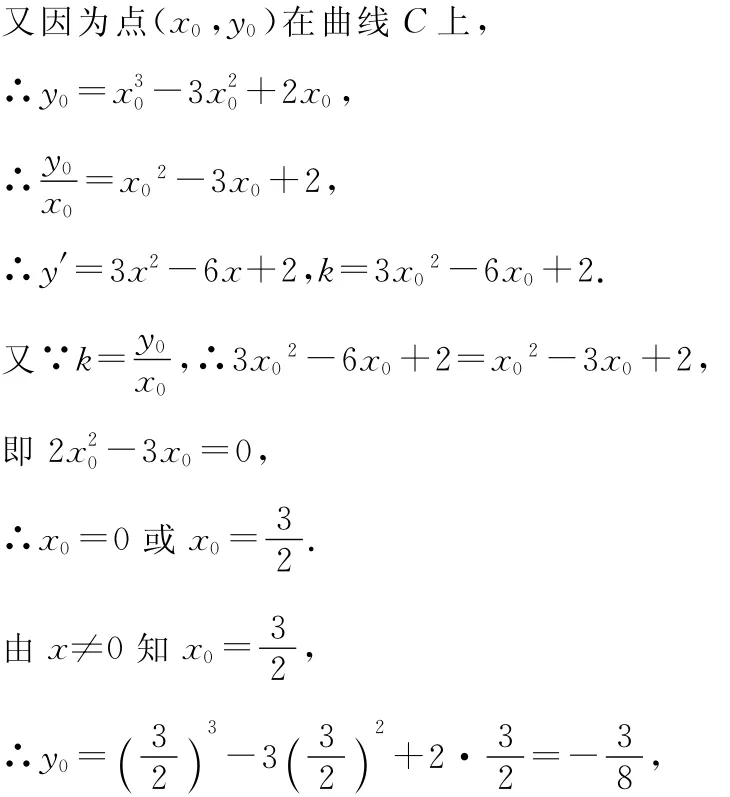
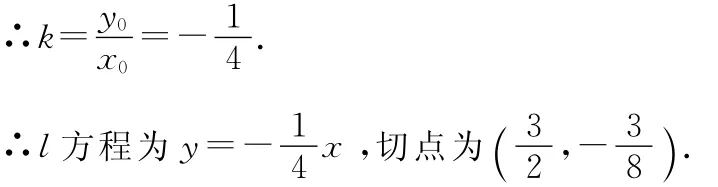
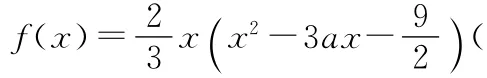


二、運用導數有關知識研究函數的單調性和最值(極值)問題
1.求函數單調區間的步驟:①確定函數的定義域;②求導函數f′(x);③解不等式f′(x)>0,得f(x)的遞增區間;解不等式f′(x)<0,得f(x)的遞減區間.即函數的增區間是f′(x)≥0恒成立的區間,函數的減區間是f′(x)≤0恒成立的區間(其中導數值為零的點為有限個).
利用求導方法討論函數的單調性,要注意以下幾方面:①在某個區間上f′(x)>0(<0)是f(x)在該區間上遞增(遞減)的充分條件而非必要條件;②求單調區間時,首先要確定定義域;然后再根據f′(x)>0(或f′(x)<0),解出在定義域內相應的x的范圍.
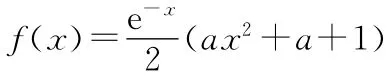
(Ⅰ)判斷f(x)的單調性;
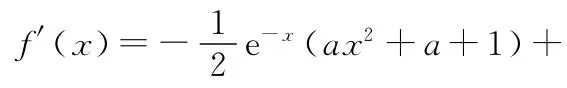
令g(x)=-ax2+2ax-a-1.
①當a=0時,g(x)=-1<0,∴f′(x)<0,
∴f(x)在R上為減函數.
∴g(x)<0,即f′(x)<0
∴f(x)在R上為減函數.
③當a<0時,由-ax2+2ax-a-1>0,
由-ax2+2ax-a-1<0,
(Ⅱ)①當a≥0時,f(x)在[1,2]上為減函數.

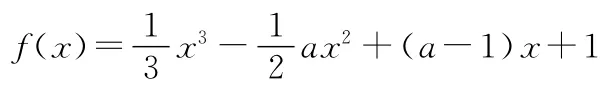
【解析】f′(x)=x2-ax+(a-1).
由f′(x)=0,得x1=1或x2=a-1.
當a-1≤1,即a≤2時,x∈(1,+∞)時,f′(x)>0,
所以f(x)在(1,+∞)內遞增,不合題意.
當a-1>1,即a>2時,x∈(1,a-1)時,f′(x)<0;
x∈(a-1,+∞)時,f′(x)>0,
所以f(x)在(1,a-1)內單調遞減;在(a-1,+∞)內單調遞增.
又由已知得x∈(1,4)時f′(x)<0,x∈(6,+∞)時f′(x)>0,
∴4≤a-1≤6,即5≤a≤7.
2.求可導函數極值的步驟:①求導函數f′(x);②求方程f′(x)=0的根;③檢查f′(x)在方程根左、右的符號,如果左正右負,那么f(x)在這個根處取得極大值;如果左負右正,那么f(x)在這個根處取得極小值.如果左右不改變符號,那么f(x)在這個根處無極值.
【例3】設x=1與x=2是函數f(x)=alnx+bx2+x的值點.
(1)試確定常數a和b的值;
(2)試判斷x=1,x=2是函數f(x)的極大值點還是極小值點,并說明理由.
【解析】

【變式】已知函數fx=ax+bx+cx在點x0處取得極小值-4,使其導數f′(x)>0的x的取值范圍為(1,3),求f(x)的解析式.
【解析】由題意得:

3.利用導數求函數的最值時,首先求f(x)在(a,b)內的極值,然后將f(x)的各極值與f(a)、f(b)比較得出函數f(x)在[a,b]上的最值.具體可分為以下幾步:①求出可導點,即f′(x)=0的解x0;②用極值的方法確定極值;③將(a,b)內的極值與f(a)、f(b)比較,其中最大的為最大值,最小的為最小值;當f(x)在(a,b)內只有一個可導點時,若在這一點處f(x)有極大(小)值,則可以確定f(x)在該點處取到了最大(小)值.
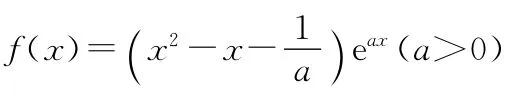
(1)當a=2時,求f(x)的極值;
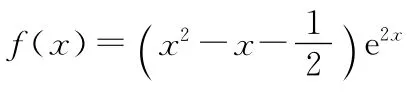
設f′(x)=0得x=±1,那么當x變化時f′(x)及f(x)變化情況如下表:
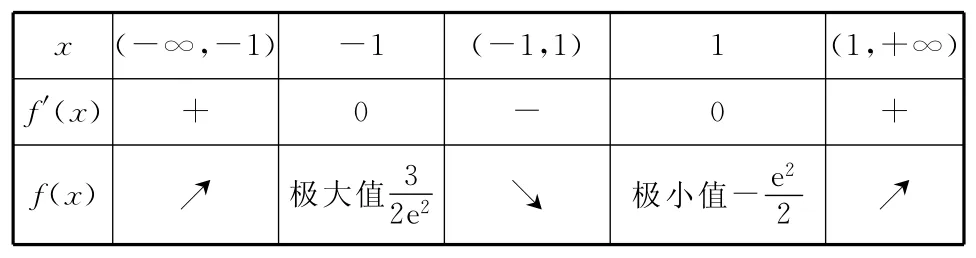
__x (-∞,-1) -1 (-1,1) 1 (1,+∞)f′(x)+____ ____0____ ____-____ ______0+___ f(x) 極大值3________________________2e2 極小值-e22__ ________
令g′(x)=(x-1)(ax+2)eax=0,
所以g(x)最小值為,解得0<a≤ln3.
【變式】已知函數f(x)=x3-ax2+3x.
(1)若f(x)在x∈[1,+∞)上是增函數,求實數a的取值范圍;
(2)若x=3是f(x)的極值點,求f(x)在x∈[1,a]上的最小值和最大值.
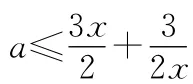
(2)由題意知f′(x)=3x2-2ax+3=0的一個根為x=3,可得a=5,
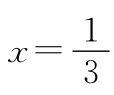
又f(1)=-1,f(3)=-9,f(5)=15,
∴f(x)在x∈[1,5]上的最小值是f(3)=-9,最大值是f(5)=15.
三、利用導數證明等式或不等式
利用導數證明等式或不等式為中學數學引進了新的思路和方法,在證明不等式或等式時,首先要構造函數和確定定義域,其次運用求導的方法來證明.
【例5】已知函數:f(x)=alnx-ax-3(a∈R).
(1)討論函數f(x)的單調性;
(2)若函數y=f(x)的圖象在點(2,f(2))處的切線的傾斜角為45°,對于任意的t∈[1,2],若函數g(x)=x3+在區間(t,3)上有最值,求實數m的取值范圍;
(3)求證:ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)<1+2lnn!(n≥2,n∈N*).
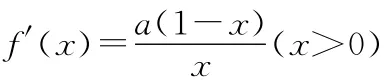
當a<0時,f(x)的單調遞增區間為[1,+∞),單調減區間為(0,1];
當a=0時,f(x)不是單調函數.

由題意知:對于任意的t∈[1,2],g′(t)<0恒成立,
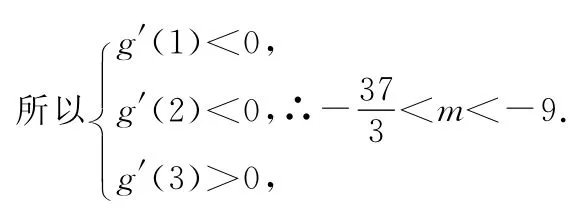
(3)令a=-1(或a=1),此時f(x)=-lnx+x-3,所以f(1)=-2,
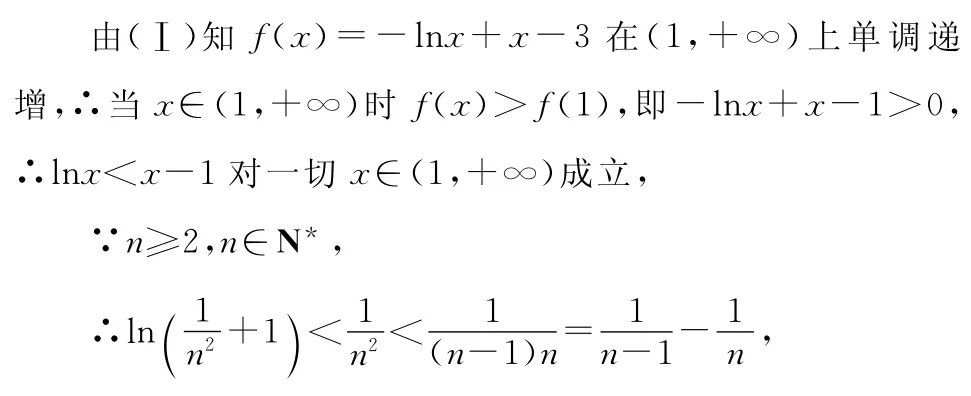
ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)<1+2lnn!(n≥2,n∈N*),
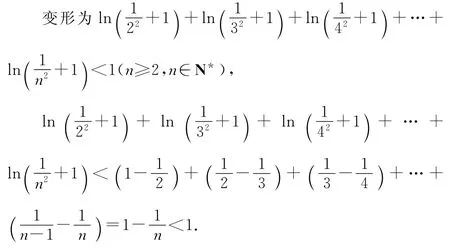
【變式】已知函數f(x)=ex-ln(x+1)-1(x≥0),
(Ⅰ)求函數f(x)的最小值;
(Ⅱ)若0≤y<x,求證:ex-y-1>ln(x+1)-ln(y+1).
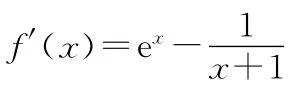
所以當x≥0時,f′(x)≥0,
則函數f(x)在[0,+∞)上單調遞增,
所以函數f(x)的最小值為f(0)=0.
(Ⅱ)由(Ⅰ)知,當x>0時,f(x)>0,
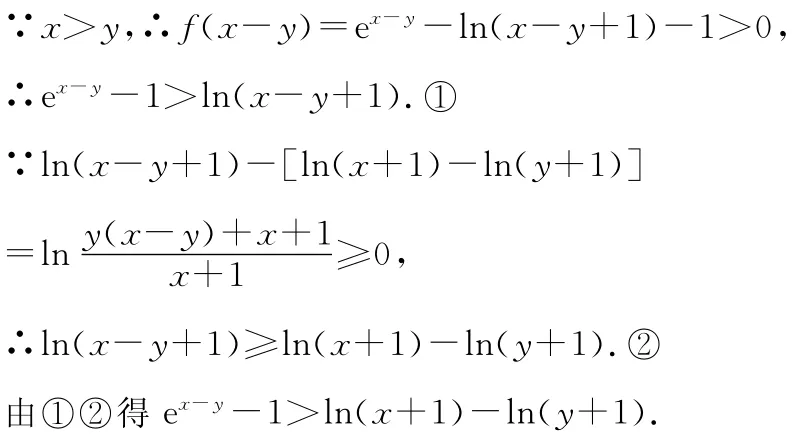
四、導數在實際問題中的運用
導數在自然科學、工程技術等方面都有廣泛的應用,解決實際應用問題關鍵在于建立數學模型和目標函數,把“問題情景”譯為數學語言,找出問題的主要關系,并把問題的主要關系近似化,形式化,抽象成數學問題,再劃歸為常規問題,選擇合適的數學方法求解.難點是如何把實際問題中所涉及的幾個變量轉化成函數關系式.
【例6】煙囪向其周圍地區散落煙塵而造成環境污染.已知A、B兩座煙囪相距3km,其中A煙囪噴出的煙塵量是B煙囪的8倍,經環境檢測表明:落在地面某處的煙塵濃度與該處到煙囪距離的平方成反比,而與煙囪噴出的煙塵量成正比(比例系數為k).若C是連接兩煙囪的線段AB上的點(不包括端點),設AC=xkm,C點的煙塵濃度記為y.
(Ⅰ)寫出y關于x的函數表達式;
(Ⅱ)是否存在這樣的點C,使該點的煙塵濃度最低?若存在,求出AC的距離;若不存在,說明理由.
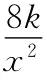
解得x=2.
故當0<x<2時,y′=0.當2<x<3時y′>0.
可見當x=2時,y取得極小值,且是最小值.
即在連接兩個煙囪的線段AB上,距煙囪A處2km處的煙塵濃度最低.
【變式】在甲、乙兩個工廠,甲廠位于一直線河岸的岸邊A處,乙廠與甲廠在河的同側,乙廠位于離河岸40km的B處,乙廠到河岸的垂足D與A相距50km,兩廠要在此岸邊合建一個供水站C,從供水站到甲廠和乙廠的水管費用分別為每千米3a元和5a元,問供水站C建在岸邊何處才能使水管費用最省?

導數是函數、解幾的交匯點,有著重要的工具作用,豐富了對函數研究的方法,現在已是新高考重點考察的基礎知識,成為高考數學的一大熱點,相信高考仍然是會重點考查的,所以考生要引起高度的重視.
(作者單位:河北省衡水市第二中學)

