微通道分流彈狀流的界面過程及壓力演變規律

陳宏霞，黃林濱，宮逸飛

?

微通道分流彈狀流的界面過程及壓力演變規律

陳宏霞1,2，黃林濱1，宮逸飛1

（1華北電力大學能源動力與機械工程學院，北京102206；2低品位能源多相流與傳熱北京市重點實驗室，北京102206）

彈狀流分流不僅能調控兩相流流型從而強化傳熱，同時也是生物化工、制藥行業的傳統過程。針對壁面微通道分流液相、調控兩相流型的過程進行數值模擬，獲得局部參數變化規律，是獲得兩相流流型演變機理的基礎。采用VOF模型耦合動態自適應網格精準追蹤氣液界面，模擬氣液界面在分液口的界面運動；獲得軸向及壁面靜壓、動壓的演變規律。通過模擬可知微通道分流彈狀流的關鍵是氣彈在分液口的類活塞運動；同時由于界面拉普拉斯壓力差的存在，彈狀流壓降具有不連續性；且此不連續壓力隨氣彈在分液口的類活塞運動具有周期波動性。而彈狀流液橋部分的局部壓降是影響總壓降的關鍵；近氣彈頭部的液相區壓降顯著，近氣彈尾部的液相區域由于液速降低其壓降明顯衰弱；此為彈狀流有別于其他兩相流流型的壓降特點。

彈狀流；分液；局部壓力；CFD；模擬

引 言

彈狀流是氣液兩相流的重要流型，其流型特征參數（氣彈長度、液橋長度、液膜厚度及含氣率）直接影響彈狀流的流動傳熱性能。對彈狀流進行氣液分離可改變彈狀流氣彈/液橋長度比、提高含氣率、降低液膜厚度，從而調控流型強化傳熱[1]。經歷重力分離[2-3]、離心力分離[4-5]、微通道分離[6-7]，本課題組提出在表面張力和毛細力作用下利用毛細結構進行流型調控、分離兩相流、強化傳熱的新思想[8-9]，受到國內外的廣泛關注[10-11]。

經過系列的實驗研究，驗證了內分液以及外分液微結構對兩相流流型調控的成效及基本原理，并獲得了初步的調控數據[8-10]。而對于微通道內兩相流的界面捕捉以及相分離的機理研究，僅通過實驗研究很難準確、詳實地獲得其流動場、壓力場及分離原理，其必然依賴并結合快速發展的計算機技術及數值模擬方法。

Sotowa[12]、Fang等[13]、Gupta等[14]、Zenith等[15]采用VOF模型對微/小通道內的兩相流進行模擬，深入研究表面張力以及摩擦力對氣液分離的作用。Wiesegger等[16]結合實驗和CFD模擬對不同形狀T型、V型、G-V-L型多種相分離過程進行研究，指出綜合利用重力、毛細力及離心力才能獲得較好的分離效果；且隨慣性力增大，毛細力對分離效果影響很小。無論實驗研究還是數值模擬研究，主要目標參數均為兩相流分離效果，對于其機理的分析僅限于入口形狀、角度以及氣液流速對其分離效果的影響。而對于彈狀流的氣液兩相分離，其主要原理為氣泡從大通道進入小通道需要消耗一定的表面能，此表面能與界面壓力和界面曲率有關，即界面壓力或壓力差為彈狀流氣液分離的源動力。

彈狀流的壓力研究主要集中在沿程壓降的測定，并建立相應模型[17]。經典的均勻模型(HFM)、非均勻模型(SFM)對于兩相流壓降的求解，對不同流型具有一定的適應性。例如由于液體流場受小氣泡壓力擾動較小，HFM可以很好地預測泡狀流壓降[18-19]；而對于彈狀流等間歇流存在一定的偏差。同時SFM基于氣液分開流動的假設，忽略氣液相互作用、界面壓差的存在，仍不能準確表述彈狀流壓降特點。Taha等[20-21]利用Fluent數值模擬方法模擬彈狀流壓降，指出流動單元內部壓降與毛細數具有非線性關系，氣彈前緣的界面壓降隨毛細數的增大而增大。Zhao等[22]運用Boltzmann方法研究氣液兩相流流動及壓降，指出兩相流壓降的不連續性發生在相界面，界面處拉普拉斯壓力在氣液界面引起壓力跳躍；同時主要針對氣相部分的壓降，指出氣相壓降相對液相壓降微乎其微；對于液相局部壓降并未涉及。Chen等[23]、Langwisch等[24]研究彈狀流局部壓降規律，暗示液橋內壓降為非線性，且近氣彈尾部壓力變化更復雜。

目前對于彈狀流局部壓降、界面運動的研究尚少，而對于間歇流分離、生物藥物運輸、石油破乳等應用，界面運動及界面壓力的認知是人工控制的基礎和前提。本文利用CFD數值模擬方法，針對T型壁面微孔分離氣液兩相流、調控彈狀流流型的過程進行研究；深入研究彈狀流通過分液結構過程中界面運動及軸向局部壓力、壁面壓力以及分液界面壓力的演變規律，獲得分液機理，為兩相流的人工可控奠定基礎。

1 計算模型

1.1 物理模型及計算方法

T型分液結構調控彈狀流的物理模型如圖1所示。兩相流主管道全長101 mm，直徑2 mm；為了分析多個分液孔相互作用，在距離進口51 mm處設置3個間距為0.2 mm、孔徑為0.2 mm的壁面T型分液結構，長度為5 mm；3個分液出口1、2、3記為drainage1、drainage2、drainage3。利用Ansys流體力學軟件模擬時，利用軸對稱方法只模擬通道的1/2，忽略重力影響。

數值計算采用二維雙精度求解器；選用VOF方法，壓力隱式求解，耦合修正的HRIC算法進行界面捕捉。HRIC是一種順風與背風非線性混合的差分模型，其在界面捕捉上具有較好的精準度。利用CSF連續表面張力模型計算界面表面張力，壁面為無滑移流動。計算過程采用壓力與速度耦合求解，求解方式為PISO；壓力離散選擇PRESTO，動量選擇二階迎風格式離散。其他常數采用默認值。

1.2 假設及邊界條件

假設條件如下。

（1）為更好地研究表面張力作用，取消重力影響，本文計算過程不考慮重力，=0。

（2）流動過程，流體物性密度、黏度、表面張力均為常數。

（3）分液結構前管道長度為管道半徑（）的50倍，認為彈狀流流型在分液前達到充分發展狀態。

邊界條件如下。

（1）入口速度分區設置：中間氣液混合入口、管道邊緣穩定液相入口稱為液膜入口，具體尺寸和參數見表1。

（2）入口壓力給定初始條件為500 Pa。

（3）出口邊界條件采用壓力出口，outlet= 0；氣相回流比為0。

（4）3個分液口邊界條件設置為壓力出口，outlet= 500 Pa；氣相回流比為1。

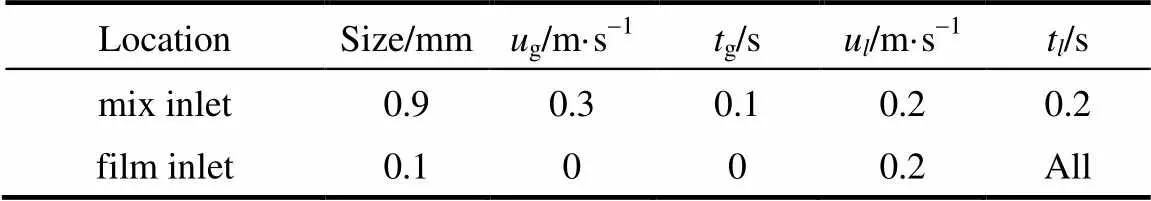
表1 入口分區參數設置

Note: All sizes in Table 1 are semi-size of model for its axial symmetry.

1.3 網格劃分

模擬物理模型的長度為101 mm，管道直徑為2 mm，微細分液結構直徑為0.2 mm；整個物理模型存在3種不同尺度的空間結構，對于此復雜尺度結構，采用單一網格系統，網格數量將異常龐大，對于非穩態兩相流動問題，計算很難實現。為此本文針對不同空間結構采用不同尺度的網格系統：光管區域和核心區域網格長度平均為0.1 mm、寬度為0.075 mm；利用公式計算主管道邊界層厚度為0.25 mm，設置邊界層網格10層，網格尺寸過渡倍數為1.3倍，最底層網格為0.006 mm；分液孔結構內同樣利用邊界層網格設置底層網格為0.006 mm，中間網格寬度為0.015 mm，網格數量約為30萬個。同時，為了精確捕捉運動氣泡兩相界面、液膜厚度及氣液界面在分液孔交接處的運動規律，本文采用網格動態自適應技術對相界面處的網格進行二級加密。相界面處的網格被細化16倍，僅為單一網格系統網格數量的0.6%，網格數量大幅減小。

為驗證網格無關性，Gambit軟件分別劃分網格26萬、30萬、36萬個，并附加二階界面動態自適應網格；結果證明，當網格數達到30萬個，在相同邊界條件下氣彈和液橋長度變化微小，液膜輪廓均清晰可見。同時針對彈狀流的薄液膜厚度這一參數，進行了模擬結果與經典計算公式之間的比較，如表2所示。

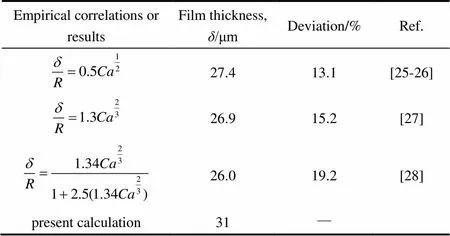
表2 計算液膜厚度和經典計算公式的對比結果

表3為模擬分液效果與前述小尺度實驗結果的比較。由表可知，流型調控前后氣液長度比與實驗結果的偏差均在12%以內，證明此網格劃分密度已達到網格無關性要求，且可獲得精準的彈狀流流型模擬結果。因此，為了盡量減小計算工作量，本文選用30萬個網格進行模擬計算，對T型微通道內界面運動及流場進行研究。

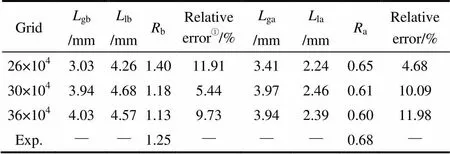
表3 模擬氣彈、液橋長度及長度比與實驗結果的比較

Note:Relative error is calculated length ratio to experimental length ratio of bubble and liquid bridge.

2 模擬結果

2.1 彈狀流流型及壓降

如圖2所示為彈狀流流型、壓降規律，入口速度分別為0.3、0.2 m·s-1，流動穩定后為標準的彈狀流流型，氣彈、液橋長度分別為3.94、4.68 mm。由圖可知，伴隨彈狀流氣彈和液橋的間隔分布，軸線靜壓呈現梯級階躍；階躍的高度差即存在于氣彈界面處的拉普拉斯壓差，DP=91 Pa。軸向沿程壓降和壁面沿程壓降分別為DA= 4.58 kPa·m-1、Dw= 5.21 kPa·m-1。由軸向壓力隨流型變化規律可知，相對于氣彈內部壓力的穩定，液橋內部流動更加復雜。在近氣泡前端的液橋區內液速相對較大，軸向壓力迅速下降；而在近下游氣泡區域內由于下游氣泡對中央氣泡的阻擋，軸向壓力呈現反彈式波動。軸向沿程壓降主要取決于液橋內部壓降的大小。彈狀流對管道壁面的壓力則主要取決于局部流型對壁面的剪切力。液橋主體沿壁面的流動邊界層相對穩定；僅在下游氣泡的尾部區域，液體進入薄液膜區域前存在渦流，流動邊界層厚度及壁面壓降呈現波動，如圖2所示。一旦進入薄液膜區域，在整個微米級厚度的流動區域內流動邊界層幾乎消失，流場對壁面的剪切力及壓力迅速增大；并在薄液膜區域內的渦流處達到最大值，之后逐漸降低。

2.2 彈狀流分流前后流型變化

流經壁面微通道時，分液管內僅分離液體，無氣泡排出。分液后彈狀流氣彈的長度（ga=3.97 mm）幾乎保持不變，液橋長度由分液前的4.68 mm縮短為2.46 mm；氣液長度比由0.84增大到1.61，如圖3(a) 所示。同時，由氣彈輪廓及液膜厚度變化[圖3(b)]可知，分液前氣泡為標準的子彈形狀，前端曲率大，末端底座曲率小；當氣泡抵達分液口，在表面張力的作用下氣泡受阻攔，氣泡前端曲率降低；伴隨液體從分液通道排出，液相對分液后的氣泡界面存在與流動方向相反的剪切力，氣泡前后曲率趨于一致，氣泡輪廓由分液前的子彈形轉變為對稱形狀。將氣泡到壁面之間的液膜分為氣泡前端厚液膜區、末端厚液膜區以及中間薄液膜區。可知，分液前后氣彈薄液膜長度film及薄液膜厚度film變化甚微，分別為1.5 mm和33mm。由于氣泡輪廓變化，在厚液膜區內按平均分配氣泡長度的原則分別測量分液前后最大、最小及中間液膜厚度maxmidmin；計算算數平均值獲得厚液膜區的平均液膜厚度ave。可知，由于氣相體積不變，氣泡長度變化甚微可忽略，即氣泡輪廓面積一致，相對應厚液膜的平均厚度亦相等，為0.41 mm。因此，本文微通道分液后，彈狀流氣泡雖形狀有略微不同，但體積不變、薄液膜厚度及厚液膜平均厚度未改變；僅液橋長度縮短為原來的52%。對氣泡界面曲線進行積分求得氣液相體積，并獲得分液前后的體積氣含率。

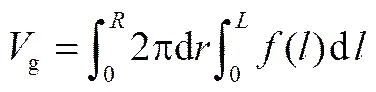
V=1-g+2pRL(2)

(3)

式中，、分別為半徑方向及流動方向上的長度；、分別代表主管道半徑和最大長度；下角標g、分別代表氣液兩相；代表體積；為體積氣含率。本文工況下分液后氣含率由原來的0.33提高到0.44。

2.3 分液前后流場及壓力場分布規律

分液過程穩定后，分液通道前后的流動單元數目保持不變；即入口進入一個流動單元的周期與出口一個流出單元時間相等；流動單元的長度與氣液兩相平均速度呈正比，如式（4）所示。

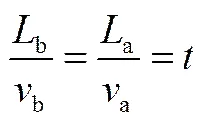
由2.2節流型變化規律可知，氣泡和液橋組成的流動單元長度分液后縮短為原來的67%，即分流后平均流速降低為原來的67%。圖4(a)為分液前后流動單元的速度場分布。氣彈薄液膜區域內，回流液相與上游正向流動液體相遇在尾部形成兩個渦流區。在液橋中心區，液體受氣彈向前的推力，同時受下游氣彈的阻擋，形成周圍低速中間高速的平臺流場。分液后，由于部分液體流量的分離，液橋長度變短，彈狀流整體平均流速降低為原來的67%；液橋內部平臺流場速度梯度顯著削弱；同時低速液相相對氣泡的剪切力增大，在薄液膜區域處的回流更顯著。

由圖4(b)局部壓力分布及壓力變化曲線可知，除氣液界面表面張力引起的拉普拉斯壓力跳躍以外，液橋內部壓力變化規律比氣彈內部的壓力分布更為復雜，整個液橋段動壓能分布不均勻。沿軸線方向，液橋段存在高動壓能到低動壓能轉變的波動變化；由局部動壓曲線可知液橋內高動壓區與低動壓區的轉折點如圖4所示。而沿徑向方向，近氣彈頭部液橋區域的管道中心動壓高，近壁面區域動壓低。近下游氣彈尾部的液橋區域則出現中心低壓區、壁面高壓區的分布規律；尾部壁面高壓區的存在使得液橋內部靜壓曲線在尾部呈現如圖4所示波動。彈狀流經微通道分液后，液橋內動壓能沿軸向的波動轉折點提前；高動壓區長度由占原來液橋總長度的62%降低為57%；高壓區范圍減小，低壓區范圍相對增大，相對氣彈對液相的推進力，液相對氣相的阻滯作用更加顯著。同時，分液后液橋動壓的不均勻度相對削弱，高動壓區和低動壓區的壓差減小。

如圖5所示，沿程壓降中靜壓壓降占優，動壓由于速度保持穩定基本維持平均值不變的周期性波動。當彈狀流液橋位于分液微通道與主管道交匯處時，主管道上游和下游流體聯通，伴隨部分液體的分離管內流速降低，分液后管內沿程靜壓壓降顯著減小；由分液前的4.4 kPa·m-1降低為2.12 kPa·m-1。而當氣彈到達分液口，氣彈沿微通道滲透生成3個子氣泡。子氣泡在分液微通道內做“類活塞”運動的同時，主管道內上下游流體被切斷。此時，分液微通道出口的恒定背壓（500 Pa）通過子氣泡的界面壓差傳遞至主管道。主管道內靜壓力由分液微通道處的氣彈向進、出口兩側擴展。使得分液口下游到出口處的沿程總壓降為固定值500 Pa，即最大的沿程壓降8.96 kPa·m-1。彈狀流的氣彈、液橋交替流經分液口，使得管內壓力分布也隨之表現為周期性波動，此為彈狀流局部壓力周期不穩定性在分液操作中的特征表現。

2.4 各分液口的分液量

圖6為進口和各個出口的流速情況。已知氣、液兩相在進口流入時間周期為1:2，所有出口流速都按彈狀流氣液兩相標識出一個流動單元的時間周期。出口處氣液的標識代表出口截面的主相，排液口處的氣液標識表示交替流經分液交匯處的彈狀流氣液兩相。可知，出口處由于氣彈排出時界面發生變形，出口截面處液體流速在氣彈長度范圍中逐漸增大；氣彈尾部到達出口時，涌來的液橋由于界面壓差的瞬間消失引起流速的突然增大，隨后又回歸穩定；且由于界面壓差的突然消失，流速最大值出現在氣彈排出后的瞬間。同時，3個排液微通道具有與出口流速類似的非均勻性和周期波動性。由于液橋高速區內近壁面處液體向上游薄液膜區域的回流，徑向分速度使第1分液通道在液橋的高速區達到分液口時即開始分液。同時，由于第1通道液體的排出阻截下游近壁面區液相向薄液膜的回流，導致第2和第3個分液口在液橋區無液體分離。當氣彈到達通道交匯處時，氣彈生成滲透子氣泡并在分液通道內做“類活塞”運動[29-30]，此時在子氣泡的推動下發生分液。如圖所示第2與第3個分液通道的分液間隔為0.003 s；通道之間間隔為0.2 mm，氣彈流動速度為0.067 m·s-1。可知，氣彈到達分液通道后，在界面壓差的作用下形成子氣泡并進行類活塞運動，阻滯了氣彈在主管道內的流動，使其流速顯著降低。同時利用對出口流速曲線的面積分獲得3個分液口的分液量為52:26:22。

2.5 分液交叉管處界面運動及壓力演變

中心軸線的壓力變化可反映流型的演變，沿壁面及分液口處的靜壓及動壓變化則能揭露分液過程的機理。如圖7(a)所示，整個彈狀流氣泡從接近分液口到完全脫離需要約16 ms；而每個微通道內滲透子氣泡歷經約10 ms，經過生長、穩定滑移、回縮以及脫離的整個界面運動周期，進行液體分離。如圖7(b)所示，當液橋高動壓區達到分液口時，微通道內靜壓能經過低動壓區的補償已經為正值；在微通道入口處開始出現動能。而結合圖6出口排液流速可知，此時第2、第3個微通道流入的液體主要用于補充子氣泡回縮造成的空白體積，并未造成分液；第1個微通道滲透子氣泡的體積相對很小，流入液體量大于所需補充體積即引發分液。到達圖7(c) 時刻，第1、2分液口被氣泡封堵，入口流速為0，其靜壓力受分液出口影響迅速上升；而第3分液口仍處在補液狀態，靜壓相對較低。當3個微通道均被滲透子氣泡填充，入口速度及動壓消失；靜止氣泡發揮背壓閥的作用，管內靜壓與分液出口壓力相同達到最大值；僅在液膜的慣性作用下，在第1個分液口有極少液體的滲流。結合圖6，可知此時為子氣泡的生長過程，雖分液入口處速度和動壓為零，而在子氣泡延伸生長的作用下微通道出口進行排液。當子氣泡生長到最大長度后開始回縮，管內流動出現倒流，靜壓逐漸降低。第1子氣泡脫離通道后液體涌入并進行液體補充，如圖7(e)所示。伴隨全部子氣泡活塞式的抽離，分液入口處靜壓瞬間變為負值，此時為液橋低動壓區抵達分液入口。主管道液體流入微通道補充靜壓損失而不產生分液。經液橋低動壓區的液體補充，分液口靜壓逐漸恢復為正值，并進入下一個循環周期。可知彈狀流分液實質是：彈狀流氣彈封堵分液微通道，在無流體流入分液口的情況下，伴隨滲透子氣泡的生長，子氣泡將微通道內液體排出體系；而當液橋抵達分液口時，子氣泡的回縮及抽離階段使分液微通道內產生負壓，并吸入液橋中液體進行補充，但不引起分液。整個分液過程伴隨氣彈和液橋的交替出現及氣彈的類活塞封堵，管內靜壓呈現正負周期振蕩規律。

3 結 論

通過對微通道調控彈狀流分液過程的模擬，指出其流型調控分液過程的實質；并對分液過程中軸向沿程壓力、局部壓力以及壁面及分液口的壓力變化規律進行分析和討論，獲得如下結論。

（1）彈狀流經過壁面微通道時，分液管內僅分離液體，無氣泡排出。在本工況下，分液后彈狀流氣彈的長度幾乎保持不變，僅液橋長度縮短為原來的52%；分液后管內氣含率由原來的0.33提高到了0.44。3個分液口的分液量之比為52:26:22，首個分液量占主導。

（2）相對于氣彈內部壓力的穩定，彈狀流液橋內部流動更加復雜。在近氣泡前端的液橋區內為高動壓區；而在近下游氣泡區域內為低動壓區。對應液橋內部靜壓的變化在高動壓區勻速下降，而在低動壓區呈現反彈式波動。分液后，液橋內動壓能沿軸向的波動轉折點提前；高壓區范圍減小，低壓區范圍相對增大，相對氣彈對液相的推進力，液相對氣相的阻滯作用更加顯著。同時，分液后伴隨液速的降低，液橋動壓、靜壓的不均勻度相對削弱，高動壓區和低動壓區的壓差減小。

（3）伴隨彈狀流的氣彈、液橋交替流經分液口及氣彈的類活塞封堵，管道內部壓力表現為周期性波動，主要體現在管內靜壓呈現正負周期振蕩規律。此為彈狀流局部壓力周期不穩定性在分液操作中的特征表現。

（4）微通道分液彈狀流實質是：彈狀流氣彈封堵分液微通道，在無流體流入分液口的情況下，伴隨滲透子氣泡的生長，子氣泡將微通道內液體排出體系；而當液橋抵達分液口時，子氣泡的回縮及抽離階段使分液微通道內產生負壓，并吸入液橋中液體進行補充，但不引起分液。

References

[1] CHEN H X, XU J L, WANG W. Internal liquid separating hood-type condensation heat exchange tube: US13/984659[P]. 2015-04.

[2] 彭曉峰, 吳迪, 張揚. 高性能冷凝器技術原理與實踐[J]. 化工進展, 2007, 26(1): 97-104. PENG X F, WU D, ZHANG Y. High performance technology of the condenser[J]. Chemical Industry and Engineering Progress, 2007, 26(1): 97-104.

[3] HE K, WANG S, HUANG J. The effect of flow pattern on split of two-phase flow through a micro-T-junction[J]. International Journal of Heat Mass Transfer, 2011, 54: 3587-3593.

高速公路工程中的中心試驗室，能夠為工程中的技術人員提供精確的試驗數據，并幫助工程管理人員制定科學有效的施工質量管理制度。但是，由于高速公路工程中的中心試驗室缺乏一定的權威性，受外界影響較大，嚴重影響高速公路工程中各項試驗結果的準確性，降低工程的施工質量管理水平。想要更好地提升高速公路工程中心試驗室的權威性，中心試驗室的工作人員要與業主方、總監辦方進行合理溝通，有效保證中心試驗室各項工作的順利進行。

[4] WILLEME G P, VAN ESCH B P M, BROUWERS J J H,Creeping film model for condensed centrifugal separation processes[J]. Chemical Engineering Science, 2008, 63: 3358-3365.

[5] MA Q, HU D, HE G,Performance of inner- core supersonic gas separation device with droplet enlargement method, separation science and engineering[J]. Chinese Journal of Chemical Engineering, 2009, 17 (6): 925-933.

[6] HIBARA A, IWAYAMA S, MATSUOKA S,Surface modification method of microchannels for gas-liquid two phase flows in microchips[J]. Analysis Chemistry, 2005, 77: 943-947.

[7] HSIEH C C, YAO S C. Development of a microscale passive gas-liquid separation system[C]//Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 2004: No.566.

[8] CHEN H X, XU J L, LI Z J,Stratified two-phase flow pattern modulation in a horizontal tube by the mesh pore cylinder surface[J]. Applied Energy, 2013, 112: 1283-1290.

[9] 陳宏霞, 徐進良, 李子衿, 等, 新型外分液結構調控水平管間歇流流型[J].化工學報, 2012, 63(11): 3470-3477. CHEN H X, XU J L, LI Z J,Intermitted flow pattern modulation by outward phase separation[J]. CIESC Journal, 2012, 63(11): 3470-3477.

[10] CHEN H X, XU J L, XIE J,. Modulated flow patterns for vertical upflow by the phase separation concept[J]. Experimental Thermal and Fluid Science, 2014, 52: 297-307.

[11] CHEN Q C, XU J L, SUN D L,. Numerical simulation of the modulated flow pattern for vertical upflows by the phase separation concept[J].International Journal of Multiphase Flow, 2013, 56: 105-118.

[12] SOTOWA K I. Performance evaluation and integration of micro devices for singe stage distillation[D]. Japan: Kyushu University Fukuoka, 2003.

[14] GUPTA R, FLETCHER D F, HAYNES B S. On the CFD modelling of Taylor flow in microchannels[J]. Chemical Engineering Science, 2009, 64: 2941-2950.

[15] ZENITH F, KRAUS M, KREWER U. Model-based analysis of micro-separators for portable direct methanol fuel-cell systems[J]. Computer ＆Chemical Engineering, 2012, 38: 64-73.

[16] WIESEGGER L E, KNAUSS R P, GUNTSCHNIG G. E,Vapor-liquid phase separation in micro-/ministructured devices[J]. Chemical Engineering Science, 2013, 93: 32-46.

[17] ASADI M, XIE G N, SUNDEN B. A review of heat transfer and pressure drop characteristics of single and two-phase microchannels[J].International Journal of Heat and Mass Transfer, 2014, 79: 34-53.

[18] CHOI C, KIM M. Flow pattern based correlations of two-phase pressure drop in rectangular microchannels[J]. International Journal of Heat Fluid Flow, 2011, 32: 1199-1207.

[19] VENKATESAN M, DAS S K, BALAKRISHNAN A R. Effect of diameter on two-phase pressure drop in narrow tubes[J]. Experimental Thermal and Fluid Science, 2011, 35: 531-541.

[20] TAHA T, CUI Z F. Hydrodynamics of slug flow inside capillaries[J].Chemical Engineering Science, 2004, 59(6): 1181-1190.

[21] TAHA T, CUI Z F. CFD modelling of slug flow inside square capillaries[J]. Chemical Engineering Science, 2006, 61(2): 665-675.

[22] ZHAO Y, ORIN H, FAN L S. Experiment and lattice Boltzmann simulation of two-phase gas-liquid flows in microchannels[J]. Chemical Engineering Science, 2007, 62(24): 7172-7183.

[23] CHEN Y, KULENOVIC R, MERTZ R. Numerical study on the formation of Taylor bubbles in capillary tubes[J].International Journal of Thermal Sciences, 2009, 48(2): 234-242.

[24] LANGWISCH D R, BUONGIOMO J. Prediction of film thickness, bubble velocity, and pressure drop for capillary slug flow using a CFD-generated database[J]. International Journal of Heat and Fluid Flow, 2015, 54: 250-257.

[25] TAYLOR G L. Deposition of a viscous fluid on the wall of a tube[J]. Journal of Fluid Mechanics, 1961, 10: 161-165

[26] FAIRBROTHE F, STUBBS A E. The bubble-tube method of measurement[J]. Journal of the Chemical Society, 1935, 1: 527-529.

[27] BRETHERTON F P. The motion of long bubbles in tubes[J]. Journal of Fluid Mechanics, 1961, 10: 166-188.

[28] AUSSILLOUS P, QUERE D. Quick deposition of a fluid on the wall of a tube[J]. Physics of Fluids, 2000, 12(10): 2367-2371.

[29] CHEN H X, XU J L, YAN Y Y,Phase separation and air-water flow pattern modulation by a micro-channel drainage system[J]. Applied Thermal Engineering, 2017, 122: 214-226.

[30] 陳宏霞, 黃林濱, 宮逸飛. 壁面分流調控彈狀流流型的CFD數值研究[C]//工程熱物理會議. 廣州, 2016: 11-14. CHEN H X, HUANG L B, GONG Y F. CFD study on the flow pattern modulation of slug flow by liquid separating structure on the wall[C]//Engineering Thermal Physical Conference. Guangzhou, 2016: 11-14.

Pressure evolution and interface movement of slug flow during micro-channel modulation process

CHEN Hongxia1,2, HUANG Linbin1, GONG Yifei1

(1School ofEnergy Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China;2Beijing Key Laboratory of Multiphase Flow and Heat Transfer, Beijing 102206, China)

Slug flow separation, a traditional process in biochemical and pharmaceutical industries, is a valid method to control two-phase flow patterns and enhance heat transfer. The fundamental to study evolution mechanism of two-phase flow patterns is to understand development rules of local parameters by numeric simulation of drainage on micro-channel walls and modulation process of slug flow. The VOF model coupling with dynamic grid adaption was chosen to precisely track gas liquid interface, to simulate movement of the interface at split, and to acquire hydrostatic and dynamic pressure evolution along axial direction and at wall. Results indicated that piston-like movement of bubbles at split was critical to slug flow separation in micro channels. Because of the presence of Laplacian pressure drop at the interface, pressure drop of slug flow was discontinuous with a periodic wavy variation following the interface piston-like movement. The overall pressure drop of slug flow was influenced by local pressure drop at liquid bridge region. Significant pressure drop near bubble head while minimal pressure drop near bubble tail where liquid flow rate was reduced. Such pressure drop characteristics of slug flow is distinguished from other two phase flows.

slug flow; liquid separation; local pressure; CFD; simulation

10.11949/j.issn.0438-1157.20170064

TK 121

A

0438—1157（2017）08—3030—09

陳宏霞（1980—），女，博士，副教授。

國家自然科學基金項目（51576063）；中央高校優青項目。

2017-01-16收到初稿，2017-05-05收到修改稿。

2017-01-16.

CHEN Hongxia, hxchen@ncepu.edu.cn

supported by the National Natural Science Foundation of China(51576063) and the Universities’ Basic Scientific Research of Central Authorities.