基于熱載荷和索張力的平面薄膜邊界形狀優化

賀 群，保 宏?，杜敬利，彭福軍

基于熱載荷和索張力的平面薄膜邊界形狀優化

賀 群1，保 宏1?，杜敬利1，彭福軍2

（1?西安電子科技大學電子裝備結構設計教育部重點實驗室，西安710071；2．上海宇航系統工程研究所，上海201108）

針對平面薄膜相控陣天線受器件熱以及邊界索張力不確定的影響，提出一種平面薄膜相控陣天線邊界形狀優化方法。首先，考慮到天線單元的熱效應，建立了平面薄膜天線熱?結構有限元分析模型。其次，在確定范圍內的任意索張力組合下，將薄膜邊界形狀視為3次B樣條曲線，以曲線控制點位移為設計變量建立平面薄膜天線優化模型，通過優化實際結構索膜應力與參考應力偏差，實現對薄膜邊界形狀的優化。最后，通過數值模擬驗證了該方法的有效性。與目前薄膜天線邊界形狀相比，該方法可實現任意曲線形狀優化。

平面薄膜天線；器件熱；索張力組合；邊界形狀優化

1 引言

由于平面薄膜相控陣天線具有質量輕、收納比大、波束掃描靈活等特點，其概念一經提出即成為研究的熱點［1?2］，而薄膜邊界形狀直接影響結構的固有頻率、應力分布等，成為其結構設計主要內容。合適的邊界形狀對減少褶皺，提高膜面精度意義重大。目前對平面薄膜天線邊界形狀的研究主要集中在拋物線、圓弧形和橢圓形狀。

2001年，Fang［3］研究了平面薄膜天線的邊界形狀和張拉系統，給出了拋物線薄膜天線的設計方程，得出管道張拉系統能夠使懸索張力分布更加均勻、減少褶皺產生的結論。2003年，Gyula［4］在理論上證明了當薄膜邊界承受單軸等值拉力時形成的邊界形狀為拋物線，得到了拋物線懸索切應變拉壓變換的轉折點，為避免褶皺產生，提出將承受壓縮應變的懸索曲線翻轉為拱形，從而獲得受壓的能力。由于翻轉后的曲線與原曲線的過渡位置應力集中較嚴重，且這兩種曲線的平滑過渡問題難以解決，該方法沒有應用在工程實際。2005年，Johanne C Heald［5］針對一種多層拋物線平面薄膜天線，優化了其曲線跨度和垂度。

2004年，Sakamoto［6］從理論上證明，圓弧狀邊界薄膜上各點處于雙軸等值拉伸應力狀態，膜內應力為最佳張緊狀態，并建立圓弧花瓣狀薄膜模型，并以天線有效面積和總質量為目標函數，優化了薄膜邊界圓弧段跨數和圓心角。2010年，汪有偉等［7］研究了索張力與邊界弧長數目奇偶性質的關系，當膜面邊界跨數為奇數時，支撐結構上的軸力相對較小，結構更加合理。2014年，劉充等人［8］用多區域法研究了圓弧邊界薄膜結構的固有頻率，分析了圓弧花瓣狀薄膜固有頻率與邊界幾何參數的變化關系。

2008年，加拿大航天局Wang等［9］在研究對角張力對方形膜褶皺的影響時發現薄膜邊界附近位移較大的區域呈半橢圓形狀，且該區域內應力很小。Wang等［10］還研究了兩點張拉情況下膜面各點的應力分布，受力點之間的區域應力值較小，形狀近似為半橢圓，且褶皺將發生在此附近，因此作者剪掉小應力，大變形的區域設計了一個半橢圓邊界薄膜裝置。2009年，Guyla［11］從理論上證明了橢圓形薄膜邊界的成立，給出了保持橢圓形邊界上所有應變均為正值曲線垂跨比與薄膜泊松比應滿足的關系，為橢圓形薄膜邊界工程化打下理論基礎。2012年，針對文獻［10］中的平面薄膜裝置，Ryan等［12］使用一種PI控制器消除了薄膜上因為承受熱載荷熱產生的褶皺，這說明熱載荷對平面薄膜天線褶皺的影響不可忽視。

目前對薄膜邊界形狀的研究存在三點不足：首先，僅在承受機械荷載的情況下確立薄膜邊界形狀，沒有考慮天線器件熱對薄膜邊界形狀的影響；其次，對薄膜邊界形狀的研究具有很大局限性，均針對特定的邊界形狀展開，如拋物線等；這些形狀的薄膜受到張拉后，邊界將發生變形，導致實際形狀與預設形狀不一致；最后，學者將薄膜承受的張力作為一個確定的載荷，沒有考慮到結構產生的張力偏差，與實際情況不一致。這些對高精度的天線結構分析都將產生一定的誤差。

針對以上問題，本文考慮了天線單元發熱的情況，且將索張力作為一定變化范圍內的擾動力處理，基于索張力的不確定性，視索膜邊界為樣條曲線，以曲線控制點位移作為設計變量，通過優化索膜結構實際應力與參考應力之間的偏差，對任意邊界薄膜的形狀進行優化，以突破特定邊界形狀的局限。

2 平面薄膜天線有限元建模

平面薄膜天線結構如圖1所示，牽連索和內懸索組成的張拉系統通過管道張拉方式［3］將薄膜懸掛在剛架上，天線陣列單元貼在薄膜表面。

將平面薄膜天線單元發熱等效為一個二維穩態熱平衡問題，認為溫度對薄膜的作用為面內力，則薄膜的溫度分布T僅為坐標x，y的函數，如式（1）所示：

且滿足二維穩態熱平衡方程，即公式（2）：

其中：K為薄膜導熱系數；δ為薄膜厚度；h為薄膜等效換熱系數；T∞為環境溫度；Qi為等i個效熱源。

天線單元產生局部的器件熱，熱源附近的區域發生熱膨脹，而其他地方卻不會，由此導致薄膜各處收縮或者膨脹程度不一致，相互約束產生熱應力，造成膜內應力分布不均勻。在索張力的共同作用下，不合適的張拉將導致褶皺的產生，影響形面精度，制約天線的性能?；诒∧ぞ哂形⑿】箯潉偠鹊奈锢硇再|，本文將膜面視為薄殼結構，內懸索和牽連索視為桿件單元，在內懸索與薄膜重合節點之間建立兩個長度為零的單自由度彈簧單元來模擬索膜的滑動作用，天線陣列單元等效為恒溫熱源。針對圖1所示平面薄膜天線結構，在ANSYS軟件中用平面單元shell57和熱傳導單元link33建立有限元熱分析模型，用殼單元shell181和桿單元link10建立有限元結構分析模型，為提高計算精度，采用shell181單元非協調的完全積分。此時，單元不會產生任何偽機械能，具有很高的精度。將熱分析得到的薄膜結構溫度場作為面內載荷施加到結構模型上，索張力通過給link10單元施加預應變實施。為保證單元之間的正確映射關系，結構模型與熱模型共用一套網格，索膜滑動作用通過彈簧單元combin14模擬。

3 平面薄膜天線邊界形狀優化

本文采用B樣條曲線建立薄膜邊界，以控制點qi的位移量Pi（i＝1，2，…，N）作為設計變量，計算模型和樣條曲線形狀變化情況參見圖2。

假設薄膜邊界由L段樣條曲線組成，每段樣條曲線M取個控制點，每個控制點賦予兩個自由度（x，y），則邊界形狀優化的設計變量數N＝L× 2M，曲線形狀隨控制點位置發生變化，圖2中實線表示曲線初始形狀，垂跨比λ＝h／l，a、b及qi為樣條曲線控制點。虛線表示優化后可能出現的控制點位置以及薄膜邊界曲線形狀。

傳統的天線結構大多以RMS或平面度作為優化目標，而薄膜抗彎剛度小、質量輕，需依靠懸索張拉展開，而不合適的張力易引起膜面應力分布不均，導致褶皺的產生，降低膜面精度，且長期處于高應力狀態容易降低材料使用壽命。綜合考慮膜面應力均勻性和材料使用壽命的影響，膜面應力應盡可能接近工程參考應力值。在工程實踐中，受裝置誤差或其它擾動因素的影響，牽連索拉力具有不確定性，無法達到理想的無偏差拉力，故本文Pi為設計變量，基于索張力的不確定性，以索膜結構真實應力與參考應力值之間的偏差為目標函數，尋求最優邊界形狀。流程圖見圖3。

記懸索單元數為m，薄膜單元數為n，薄膜單元的參考應力值為，單元真實應力值為，索單元的參考應力值為單元真實應力值為，薄膜和索單元的應力偏差權因子分別為ω1和ω2。各約束條件如下：

1）薄膜應力不超過材料容許應力［σ］mem；

2）拉索應力不超過材料容許應力［σ］cab；

3）結構基頻不低于給定值f0；

4）控制點位移最小值為Pl；

5）控制點位移最大值為Pu；

6）索張力最小值為Fmin；

7）索張力最大值Fmax。

索膜應力數據和基頻可通過有限元熱——結構耦合分析得到。

由圖3可知最小應力偏差設計的數學模型為嵌套優化模型，優化模型由外層優化Ⅰ和內層優化Ⅱ構成。

外層優化Ⅰ：將內層優化得到的索張力視為確定力，找到懸索和膜面應力偏差最小情況下的控制點位移Pi，優化模型如式（3）～（9）所示：

內層優化Ⅱ：基于牽連索拉力不確定性，找到內懸索和膜面應力偏差最大情況下的一組索張力，優化模型如式（10）～（16）所示：

式中：Pi是第i個控制點位移量；

［σ］mem為薄膜材料容許應力；

［σ］cab為懸索材料容許應力；為膜面參考應力值；

f0為給定結構基頻；

Pl為控制點位移的最小值；

Pu為控制點位移的最大值；

Fj為第j個牽連索拉力；

Fmin牽連索拉力的最小值；

Fmax牽連索拉力的最大值。

對以上嵌套優化數學模型采用序列二次規劃法求解，即對目標函數做二次泰勒展開，對約束條件做一次泰勒展開，并用變尺度法構造目標函數的Hessen陣，上述優化模型可寫作式（17）～（30）：

其中：

pk為優化過程中第k次迭代的設計變量；

δPk＝[δP1，δP2，…δPN]表示設計變量在pk處的增量，記為；為薄膜單元應力約束函數在Pk處的梯度向量；

本文的優化模型適用于不確定索張力條件下任意形狀的薄膜邊界，突破了特定邊界形狀的限制。

4 算例仿真

圖4所示為平面薄膜天線，薄膜中心印有一個2 cm×2 cm的天線單元，邊界由16段相同的三次B樣條曲線組成，每段樣條曲線跨度固定為0? 25 m，控制點數目為5個。

曲線兩端點a、b固定，為保證結構對稱性并減小計算量，本文將其余48個控制點位移Pi歸并為兩類：第一類控制點為曲線頂點qi1；第二類為位于曲線頂點和固定點之間的控制點qi2，qi2關于曲線對稱軸對稱；兩類控制點都僅具有徑向自由度，其徑向位移分別表示為Pi1＝P1，pi2＝P2。

為驗證本文提出的邊界形狀優化方法的有效性，分別進行了如下兩個算例的仿真校驗。

4? 1 平面薄膜天線熱應力仿真校驗

本文基于圖4所示模型進行了熱應力計算的數值仿真。薄膜中心天線單元等效為60℃的恒溫熱源，不考慮天線單元與外層空間的熱輻射，為平衡輻射散熱對膜面溫度場分布的影響，增大膜面的對流作用，取對流換熱系數為10，環境溫度為25℃。周邊懸索四個角點處張力為7 N，其他懸索張力為5 N。索膜結構材料參數如表1所示。

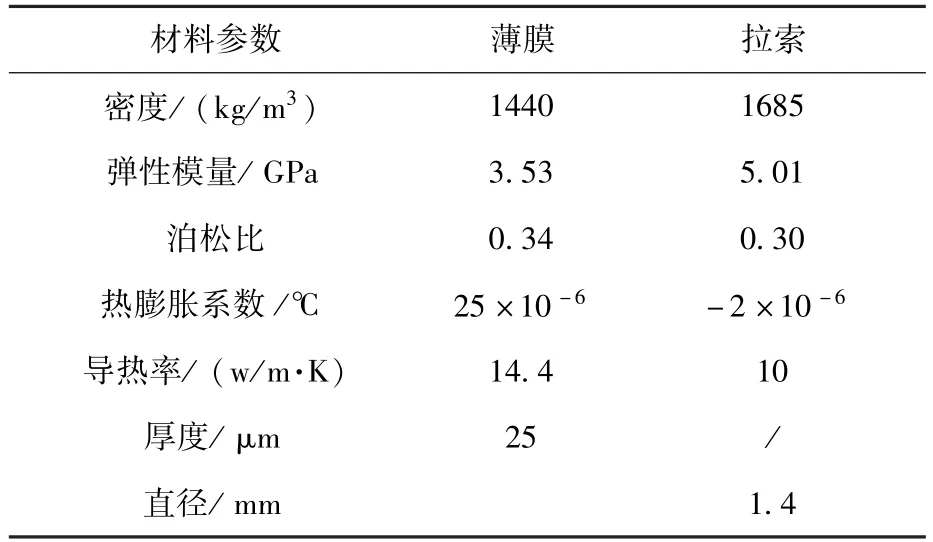
表1 索膜結構材料參數Table 1 Material parameters of the planar membrane antenna

根據二維線彈性熱平衡，穩定熱分析結果如圖5所示。

由圖5可知膜面溫度受天線發熱影響較大，熱量以熱源為中心向周圍傳遞，溫度從膜面中心到邊界逐步降低。熱載荷和索張力共同作用下的平面薄膜天線第二主應力云圖如圖6所示。若不考慮天線單元發熱對薄膜應力均勻性的影響，索張力作用下的無熱源平面薄膜天線第二主應力云圖如圖7所示。

對比圖6、圖7可知，天線單元發熱對膜面應力分布影響很大。不考慮熱源的平面薄膜天線，薄膜第二主應力的極大值出現在薄膜中心，邊界處應力值相對較小，且結構應力均為正值；考慮天線單元的熱效應后，薄膜第二主應力云圖發生明顯變化。應力值總體由薄膜中心區域向邊界遞增，中心區域應力值最小，出現負值，邊界應力值最大。這是因為薄膜中心區域離熱源比較近，溫度變化明顯，天線單元發熱產生的熱應力占主導作用，而薄膜邊界離熱源較遠，溫度變化不明顯，索張力占主導作用。

本文提取膜面應力數據對兩種工況下的薄膜進行對比，如表2所示。

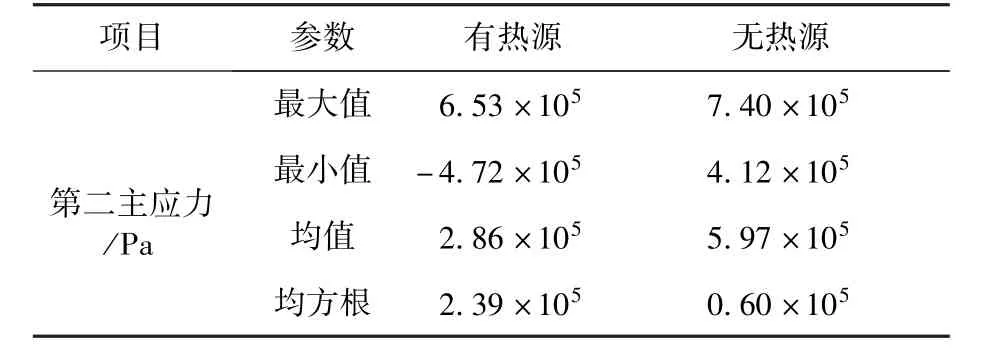
表2 薄膜第二主應力結果對比Table 2 The second principal stresses of membrane

考慮天線單元的熱應力后，薄單元第二主應力最大值、最小值和均值都減小，應力均方根較無熱源的薄膜大，高出一個數量級?？梢娞炀€單元的熱效應會使得膜面應力分布不均勻，薄膜抗彎剛度小，膜面應力分布不均勻會嚴重影響膜面精度。不考慮熱應力的膜面應力與真實膜面應力差別明顯，基于這種應力狀態下設計的邊界形狀不適用于實際情況下的薄膜天線，薄膜邊界形狀的研究應該考慮熱應力的影響。

4? 2 薄膜邊界形狀優化算例

針對圖4所示薄膜天線，首先，在牽連索為理想的無偏差拉力的工況下，對薄膜邊界形狀進行優化，得到理想狀態最優邊界形狀，然后，考慮工程實際中牽連索受結構裝置或外界擾動等因素影響，張力具有不確定性的特點，進一步在拉力不確定的兩種工況下，對平面薄膜邊界形狀進行優化。

工況一：理想狀態下，索張力無偏差，薄膜均勻受拉，角點處索張力為7 N，其他位置索張力為5 N，如圖8所示。

工況二：基于索張力不確定性，根據對稱性質，將不確定索張力歸為3類，如圖9所示。中點處懸索張力為F1，中點兩側懸索張力記作F2，角點處懸索張力記作F3，張力具有不確定性，偏差范圍為5%。

工況三：基于索張力不確定性，將16個牽連索拉力分為16個拉力變量，分別表示為F1、F2、…、F16，張力偏差范圍為5%，如圖10所示。

以初始形狀下的控制點位置為基準，當控制點沿徑向向薄膜對稱中心移動時，位移為正，反之為負。薄膜初始預應力為1? 4 MPa，初始索張力為圖8所示。取初始控制點垂跨比為λ＝0．132，基頻不低于0? 06 Hz。兩類控制點移動范圍均為［－15 mm，16 mm］，設定薄膜參考應力值為0? 31 MPa，內懸索參考應力值為1? 81 MPa。由于薄膜單元數量遠大于索單元，為平衡兩部分應力偏差所占目標函數的權重，取薄膜應力偏差權因子ω1＝0．3，懸索應力偏差權因子ω2＝0．7，分別對以上三種模型進行優化。

表3為優化結果，由表3可知，經過優化后平面薄膜天線結構基頻幾乎不變。采用彈簧單元模擬索膜之間的相互滑移，結構受拉之后，索膜之間產生很小的相對位移，幾乎可以忽略。工況一下的平面薄膜天線，由于其承受無偏差索張力，索膜結構單元應力偏差較小，目標函數值由1．81×106Pa降到218 Pa，下降幅度達99? 9%，第一類控制點位移P1由－4? 00 mm變為5? 00 mm，第二類控制點位移P2由－5? 00 mm變為6? 00 mm?？紤]實際索張力與理想情況的偏差范圍后，索張力為一組在5 ×［0? 95，1? 05］內的任意數值，目標函數值要大于無偏差索張力情況下的值，工況二索膜應力偏差下降幅值達到99? 2%，工況三索膜應力偏差下降幅值達到99? 6%。這是因為索張力在偏差范圍內變動，使得薄膜結構應力數據改變，與無偏差索張力薄膜應力數據存在一定誤差。

表3 薄膜天線邊界形狀優化結果Table 3 Results of boundary shape optimization of thin film antenna

三種工況下優化得到的薄膜邊界形狀相差不大，工況三較為接近工程實際，相較于其他兩種工況更具有參考意義，薄膜初始形狀及工況三下的薄膜優化形狀對比如圖11所示。

在平面薄膜陣天線的有限元模型中截取一段具有代表性的邊界曲線（如紅色框），圖中點1、2、3、4、5組成的藍色曲線為初始形狀，點1、6、7、8、5組成的紅色曲線為工況三優化得到的最優邊界形狀。其中，點1、5為固定點，點3、7為第一類曲線控制點，點2、4、6、8為第二類曲線控制點。在索張力偏差5%的干擾下，曲線控制點2、4沿徑向向薄膜中心平移到點6和點8的位置，移動距離為8? 53 mm；曲線控制點3移動到點7的位置，移動距離為10? 83 mm。與初始形狀相比，最優邊界形狀垂跨比增大。

通過優化，在提高膜面精度的同時極大地增加了膜面應力均勻性，優化效果十分顯著，考慮牽連索拉力不確定性的優化是為了提高結構的穩健性，優化結果驗證了該方法的有效性。

5 結論

1）本文采用三次B樣條曲線作為薄膜邊界形狀，以曲線控制點位移為設計變量，通過優化實際結構索膜應力與參考應力偏差，突破了特定邊界形狀的限制，實現了對薄膜邊界形狀的優化。

2）本文提出的平面薄膜邊界形狀優化方法考慮了天線單元的熱效應和索張力偏差對薄膜邊界應力均勻性的影響，與實際工程更為接近，適用于任意邊界形狀的薄膜，對薄膜邊界形狀設計提供了一定的參考。

（References）

［1］ 杜星文，王長國，萬志敏．空間薄膜結構的褶皺進展研究［J］．力學進展，2006，36（2）：187?199 Du Xingwen，Wang Changguo，Wan Zhimin．Study on the?wrinkle of the space membrane structures［J］．ADVANCES IN MECHANICS，2006，36（2）：187?199．（in Chinese）

［2］ 肖薇薇，陳務軍，付功義．空間薄膜陣面結構褶皺分析［J］．宇航學報，2010，31（11）：2604?2609．Xiao Weiwei，Chen Wujun，Fu Gongyi．Wrinkle analysis for space planar filmreflect?array［J］．Journal of Astronautics，2010，31（11）：2604?2609．（in Chinese）

［3］ Fang H，Lou M，Hsia L，et al．Catenary systems for mem?brane structures［R］．AIAA?2001?1342，2001．

［4］ Greschik G，White C V，Salama M A．On the precisely uni?form and uniaxial tensioning of a film sheet via integrated cate?nary［J］．AIAA?2003?1096，2003．

［5］ Heald J C，Potvin M J，Jiang X X．Experimental investiga?tions to support a multi?layer deployable membrane structure for space antennae［R］．AIAA?2005?2317，2005．

［6］ Hiraku Sakamoto．Dynamic Wrinkle Reduction Strategies for Membrane Structures［D］．Colorado：University of Colorado，2004．

［7］ 汪有偉，關富玲，韓克良．內外部懸索聯合張拉膜結構的設計與分析［J］．浙江大學學報（工學版），2010，44（6）：1213?1319．WANG Youwei，GUAN Fuling，HAN Keliang．Design and a?nalysis of inner and outer cables suspended membrane struc?tures［J］．Journal of Zhejiang University（Engineering Sci?ence），2010，44（6）：1213?1319．（in Chinese）

［8］ 劉充，李玉宇，保宏．邊界幾何參數對空間平面張拉膜結構固有頻率影響研究［J］．振動與沖擊，2014，34（20）：198?202．Liu Chong，Li Yuyu，Bao Hong．The natural frequencies of?pre?tensioned membrane structure with different boundary geo?metrical parameters［J］．Journal of vibration and shock，2014，34（20）：198?202．（in Chinese）

［9］ Wang X，Sulik C，Zheng W，et al．High?fidelity wrinkling analysis of membrane structures and elliptical cut optimization［R］．AIAA?2008?2255，2008．

［10］ Wang X，Zheng W，Hu Y R．Active flatness control of space membrane structures using discrete boundary SMA actuators［C］／／Advanced Intelligent Mechatronics，2008．AIM 2008．IEEE／ASME International Conference on．IEEE，2008：1108?1113．

［11］ Greschik G．Mechanically Seamless Catenary Edge Support for Orthotropically Stretched Membranes［R］．AIAA?2009?2161，2009．

［12］ Orszulik R，Shan J．A Simple PI Controller for Active Flat?ness and Tracking Control of a Space Membrane Structure［R］．AIAA?2012?1920，2012．

（責任編輯：康金蘭）

Boundary Shape Optimization of Planar Membrane Antenna Based on Thermal Load and Cable Tension

HE Qun1，BAO Hong1?，DU Jingli1，PENG Fujun2
（1．Key Laboratory of Electronic Equipment Structure Design，Ministry of Education，Xidian University，Xi’an 710071，China；2．Aerospace Systems Engineering Shanghai，Shanghai 201108，China）

The planar membrane phased array antenna is adversely affected by the heat of various device and the uncertain cable tension．A boundary shape optimization method for the planar mem?brane phased array antenna was proposed in this paper．First，considering the thermal effect of the antenna element，the thermo?mechanical Finite Element Analysis model of the planar membrane an?tenna was established．Then based on the cable tension uncertainty，and taking the membrane boundary as a cubic B?spline curve，the optimization model was established with the control point displacement as the design variable．By optimizing the deviation of the actual structural stress and the reference stress，the suitable membrane boundary shape was obtained．In the end，the validity of the proposed method was verified by numerical simulation．Compared with the current membrane boundary shape optimization，the proposed method can achieve any arbitrary curve optimization．

planar membrane antenna；device heat；cable tension combination；boundary shape op?timization

TN957? 2

A

1674?5825（2017）04?0454?08

2017?03?01；

2017?06?30

國家自然基金重大計劃（51490660）；國家自然科學基金（51675398）；上海航天科技創新基金（SAST201413）

賀群，女，碩士研究生，研究方向為結構與控制的一體化設計。E?mail：hq＿hcw＠163．com

?通訊作者：保宏，男，博士，研究方向為電子裝備結構設計與精密控制。E?mail：hbao＠xidian．edu．cn