基于驅動機構作動的柔性附件振動控制原理與算法

李 濤，陳必發，呂亮亮，唐國安，?

·柔性結構機構動力學與控制·

基于驅動機構作動的柔性附件振動控制原理與算法

李 濤1，陳必發1，呂亮亮2，唐國安1，2?

（1．復旦大學航空航天系，上海200433；2．上海宇航系統工程研究所，上海201108）

針對空間飛行器柔性附件低頻振動衰減緩慢降低系統穩定性和可靠性的問題，以帶有驅動機構的太陽能電池翼為例，不增加額外機構，提出了以驅動機構為作動器、電池翼與驅動機構約束扭矩為目標的振動控制方法。推導了模態坐標表示的電池翼振動的狀態方程，選擇第一階模態描述電池翼彎曲振動并設計反饋控制律。以鋼質彈性直尺為模型，通過數值仿真驗證了該方法的有效性。

振動控制；電池翼；模態坐標；反饋控制

1 引言

太陽能電池翼是航天器上由太陽能電池片、太陽能電池基板、展開機構、鎖定機構、驅動機構等組成的重要裝置。當航天器入軌后，鎖定機構釋放，由板間鉸鏈內的扭簧驅動，最終展成一個平面，其作用是吸收太陽的輻射能并將其轉化成電能，為航天器提供能源［1］。

如今，各國航天器的發展呈現出大型化趨勢，大型太陽能電池翼能夠為航天器提供足夠的能源供給。但是，這些轉變也給航天器結構的設計及安全運行帶來了一系列新的挑戰［2］。相對于航天器本體，太陽電池翼的柔性較大、阻尼比很小，致使其在定向、調姿、變軌等過程中被激起的振動頻率低，衰減緩慢。這些振動不僅影響航天器的姿態穩定度、定位精度以及有效載荷的正常工作，嚴重時還會降低航天器的使用壽命甚至導致其結構破壞［3］，因此有必要采取有效措施對太陽翼的殘余振動進行抑制。

有關太陽翼在航天器變軌過程中的減振研究表明：傳統的被動振動控制方法具有結構簡單、易于實現、經濟性良好等優點，是較早使用的振動抑制方法，這種方式需要使用額外硬件，對振動進行機械隔離或者通過能量消耗的方式衰減振動。其采用的裝置通常包括彈性阻尼元件和彈性元件等［4］。但受結構質量、材料性能等因素的制約，減振效果不易達到太陽能電池翼振動控制的嚴苛要求［5］。那帥、朱春艷等將輸入整形技術應用于抑制太陽翼調姿后的殘余振動，利用驅動機構現有的硬件、無需增加其他附件，將初始參考指令與一系列脈沖序列卷積生成整形指令作為輸入信號，取得了不錯效果［6?8］。有學者采用開關式噴射發動機、運用不同的開關策略來實現振動抑制［9］，但作動需要消耗工質，不宜頻繁采用。應用壓電陶瓷、壓電聚合物等壓電材料為作動器的主動控制技術發展迅速，控制效果顯著［10?15］。但這類方法需要復雜的理論推導和嚴苛的控制條件，控制器的參數設計存在不少經驗因素。航天器太陽電池翼通常自備驅動機構，用于調整太陽帆姿態實現其對日定向。鑒于驅動機構輸出功率大又不消耗工質的特點，將其作為振動控制的作動器，對航天器而言，不增加額外的非有效質量，因此，對其原理和算法值得進行探索和研究。

2 驅動機構作動的電池翼控制方程

為簡化考慮，在分析電池翼振動時將航天器本體視為靜止體。圖1所示為一航天器太陽翼簡化模型。以太陽翼根部為原點、延伸方向為Z軸、垂直于太陽翼面方向為X軸，根據右手定則在太陽翼上建立隨驅動機構運動的直角坐標系O－XYZ。當驅動機構作用時，該坐標系繞Y軸轉動，轉動角度等于驅動角，記為α。

對于大型太陽能電池翼來說，其振動主要發生在低階彎曲模態，因此將控制對象鎖定為太陽翼在YOZ平面內的橫向彎曲振動，控制量為調姿驅動器沿Y軸轉動的角加速度α¨。

電池翼受激勵后發生振動，參考該坐標系的相對位移記為xr。由于參考坐標系是非慣性坐標系，應用達朗貝爾原理可以列出電池翼的運動方程如式（1）：

式中，M、C、K分別為太陽能電池翼有限元模型的質量陣、阻尼陣和剛度陣，xr＝｛x1x2…xn｝T為節點位移向量，f（t）為慣性力。

設太陽翼繞驅動點轉動的剛體約束模態為Ψ，當轉動角加速度為α¨時，太陽翼上各處的加速度為α¨Ψ，則慣性力可表示為式（2）：

將其代入方程（1）可得式（3）：在線性變形范圍內，驅動機構的彎矩正比于電池翼的相對位移，可寫成式（4）：

選取若干太陽翼根部固支的固定界面主模態Φ，將位移向量xr表示為式（5）：

然后代入方程（3），并在方程兩端同時乘以矩陣ΦT，根據模態的正交性，可以得到式（6）：

其中各變量符合式（7）：

彎矩表達式（4）則變為式（8）：

將式（6）表達為式（9）所示狀態空間的形式：

其中各變量符合式（10）：

式（6）為解耦的系統模態運動方程，其第i階方程可表示為式（11）：

對于大型太陽翼而言，其大幅振動主要由第一階模態振動構成，故可取i＝1來研究太陽翼系統的振動控制問題。

3 控制律的設計

太陽翼第一階振動的模態運動方程為式（12）：

式（12）右端為驅動結構的輸入扭矩，可表示為式（13）：

其中ζa為人工阻尼系數。此時式（12）可寫為式（14）：

根據式（14），在小阻尼情況下，人工阻尼ζa越大，太陽翼振動衰減越快。

相較于驅動機構的角加速度α¨，其角速度α·的控制更容易實現。將式（13）兩端積分得式（15）：

記驅動機構的轉速為式（16）：

由公式（8），僅考慮一階模態時，太陽翼根部即1號節點處彎矩可表示為式（17）：

結合（15）、（17），驅動機構轉速與彎矩之間有式（18）所示關系：

4 仿真算例的驗證

為了驗證該振動控制方法的有效性，考慮到圖1太陽翼模型結構的對稱性，將其簡化為圖2所示帶配重的鋼尺。鋼尺截面為40×2（mm）的矩形，左端固定，安裝了m1、m2兩個配重，楊氏模量E＝2．1×1011Pa，密度ρ＝7．8×103kg／m3，泊松比ν＝0．3。設定一階模態阻尼比ζ1＝0? 002 3，由Nastran算得鋼尺第一階固有頻率ω1＝4? 8406 rad／s。

仿真共設計了兩種工況。其中工況1給定鋼尺末端初始位移，模擬地面實驗狀況；工況2驅動機構作動作為初始激勵，模擬太陽能電池翼在軌調姿過程后的殘余振動。在此基礎上，利用MATLAB進行仿真。

工況1中，給定鋼尺末端0? 1 m形變作為初始位移，根據公式（18），考慮到驅動機構的最大轉速能力，設定控制增益β＝Ωmax／Tzmax＝0? 052 9。鋼尺根部約束彎矩隨時間變化的曲線如圖3所示，結果表明實施控制加速了振動的衰減。

為驗證控制增益對振動抑制效果的影響，選取4組不同的增益，等效為4組人工阻尼系數，其中第1組設置增益為0，根據式（18），相當于驅動機構轉速Ω為零，不加控制，仿真結果見圖4。

記錄振動衰減到最大振幅5%所用的時間，見表1。

表1 不同增益下衰減時間及最大驅動轉速Table 1 Attenuation time and maximum driving rota?tional speed with different control gains

由表1可知，隨著控制增益增大，等效的人工阻尼系數相應增大，鋼尺振動幅度衰減到低于最大振幅5%所用的時間依次減少為19? 5 s、10? 4 s、7? 8 s，相較于不加控制時需要268? 69 s，時間依次縮短為原來的7? 26%、3? 87%和2? 9%，與理論分析一致。同時，隨著控制增益的增大，所需要的驅動機構的最大轉速也在提高。因此，應根據驅動機構轉速的最大能力來選擇相應的增益系數。

工況2利用驅動機構作動，采用梯形信號輸入，初始1? 28 s內驅動機構轉速Ω如圖5所示。

實施控制前后，鋼尺根部約束彎矩隨時間變化的曲線如圖6所示，結果表明實施控制加速了振動衰減，效果顯著。

同樣，為驗證控制增益對振動抑制效果的影響，選取4組不同的增益也即4組人工阻尼系數見表2，第一組增益設置為0，根據式（18），相當于驅動機構轉速Ω為0，不加控制，仿真結果見圖7。

記錄振動衰減到最大振幅5%所用的時間，見表2。

由表2可知，隨著控制增益增大，等效的人工阻尼系數相應增大，鋼尺振動幅度衰減到低于最大振幅5%所用的時間依次減少為9? 49 s、4? 42 s、3? 11 s，相較于不加控制時需要266? 44 s，時間依次縮短為原來的3? 56%、1? 66%和1? 17%。同樣，隨著控制增益的增大，所需要的驅動機構的最大轉速也在提高。因此，應根據驅動機構轉速的最大能力來選擇相應的增益系數。

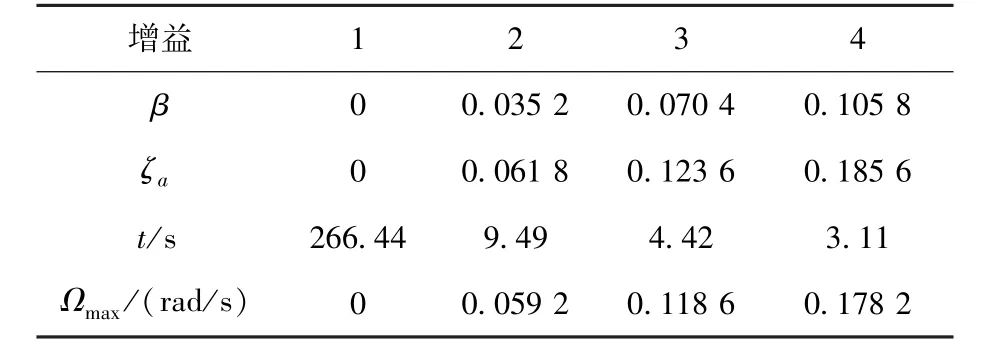
表2 不同增益下衰減時間及最大驅動轉速Table 2 Attenuation time and maximum driving rota?tional speed with different control gains

5 結論

針對航天器柔性附件的振動問題，結合計算機仿真，實現了以驅動機構為作動器的振動控制方法，仿真結果表明：

1）基于驅動機構作動的柔性附件振動控制方法能產生明顯的減振效果；

2）在小阻尼情況下，控制增益越大，等效的人工阻尼系數越大，振動衰減的速率越快。

（References）

［1］ 袁家軍．衛星結構設計與分析［M］．北京：中國宇航出版社，2004．Yuan Jiajun．Design and Analysis of Satellite Structure［M］．Beijing：China Aerospace Press，2004．（in Chinese）

［2］ 黃文虎，王心清．航天柔性結構振動控制的若干新進展［J］．力學進展，1997，27（1）：5?18．Huang Wenhu，Wang Xinqing．Recent advances in vibration control of flexible structures［J］．Advances in Mechanics，1997，27（1）：5?18．（in Chinese）

［3］ 李東旭．撓性航天器結構動力學［M］．北京：科學出版社，2010．Li Dongxu．Structural Dynamics of Flexible Spacecraft［M］．Beijing：Science Press，2010．（in Chinese）

［4］ 許雲淞．撓性衛星姿態機動及太陽帆板振動抑制研究［D］．哈爾濱：哈爾濱工業大學，2014．Xu Yunsong．Research on Attitude Control and Solar Array Vibration suppression of a Flexible Satellite［D］．Harbin：Harbin Institute of Technology，2014．（in Chinese）

［5］ Maly J R．Hubble space telescope solar array damper［C］／／1999 Symposium on Smart Structures and Materials．Interna?tional Society for Optics and Photonics，1999：186?197．

［6］ 那帥，朱春艷，彭福軍，等．基于輸入整形技術的太陽翼調姿殘余振動抑制實驗研究［J］．振動與沖擊，2013，32（7）：107?112．Na Shuai，Zhu Chunyan，Peng Fujun，et al．Test for residual vibration suppression of a solar array during attitude control based on input shaping technique［J］．Journal of Vibration and Shock，2013，32（7）：107?112．（in Chinese）

［7］ 朱春艷，邵濟明，那帥，等．太陽電池翼調姿后殘余振動抑制的整形器設計［J］．振動與沖擊，2012，31（8）：176?180．Zhu Chunyan，Shao Jiming，Na Shuai，et al．Design and simulation of input shaper for residual vibration suppression after attitude adjustment of a solar array［J］．Journal of Vibra?tion and Shock，2012，31（8）：176?180．（in Chinese）

［8］ 朱春艷，紹濟明，唐國安．雙輸入整形器抑制兩軸轉動太陽翼調姿后的殘余振動［J］．噪聲與振動控制，2011，32（6）：1?4．Zhu Chunyan，Shao Jiming，Tang Guoan．Design and simula?tion ofdouble?input shaper for suppressing residual vibration after attitude adjustment of solar array［J］．Noise and Vibra?tion Control，2011，32（6）：1?4．（in Chinese）

［9］ 任萱．人造地球衛星軌道力學［M］．長沙：國防科技大學出版社，1988．Ren Xuan．Orbital Mechanics of Artificial Earth Satellite［M］．Changsha：National Defense Science and Technology University Press，1988．（in Chinese）

［10］ Meyer J L，Harrington W B，Agrawal B N，et al．Vibration suppression of a spacecraft flexible appendage using smart ma?terial［J］．Smart Materials＆Structures，1998，7（1）：95．

［11］ Song G，Agrawal B N．Vibration suppression of flexible spacecraft during attitude control［J］．Acta Astronautica，2001，49（2）：73?83．

［12］ Hu Q，Ma G．Spacecraft vibration suppression using variable structure output feedback control and smart materials［J］．Journal of Vibration＆Acoustics，2006，128（2）：221?230．

［13］ Sales T P，Rade D A，Souza L C G D．Passive vibration con?trol of flexible spacecraft using shunted piezoelectric transduc?ers［J］．Aerospace Science＆Technology，2013，29（1）：403?412．

［14］ Wu D，Huang L，Pan B，et al．Experimental study and nu?merical simulation of active vibration control of a highly flexi?ble beam using piezoelectric intelligent material［J］．Aero?space Science＆Technology，2014，37：10?19．

［15］ Hardy S M，Lindgren M，Konakanchi H，et al．Decentralized vibration control of a multi?link flexible robotic manipulator u?sing smart piezoelectric transducers［J］．Acta Astronautica，2014，104（1）：186?196．

（責任編輯：龍晉偉）

Principle and Algorithm of Vibration Control in Flexible Appendage Based on Actuating Mechanism

LI Tao1，CHEN Bifa1，LV Liangliang2，TANG Guoan1，2?
（1．Department of Aeronautics and Astronautics Fudan University，Shanghai 200433，China；2．Shanghai Institute of Aerospace System Engineering，Shanghai 201108，China）

The flexible appendage of a spacecraft usually has the feature of low rigidity and damping，and the slow attenuation of the low?frequency vibration may reduce the stability and reliability of the aircraft system．To solve the vibration problem of the spacecraft flexible appendage，the solar battery wings with driving mechanism was taken as an example and a vibration control method was proposed without adding any additional mechanism．The driving mechanism was used as the actuator and the constraint moment of the wings and driving mechanism was controlled．The state equation of the vibra?tion of the battery wings was derived by the modal coordinates．The first order mode was used to de?scribe the vibration of the battery wings and the feedback control law was developed．The effectiveness of the method was verified by numerical simulation with the steel elastic ruler as the model．

vibration control；battery wings；modal coordinates；feedback control

O328

A

1674?5825（2017）04?0482?05

2017?01?18；

2017?06?12

國家自然科學基金（11572089）

李濤，男，碩士研究生，研究方向為結構動力學與振動控制。E?mail：taoli15＠fudan．edu．cn

?通訊作者：唐國安，男，碩士，教授，研究方向為動力學與控制。Email：tangguoan＠fudan．edu．cn