淺談小學數學教學中幾何直觀能力的培養
趙惠卿

摘 要:幾何直觀所指有兩點:一是幾何,在這里幾何是指圖形;二是直觀,這里的直觀不僅僅是指直接看到的東西(直接看到的是一個層次),更重要的是依托現在看到的東西、以前看到的東西進行思考、想象,綜合起來,幾何直觀就是依托、利用圖形進行數學的思考和想象。它在本質上是一種通過圖形所展開的想象能力。
關鍵詞:小學生;數學;幾何直觀能力
作為一線教師,我們應全面理解幾何教育價值,重視對學生幾何直觀能力的培養。那么,在教學中如何培養學生的幾何直觀能力呢?
一、在日常學習中逐步培養學生畫圖的習慣
在日常教學中,幫助學生養成畫圖的習慣是非常重要的。可以通過多種途徑和方式使學生真正體會到畫圖堆理解概念、尋求解題思路帶來的益處。動手畫圖要從小開始培養,比如一年級上冊練習有這樣的一道題:小紅的前面有3個人,后面有4個人,小紅他們這一組一共有多少人?學生看到這個題目后,列出的算式是:3+4=7(人)。教師在講評中列出算式3+1+4=8(人),強調為什么要加1,因為小紅在這個隊伍中也算一個。學生“哦”一聲,只知道小紅也是一個,要加1,而過段時間后,碰到類似的題目,學生又全部忘了。如果在分析這道題時,我們能借此向學生滲透線段圖,如:
這樣講解以后,學生在遇到類似的題目就會想到用畫圖解決,慢慢就養成了畫圖的習慣了,解題的準確率也提高了。
二、重視變換,讓圖形動起來
幾何變換或圖形的運動是幾何,也是整個數學中很重要的內容,它既是學習的對象,也是認識數學的思想和方法。變換又可以看作運動,讓圖形動起來是指在認識這些圖形時,在頭腦中讓圖形動起來。比如《圓的周長計算公式》,在測量圓的周長時,教師可以鼓勵學生用不同的方式進行測量,如用一塊圓形木板(或硬紙板),用線(或紙條)繞圓一周,量得它的長度。也可以在圓上畫一個點,在直尺上滾動一周直接量出圓的周長。學生用測量的方法量出了這些圓的周長以后,教師可以進一步提出問題:“要是有一個很大的圓,怎么測量它的周長呢?比如圓形花壇。”也許學生會說可以拿測量土地的卷尺繞花壇一周進行測量,教師可以舉出更多的圓的例子,引導學生去尋求更為一般化的方法。在這兒,教材為學生直接指明了研究的方向,即通過測量不同大小的圓的周長和直徑,計算出周長和直徑的比值,使學生發現,不管圓的大小怎么變化,圓的周長總是直徑的三倍多一點。根據圓的周長和直徑的倍數關系,可以得出求圓的周長的計算公式。這樣充分利用變換去認識、理解圓的周長,學生在運用時就會想起公式的由來,對公式的理解就更深刻了。
三、學會畫平面圖分析和解決問題
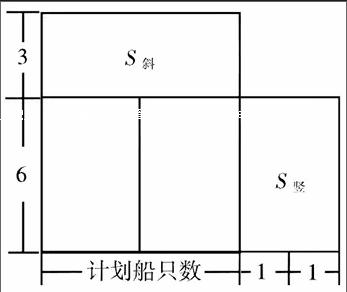
我們學過畫線段圖來分析應用題,這樣做可以使問題具體、形象。但是,在我們解答一些要同時考慮兩個因素的應用題時,如果用長方形的長和寬分別表示兩個不同的因素,畫出長方形來,再利用長方形的面積進行分析,往往更方便一些。長方形圖解應用題主要是“抓住面積不變,借助一個量增加,則另一個量減少”這一基本規則來解決問題。比如,有一個班的學生去劃船,若增加一只船,則每只船剛好坐6人;若減少一只船,則每只船剛好坐9人,該班共有多少人?此題以前我們都是用假設法來解這種題,今天我們試著用長方形圖解(如圖)
用長方形的長表示船只數,用寬表示每船坐的人數。由題意,S斜=S豎,S豎=6×2
6×2÷3=4(只)…(計劃船只數少一只)
9×4=36(人)…總人數
還可以這樣想:S白=2S豎(空白長方形的寬是斜條長方形寬的2倍;長相同),把空白長方形分割成兩個面積相等的長方形,S斜=S豎,總人數可用3S豎來表示:6×2×3=36(人)…總人數。
運用“長方形圖解法”進行教學,來解答類似的應用題,不僅可使題目化難為易,而且能提高學生的解題能力,促進學生思維的發展,有效發展學生的幾何直觀能力。
綜上所述,我們在整個數學教學中重視幾何直觀能力的培養,就能讓幾何直觀在教學中發揮著把復雜的數學問題變得簡明、形象,有助于探索解決問題的思路,預測結果。希望數學教師重視它,在日常教學中幫助學生不斷提升這種能力,讓幾何直觀在學習數學中發揮它應有的重要作用。
參考文獻:
希爾伯特.直觀幾何[M].王聯芳,譯.高等教育出版社,1959.
編輯 魯翠紅endprint

