基于LASSO類方法的Ⅰ類錯誤的控制*

山西醫科大學衛生統計教研室（030001） 許樹紅 王 慧 孫紅衛 王 彤

基于LASSO類方法的Ⅰ類錯誤的控制*

山西醫科大學衛生統計教研室（030001） 許樹紅 王 慧 孫紅衛 王 彤△

全基因組關聯研究（genome-w ide association studies，GWAS）是在全基因組范圍內同時研究上百萬個單核苷酸多態性（single nucleotide polymorphism，SNP）位點與疾病或某些性狀之間的關聯，從而篩選出可能的致病SNP位點，進而對這些位點進行人群驗證和實驗分析。在GWAS研究中比較傳統的分析方法是針對每個SNP和結局變量間關聯進行單因素分析的假設檢驗，而待分析的SNP數量有幾十萬甚至上百萬個，使得檢驗次數十分巨大，如果不采用合適的方法進行多重性校正來妥善控制Ⅰ類錯誤，會產生許多假陽性結果，對這些結果進行驗證將耗費很多時間和財力，造成不必要的損失。針對全基因組測序數據進行多因素建模常采用的分析策略為降維和變量選擇。變量選擇的方法包括經典方法和懲罰類方法，懲罰類方法在GWAS研究、測序數據分析中應用廣泛且發展迅速，它假定模型具有稀疏性即真實情況下許多未知候選變量的回歸系數為0或者接近0，因此自變量的選擇問題轉化為確定正確的子模型問題，且在選擇變量的同時給出模型參數的估計。LASSO（least absolute shrinkage and selection operator）作為一種常用的懲罰類方法，部分研究者指出其選出的變量存在較高的假陽性問題［1-3］。針對該類問題，在多重校正以及變量選擇方法的基礎上，發展了一些控制Ⅰ類錯誤的同時篩選出正確變量的方法。本文主要對多重檢驗中控制Ⅰ類錯誤的方法進行總結并且對基于LASSO的Ⅰ類錯誤的控制方法進行綜述。

多重檢驗中控制Ⅰ類錯誤的策略和方法

經典的多重檢驗校正是建立在多個檢驗之間或P值之間相互獨立的假設上［4］，然而在針對基因數據的多個假設檢驗中得到的P值之間往往是不獨立的，目前處理這種不獨立情況的方法大致分為三類：第一種是不做任何假設；第二種是假設P值之間存在PDS假設（positive dependence through stochastic ordering，PDS）［5-7］，PDS假設有弱PDS假設和強PDS假設兩種，前者為：對每一個成立的H0對應的P值qi，及所有qi的不減函數f，在qi＝u的條件下，E [f（q1，…，qm0）｜qi＝u]是不減的，后者為：對每一個H0對應的P值pi及其不減函數f，在qi＝u的條件下，E [f（p1，…，pm）｜qi＝u]是不減的；第三種是基于排列抽樣的方法。目前常用的控制Ⅰ類錯誤的方法有兩大類，分別是控制FWER（family-w ise error rate，FWER）和控制FDR（false discovery rate，FDR）。

設進行m次假設檢驗，原假設為H0，i，i＝1，…，m，對應的P值表示為pi，i＝1，…，m。將成立的H0對應的P值定義為qi，i＝1，…，m0。表1是各種可能的檢驗結果，m0和m1分別是檢驗中成立的H0及不成立的H0的個數。V是檢驗中成立的H0被錯誤拒絕的個數。π0＝m0／m，是m次假設檢驗中成立的H0所占比例。

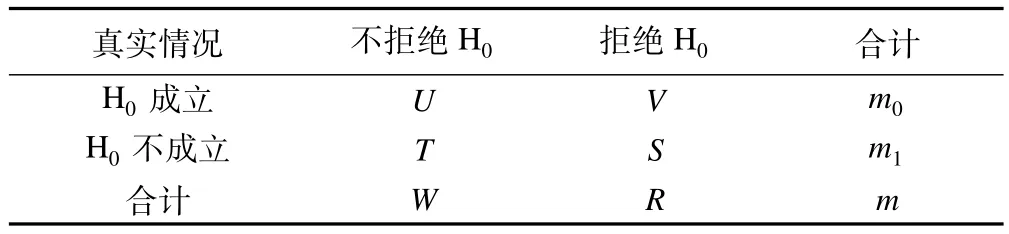
表1 多重檢驗的結果

1．控制FWER

FWER定義為至少犯一次Ⅰ類錯誤的概率，FWER＝P（V≥1），是傳統的多重檢驗中廣泛應用的控制Ⅰ類錯誤的指標。控制FWER的方法有經典的Bonferroni方法，當pi＜α／m時，拒絕相應的假設，公式1證明了Bonferroni方法可將FWER控制在π0α水平。

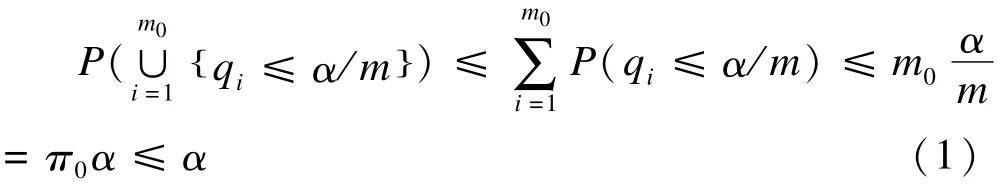
由此，當真實的H0全部成立時控制FWER是弱控制，此時FWER被控制在α水平；當真實的H0部分成立時控制FWER是強控制，且若不成立的H0的個數很多，FWER將被控制在遠低于α的水平，此時Bonferroni方法便會很保守［7］。因此Holm在1979年提出Holm方法［8］，在Bonferroni方法基礎上，迭代進行檢驗，第一步拒絕pi＜α／h0的假設，h0＝m；第二步排除掉第一步已經拒絕的假設，剩余沒有被拒絕的假設數為h1，拒絕pi＜α／h1的假設；以此類推，直到沒有假設被拒絕為止。Holm證明該方法能將FWER控制在α水平。Holm方法的另一種解法是首先將P值從小到大進行排序即p（1）≤p（2）≤…≤p（m），將p（i）與α／(m-i+1)進行比較，得到最小的j滿足p（j）＞α／(m-j+1)，然后拒絕所有j-1假設。Bonferroni和Holm方法都沒有對P值之間的關系做假設，即對P值的聯合分布沒有假設。Hochberg［9］利用成立的H0滿足弱PDS假設，在Holm方法基礎上進行了修改，Hochberg方法是首先將P值從小到大進行排序即p（1）≤p（2）≤…≤p（m），將p（i）與α／(m-i+1)進行比較，得到最大的j滿足p（j）＜α／(m-j+1)，然后依次拒絕所有j假設。Westfall＆Young［10］利用排列抽樣方法來控制FWER，其原理是在H0假設成立條件下，樣本來自相同的總體，可以對原始樣本進行重新抽樣，得到統計量的分布并進行檢驗。排列抽樣方法應用很廣，不僅可以用來控制FWER，也可以控制FDR等。Westfall＆Young的方法雖然在P值之間不獨立時效能比前面提到的方法高，但是排列抽樣對原假設間的一致性有要求。

隨著基因工程和下一代測序技術的迅猛發展，產生龐大的生物信息數據，通過在多重檢驗中控制FWER來控制Ⅰ類錯誤，對于探索性研究而言結果太過保守，FWER將每個假設檢驗的可信度控制在1-α水平，這只能識別出少數有意義的基因或者變量，且在嚴格控制Ⅰ類錯誤的同時其Ⅱ類錯誤偏大。它的優勢在于對每一個假設都嚴格控制Ⅰ類錯誤，在其選出的基因集中任意子集都對Ⅰ類錯誤有很好的控制，適用于對每個假設均有要求的驗證性研究。

2．控制FDR

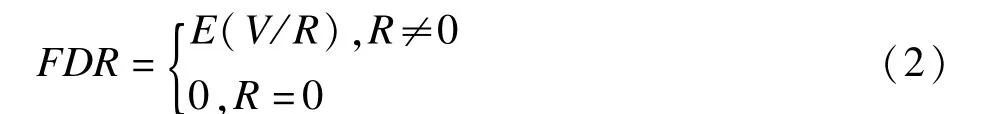
FDR與FWER之間的關系為：當m0＝m時，即全部原假設均成立，此時FDR的控制與FWER的控制等價；當m0＜m時，FDR小于或者等于FWER，因此，FDR相當于弱控制FWER［11-12］。

B-H方法可簡單表述為：先將P值從小到大進行排序即p（1）≤p（2）≤…≤p（m），然后將p（i）與iα／m進行比較，將FDR控制在α水平，定義j＝max {i：p（i）≤iα／m}，然后拒絕所有j假設，若沒有滿足條件的i存在，則沒有假設被拒絕。Benjamini＆Hochberg已證明當P值間相互獨立的時候，B-H方法能將FDR控制在π0α水平而不是α水平，故其結果有些保守。大量文獻在B-H的方法基礎上進行了改進，如將iα／m換為iα／（π＾0m），其中π＾0是π0的估計值，并針對π0的估計提出很多方法，該類方法為“自適應”方法［13-14］。原始的B-H方法要求P值間相互獨立，而當P值間不獨立時，許多研究者提出了相應的改進方法以及一些基于重抽樣的方法，如Yekutieli提出了ssBH方法［15］，Benjam ini＆Yekutieli提出基于排列抽樣的方法但是沒有完全證明該方法能控制FDR［16］，Joseph［17］等以及Troendle［18］提出了基于bootstrap的方法也能漸近控制FDR，但bootstrap的方法要求真實H0對應的P值的聯合分布的極限滿足可交換性［19］。除了控制FDR，還有一類方法是對選出的結果集的FDP（false discovery proportion）進行估計。FDR控制與FDP的估計是有區別的。例如：某個研究者重復一個實驗z次，采用控制FDR的方法進行分析，那么可能得到z個不同的結果集Ri，i＝1，…，z，每一個結果集都有其未知的FDP，記為Qi。當Z很大時，Qi的期望將接近FDR的控制水平。Q＾i為第i個結果集的FDP的估計值［7］。FDP的估計方法大多是從貝葉斯角度解釋，幾個代表性的方法是Storey 2003年提出的q-value法、Tusher 2001年提出的SAM（significance analysis ofm icroarray）方法、Efron 2001年提出的基于經驗貝葉斯的方法等，2012年劉晉等對這類方法進行了比較詳細的介紹［12］。在P值間不獨立的情況下，Fan等［20-21］在Storey［22］和Friguet［23］基礎上，提出PFA（principal factor approximation）法，該方法在進行多重檢驗校正時，通過因子分析將變量間相關關系考慮在內，提出適用于任意不獨立情況的FDP的近似公式和一致估計。除此之外，一些文獻對FDP的置信區間進行了估計［24-25］，如Meinshausen基于排列抽樣的方法。

目前在基因數據分析領域的多重比較問題中，FDR已經成為一個標準有效的反映Ⅰ類錯誤的指標，適用于探索性研究，在整體上控制Ⅰ類錯誤的同時能篩選出更多有意義的基因。然而FDR也存在一定的局限性，其一是FDR是隨機變量Q的期望值，當P值間不獨立時或者一些FDR估計方法的假設不滿足時，分析結果中Q＾的變異可能會增大［7，12］；其二是控制FDR的條件下得到的分析結果是從整體上控制了Ⅰ類錯誤，無法保證控制了每個假設或者每個結果的子集的Ⅰ類錯誤。因此研究者在解釋其結果時需要注意保持結果集的完整性［7］。

基于LASSO類方法的控制Ⅰ類錯誤的策略和技術

隨著生物信息技術的快速發展、大數據時代的到來，高維數據分析問題不斷涌現（本文中高維數據是指p＞n的情況，p和n分別表示自變量個數和樣本量），面對復雜數據建模時如何更加準確的篩選變量成為很重要的問題。隨著計算能力的提高和算法的不斷改進，懲罰類方法因其通過好的算法能執行較大維度的變量選擇過程、得到稀疏解而逐漸受到重視，是目前比較流行的變量選擇方法。該類方法假定模型具有稀疏性，即真實模型中很多自變量的回歸系數為0，其思想是在最小化損失函數或者最大化似然函數的同時增加一個懲罰項來篩選變量并估計其回歸系數，將回歸系數不為零的變量直接選入結果集中。常見的懲罰類方法有：LASSO、SCAD（smoothly clipped absolute deviation）、彈性網（elastic net）、MCP（minimax concave penalty）等。

1．LASSO中關于調整參數選擇的傳統方法

基于LASSO的變量選擇及回歸系數的估計，在很大程度上受調整參數λ的影響，因為調整參數值的大小影響著模型的復雜程度及模型的收斂速度，因此選擇合適的調整參數十分重要［26-27］。傳統的選擇調整參數的方法大致分為兩類：交叉驗證（cross validation，CV）和信息準則（information criteria）。

（1）交叉驗證

最常用的交叉驗證是K折交叉驗證（K-fold cross-validation），K為整數，1＜K≤n。該方法的過程是：首先將原始樣本Γ拆分成K個相同大小的子樣本，將其中一個子樣本選為驗證數據集Γv，其余K-1個子樣本為訓練數據集Γ-Γv，利用訓練數據集來建立模型，然后用擬合模型來預測驗證數據集，計算驗證集的預測值與真實值間的偏差，重復以上過程K次，計算平均偏差，選擇平均偏差最小時對應的調整參數值。

基于最小二乘的K折交叉驗證的目標函數為［28］：

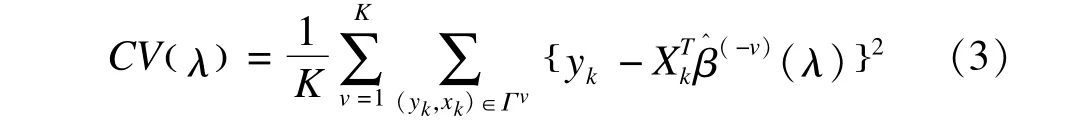
其中，β＾（-v）（λ）表示去掉（yk，xk）∈Γv后的回歸系數估計值，使CV（λ）取得最小值時對應的λ為最終模型的調整參數。

基于對數似然函數的K折交叉驗證的目標函數為［27］：

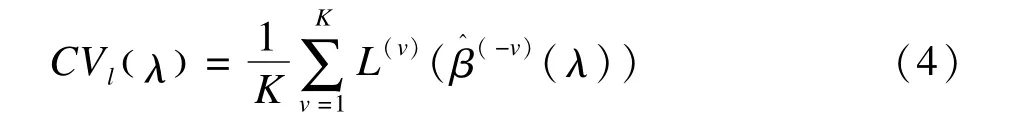
其中，β＾（-v）（λ）表示去掉第v份數據后的回歸系數估計值，L（v）（β＾（-v）（λ））表示第v份數據為驗證集時求得的對數似然函數值，使CVl（λ）取得最大值時對應的λ為最終模型的調整參數。

當K＝n時的交叉驗證稱為留一法（leave-oneout），該方法是對真實的預測誤差的漸近無偏估計，但是該法方差很大且計算量龐大［26］。Tibshirani1996年使用廣義交叉驗證（generalized cross validation，GCV）選擇調整參數，GCV在CV的基礎上將有效參數的個數考慮在內估計預測誤差。

（2）信息準則

信息準則一般包括模型擬合程度的測量（如似然函數或損失函數）以及對模型復雜程度的懲罰（懲罰乘子an）兩部分［29］。對于一個給定的統計模型如線性模型、生存模型，不同的信息準則方法的主要區別在于如何對模型的復雜程度進行懲罰，然而，對于選擇真實的模型而言，如何通過對模型復雜程度進行合理的懲罰來優化信息準則十分關鍵［30］。常用的信息準則有：AIC（Akaike information criterion）、BIC（Bayesian information criterion）、RIC（Risk inflation criterion）［31-33］等。an＝2和an＝log（n）分別對應的是AIC和BIC，an＝2log（p）為RIC，其中n為樣本量，p為非零回歸系數的個數。Yang和Wang指出CV以及GCV類似于傳統的AIC，三種方法在高維數據情形下均易出現過擬合，且AIC不是一致的信息準則［34-36］。Wang［36］的研究表明針對SCAD，BIC能一致的選擇真實的模型，但是隨著樣本量增大，BIC得到的結果可能會太保守，易遺漏一些重要的變量［37］。

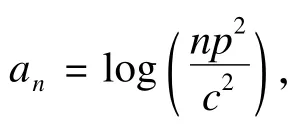
2．線性模型中基于LASSO類方法的控制Ⅰ類錯誤的方法

假設有n個樣本，y表示研究的反應變量，X為n ×p維的自變量矩陣，β是回歸系數，z是隨機誤差，z～N 0，σ2

()I。線性模型為：

基于LASSO的目標函數為：

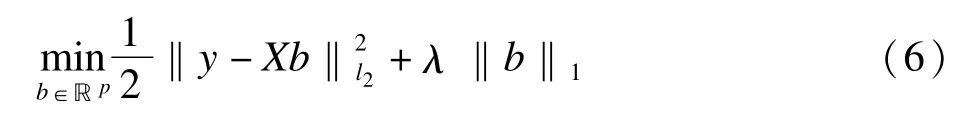
其中b是β的估計值，λ是調整參數。

（1）平穩選擇（stability selection）

平穩選擇法是將變量選擇算法和再抽樣技術相結合的方法，由Meinshausen和Bühlmann［42］提出，通過計算機對樣本進行隨機無放回抽樣得到樣本量為n／2的子樣本I，然后利用LASSO等懲罰回歸方法進行變量選擇，選入模型的變量估計為β＾λj()I，選入模型的變量集為：

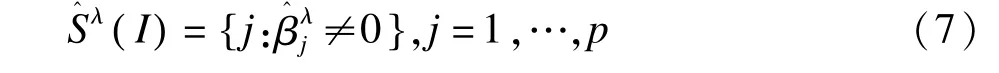
對不同的λ，每個變量j被選入模型的概率為：

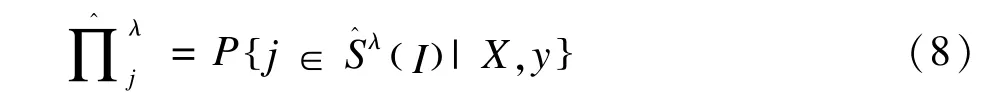
平穩選擇法將其中被選取概率大于閾值的變量選入最終模型，最終變量集為：

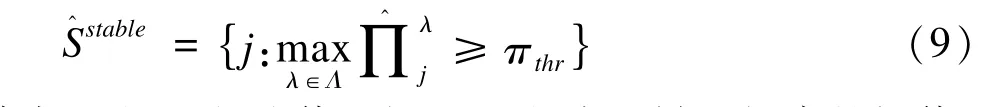
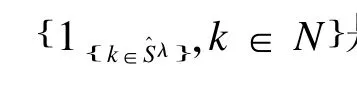
平穩選擇法在R軟件中可以實現。一般隨機抽取子樣本數達到500到1000即可，其計算成本較交叉驗證相差不多甚至更低［43-45］。該方法不單獨使用，而是與其他變量選擇方法結合使用，應用于不同模型中。該法通過再抽樣技術降低了模型結果對調整參數選擇的敏感性，并達到了控制Ⅰ類錯誤的目的。但是由于基因之間往往存在一定的關聯，其選擇變量集可交換的假設不一定成立，且有文獻報道在真實有意義的變量數極少的情況下，該方法的FDR值有時會很高，失去其控制Ⅰ類錯誤的作用［37］。

（2）SLOPE

SLOPE（sorted L-one penalized estimation）方法［3，46-48］，該法是在LASSO的基礎上結合控制FDR的B-H方法提出的。其模型是：

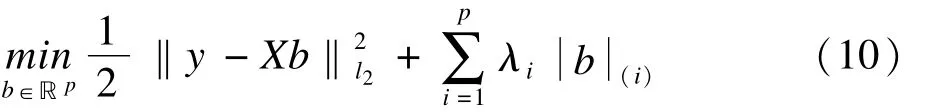
其中λi表示第i個變量的調整參數值，b（i）表示第i個變量的回歸系數絕對值，λi滿足λ1≥λ2≥…≥λp≥0降序排列，且λi的順序根據λBH（i）來決定，相應的

SLOPE方法首先在X是正交矩陣的條件下（XTX＝Ip），根據線性模型公式5構造y～，模型為：

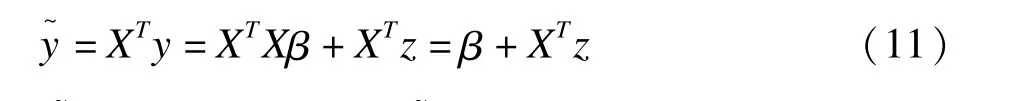
其中y～∈N(β，σ2Ip)，當時拒絕原假設。其次，在處理高維數據的LASSO方法基礎上進行改進，不同效應的變量對應的調整參數值不同，令λBH（i）＝z（1-i·α／2p），其中z(α)為標準正態分布的分位數，λi＝λBH（i）·σ，根據λi來選擇估計變量。Bogdan等證明在X滿足正交矩陣的條件下SLOPE方法能將FDR控制在α水平內。

當X不滿足正交矩陣的條件時，Bogdan等對λBH（i）進行了調整，在計算某一變量的λBH（i）時將其他變量的影響考慮在內，提出λG(i)：

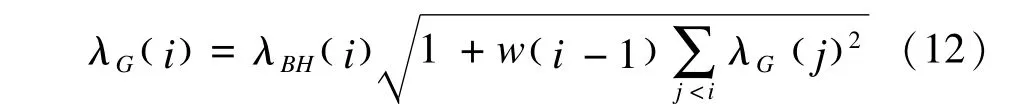
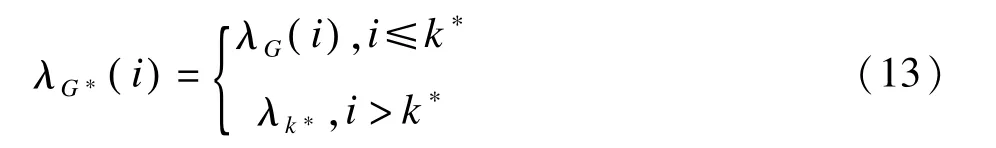
其中k*＝k( n，p，q)為最小的λG(i)的位置，λk*為λG(i)的最小值。

SLOPE借鑒多重檢驗校正中B-H方法的思想（B-H方法對P值從小到大排序，越小的p（i）其對應的檢驗水準iα／m值越小即檢驗水準越嚴格）改進LASSO，對不同效應的變量檢驗水準不同，效應越大的變量相應的檢驗水準越嚴格，其目的是為了控制FDR。SLOPE與LASSO的共同點在于兩者對β＾i的估計均為有偏估計，不同點在于LASSO法只選擇一個合理的λ值，根據估計β，Zi不為0，不同變量受到相同的懲罰。SLOPE根據λi來選擇估計變量，不同的變量受到的懲罰不同，值越大的變量λi越大。鑒于SLOPE是有偏估計的方法，Bogdan等在其文章中并不推薦利用SLOPE對進行直接估計，而是建議使用兩階段法，第一階段采用SLOPE法篩選出有意義的變量，第二階段對篩選出的變量利用普通最小二乘法估計其回歸系數。SLOPE方法在R、Matlab軟件中可以實現。

（3）Knockoffs filter

Barber和Candès［49］提出一種新的在有限樣本情況下篩選變量的方法，對任何自變量矩陣X∈Rn×p，n≥p，構造相應的knockoff變量矩陣X～，并將其與原始變量一同放入線性模型中，通過構建關于原始變量Xj與knockoff變量X～j的統計量Wj、確定統計量的界值T來控制線性模型中的FDR。

Knockoffs filter方法的過程分為三部分：

①對每一個原始變量Xj，j＝1，…，p構造knockoff變量X～j，要求knockoff保持原始變量之間的相關結構，即滿足XTX＝X～TX～＝∑，XTjX～k＝XTjXk，j≠k，且假設∑矩陣可逆，同時要求knockoff變量X～j與原始變量Xj間相似程度盡可能地低，即對于XTX～＝∑－diag()s盡量選擇大的s值。

②每對原始變量Xj和knockoff變量X～j構建一個統計量Wj。Barber和Candès在2014年的文章中給出很多種構建統計量Wj的方式，本文只詳述其中之一說明Wj的意義。在LASSO公式（6）基礎上，將自變量矩陣X換為增廣矩陣X X[]～，定義Zj為原始變量Xj首次進入模型時的λ值，Zj＝supλ：β＾j()λ≠{

}0，相應的Z～j為變量X～j首次進入模型時的λ值，對于每對原始變量Xj和knockoff變量X～j，構建統計量Wj：

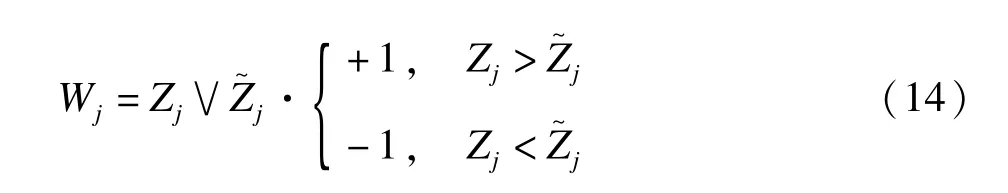
當Zj＝Z～j時，Wj＝0，若Wj為正并且值越大，說明原始變量Xj比knockoff變量X～j越早進入模型，則越有理由拒絕原假設。

③定義統計量的界值T，將滿足Wj≥T的自變量選入模型。設FDR控制水平為q，在原假設βj＝0成立情況下，原始變量Xj與knockoff變量X～j兩者誰先進入模型是隨機性的，即Wj的正負號是隨機的，那么對于任意的t，＃｛j：βj＝0 and Wj≥t｝＝d＃｛j：βj＝0 and Wj≤－t｝，其中＝d代表同分布。因此在t時，FDP的knockoff估計值為：

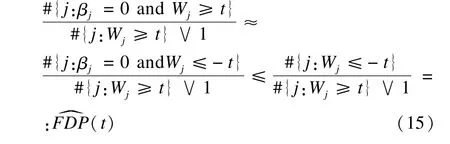
根據FDP的knockoff估計值定義T，T＝m in｛t∈W：FDP＾（t）≤q｝，最終界值T為：

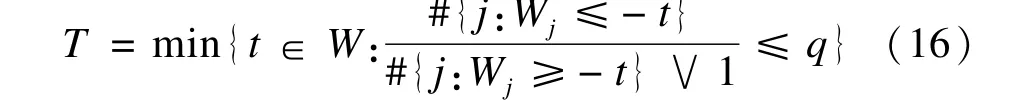
Knockoffs filter方法的關鍵之一在于knockoff變量的構造，當樣本量n≥p時，Barber和Candès描述了如何構造X～以及如何選擇合適的s值，但是當樣本量n＜p時，∑矩陣可逆的假設不再滿足，該方法不能直接使用，Barber和Candès［49］建議可以先使用一些降維的方法，再使用Knockoffs filter方法。Reid和Tibshirani［50］首先使用聚類處理自變量間相關的問題實現降維，然后用每個類別中選出的代表性的變量建模通過Knockoffs filter方法控制FDR。Barber和Candès［51］新提出一種分析策略應用于樣本量n＜p的情況，該策略將觀測分成兩組，第一組觀測的數據用于篩選潛在的有意義的自變量，其次在篩選出的變量基礎上用第二組觀測的數據，通過Knockoffs filter方法進行統計推斷。目前Knockoffs filter方法可以通過R軟件實現。

3．Cox模型中基于LASSO的控制FDR的方法

基于Cox模型的LASSO，其最大化目標函數為：

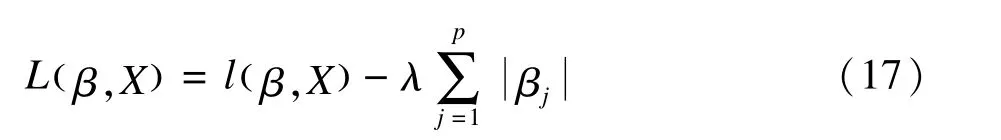
其中lβ，()X是Cox模型的對數似然函數，p為自變量個數。LASSO作為生存分析領域中常用的處理高維數據的方法之一，篩選的變量結果中存在FDR過高的問題，而調整參數的選擇很大程度上影響了LASSO的變量選擇和回歸系數的估計。Ternès，Rotolo和M ichiels［37］針對傳統的交叉驗證法容易出現過擬合的問題，提出了一種改進的調整參數的選擇方法，即pcvl（penalized cross-validated log-likelihood，pcvl），該方法主要在傳統交叉驗證的目標函數中加入懲罰項，以實現模型在滿足擬合優度與模型稀疏程度兩者之間的折中。

Ternès，Rotolo和M ichiels文章中傳統K折交叉驗證的目標函數是：

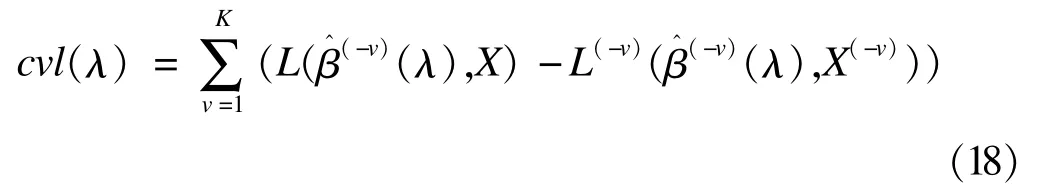
其中β＾（－v）（λ）表示去掉第v份數據后的回歸系數估計值，L（β＾（－v）（λ），X）表示全部數據求得的對數似然函數值，L（－v）（β＾（－v）（λ），X（－v））表示去掉第v份數據時求得的對數似然函數值，使cvl（λ）取得最大值時對應的λ為模型的調整參數，記為λ＾cvl。該函數參考Verweij和van Houwelingen［52］文章中對生存分析中交叉驗證法的介紹，與公式（4）的差別在于后者是利用全部數據的對數似然函數值與去掉第v份數據時求得的對數似然函數值之差來求第v份數據的對數似然函數，而且并沒有取平均值。

令λ0表示沒有變量進入模型時λ的最小值，即λ0＝minλ｜p{}＝0，懲罰項為：

Ternès，Rotolo和M ichiels將pcvl方法與傳統CV法、AIC、RIC、自適應LASSO和平穩選擇法進行了比較，模擬數據結果顯示pcvl方法的優勢在于控制FDR的情況下也能將假陰性率控制在較低水平。但是該方法是從適當增加λ值以減少LASSO篩選出的變量數的角度控制FDR，無法在建模時給定FDR的理想水平實現精確的FDR的控制。

表2 基于LASSO類方法的控制Ⅰ類錯誤方法的比較

展 望

本文首先回顧了多重假設檢驗中Ⅰ類錯誤控制方法，根據Ⅰ類錯誤控制指標的不同分為兩大類：控制FWER的方法和控制FDR的方法，然而基因間不獨立的問題對多重檢驗結果產生了一定的影響，同時在多變量情況下如何處理高維數據的問題也亟待解決，因此一些變量選擇方法如懲罰類方法成為如今研究的熱點。本文針對LASSO這一變量選擇方法存在的FDR過高的問題，介紹了四種方法，分別為平穩選擇法、SLOPE、Knockoffs filter和pcvl方法，已有一些研究分別將平穩選擇法、SLOPE和pcvl方法與傳統的調整參數選擇方法進行了比較且結果顯示平穩選擇法、SLOPE和pcvl方法可以有效控制Ⅰ類錯誤，但這些方法各有優劣及適用條件，并非在任何數據情況下都有效，因此在應用這些方法時需注意適用條件是否滿足。其中一些方法如平穩選擇、Knockoffs filter等也可以擴展到其他懲罰回歸模型中。LASSO懲罰估計是有偏的，不滿足oracle的三個性質，未來如何將這些控制Ⅰ類錯誤的方法應用于其他懲罰類方法如SCAD、MCP等還需要進一步研究。

［1］Benner A，Zucknick M，Hielscher T，et al．High-dimensional Cox models：the choice of penalty as part of themodel building process．Biometrical Journal，2010，52（1）：50-69．

［2］Shojaie A，M ichailidis G．Penalized likelihood methods for estimation of sparse high-dimensional directed acyclic graphs．Biometrika，2010，97（3）：519-538．

［3］Bogdan M，Berg EVD，Su W，et al．Statistical estimation and testing via the sorted L1 norm．arXiv：1310．1969，2013．

［4］王彤，易東．臨床試驗中多重性問題的統計學考慮．中國衛生統計，2012，29（3）：445-450．

［5］Block HW，Savits TH，Shaked M．A concept of negative dependence using stochastic ordering．Statistics＆Probability Letters，1985，3（2）：81-86．

［6］Sarkar SK，Guo W．On a generalized false discovery rate．Mathematics，2009，37（3）：1545-1565．

［7］Goeman JJ，Solari A．Multiple hypothesis testing in genomics．statistics in medicine，2014，33（11）：1946-1978．

［8］Holm S．A simple sequentially rejectivemultiple test procedure Scandinavian Journal of Statistics，1979，6（2）：65-70．

［9］Hochberg Y．A sharper Bonferroniprocedure formultiple tests of significance．Biometrika，1988，75（4）：800-802．

［10］Westfall PH，Young SS．Resampling-Based Multiple Testing：Examples and Methods for P-Value Adjustment．NewYork：W iley-Interscience，1993．

［11］Benjam ini Y，Hochberg Y．Controlling the False Discovery Rate：APractical and Powerful Approach to Multiple Testing．Journal of the Royal Statistical Society，1995，57（1）：289-300．

［12］劉晉，張濤，李康．多重假設檢驗中FDR的控制與估計方法．中國衛生統計，2012，29（2）：305-308．

［13］Benjam ini Y，Hochberg Y．On the Adaptive Control of the False Discovery Rate in Multiple Testing w ith Independent Statistics．Journal of Educational And Behavioral Statistics，2000，25（1）：60-83．

［14］Benjam ini Y，Krieger AM，Yekutieli D．Adaptive linear step-up procedures that control the false discovery rate．Biometrika，2006，93（3）：491-507．

［15］Yekutieli D．False discovery rate control for non-positively regression dependent test statistics．Journalof Statistical Planning and Inference，2007，138（2）：405-415．

［16］YekutieliD，Benjam ini Y．Resampling-based false discovery rate controlling multiple test procedures for correlated test statistics．Journal of Statistical Planning and Inference，1999，82（1-2）：171-196．

［17］Romano JP，Shaikh AM，Wolf M．Control of the false discovery rate under dependence using the bootstrap and subsampling．Test，2008，17（3）：417-442．

［18］Troendle JF．Stepw ise normal theory multiple test procedures controlling the false discovery rate．Journal of Statistical Planning and Inference，2000，84（1-2）：139-158．

［19］劉莉．兩兩多重比較的FDR控制．上海：上海交通大學，2015．

［20］Xu H，Gu W，Fan J．Control of the False Discovery Rate Under Arbitrary Covariance Dependence．arXiv：1012．4397，2010．

［21］Fan J，Han X，Gu W．Estimating False Discovery Proportion Under Arbitrary Covariance Dependence．Journal of the American Statistical Association，2012，107（499）：1019-1035．

［22］Leek JT，Storey JD．A general framework formultiple testing dependence．Proceedings of the National Academy of Sciencesof the United States of America，2008，105（48）：18718-18723．

［23］Friguet C，Kloareg M，Causeur D．A Factor Model Approach to Multiple Testing Under Dependence．Journal of the American Statistical Association，2009，104（488）：1406-1415．

［24］Goeman JJ，Solari A．Multiple testing for exploratory research．Statistical Science，2011，26（4）：584-597．

［25］Meinshausen N．False discovery control formultiple tests of association under general dependence．Scandinavian Journal of Statistics，2006，33（2）：227-237．

［26］Hastie T，TibshiraniR，Friedman J．The Elementsof Statistical Learning-Data M ining，Inference and Prediction，2nd edn．New York：Springer，2009，241-245．

［27］王慧．生存分析中半參數模型的變量選擇方法及其模擬研究．太原：山西醫科大學，2013．

［28］Arlot S，Celisse A．A survey of cross-validation procedures formodel selection．Statistics Surveys，2010，4（0）：40-79．

［29］Nishii R．Asymptotic Properties of Criteria for Selection of Variables in Multiple Regression．Annals of Statistics，1984，12（2）：758-765．

［30］Fan Y，Tang CY．Tuning parameter selection in high dimensional penalized likelihood．Journal of the Royal Statistical Society，2013，75（3）：531-552．

［31］Akaike H．A New Look at the Statistical Model Identification．Automatic Control IEEE Transactions on，1974，19（6）：716-723．

［32］Schwarz G．Estimating the Dimension of a Model．Annals of Statistics，1978，6（2）：15-18．

［33］Foster DP，George EI．The Risk Inflation Criterion for Multiple Regression．Annals of Statistics，1994，22（4）：1947-1975．

［34］Shao J．An asymptotic theory for linear model selection．Statistica Sinica，1997，7（2）：221-242．

［35］Yang Y．Can the strengths of AIC and BIC be shared？A conflictbetween model indentification and regression estimation．Biometrika，2005，92（4）：937-950．

［36］Wang H，LiR，TsaiCL．Tuning Parameter Selectors for the Smoothly Clipped Absolute Deviation Method．Biometrika，2007，94（3）：553-568．

［37］Ternes N，Rotolo F，M ichiels S．Empirical extensions of the lasso penalty to reduce the false discovery rate in high-dimensional Cox regression models．statistics in medicine，2016，35（15）：2561-2573．

［38］Bogdan M，Ghosh JK，Doerge RW．Modifying the Schwarz Bayesian information criterion to locate multiple interacting quantitative trait loci．Genetics，2004，167（2）：989-999．

［39］Bogdan g，M．？S，Ghosh JK．Selecting explanatory variables w ith themodified version of the Bayesian information criterion．Quality＆Reliability Engineering International，2008，24（6）：627-641．

［40］Chen J，Chen Z．Extended Bayesian information criteria formodel selection w ith largemodel spaces．Biometrika，2008，95（95）：759-771．

［41］Wang T，Zhu L．Consistent tuning parameter selection in high dimensional sparse linear regression．Journal of Multivariate Analysis，2011，102（7）：1141-1151．

［42］Meinshausen N，Bühlmann P．Stability selection．Journal of the Royal Statistical Society，2010，72（4）：417-473．

［43］勾建偉．懲罰回歸方法的研究及其在后全基因關聯研究中的應用．南京醫科大學，2014．

［44］Bühlmann P，Kalisch M，Meier L．High-Dimensional Statisticswith a View Toward Applications in Biology．Annual Review of Statistics＆Its Application，2014，1（1）：255-278．

［45］趙俊琴．基于Lasso的高維數據線性回歸模型統計推斷方法比較．太原：山西醫科大學，2015．

［46］Bogdan M，Berg Evd，Su W，et al．Statistical Estimation and Testing via the Ordered L1 Norm．arXiv：1310．1969，2013．

［47］Bogdan M，van den Berg E，SabattiC，et al．Slope-Adaptive Variable Selection Via Convex Optimization．Ann Appl Stat，2015，9（3）：1103-1140．

［48］Su W，Candes E．SLOPE is Adaptive to Unknown Sparsity and Asymptotically M inimax．Ann Appl Stat，2015，44（3）：1038-1068．

［49］Barber RF，Candès EJ．Controlling the false discovery rate via knockoffs．Annals of Statistics，2014，43（5）：2055-2085．

［50］Reid S，Tibshirani R．Sparse regression and marginal testing using cluster prototypes．Biostatistics，2016，17（2）：364-376．

［51］Barber RF，Candes EJ．A knockoff filter for high-dimensional selective inference．arXiv：1602．03574，2016．

［52］Verweij PJ，Van Houwelingen HC．Cross-validation in survival analysis．statistics inmedicine，1993，12（24）：2305-2314．

（責任編輯：郭海強）

國家自然科學基金項目（81473073）

△通信作者：王彤，E-mail：tongwang＠sxmu．edu．cn