不同刪失比例下AFT模型與Cox模型表現比較的模擬研究*

昆明醫科大學公共衛生學院流行病與衛生統計學系（650500） 肖媛媛 陳 瑩 何利平 喻 箴 許傳志

不同刪失比例下AFT模型與Cox模型表現比較的模擬研究*

昆明醫科大學公共衛生學院流行病與衛生統計學系（650500） 肖媛媛 陳 瑩 何利平 喻 箴 許傳志△

目的 評價當生存數據出現不同刪失比例的條件下，AFT模型和Cox模型的表現優劣。方法 采用自編SAS宏程序模擬不同參數設置、不同比例均勻刪失的Weibull分布，分別采用AFT模型和Cox模型對模擬產生的數據進行擬合，并從偏倚、準確性和覆蓋程度三個指標對兩個模型的表現進行評價。結果 在分布參數和自變量效應值固定的情況下，AFT模型在參數估計偏倚和準確性兩方面的表現卻始終優于Cox模型。刪失比例越大，AFT模型的表現相對而言越優異。而在覆蓋程度方面，對于相同參數設置及刪失比例的模擬數據，兩個模型的表現相似。結論 AFT模型的總體表現優于Cox模型，當刪失生存數據同時滿足兩類模型的應用條件時，應該優先選擇偏倚更小、準確性更高的AFT模型進行分析。

AFT模型 Cox模型 刪失比例 表現 模擬研究

作為最為常見的兩類生存分析模型，Cox模型與AFT模型在不同條件下的表現比較是一個引人關注的問題，也有部分學者曾經探討過，但大都集中在參數估計的準確度及數據擬合優度的比較方面。如Orbe等采用隨機數據模擬的方法比較了一類半參數AFT模型和Cox模型的擬合優度，發現半參數AFT模型得到的結果更為準確［1］；Qi在運用AFT模型和Cox模型擬合同一真實數據后發現AFT模型的擬合優度要高于Cox模型［2］；Sayehmir等［3］，Ponnuraja等［4］，Nawumbeni等［5］將AFT模型和Cox模型同時運用于真實數據，發現AFT模型的預測表現明顯優于Cox模型等。但目前尚無研究討論在應用條件同時滿足時，不同刪失數據比例下AFT模型和Cox模型的表現比較。本研究擬采用隨機數據模擬的方法對這一問題進行初步探討。

對象與方法

1．選擇模擬分布

要對AFT模型和Cox模型的表現進行對比，就必須采用同一模擬數據集。因此，模擬的數據集必須同時滿足AFT模型和Cox模型的應用條件，即比例風險和恒定加速失效因子。常見的生存分布類型中，只有兩種分布同時滿足上述兩個應用條件，指數分布（exponential distribution）和Weibull分布（Weibull distribution）。考慮到指數分布是Weibull分布的特例，為不失一般性，本研究選擇Weibull分布為模擬分布。

2．模擬設計

（1）模擬條件設定

為了集中討論不同參數條件下刪失比例對兩類模型表現的影響，在數據模擬前，我們對模擬數據的其他特征簡化設定如下：只研究單一自變量，且為了兼顧統計效能，該自變量取值定義為滿足參數為B（1，0．5）的二項分布；所有模擬組別均為大樣本（N＝1000），不考慮樣本含量對結果的影響；只考慮隨機刪失，且刪失分布定義為均勻分布；考慮到Weibull分布中尺度參數λ的作用僅為拉伸或壓縮原始分布，并不改變其形狀，因此總可以用固定系數將其還原為原始分布，故模擬研究中不再考慮它的變化對結果的影響，所有模擬組均設置為1。

（2）產生生存時間

目前在隨機模擬產生滿足比例風險假定的生存時間分布，即指數分布、Weibull分布和Gompertz分布時，經常采用的是Bender等于2005年提出的模擬方法［6］。本次研究也采用上述方法隨機產生生存數據，具體步驟為：①采用SAS統計分析軟件產成［0，1］上均勻分布的隨機變量U，樣本含量為N；②根據預先設定的分布參數λ、γ以及協變量的回歸系數向量β，結合生成的隨機變量U的取值，利用公式1轉換得到生存時間T，樣本含量同樣為N。

（3）生成含特定比例刪失的生存數據

在進行生存數據的隨機模擬研究時，刪失數據的生成遠比完整數據復雜得多，尤其是含特定比例刪失的數據。除非特別說明，本文所指代的刪失均為隨機刪失。在前期對相關領域文獻進行細致檢索和梳理后，我們發現：雖然有學者已經提出了一些含特定比例刪失生存數據的模擬方法，但這些方法或是在邏輯架構上就存在欠妥之處，或是經實際驗證無法得到設定刪失比例的生存數據。正是由于現有研究存在上述不足，在當前研究中，我們采用自行編制的SAS宏程序隨機模擬產生含特定比例刪失的生存數據。該宏程序的編制思路、步驟及具體的程序步驟我們已在前期發表的一項研究中進行過詳細描述［7］。

（4）模擬策略

前面已經述及，根據研究目的，模擬所需的部分非重點關注參數和特征已經設置為恒定。在設置模擬策略時，只重點關注Weibull分布形狀參數γ，比例風險效應系數β和刪失比例設定值P的變化對兩類生存分析模型表現的影響。因此，最終確定執行如下4組模擬，其中，每組模擬均執行刪失比例分別為10%、20%、30%、40%、50%、60%、70%、80%、90%的9小組模擬（表1）。

在進行模擬研究時，依據所要達到的估計值準確度的大小，可以采用公式（2）計算單次模擬的模擬次數［8］：

上式中，σ是所估計參數的標準差，δ是預先設定的參數估計精度，可用標準差的百分位數表示，Z1-（a／2）是標準正態分布下第1-（a／2）百分位數的取值，1-θ為檢驗效能。

本次研究中，δ取σ的15%，檢驗效能定為90%，由此計算得到的模擬次數為467次。為方便起見，每小組模擬重復次數統一取500次。

3．模型表現評價指標

隨機數據模擬研究在評價特定模型擬合變現時，通常采用如下三個方面的指標：偏倚（bias）、準確性（accuracy）和覆蓋程度（coverage）［8］。本次研究中將每次通過完整數據得到的參數估計值作為金標準，也從上述三個方面出發設定如下評價指標：

（1）偏倚：評價指標為采用刪失數據得到的模型參數估計值＾β與使用完整數據擬合模型得到的參數估計值＾β0相比的相對絕對偏差，其計算公式參見公式（3）：

（2）準確性：評價指標為采用刪失數據得到的模型參數估計值＾β的標準差＾S與使用完整數據擬合模型得到的參數估計值＾β0的標準差＾S0的比值，其計算公式參見公式（4）：

（3）覆蓋程度：覆蓋程度是指用模擬數據得到的效應估計值多大程度覆蓋了真實效應值。本次模擬研究采用顯著性一致率來評價覆蓋程度，定義為使用完整數據得到的參數估計值＾β0顯著（P＜0．05）的模擬次數（N）中，采用刪失數據得到的參數估計值＾β也同樣顯著的次數（Nacco）所占的百分比。其計算公式參見公式（5）：

結 果

1．偏倚

（1）兩模型總體比較

從圖1可以看出，在四組模擬策略下，不論生存分布的形狀參數γ及自變量X的效應系數β如何設置，隨著刪失比例的增加，Cox模型和AFT模型的偏倚都逐漸加大，但在任何刪失比例下，AFT模型的偏倚均小于Cox模型的偏倚。

在四組模擬策略下，隨著刪失比例的增加，AFT模型和Cox模型的偏倚之差逐漸增大。刪失比例在70%以下時，兩模型偏倚之差增速較緩；當刪失比例超過70%時，偏倚之差陡增。此外，在刪失比例小于70%時，模擬數據參數設置對兩類模型偏倚之差的影響不大，而當刪失比例大于70%時，隨著形狀參數γ的增大，或效應系數β的減小，AFT模型和Cox模型的偏倚之差迅速增大（圖2）。

（2）不同形狀參數下兩類模型的偏倚變化

從圖3可以看出：對兩類模型而言，當刪失數據比例小于60%時，形狀參數γ的變化對偏倚的影響不大；而當刪失比例大于60%時，隨著刪失比例的增加，γ對偏倚的影響逐漸增大。尤其是Cox模型，大約在缺失比例50%時，γ對偏倚的影響開始顯現，到缺失比例90%時，γ＝2時的偏倚比γ＝0．5時的偏倚大約9%（35．2%和26．2%）。對AFT模型而言，偏倚的增幅不明顯，同樣在缺失比例90%時，γ＝0．5和γ＝2的偏倚差距僅為不到2%（13．0%和11．2%）。

（3）自變量不同效應參數下兩類模型的偏倚變化

從圖4可以看出：在任一刪失比例下，當研究因素X的效應逐漸減弱時，Cox模型和AFT模型的偏倚均逐漸增大。偏倚的增加速度也隨刪失比例的增大而增大，尤其當刪失比例大于70%時，效應參數越小的組別偏倚的增大越快。如刪失比例從70%上升至90%、γ＝2、β＝0．2時，Cox模型偏倚的增加達到了1．1倍（43．3%到91．9%），雖然AFT模型在偏倚絕對值方面的表現明顯優于Cox模型，但其偏倚增速卻與Cox模型接近，為0．9倍（34．2%到65．7%）。

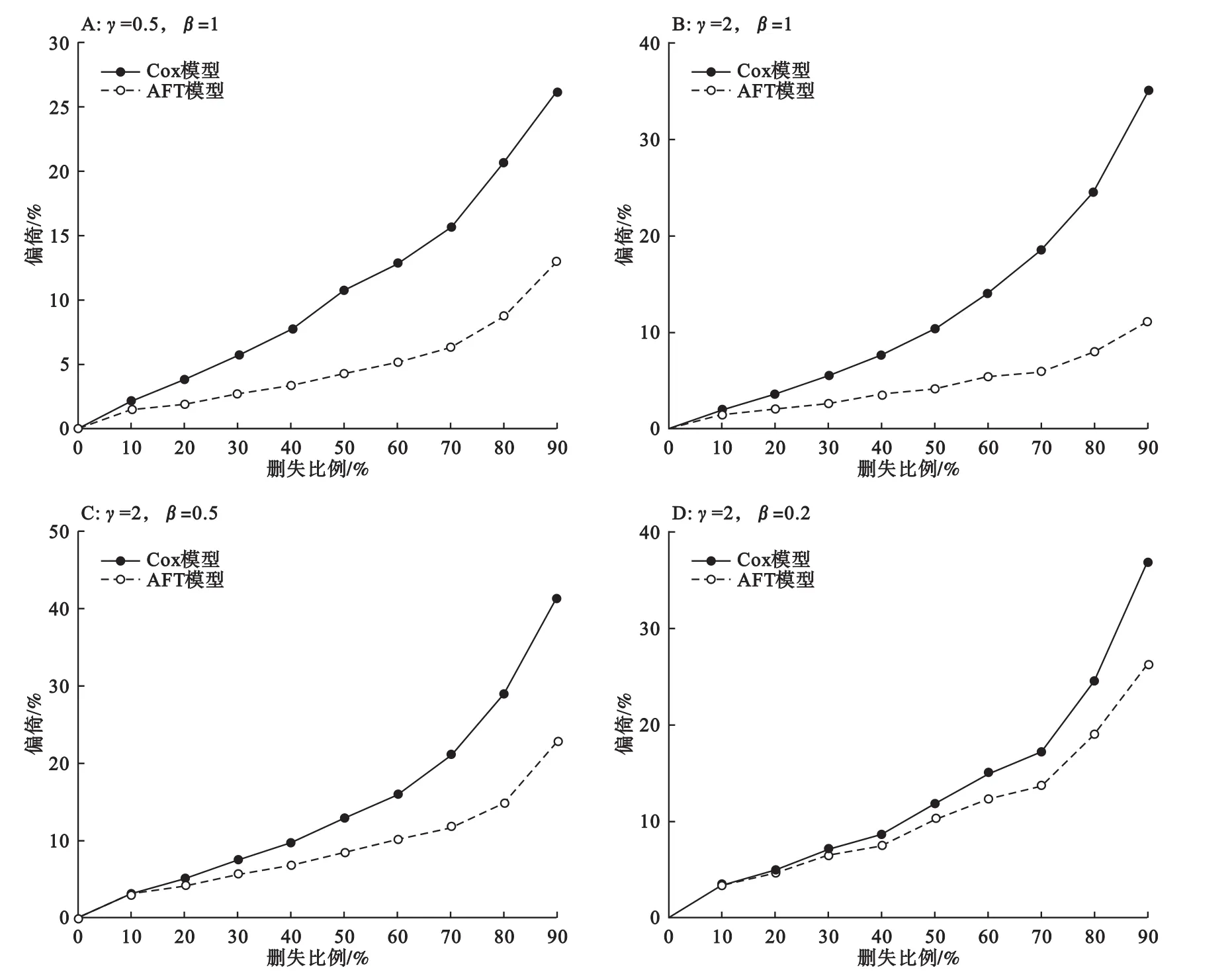
圖1 不同參數及刪失比例下Cox模型和AFT模型偏倚

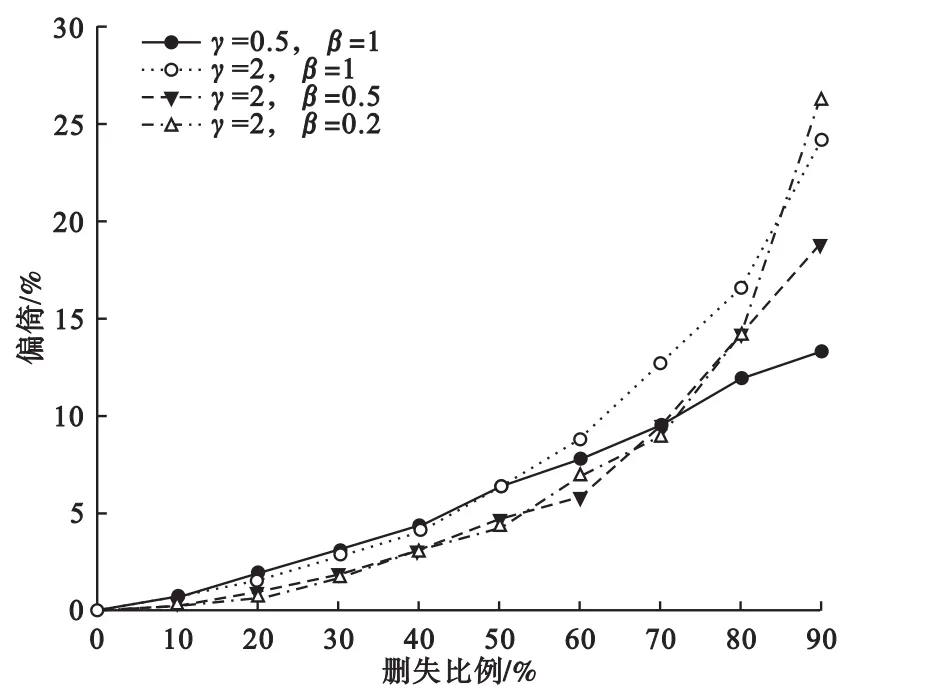
圖2 不同參數及刪失比例下Cox模型和AFT模型偏倚之差

2．準確性

對于Cox模型和AFT模型，隨著刪失比例的增加，其參數估計的標準差與通過完整數據得到的標準差之間的比值逐漸增大，意即其參數估計的準確性逐漸降低。尤其是在刪失比例大于70%后，準確性加速降低。生存時間形狀參數γ和自變量X效應系數β的變化對兩類模型參數估計的準確性無明顯影響：以四組模擬中刪失比例30%為例，Cox模型得到的準確性估計值皆為1．2，AFT模型得到的準確性估計值皆為1．14；再如刪失比例70%時，Cox模型得到的準確性估計值依次為1．85、1．84、1．83、1．83，AFT得到的準確性估計值依次為1．63、1．56、1．57、1．56。

在四組模擬數據中，在任一刪失比例下，AFT模型參數估計的準確性表現始終優于Cox模型，且差距隨刪失比例的增大而增大。當四組模擬數據刪失比例達到90%時，采用Cox模型計算得到的參數標準差是完整數據參數標準差的約3．2倍，而AFT模型介于2．4～2．7倍（圖5）。

3．覆蓋程度

不同刪失比例下Cox模型和AFT模型得到的顯著性一致率如表2所示。不難看出，在自變量X的效應較強時（β＝1），刪失比例的變化對兩種模型的顯著性一致率無影響，均為100%。而當自變量的效應逐漸減弱時，隨著刪失比例的增加，兩種模型在顯著性一致率方面的表現逐漸下滑，且下滑速度相當。如當β＝0．2，γ＝2時（組號＝4），對應Cox模型中X所導致的風險比為1．2，AFT模型中X加速失效因子為0．9，刪失數據比例為50%及以下時，兩種模型的顯著性一致率均大致高于80%。當刪失比例高于50%時，顯著性一致率加速下滑，特別當刪失比例達到90%時，兩種模型的顯著性一致率均僅為30%左右。

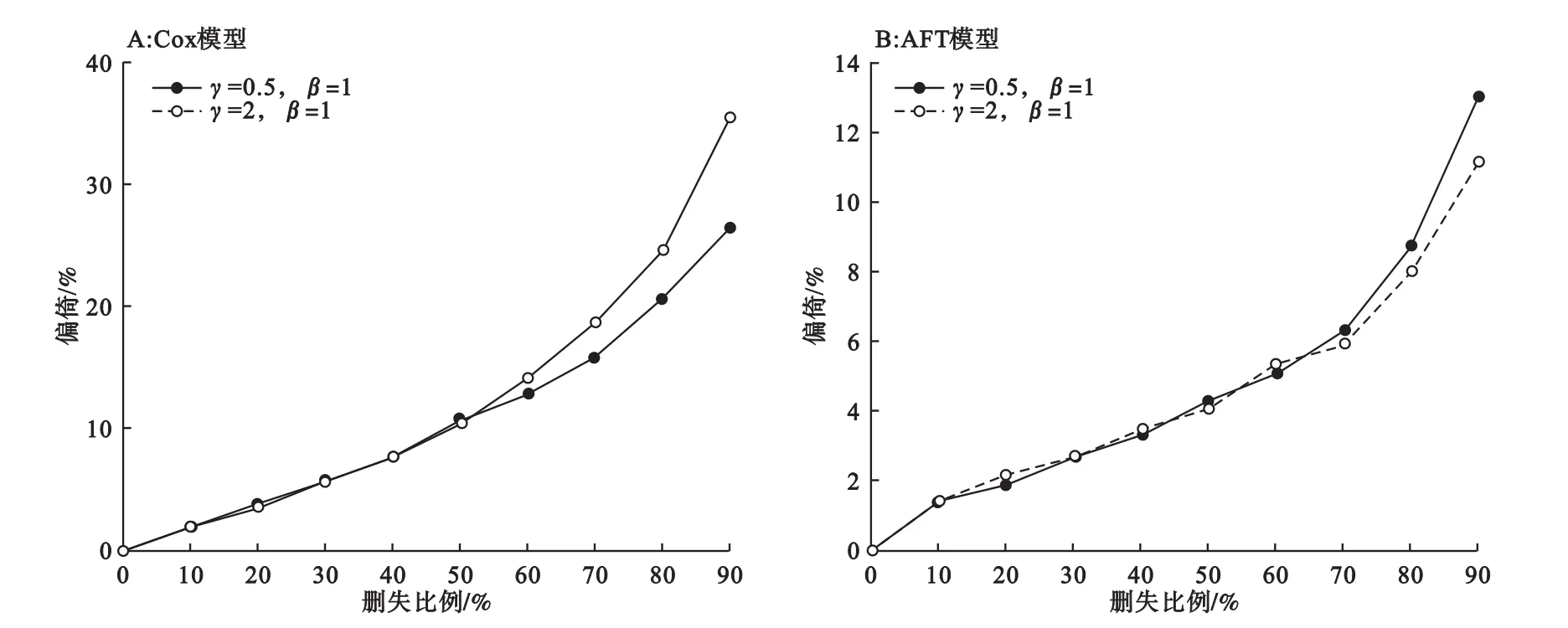
圖3 形狀參數γ不同時Cox模型和AFT模型偏倚隨刪失比例變化趨勢

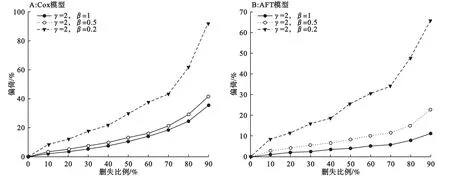
圖4 自變量X效應系數β不同時Cox模型和AFT模型偏倚隨刪失比例變化趨勢

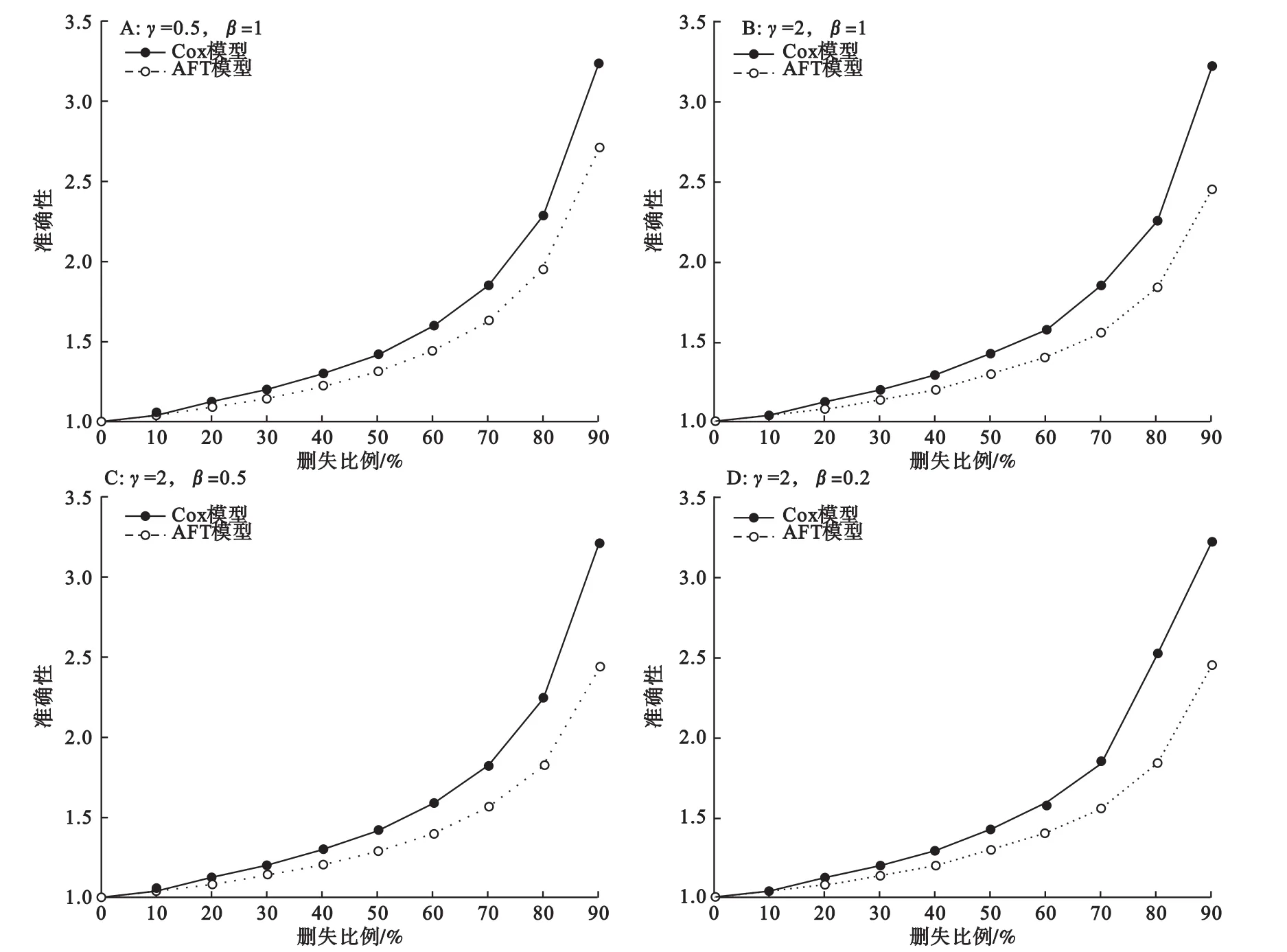
圖5 不同參數及刪失比例下Cox模型和AFT模型準確性

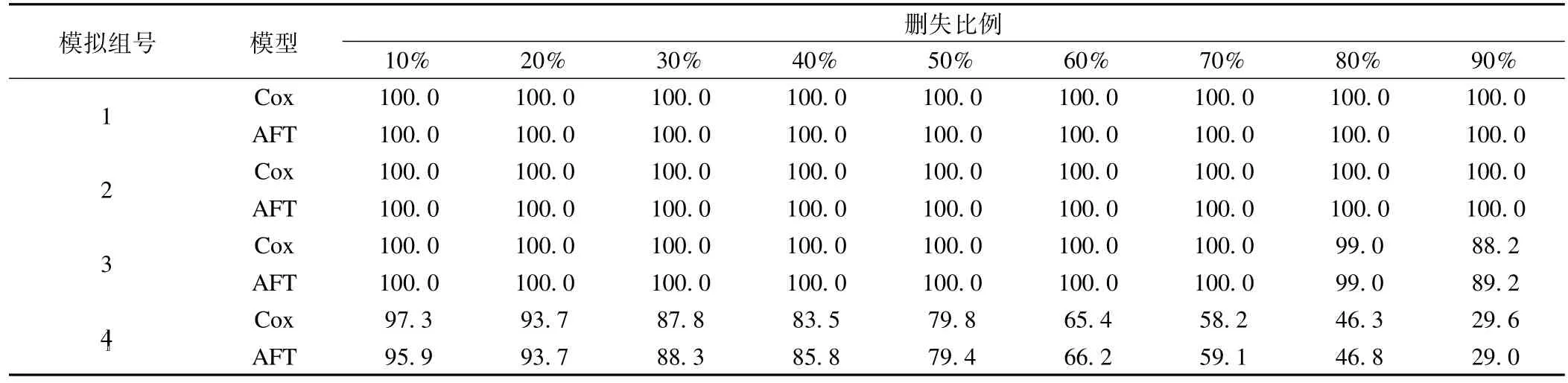
表2 不同參數及刪失比例下Cox模型和AFT模型顯著性一致率（%）

討 論

本研究以Weibull分布為模擬分布，討論了在分布參數和自變量效應值取值不同的情況下，生存時間刪失比例對Cox模型和AFT模型表現的影響。研究發現：在分布參數和自變量效應值固定的情況下，隨著生存時間刪失比例的增加，Cox模型和AFT模型在參數估計方面的偏倚均增大，準確性均降低，尤其是在刪失比例大于70%時，兩類模型在偏倚和準確性方面的表現更是加速下滑。其中，刪失比例對Cox模型表現的影響與前文提到的一項研究結果一致［8］，而生存數據刪失比例對AFT模型表現的影響則尚未查見既往文獻報道。

盡管隨著刪失比例的增加，兩類模型在偏倚和準確性方面的變化趨勢一致。但對于特定刪失比例的生存數據，在分布參數和自變量效應值固定的情況下，AFT模型在參數估計偏倚和準確性兩方面的表現卻始終優于Cox模型。刪失比例越大，AFT模型的表現相對而言越優異。以偏倚方面的表現為例，當生存分布的形狀參數γ＝2，自變量X的效應參數β＝1時，刪失比例為40%時，Cox模型的偏倚約為AFT模型的2倍，而當刪失比例增加至90%時，Cox模型的偏倚約為AFT模型的3倍。再從準確性方面來看，同樣的形狀參數和自變量效應參數情況下，刪失比例為40%時，Cox模型的參數標準差為金標準的1．3倍，AFT模型的參數標準差為金標準的1．2倍，當刪失比例增加至90%時，Cox模型的參數標準差增至金標準的3．2倍，而AFT模型的參數標準差卻只增至金標準的2．5倍。

在醫學研究中，生存分析一般都運用于縱向研究所獲取的數據。受限于研究的成本投入及倫理學標準，縱向研究的時間往往比較有限。正是因為如此，醫學領域所涉及的生存分析一般會包含較大比例的刪失數據。在Web of Science中隨機搜尋新近發表的腫瘤生存分析文獻就不難發現這一現象。如Heemskerk-Gerritsen等發表的一項關于乳腺癌的生存分析研究有88%的刪失［9］，再如Cardwell等發表的另一項關于乳腺癌生存分析的研究中，刪失數據占92%［10］。考慮到醫學研究中生存數據的特點和本次模擬研究所得到的結果，當生存數據同時滿足Cox模型和AFT模型的應用條件時，應該優先選擇偏倚更小、準確性更高的AFT模型進行參數估計。

當研究因素真實效應較弱時，如果生存時間刪失比例同時過高，則不論AFT模型還是Cox模型，其正確判斷真實效應顯著性的能力均受到較大影響。本次模擬中，研究因素HR＝1．2，即加速失效因子＝0．9時，若刪失比例為80%以上，則正確判斷的比例低于50%。因此在運用AFT模型或Cox模型進行生存分析時，一旦預判某一研究因素的真實效應較弱，同時生存時間刪失比例較大時，對分析結果的解讀需謹慎。

［1］Orbe J，Ferreira E，Nú?ez-Antón V．Comparing proportional hazards and accelerated failure timemodels for survival analysis．Statistics in Medicine，2002，21（22）：3493-3510．

［2］Qi J．Comparison of proportional hazards and accelerated failure time models［D］．University of Saskatchewan，2009．

［3］Sayehm iri K，Eshraghian MR，Mohammad K，et al．Prognostic factors of survival time after hematopoietic stem cell transplant in acute lymphoblastic leukem ia patients in Shariati hospital，Tehran．Journal of Experimental＆Clinical Cancer Research，2008，27：74．

［4］Ponnuraja C，Venkatesan P．Survivalmodels for exploring tuberculosis clinical trial data-an empirical comparison．Indian Journal of Science and Technology，2010，3（7）：755-758．

［5］Nawumbeni DN，Luguterah A，Adampah T．Performance of Cox proportional hazard and accelerated failure timemodels in the analysis of HIV／TB co-infection survival data．Research on Humanities and Social Sciences，2014，4（21）：94-102．

［6］Bender R，Augustin T，Blettner M．Generating survival times to simulate Cox proportional hazardsmodels．Statistics in Medicine，2005，24（11）：1713-1723．

［7］肖媛媛，許傳志，趙耐青．含特定比例均勻隨機刪失生存數據的SAS模擬實現．中國衛生統計，2016，33（6）：1058-1059．

［8］錢俊．生存分析中刪失數據比例對Cox回歸模型影響的研究．南方醫科大學，2009．

［9］Heemskerk-Gerritsen BA，Rookus MA，Aalfs CM，et al．Improved overall survival after contralateral risk-reducingmastectomy in brca1／2 mutation carriersw ith a history of unilateral breast cancer：a prospective analysis．International Journal of Cancer，2015，136（3）：668-677．

［10］Cardwell CR，Hicks BM，Hughes C，et al．Statin use after diagnosis of breast cancer and survival：a population-based cohort study．Epidemiology，2015，26（1）：68-78．

（責任編輯：鄧 妍）

國家自然科學基金（81460519）；云南省自然科學基金（2013FZ064）

△通信作者：許傳志，E-mail：xuchzhi＠qq．com