基于Kernel_PCA算法的中醫藥項目執行情況綜合評估*

湖北中醫藥大學信息工程學院（430065） 黃 瑤 肖 勇

基于Kernel_PCA算法的中醫藥項目執行情況綜合評估*

湖北中醫藥大學信息工程學院（430065） 黃 瑤 肖 勇△

近年來，中央財政用于支持全國中醫藥事業發展的專項資金屢創歷史新高，財政部等部門對中醫藥項目預算執行管理提出更高的要求［1-2］。中醫藥項目數據并不存在直接的線性關系，應用單一指標使用的評估方法很難直接和全面反映全國中醫藥項目總體執行情況。Kernel_PCA算法不是一種新型算法，它是由主成分分析法（principal component analysis，PCA）進一步發展而來，可處理非線性數據，通過非線性映射將初始數據空間投射到高維特征空間，然后在特征空間里進行主成分分析，把非線性問題轉化為線性問題。本文基于Kernel_PCA算法，綜合考慮全國各省份中醫藥項目的預算執行情況，運用多重填補法（multiple imputation，M I）對中醫藥項目數據進行預處理，采用多目標綜合優化思想，凝煉得到綜合評估，并將最終結果與現實情況對比驗證［3］。

M I與Kernel_PCA概述

本文研究的中醫藥項目執行數據存在某些項目無預算而導致數據缺失，因此對中醫藥項目執行數據降維處理前需要進行預處理。本文采用M I法，其定義如下［4-6］：M I法是通過某種方法對每一個缺失值都構造m個插補值（m≥2）產生m個完整數據集，這些值也反映了缺失值的不確定性，然后用分析完整數據集的統計學方法進行研究，在得到目標變量的估計前對這些結果進行綜合考量，使得出的結論更合理、可靠［7-9］。目前，M I法主要應用在社會科學、行為學和生物醫學等領域［10］。PCA是最小均方誤差意義上基于數據間的線性關系提取數據主要特征分量，是常用的高維數據降維算法之一，但PCA不能處理具有非線性性質的數據［11-14］。Kernel_PCA（Kernel Principal Component Analysis），也稱核主成分分析，由Scholkopf等人提出，是一種非線性主成分提取方法，基本思想是構造一個滿足Mercer條件的核函數，通過非線性映射將初始輸入空間R的數據集投影到高維特征空間F，然后在高維空間對映射數據做PCA處理，這個新空間可以增加數據的線性可分性，具有很強的非線性處理能力［15-16］。Kernel_PCA的核心在于核方法對PCA的非線性推廣，能有效捕捉數據的非線性特征，主要用于人臉識別、手寫體數字去噪、機器學習、模式識別、數據壓縮、圖像去噪、語音信號處理和函數逼近等領域［11，17-18］。

Kernel_PCA算法的實現過程如下：

對于一般的PCA方法，即通過求解特征方程獲得貢獻率最大的特征值及與之相對應的特征向量：

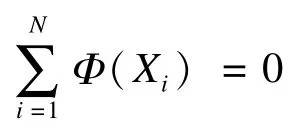
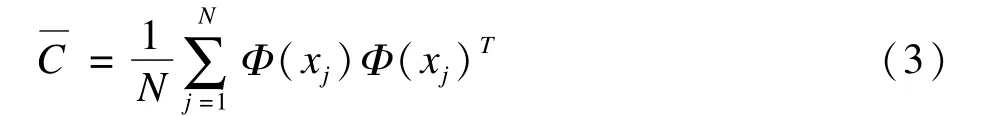
在特征空間中的PCA是求解下列方程的特征值和特征向量，代入式（2）中得：

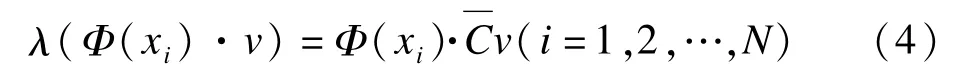
由于特征向量可以由數據集線性表示，則v可以由Φ（xk）（k＝1，2，…，N）線性表示，即：

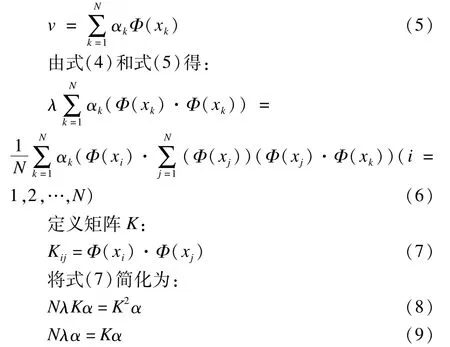
通過對式（9）的求解，即可獲得要求的特征值和特征向量。

綜合評估實現過程

1．實現步驟

根據上述思想路線，給出中醫藥項目的Kernel_ PCA算法綜合評估方法和步驟：

Step 1.將全國15個省份按1，2，…，15依次編號，將2011年到2015年中醫藥項目的所有中醫藥子項目按1，2，…，8依次編號，表中數據項代表的是中醫藥項目的預算執行率（為方便數據處理，全部用0～1的數表示），將原始數據簡化為5張只含有數值和編碼的表。

Step 2.剔除所有項目都缺失的省份以及數據缺失大半的項目，將剩下省份、項目重新依次編號。通過多重填補法處理部分省份部分項目因無預算而缺失的數據，得到一系列完整數據集。

Step 3.將若干個完整數據集采用Kernel_PCA算法進行處理，得到相對應的若干組結果。

Step 4.為消除結果中正負值相互抵消的影響，根據每組結果進行評估排序，得到相應的若干組排序值（無正負）。

Step 5.經計算得到每組排序值的求和平均值，最終得到一組數據，再進行排序，則最后得到的一組數據就能反映全國各省中醫藥項目的綜合評估情況。

2．數據處理

根據需要搭建相應的平臺環境，利用Excel 2010、MATLAB（R2014a）和SPSS 19．0分析工具，對原始數據進行加工、處理等適當操作得到最終結果，如圖1所示：

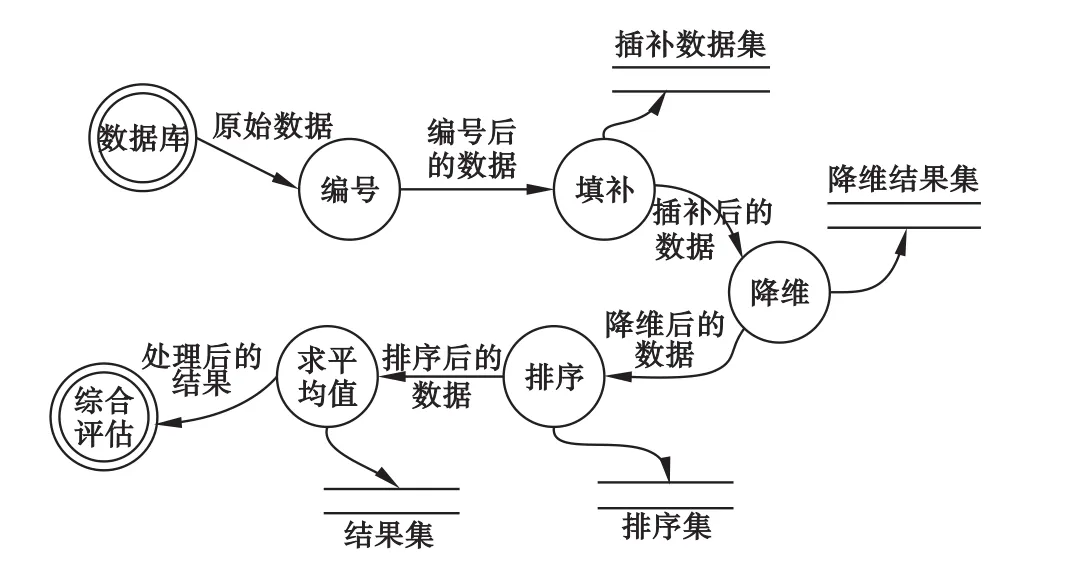
圖1 數據流圖

表1是利用SPSS 19．0分析軟件來對編碼后的數據進行多重填補，采用的是MCMC填補方法，根據對數據的分析處理以及其他學者對缺失值方法對比研究得出的一致結論：M I優于EM、回歸插補法等方法，采用M I方法填補數據，再按照實現步驟中的step3～5，對每個由降維算法得出來的結果進行排序，得到結果如表2所示。

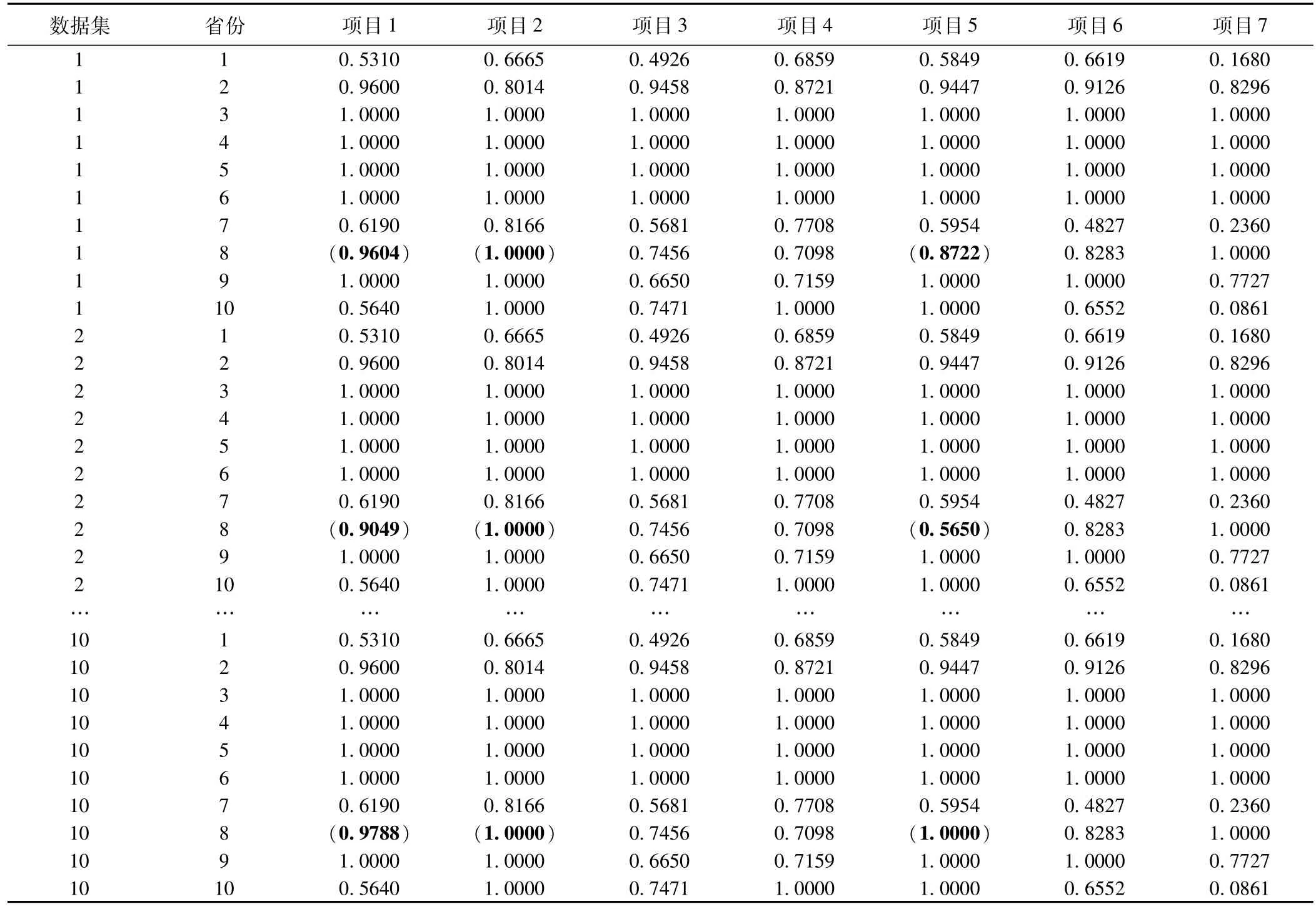
表1 2014年中醫藥項目插補數據集

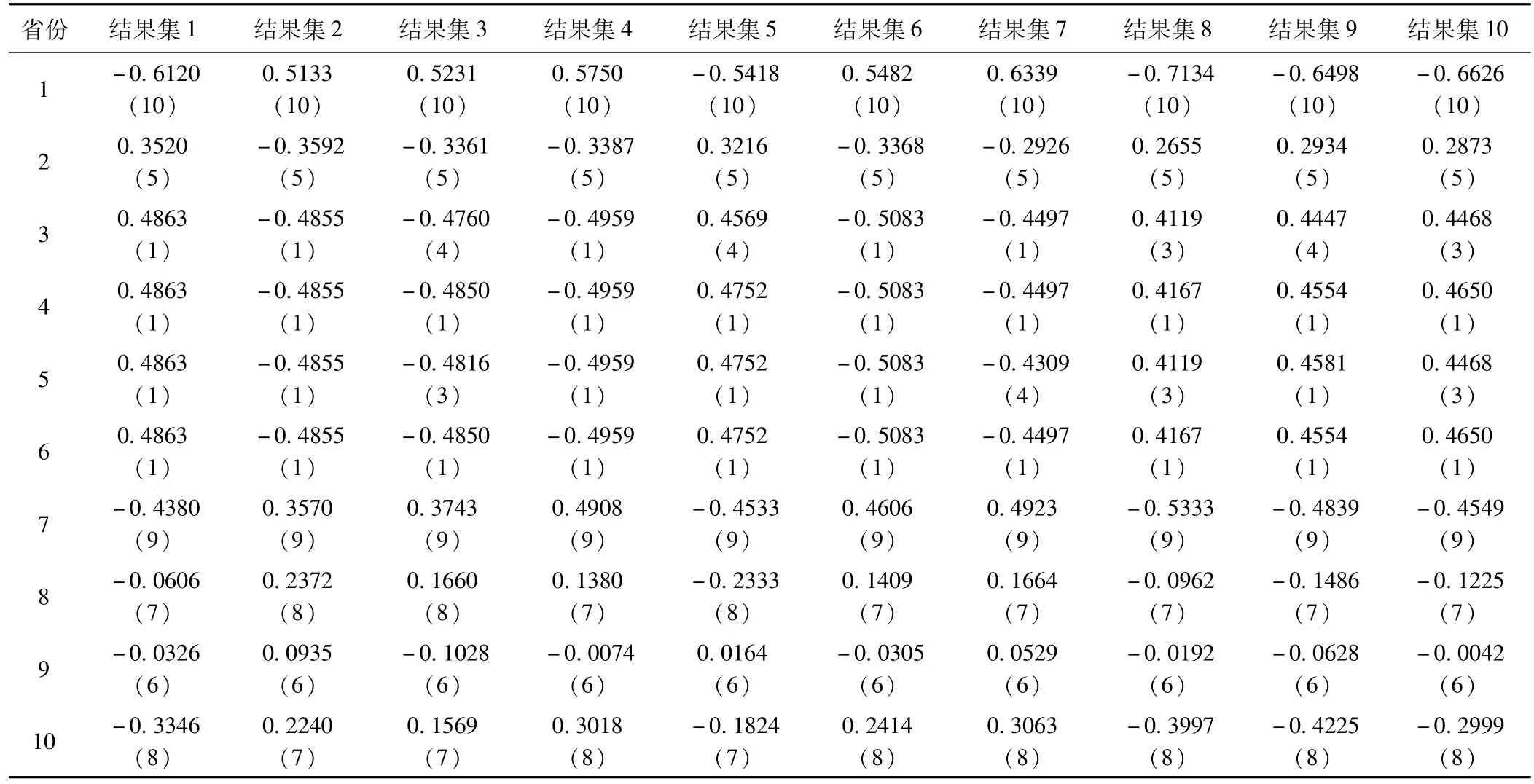
表2 2014年中醫藥項目降維結果集（排序集）

3．綜合排名

根據表2計算出2014年各省總排名，同理可計算出其他年份各省總排名，得到最終結果如表3所示：

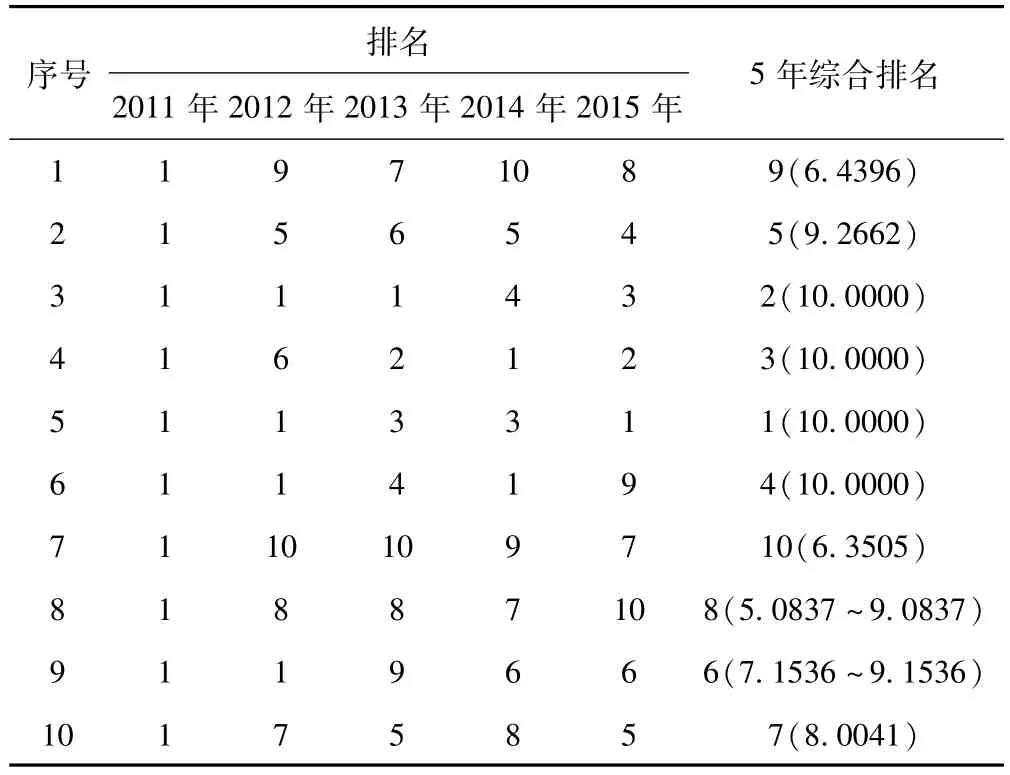
表3 2011-2015年中醫藥項目綜合評估表

結 果

從表3可知，本文評估方法綜合了所有中醫藥子項目的結果，最終認為編碼為3、4、5、6省份的中醫藥項目綜合執行情況較好，數據處理結果與現實情況（由執行率可知，編碼3、4、5、6省份的執行率之和均為10．0000，執行情況較好；編碼1、7省份執行情況較差）基本保持一致，證明了該研究思路的合理性、有效性和準確性［19-20］。

討 論

本文提出基于Kernel_PCA算法的中醫藥項目綜合評估，采用M I進行數據填補，這是經過處理分析選擇的方法（筆者還采用了條目均數填補法、自身均數填補法等方法，比較而言，M I處理的結果更接近完整數據的分析結果，由于篇幅限制，本文對其他方法不展開過多闡述），然后利用非線性數據壓縮特征空間維數的特性，綜合了所有中醫藥子項目的復雜執行情況，能較好地全面反映全國各省中醫藥項目執行情況的差異和中醫藥項目整體情況，避免目前用于中醫藥項目評估的方法單一導致結果片面性較強，不利于對中醫藥項目的整體把握。因此本文探索新方法進行分析，更好地為中醫藥項目決策提供科學依據。基于Kernel_PCA算法綜合評估的最終結果也與實際判斷一致，表明該方法思路的有效性、可行性，可進一步推廣到其他相關項目的綜合評估。

［1］劉晶．中醫藥項目經費預算執行監控通報平臺的分析與設計．湖北中醫藥大學，2012：82．

［2］黃橙紫，王振宇，田雙桂，等．中醫藥項目績效管理現狀與對策探析．中醫藥管理雜志，2014，33（12）：1969-1971．

［3］田雙桂．中央轉移支付中醫藥項目預算執行分析和對策研究．湖北中醫藥大學，2014．

［4］Duan YJ，Lv YS，Kang WW，etal．A Deep Learning Based Approach for Traffic Data Imputation．Proceedings of 17th International IEEE Conference on Intelligent Transportation SystemsⅡ．2014．

［5］Wang Y，Zhang ZC，Tian ZX，et al．Preprocessing the M issing Data for Environmental Prediction Model Based on Multiple Imputation．Proceedings of 2012 International Conference on Power Electronics Engineering and Computer Technology（PEECT 2012）．2012．［6］Li L，Su XN，Zhang Y，et al．Traffic Prediction，Data Compression，Abnormal Data Detection and M issing Data Imputation：An Integrated Study Based on the Decomposition of Traffic Time Series．Proceedings of 17th International IEEE Conference on Intelligent Transportation SystemsⅠ．2014．

［7］帥平，李曉松，周曉華．缺失數據統計處理方法的研究進展．中國衛生統計，2013，30（01）：135-139．

［8］王睿，馬修強，陸健．Epworth量表中缺失數據處理方法研究．中國衛生統計，2013，30（01）：72-73．

［9］佟昕，高強．統計學中的數據缺失及解決方法．遼寧經濟管理干部學院（遼寧經濟職業技術學院學報），2011（02）：15-16．

［10］鄒莉玲，吳娟麗，李覺．多重填補法在任意缺失隨訪資料中的應用．中國衛生統計，2015，32（02）：221-223．

［11］薛冰．Kernel PCA中核參數優化及應用．西安工業大學，2011．

［12］徐濤，孫彤．基于KPCA的非線性ASM定位方法研究．微電子學與計算機，2010，27（12）：113-116．

［13］劉進，鄧家剛，覃潔萍，等．基于紅外光譜數據的中藥藥性識別研究．時珍國醫國藥，2010，21（03）：561-563．

［14］徐明亮，孫長海，王瑜等．基于主成分分析的決明子電化學振蕩指紋圖譜的評價研究．時珍國醫國藥，2011，22（08）：1858-1859．

［15］Ling A，Yi Z，Ye S．Model Reduction for Spatio-temporal Systems based on KPCA and LS-SVRM．第25屆中國控制與決策會議論文集．2013．

［16］Peng HX，Wang R．Sensor Fault Detection and Identification using Kernel PCA and Its Fast Data Reconstruction．Proceedings of 2010 Chinese Control and Decision Conference．2010：3857-3862．

［17］沈徐輝，羅小平，杜鵬英．基于模糊的改進KPCA方法：第二十九屆中國控制會議，中國北京，2010．

［18］趙英男，王水平，鄭玉．一種基于數值逼近的KPCA改進算法．南京信息工程大學學報（自然科學版），2012，04（04）：362-365．

［19］趙小強，王新明．基于改進核主元分析的TE過程故障診斷．工業儀表與自動化裝置，2010（03）：7-11．

［20］胡淼，董方，田麗娟，等．應用因子分析法探討新型農村合作醫療績效評價．中國衛生統計，2016，33（1）：24-26．

（責任編輯：鄧 妍）

湖北省教育廳人文社會科學研究項目（17Q098）；中醫藥項目績效考核數據分析關鍵算法研究

△通信作者：肖勇，E-mail：15327455586＠126．com