基于ACO的TSP問題研究

王爽瑤 范 爽 王 健 沈镕榮

(合肥工業大學宣城校區商學系 安徽 宣城 242000)

基于ACO的TSP問題研究

王爽瑤 范 爽 王 健 沈镕榮

(合肥工業大學宣城校區商學系 安徽 宣城 242000)

從1991年意大利學者DorigoM等首次提出蟻群算法以來，蟻群算法作為一種自然計算方法，由解決TSP問題開始，從一維靜態優化問題到多維動態優化問題，發展到今天已經相對成熟了，蟻群算法可以用來解決一些尚未找到有效算法的問題，而且蟻群算法還是元啟發式算法(Metaheuristic)，是一種算法框架，可以在其基本思想上針對不同問題做改進從而應用到不同問題上去。

Tsp問題；蟻群算法

一、概述

旅行商問題：假設有一個旅行商人要拜訪N個城市，他必須選擇所要走的路徑，路徑的限制是每個城市只能拜訪一次，而且最后要回到原來出發的城市。路徑的選擇目標是要求得的路徑路程為所有路徑之中的最小值。

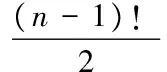
旅行商問題是一個典型的組合優化問題，并且是一個NP難問題，其可能的路徑數目與城市數目n是成指數型增長的，所以一般很難精確地求出其最優解。目前，對TSP問題的研究主要是通過一些啟發式算法，如遺傳算法、蟻群算法、模擬退火算法等，且都取得了一定的成果。

二、基于TSP問題的蟻群算法模型

這里為了讓TSP問題更加的清晰可視，便于基于TSP問題的蟻群算法模型的研究，我們先用數學語言描述TSP。

記G=(V,E)為賦權圖，V=(1,2,…,n)為頂點集，E為邊集，各頂點間的距離為dij，已知(dij>0,dij=∞,i,j∈V)。設當(i,j)在最優回路上，χij取得1值，其他為0，則

則，經典的TSP問題可寫為如下的數學規劃模型

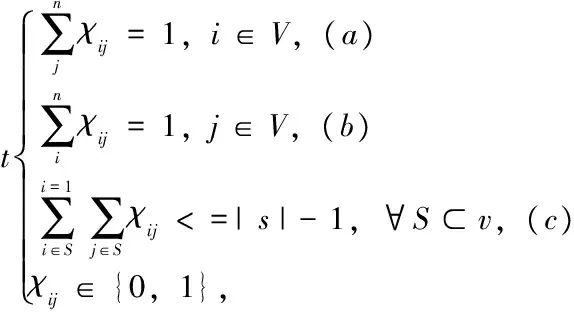
上式中，S的絕對值為集合S中所包含的頂點集。約束(a)和約束(b)意味著對每個點來說，僅有一條邊進一條邊出；約束(c)則說明了沒有任何字回路。于是，滿足上面三個約束條件的解就構成了一條回路。這便是TSP問題的數學表達方式。

根據上述TSP問題數學表達可知，在TSP問題中，城市的數目成為該問題的階數。綜合對比TSP問題和蟻群算法兩者之間各自的特性，通過蟻群算法解決旅行商問題不失為一種相對有效的方式。

根據對TSP問題的分析，結合蟻群算法模型，螞蟻可以按照下列公式選擇下一個訪問的節點：

由上式可知，轉移概率與[τis(t)]α*(ηis(t))β成正比，與真正的螞蟻相比，一個人工蟻群系統有一個記憶內存，為了滿足所有螞蟻必須通過所有城市的約束條件，對于每個螞蟻這里應該要建立一個數據結構，也就是禁忌表，但為了更方便的進行模擬仿真，我們這里建立與禁忌表功能類似的城市數據數組表，記錄在時刻t螞蟻還沒有通過的城市，即：螞蟻在時刻t能夠選擇的下一個城市的集合，在這個循環周期內，螞蟻只能從城市數據數組表中選擇城市進行下一步的轉移。在一個循環周期結束后，城市數據數組表是用來記錄該螞蟻當前所形成的解決方案，即螞蟻所行走的路徑，然后，城市數據數組表將為空值，螞蟻重新選擇行走 路徑。

值得注意的一點是，為了防止殘余信息素太多掩蓋了啟發信息，在完成所需要的步驟或完成整個城市之旅之后，要人工對信息素進行更新處理，這種機能類似于人類大腦的記憶。

根據上述提示，在仿真應用上，每次迭代優化前，需要對各個節點上殘留的信息素進行更新，可以參照下列公式進行。

τij(t+n)=(1-ρ)·τij(t)+Δτij(t)

上式中，

Δτij(t,t+n)表示本次循環中路徑(i，j)上的信息素增量；

值得注意的是，對于信息素的增量Δτij(t,t+n)，我們采取的是蟻量算法，即：

其中Lk表示第k只螞蟻在所走的路徑長度。

三、算法步驟

Step1 初始化參數：初始化螞蟻個數，α、β、ρ、Q，最大循環次數，當前較優解、最優解

Step2 輸入每個城市的名字和坐標，根據坐標計算兩兩城市間的距離，并將所有螞蟻置于起點城市

Step3 重復Step4～Step7，直至最大迭代次數

Step4螞蟻從存有城市狀態的數組里搜索，從起點城市開始，利用狀態轉移函數先計算出選擇下一個沒有去過城市的概率，然后利用輪盤隨機選擇下一個出發城市。當螞蟻走完所有城市的時候，計算整條路徑的距離，并保存螞蟻在兩兩城市間新留下的信息素。

Step5 每一只螞蟻重復Step4，直到一組的所有螞蟻走完所有城市

Step6 將每組螞蟻的較優解保存在數組里，并利用信息素更新規則更新信息素。

Step7 迭代次數n+1

Step8 在保存較優解的數組里找出最優解，輸出每次的較優路徑及長度到控制臺，輸出最佳路徑及長度到控制臺

王爽瑤(1996.07-)，女，漢族，重慶人，合肥工業大學宣城校區商學系，2014級本科生，研究方向：物流管理。