利用光纜標定數據快速進行故障定位

申圣++李晨琛

[摘 要]在WGS84坐標體系下，人們知道地球上兩點的坐標，就可以計算出兩點間的距離。通過光纜標定工作，人們可以掌握光纜的坐標數據，利用標定的光纜數據，知道光纜故障點距離起點的距離，再通過比對點與點之間距離，就可以較為精確且快速地得知故障點所在的坐標范圍，減少光纜故障維護的響應時間。

[關鍵詞]光纜坐標數據；定位；故障點

doi：10.3969/j.issn.1673 - 0194.2017.16.091

[中圖分類號]TN913 [文獻標識碼]A [文章編號]1673-0194（2017）16-0-02

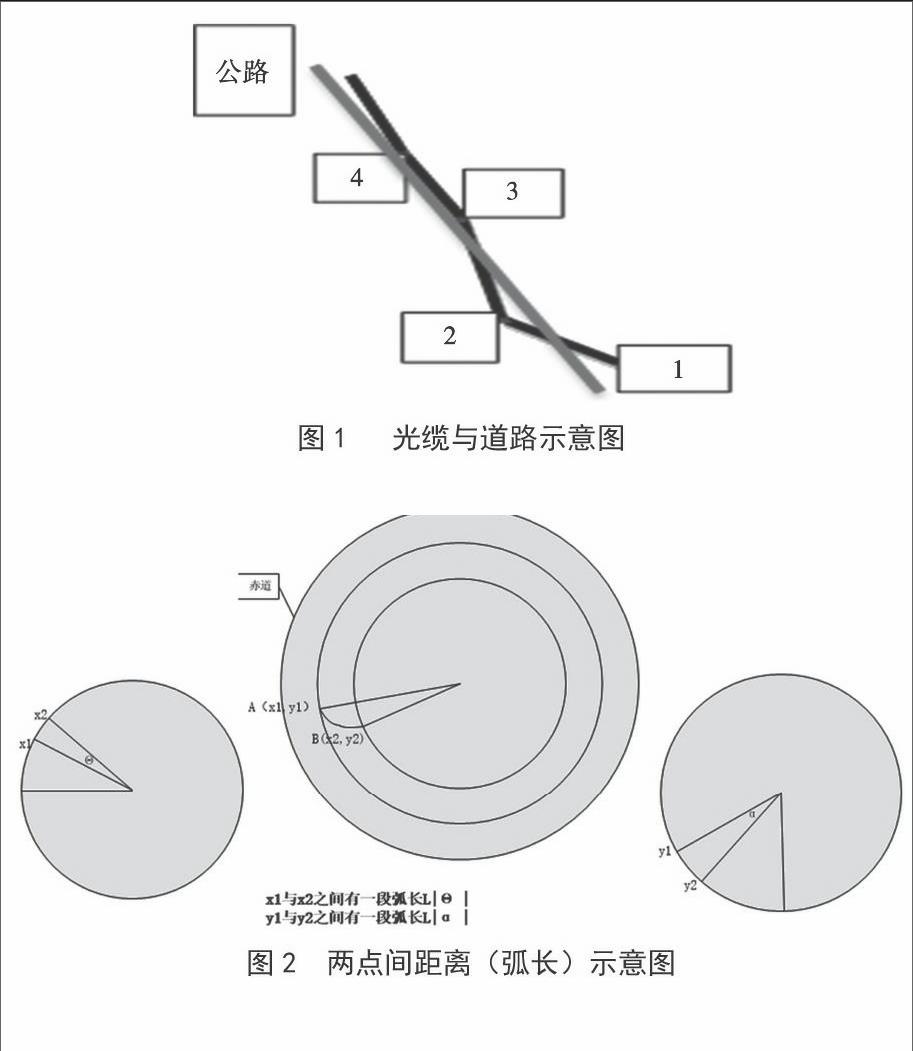
在日常工作中，人們經常會遇到這樣的問題，那就是光纜斷了，但是斷在哪里了？OTDR可以測試出起點到斷點的距離，但是這個距離是否就是路途的距離？地埋的光纜若是斷了，怎么去尋找斷點？光纜如果不是直線，就無法直接得知斷點的地點。如圖1所示。

從圖1可以看出，道路與光纜并非重合，行車路程并不等于光纜長度。盤山路則有可能出現路程長度是光纜長度的兩倍。地埋的光纜若是在春耕期間被挖斷，那么尋找斷點的時間將會被延長。維修人員能夠快速尋找到斷點，就是節省搶修時間、節省人力、物力與財力。本文將從基本操作、計算能力驗證、數據驗證等幾個方面，對故障定位軟件進行說明。

1 故障定位軟件的核心構架

在WGS84坐標體系下，地球可以看作一個球體，其原點為地球質心，所以地球上任意兩點間的距離，可以當作一段弧長來計算。

1.1 計算地球上兩點的距離

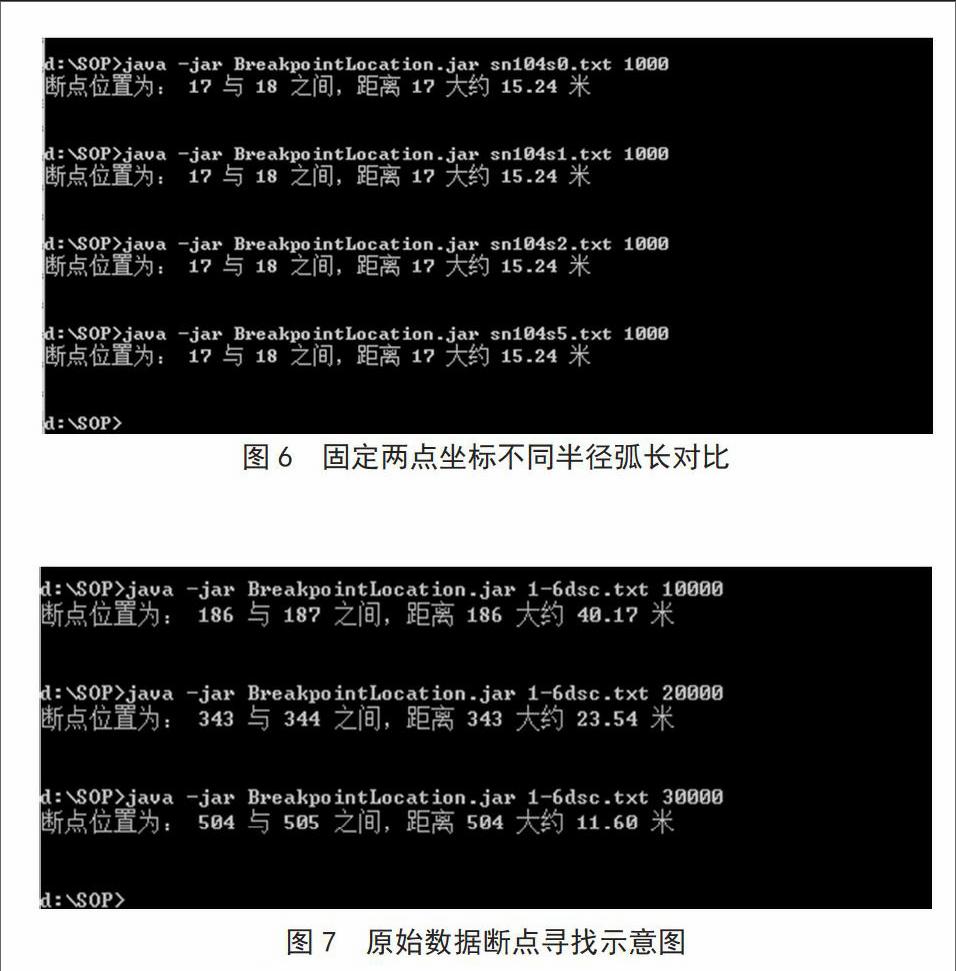
地球上某一點的緯度與經度分別用x與y表示，A點表示為（x1，y1），B點表示為（x2，y2）。如圖2所示。

由圖2可知，AB兩點間的距離為L（A-B），其緯度值差為角θ，對應長度為Lθ；其經度值差為角α，對應長度為Lα。

圓可以看作由無數條短直線構成，而經度與緯度之間又屬于垂直關系，那么由圖3可以得知：

（1）

式中：θ為緯度差值，α為經度差值，L為長度。

1.2 計算兩點間光纜的長度

高度差與L（A-B）圍成一個直角三角形，此段纜長成為一個斜邊，據此可以算出兩點之間纜長距離。

在軟件得到點數據后，人們通過輸入斷點在光纜上的長度，公式會不斷將兩點間的距離相加，并與輸入的數值做比較，直到得出結果。

2 球體半徑對弧長的影響

由圖5可以看出，弧線長度與弧線半徑有關，所以驗證不同球體半徑值下對軟件計算弧長距離的影響。

由圖6可以看出，R在0至5 000米內的距離上，計算相對地球6 371千米的半徑而言，隨著0至5 000米的半徑增加，不影響弧長距離。

3 數據驗證與誤差分析

3.1 數據驗證

取樣為某段坐標數據，此數據的高度值為最低點1 230米、最高點1 362米，趨勢是先低再高，起點高度1 362米、尾點高度1 326米，差值分別為132米與36米。高差均值計算后為1.431米。距離設定為10 000米、20 000米、30 000米。

原始數據在上述長度舉例下的所求得值：

當高差為0的時候：

由圖8與原值圖7相比，不同距離的誤差分別為：4.03米、83.68米、90.9米。

由軟件計算截圖可以看出，在高度差不斷加大的情況下，點數誤差值也會隨之增長。誤差值是否在可接受的范圍內，則需要通過實際驗證，積累更多的反饋信息才能得到結果。

3.2 高差值與其他引起結果誤差的條件分析

3.2.1 預留光纜的誤差

第一，標記的點一般自站外開始，那么自站內光纜托盤到第一個點的距離成為第一段誤差值。

第二，架空與地埋光纜均會有不同長度的預留，是第二個誤差值來源。

3.2.2 其他誤差

架空光纜由于桿子埋深不同，會造成一定程度上的數據偏差。此外，GPS也會在標定中產生一定程度上的誤差。

3.3 關于建立數據庫以減小誤差的設想

人們建立點距離值數據庫能夠減小數據庫誤差。現有數據均為點坐標模式，將點坐標計算轉換為兩點間距離的數據，將光纜預留長度作為兩點間距離的補充長度，直接加入到兩點距離，即將程序不斷提取出兩點的坐標進行距離計算并相加，轉為程序不斷提取出兩點間的距離并相加，從而解決實際使用過程中的光纜預留誤差，而且可以提高程序的運行速度。

4 關于故障定位軟件的后續建議

第一，該軟件要與地圖相結合，尋找到斷點后在地圖上顯示。

第二，開發者通過建立數據庫，并整合軟件，形成更方便的可視化界面軟件。

主要參考文獻

[1]徐紹銓，張華海，楊志強.GPS測量原理及應用[M].武漢：武漢大學出版社，2008.

[2][美]埃克爾.Java編程思想[M].陳昊鵬，譯.北京：機械工業出版社，2007.endprint