平移法解決因動點產(chǎn)生的平行四邊形問題

徐辛炎

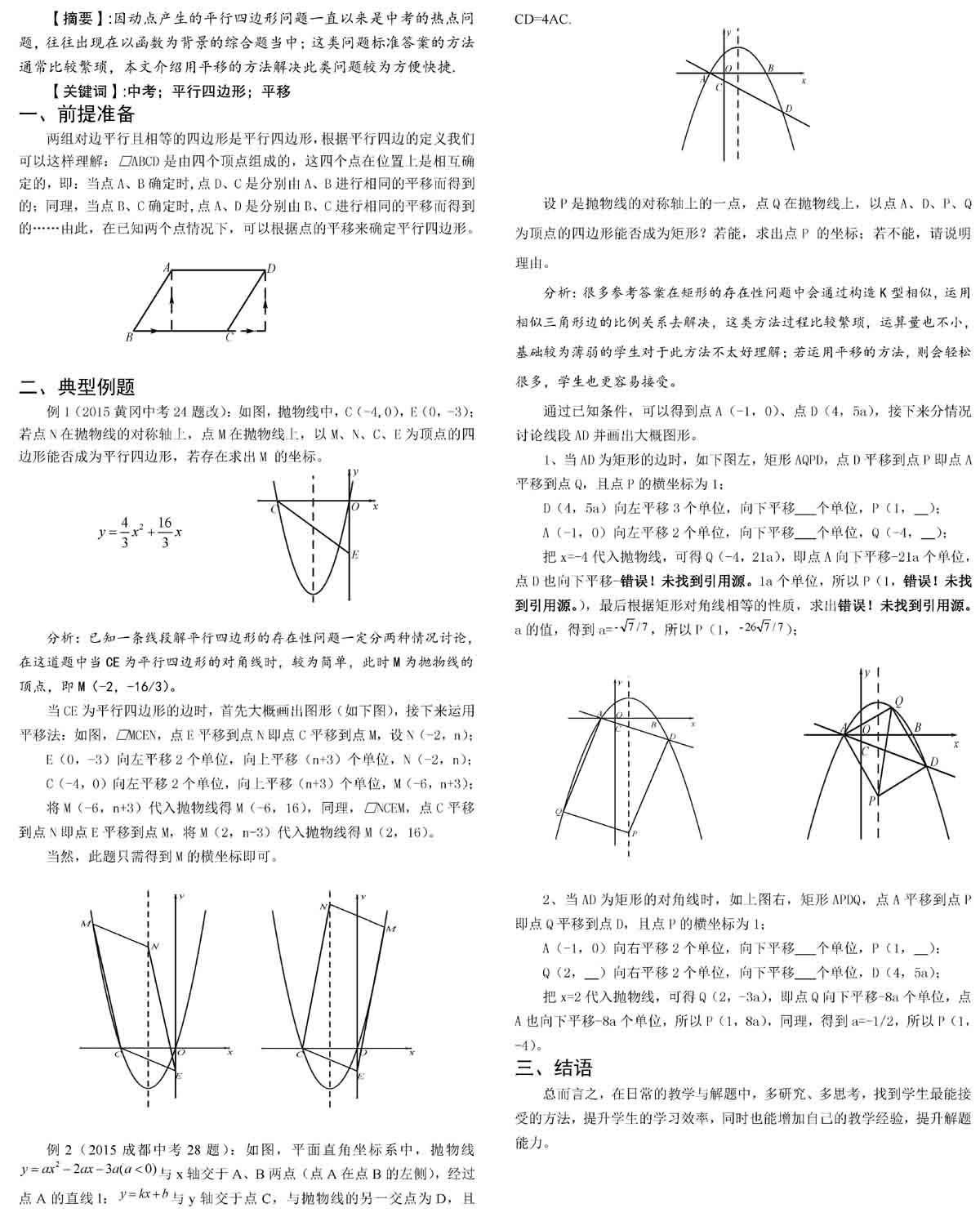
兩組對邊平行且相等的四邊形是平行四邊形，根據(jù)平行四邊的定義我們可以這樣理解：□ABCD 是由四個頂點組成的，這四個點在位置上是相互確定的，即：當點A、B 確定時，點D、C 是分別由A、B 進行相同的平移而得到的；同理，當點B、C 確定時，點A、D 是分別由B、C 進行相同的平移而得到的……由此，在已知兩個點情況下，可以根據(jù)點的平移來確定平行四邊形。

分析：已知一條線段解平行四邊形的存在性問題一定分兩種情況討論，在這道題中當CE 為平行四邊形的對角線時，較為簡單，此時M 為拋物線的頂點，即M（-2，-16/3）。當CE 為平行四邊形的邊時，首先大概畫出圖形（如下圖），接下來運用平移法：如圖，□MCEN，點E 平移到點N 即點C 平移到點M，設N（-2，n）；E（0，-3）向左平移2 個單位，向上平移（n+3）個單位，N（-2，n）；C（-4，0）向左平移2 個單位，向上平移（n+3）個單位，M（-6，n+3）；將M（-6，n+3）代入拋物線得M（-6，16），同理，□NCEM，點C 平移到點N 即點E 平移到點M，將M（2，n-3）代入拋物線得M（2，16）。當然，此題只需得到M 的橫坐標即可。

總而言之，在日常的教學與解題中，多研究、多思考，找到學生最能接受的方法，提升學生的學習效率，同時也能增加自己的教學經(jīng)驗，提升解題能力。