保險產品設計的數學模型

高婷婷， 張明會

(隴南師范高等專科學校初等教育學院， 甘肅成縣 742500)

保險產品設計的數學模型

高婷婷， 張明會

(隴南師范高等專科學校初等教育學院， 甘肅成縣 742500)

在已知投保人恰好k歲死亡的概率為pk的前提下，以保險金本息和余額為隨機變量X，建立了保險公司收益的數學期望Em(X)=∑k∈Λxkpk的概率模型．并給出了在投保人都是恰好滿m歲死亡時，保險公司收益的數學期望的表達式，討論了保險公司不盈不虧(即保險公司收益的數學期望Em(X)=0時)的概率p(Em(X)=0)．通過考慮年齡別死亡率等一些有用的數據，討論了確定合適的a，b，d和n值的一些思路和方法．

概率模型；概率分布列；數學期望；均勻分布

1 問題的提出和復述

某保險公司擬設計一款新產品， 其思路是：投保人從一出生開始， 每月交納固定費用a元， 交滿n年(n是正整數)后停止交費， 并從下一個月開始按月領取固定額度的工資b元， 直到投保人死亡.

為簡單起見， 我們不需要考慮其他例外情況. 假設銀行的月利率為c， 且一直不變. 保險公司只將投保人的交費及時存入銀行， 不進行其他投資.

由于人的死亡具有一定的隨機性， 若已知投保人恰好k歲死亡的概率為pk， 試建立合理的數學模型， 并解答如下的問題.

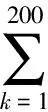
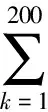
問題4： 從直覺上知道，a,n越小，b,d越大， 投保者越多. 但也可能使公司的風險增大. 根據以上模型， 探討如何確定合適的a,b,d,n(可以引入以上沒有提及的影響因素).

2 模型的假設與變量說明

為了簡化模型， 便于討論和計算， 現對模型中的變量和符號進行說明， 并做一些合理的假設.