巧用解析法，完美向量題

江蘇省如皋市第二中學 楊 芳

巧用解析法，完美向量題

江蘇省如皋市第二中學 楊 芳

向量題一直是高考中的熱門，其中對于向量數量關系的考查已經逐漸成為向量試題中的一個重點，在求解向量題的過程中，學生們常常會遇到好多較為怪異的向量題，這類題如果按照常規的解題思路處理起來，將顯得十分復雜而更為抽象。為此，通過多年的教學分析，我發現轉化思維角度，建立坐標系，將向量幾何化運算轉化為向量代數化運算，巧用解析法，將會是求解向量題的一招妙計。

高中數學；解析法；向量問題

所謂解析法，就是通過分析問題中的各要素之間的關系，用最簡潔的語言或者形式化的符號表達出來，得出解決問題的表達式，順勢求解問題。這種方法在向量問題中的應用較為廣泛，并且能夠幫助學生們降低解題難度，打開自己的思路，提高解題效率，建立妙解向量題的信心。對此，本文將舉例說明解析法在向量題中的應用，與學生們一起探討與總結。

一、巧用解析法，求解向量數量積

在求解向量題過程中，經常會遇到向量的數量積問題，學生們如果在所給圖形中很難求解出相關向量的模及其夾角，那么學生們就要清晰地知道，數量積的運算從幾何層面上求解會有難度，此時就可以運用解析法，建立坐標系，將相關點用坐標表示出來，那么解題就會容易得多，正確率就會有所保障。

解析：根據題意，可以以A為坐標原點，AB所在直線為x軸，AD所在直線為y軸建立如圖所示的坐標系，因此，我們可以得出點A（0,2）、，設F（x，2）有解得x=1，因此，故。

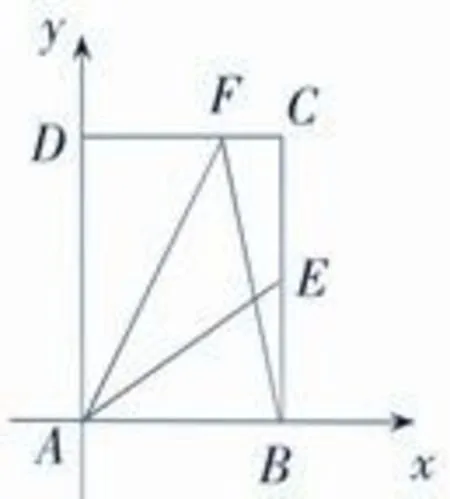
二、巧用解析法，求解向量最值

學生們都知道數學的解題存在著較大的靈活性，究其根本就是命題的連續轉化，在向量的求解過程中，難免會碰到有關求解向量的最值問題的情況，在求解這類題時就可以運用解析法，通過建立坐標系，將其轉化為求函數最值或者求不等式的最值的情形，往往會撥云見日，更加容易解決。

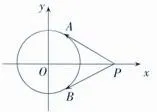
例2 已知圓O的半徑為1，PA、PB為該圓的兩條切線，A、B為兩個切點，那么的最小值為多少？

解析：根據題意，建立如右圖所示的坐標系，于是可以寫出圓O的方程為，此時可設、那么從而得即又因為，所以，故因此，那么，當且僅當時取等號，即的最小值為

點撥：本道題通過建立坐標系，讓解題變得更加直觀明了，借助解析法順利地求解，而如果運用向量的數量積定義去求解的話，∠APB的余弦值用AP表示， 那么求解過程就會很煩瑣，正確率也會有所降低。

三、巧用解析法，求解參數值

在求解向量的過程中，我們往往會遇到向量題中含有參數的情形，并且最后需要求解這個參數，學生們拿到這樣的題，就需要仔細觀察分析，盡可能地去建立關于參數的方程來求解，把幾何問題代數化，向量問題坐標化，方能巧妙化解向量難題。

例3 已知△ABC為等邊三角形，AB=2，設點P、Q滿足，若試求的值。

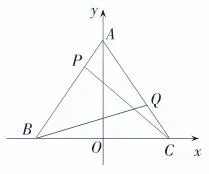
點撥：本題是向量中求解參數類題型，通過建立坐標系，把向量用坐標表示出來，思路清晰，同時用坐標系更加直觀地反映出幾何與代數之間的關系，有利于培養學生們數形結合的意識，鍛煉學生們的思維能力。

總之，通過對以上例題的分析，相信學生們對于解析法在向量題中的應用有了更深的認識，相應的向量應用還有許多，這就需要教師們在教學中不斷灌輸，學生們認真學習，努力實踐，在解題中靈活運用，才能感受解析法的益處。