關(guān)于高中不等式的解題方法與技巧探析

楊 瓊

?

關(guān)于高中不等式的解題方法與技巧探析

楊 瓊

（湖南省永州市第四中學(xué) 湖南 永州 425000）

在高考數(shù)學(xué)試題當(dāng)中，不等式方面的考題一直都是重點考查的一個問題，同時也是歷年高考考查的熱點話題。不等式方面的試題多數(shù)都以解答題這種形式出現(xiàn)，無論是高考試題或是日常考試當(dāng)中，不等式有關(guān)試題都會出現(xiàn)，這足以看出不等式這一知識點的重要性。通過對不等式相關(guān)試題的考查，能夠?qū)忌季S能力及解題能力加以考考查。因此，高中教師需要指導(dǎo)學(xué)生對不等式相關(guān)解題技巧以及解題方法加以整理、歸納以及掌握，以期對其學(xué)習(xí)提供一些指導(dǎo)及參考。

高中數(shù)學(xué)；不等式；解題方法；解題技巧

1 借助反證法對不等式有關(guān)問題加以解決

在對不等式加以學(xué)習(xí)期間，學(xué)生常常會遇到一些證明題，也就是給出一些條件，之后在證明一個等式或者不等式是否成立。對于這類題目，多數(shù)情況之下直接證明較為困難，此時就需要學(xué)生轉(zhuǎn)換思維，把直接證明變成間接證明，也就是借助反證法對不等式加以證明。反證法就是當(dāng)通過正面難以對問題加以解決之時，通過對已知條件或者結(jié)論加以相反假設(shè)，之后得出與已知條件的相悖點，這樣可以證明假設(shè)錯誤，而原命題正確。這種方法不僅僅在幾何問題當(dāng)中有著廣泛運用，同時，在對不等式相關(guān)問題加以證明當(dāng)中也有著非常廣泛的應(yīng)用。

解析：這道題如果學(xué)生選擇直接證明會遇到很大困難，很難獲得解題思路，此時學(xué)生可以轉(zhuǎn)變思維，借助反證法加以證明。

2 通過換元方法對不等式有關(guān)問題進(jìn)行簡化

實際上，在小學(xué)階段學(xué)生就已經(jīng)對不等式有關(guān)問題有所接觸，然而到了高中階段之后，不等式有關(guān)問題的種類逐漸增多，而且大部分都和其他知識進(jìn)行結(jié)合考查。在對不等式有關(guān)問題加以求解期間，高中生很容易想到不等式具有的性質(zhì)，然而此種解題方法無法適用于所有問題。針對形式相對，但沒有特點的這類不等式，高中生需要借助解題技巧，對不等式加以適當(dāng)變形，進(jìn)而進(jìn)行求解。因此，數(shù)學(xué)教師在指導(dǎo)高中生對不等式有關(guān)問題加以解決之時，需要將某一式子作為統(tǒng)一整體，通過一個量將其取代，進(jìn)而對不等式有關(guān)習(xí)題加以相應(yīng)簡化，而這種方法就是換元法。

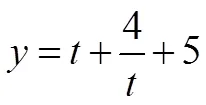
3 借助線性規(guī)劃這種方法對不等式有關(guān)試題加以解決

在不等式有關(guān)問題當(dāng)中，線性規(guī)劃和不等式相關(guān)問題進(jìn)行綜合考查的幾率非常高，高中生在答題期間需要對最小值及最大值加以關(guān)注，同時要注意圖形面積和不等式的定義域這些數(shù)學(xué)知識有關(guān)。因此，教師在指導(dǎo)學(xué)生對問題加以解答之時，需要讓高中生把線性規(guī)劃和不等式有關(guān)性質(zhì)加以掌握，同時把這些知識點進(jìn)行聯(lián)系，這樣才能對答題整體準(zhǔn)確性加以保證[2-3]。

4 結(jié)論：

綜上可知，數(shù)學(xué)教師在實施不等式有關(guān)課堂教學(xué)期間，必須要指導(dǎo)學(xué)生對不等式有關(guān)解題基本規(guī)律加以了解，讓高中生能夠借助反證法、換元法以及線性規(guī)劃來對不等式有關(guān)問題加以求解。同時讓其對不等式有關(guān)解題方法以及解題技巧加以掌握，以此來保證解不等式相關(guān)習(xí)題的具體思路以及邏輯思維整體準(zhǔn)確性。這樣一來，才能對不等式整體解題效率加以提高，進(jìn)而提高學(xué)生數(shù)學(xué)整體考試成績，并且為高中生日后對數(shù)學(xué)知識加以學(xué)習(xí)打下堅實基礎(chǔ)，同時提升學(xué)生數(shù)學(xué)方面綜合素質(zhì)。

[1]戴安妮.高中數(shù)學(xué)不等式易錯題型及解題技巧[J].數(shù)理化解題研究，2017(19)：48-49.

[2]高強(qiáng).高中數(shù)學(xué)不等式部分的易錯題型及解題技巧[J].數(shù)理化解題研究，2016(07)：14.

in the college entrance examination mathematics test question, inequality of examination questions is always focuses on a problem, is also a hot topic in the calendar year college entrance examination examination Inequality in terms of questions most are to answer questions in this form, whether it is a test or routine examination of inequality related to test questions will appear, this inequality is enough to see the importance of the knowledge Through the examination of inequality related questions, to be able to test examines students thinking ability and problem solving ability Therefore, high school teachers need to guide students to inequality related problem solving skills and problem solving methods to use inductive and grasp, in order to provide some guidance and reference to the study

high school mathematics; Inequality; Problem solving method; The problem solving skills

G634.6

A

1672-9129(2017)10-0200-02