直線電機滑臺摩擦特性和摩擦模型

陳 浩, 孟 健, 安 琦

(華東理工大學機械與動力工程學院,上海 200237)

直線電機滑臺摩擦特性和摩擦模型

陳 浩, 孟 健, 安 琦

(華東理工大學機械與動力工程學院,上海 200237)

為了提高直線電機在高速、高加速工況下的運動精度,需要對直線電機滑臺的摩擦特性進行研究。本文通過直線電機實驗臺研究了加速度和速度對摩擦力的影響。實驗結果表明:加速度越大,預滑動階段結尾處的臨界摩擦力也越大;加速度越大,混合潤滑區摩擦滯后現象越顯著,使得Stribeck曲線出現后移;在高速運動下,黏滯摩擦力并不隨速度呈線性變化,黏滯摩擦因子會隨著速度增加而逐漸減小。針對這些摩擦特性,提出了考慮加速度影響的Stribeck二元摩擦模型。結合實驗數據辨識出了模型參數并通過對比其他工況下的實驗數據和模型預測值,驗證了Stribeck二元模型的有效性。

直線電機滑臺; 摩擦特性; 加速度; 摩擦模型

直線電機由于沒有中間傳動環節帶來的誤差,能極大地提高運動精度,同時能實現比“旋轉電機+機械變換環節”的傳動形式大得多的進給速度和加、減速度,所以直線電機得到廣泛應用[1]。直線電機滑臺機構常采用脂潤滑的滾動直線導軌進行導向和支撐,屬于機械接觸式的滑臺機構,摩擦的存在不可避免。所以,必須對直線電機滑臺機構摩擦特性進行研究,并通過建立合理的摩擦模型進行摩擦補償來減少摩擦對直線電機系統運動精度的影響。

Chen等[2]根據直線電機滑臺在預滑動階段和滑動階段摩擦特性的不同,提出了新的摩擦力模型并設計了分段模糊PID控制器。通過仿真和實驗,驗證了所建立的模型和控制器能很好地進行摩擦補償。張叢鵬等[3]根據導軌各處摩擦力的不同,提出了一種基于經典Stribeck摩擦力模型和工作臺運動副位置參數的摩擦模型。譚文斌等[4]根據速度較高時,摩擦力矩隨速度增加其增長趨勢減緩的現象,建立了 LuGre修正模型并通過摩擦補償實驗驗證了LuGre修正模型的有效性。Zhang等[5]對摩擦滯回現象(Friction hysteresis)和黏滑運動(stick-slip)進行了綜述并介紹了幾種研究滾珠直線導軌的摩擦滯回和黏滑的實驗設備,實驗結果表明黏滑運動受到多種因素的共同影響。Cheng等[6]用實驗研究了THK SRG25直線導軌的摩擦力與外載荷、預載、速度、黏度之間的關系并提出了一個摩擦力經驗公式,但公式的參數需要通過實驗獲得。Xi等[7]利用直線電機驅動平臺研究了滾珠直線導軌在預滑動階段的摩擦滯回特性,實驗發現非局部記憶效應(non-local memory effect)和歷史軌跡對預滑動階段摩擦行為有重要影響。Rahmani等[8]研究了導軌的黏滑現象以及在不同預壓載荷下、不同外載荷以及不同運行速度下摩擦力的變化。Fernando等[9]針對直線電機滑臺機構的摩擦滯后(Friction lag)、摩擦滯回等特點,基于GMS摩擦模型,提出了兩狀態GMS改進模型來簡化控制律,通過實驗進行摩擦補償證明了改進模型的有效性。

通過以上文獻分析可知,目前對直線電機滑臺所受的摩擦力與運行條件的關系以及摩擦動態特性已做了很好的研究,但對直線電機滑臺摩擦力與加速度的關系以及在高速下的摩擦特性的研究存在不足。本文在直線電機實驗臺上深入研究了摩擦力與加速度、速度的關系,并根據這些摩擦特性提出了考慮加速度影響的Stribeck二元模型。結合實驗數據進行了模型參數辨識并驗證了Stribeck二元模型的有效性。

1 直線電機滑臺摩擦特性實驗研究

1.1實驗平臺

直線電機實驗臺如圖1所示,主要由PBA system直線電機、科爾摩根驅動器、工控機、Motion Engineering軟件、THK SHS15R直線導軌、雷尼紹光柵尺組成。此款直線電機為U型槽式無鐵芯直線電機,無磁吸力和齒槽力,運動干擾主要來自于直線導軌的摩擦力。直線導軌采用THK公司AFE專用潤滑脂潤滑,此潤滑脂以高級合成油作為基礎油,尿素類作為增稠劑,與普通金屬皂基油脂相比,有著更好的氧化穩定性,但由于潤滑油脂的黏度是影響摩擦力大小的主要因素,所以并不影響本文摩擦實驗現象的普適性。

通過光柵尺和驅動器可直接獲得每一個采樣時刻的位置信號和電流信號。位置信號經過一次差分得到速度信號,經兩次差分得到加速度信號。由于系統存在噪聲,所得速度信號與加速度信號以及電流信號還需經過移動平均法進行濾波降噪處理。摩擦力實驗值通過式(1)間接計算得到。直線電機實驗臺參數見表1。

(1)

其中:Kf為直線電機推力常數;i為瞬時電流;m為直線電機滑臺總質量;a為直線電機滑臺瞬時加速度。

表1 直線電機實驗臺參數Table 1 Parameters of the linear motor experiment table

圖1 直線電機實驗臺(a)和滑臺(b)Fig.1 Linear motor experiment table (a) and linear motor rolling-guide stage (b)

1.2潤滑狀態下摩擦力基本特性

在潤滑狀態下,從靜止開始加速,摩擦力的變化經歷了4個階段(見圖2)。

(1) 預滑動階段(Pre-sliding regime)。此階段速度近乎零,摩擦力主要來自于接觸面上關聯結(Asperities)的彈塑性變形,隨著變形位移的增大,摩擦力也持續增加。直至某一時刻,關聯結斷裂,摩擦力從預滑動階段進入宏觀滑動階段,摩擦力有所下降,這期間摩擦力的最大值就是臨界摩擦力(Break-away force)。

(2) 邊界潤滑階段(Boundary lubrication)。此時速度稍有增大,但仍處于低速階段以至于接觸面上只存在幾個分子層厚度的吸附油膜,摩擦力仍以關聯結間的摩擦形成的弱化效應為主。

(3) 混合潤滑階段(Mixed lubrication)。此階段接觸面上已形成部分承載油膜,但關聯結間的弱化效應大于潤滑油的黏性效應,因此摩擦力仍呈現弱化的趨勢即Stribeck效應。

(4) 完全流體潤滑階段(Full fluid lubrication)。此時關聯結間完全不接觸,摩擦力來自于潤滑油的黏性效應,所以此階段的摩擦力會隨著速度的增大而增大[10]。

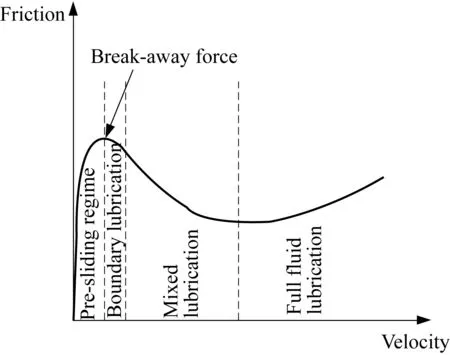
圖2 潤滑狀態下摩擦力的4個典型階段Fig.2 Four typical regimes of friction under lubrication

1.3摩擦力與加速度的關系

為了深入了解加速度對摩擦力的影響,本文共設置了11組不同實驗工況下的摩擦實驗,均為正弦加速度運動軌跡規劃(見表2)。

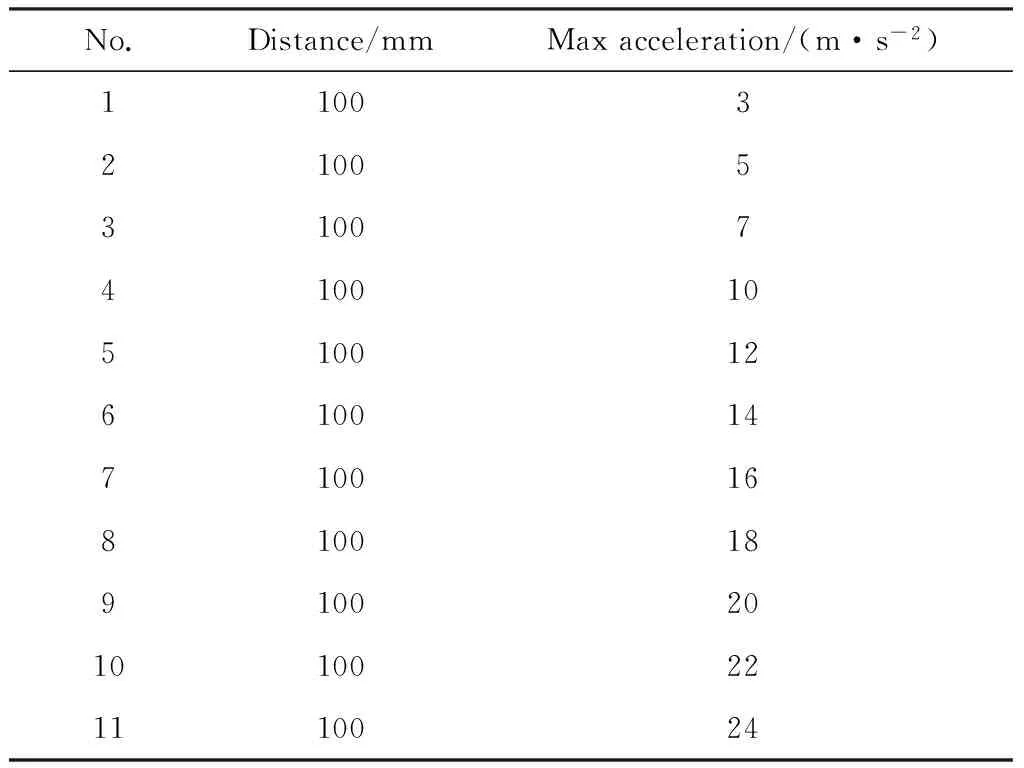
表2 實驗工況安排Table 2 Experimental arrangement

圖3(a)為表2實驗工況下摩擦力-速度-加速度的三維曲線匯總圖。為了表示清楚,在圖3(a)中只畫出了第1、3、5、7、9、11組實驗工況下的摩擦力曲線圖。圖3(b)為圖3(a)前視圖局部放大圖。圖3(c)所示為11組實驗工況中摩擦力在預滑動階段結尾所達到的臨界摩擦力與其瞬時加速度的關系。

從圖3(a)、圖3(b)看出,對于同一條曲線,加速時混合潤滑區出現了明顯的Stribeck效應,減速時混合潤滑區卻幾乎沒有出現Stribeck效應。對比不同實驗工況下的摩擦曲線發現,加速段的加速度越大,在混合潤滑區,摩擦滯后現象越顯著,使得Stribeck曲線出現了明顯的后移。

從圖3(c)看出,在預滑動階段,加速度越大,預滑動階段結尾所達到的臨界摩擦力也越大,直至穩定在一個定值附近。

1.4摩擦力與速度的關系

在研究摩擦力與速度的關系中,為了消除加速度對摩擦力的影響,本文主要是通過比較不同常速運動下的摩擦力進行研究。通過實驗獲得了不同勻速運動速度下的平均摩擦力值,得到了摩擦力和其勻速運動速度關系曲線(圖4)。

由圖4可以看出,在低速下,存在典型的Stribeck效應,但進入以黏滯摩擦為主的完全流體潤滑區域后,黏滯摩擦力并沒有隨速度的增加一直呈線性上升,速度較高時,黏滯摩擦力上升得越來越慢,即黏滯摩擦因子越來越小。

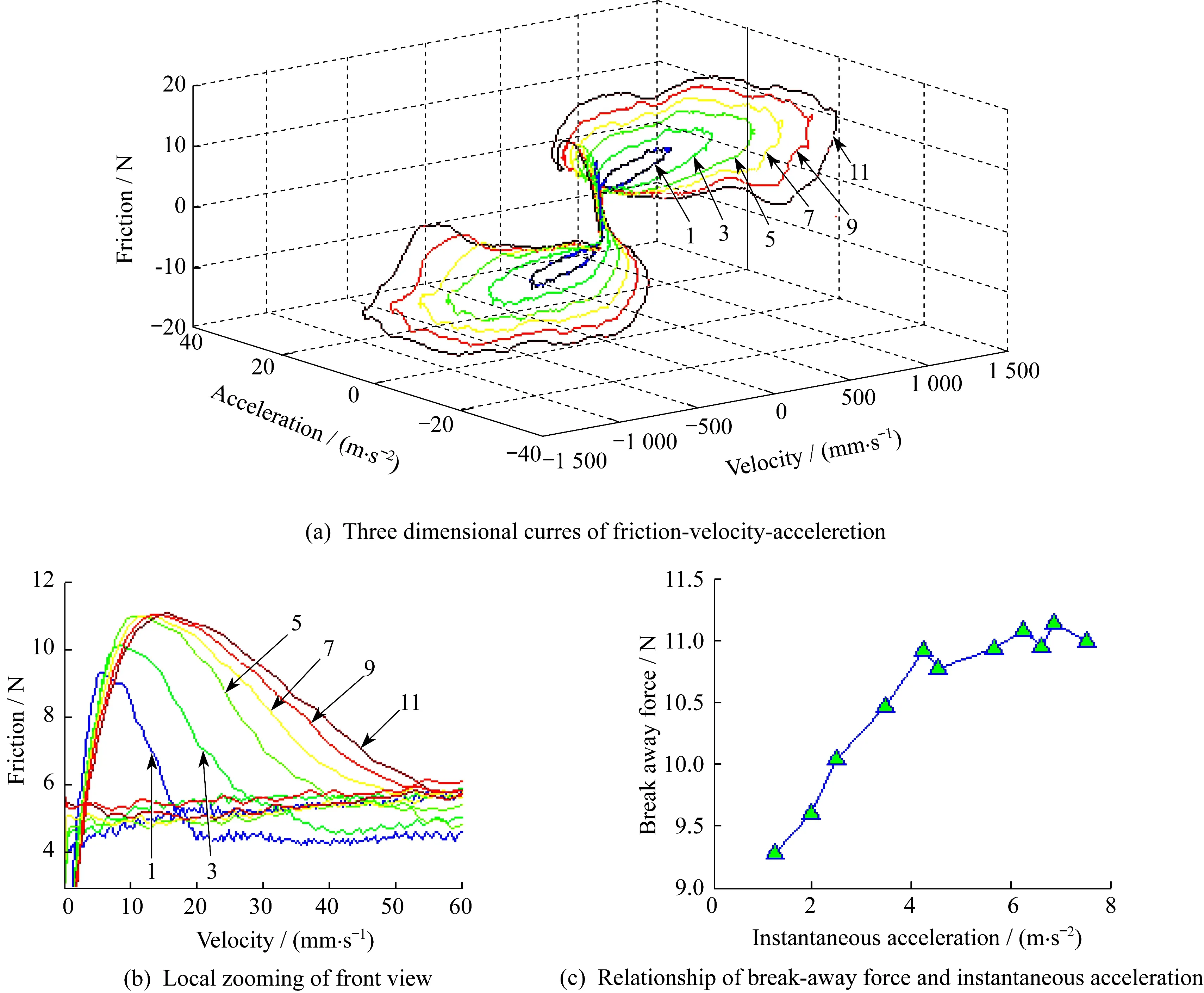
圖3 加速度對摩擦力的影響Fig.3 Effects of acceleration on friction

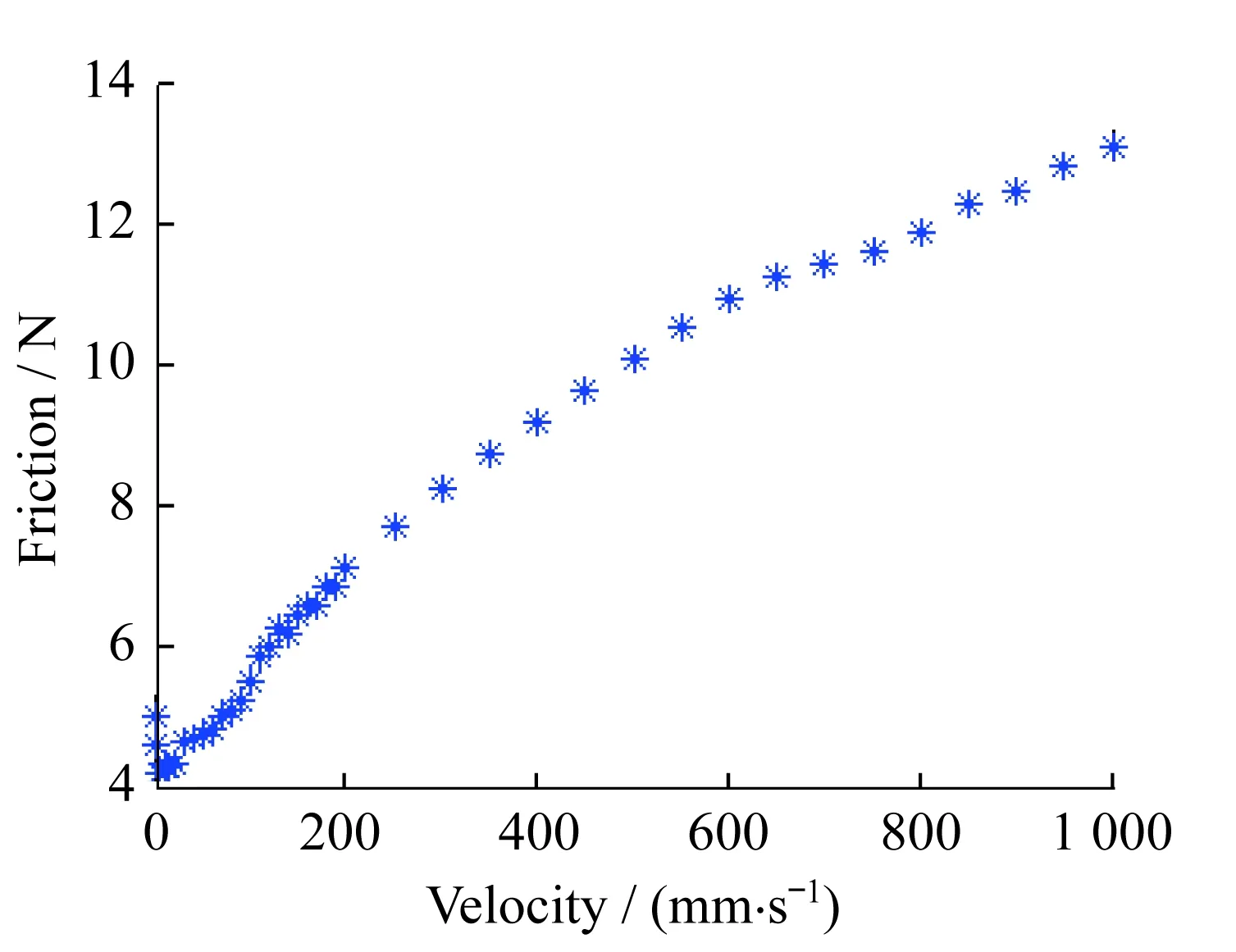
圖4 摩擦力-速度關系曲線Fig.4 Relationship of friction and velocity

2 Stribeck摩擦模型及其改進

2.1傳統的Stribeck摩擦模型

Stribeck[11]最早研究了潤滑條件下,摩擦力在定常速度下的變化情況,發現了Stribeck效應即當克服靜摩擦力之后,摩擦力在低速下隨著速度的增加而減小的現象。Stribeck模型就是考慮了此現象后提出的,模型表達式為

(2)

其中:Fa為外部作用力;Fs為最大靜摩擦力;Fc為庫侖摩擦力;vs是Stribeck特征速度;b為黏滯摩擦系數;δ是經驗常數,如圖5所示。Tustin[12]取δ=1,Bo和Pavelsecu[13]取δ為0.5～1,而Armstrong[14]則取δ=2。

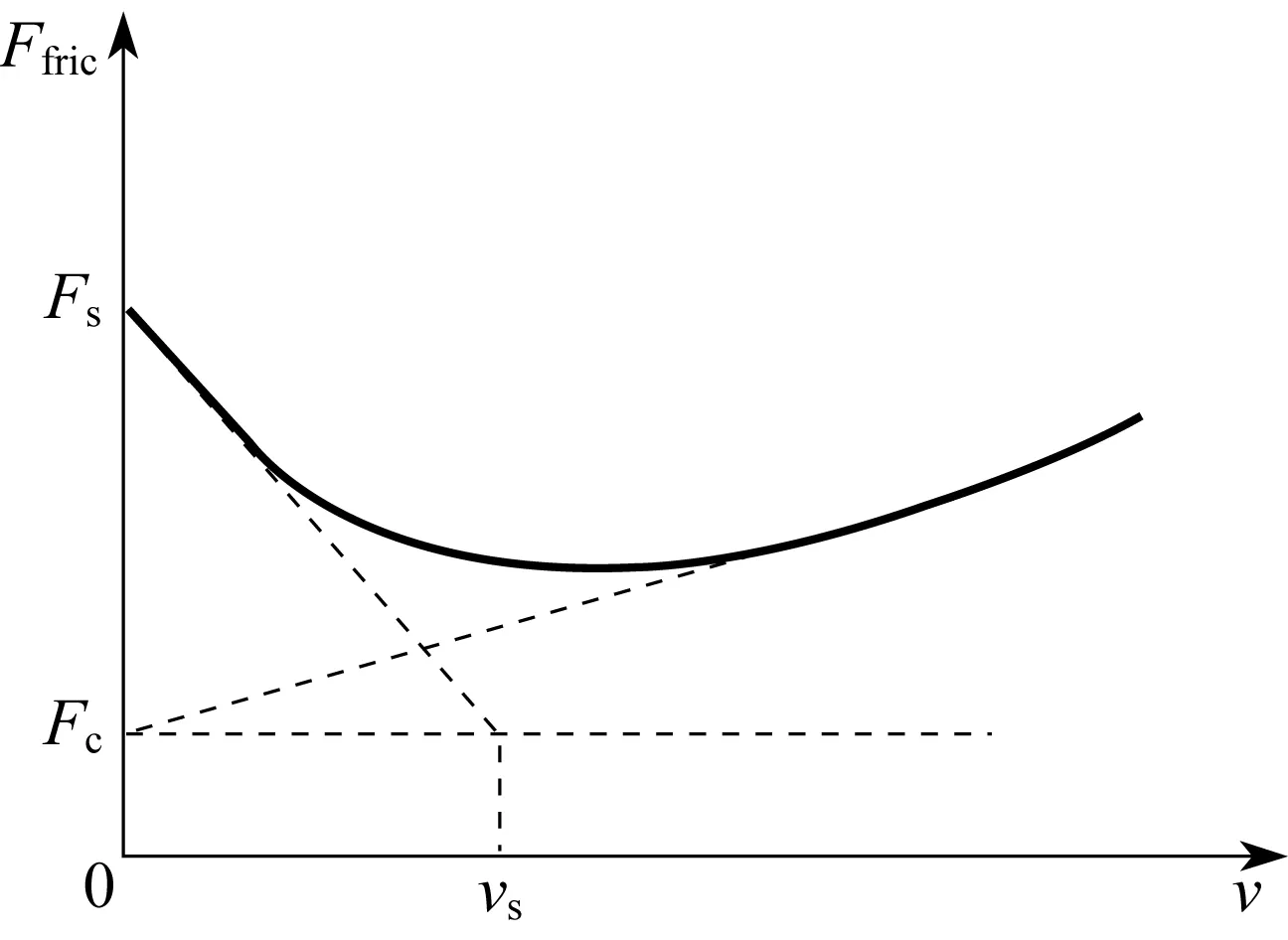
圖5 Stribeck摩擦模型Fig.5 Stribeck friction model

該模型用一個衰減指數項體現了負斜率摩擦現象,很好地描述了低速下的摩擦行為。實驗表明該模型能以90% 的精確度近似擬合真實摩擦力[10]。傳統的Stribeck模型存在以下問題:

(1) 傳統的Stribeck模型在速度零點處是關于速度的不連續函數,且不能描述預滑動階段;

(2) 傳統的Stribeck并沒有考慮加速度對摩擦力的影響,可以認為它描述的是加速度a=0這樣特殊情況下的摩擦力曲線;(3) 傳統的Stribeck模型認為黏滯摩擦力隨速度線性上升,這與高速下的實驗數據不符。

2.2Stribeck二元摩擦模型

根據上面的摩擦特性實驗可知,加速度對摩擦力有很大的影響:加速度增大會造成臨界摩擦力逐漸變大,也加劇混合潤滑區的摩擦滯后現象因而使得Stribeck曲線后移。同時還發現在高速下,黏滯摩擦系數隨速度的增加逐漸變小。為此,本文基于以上摩擦特性,對傳統的Stribeck模型進行改進,提出了Stribeck二元摩擦模型,如圖6所示。

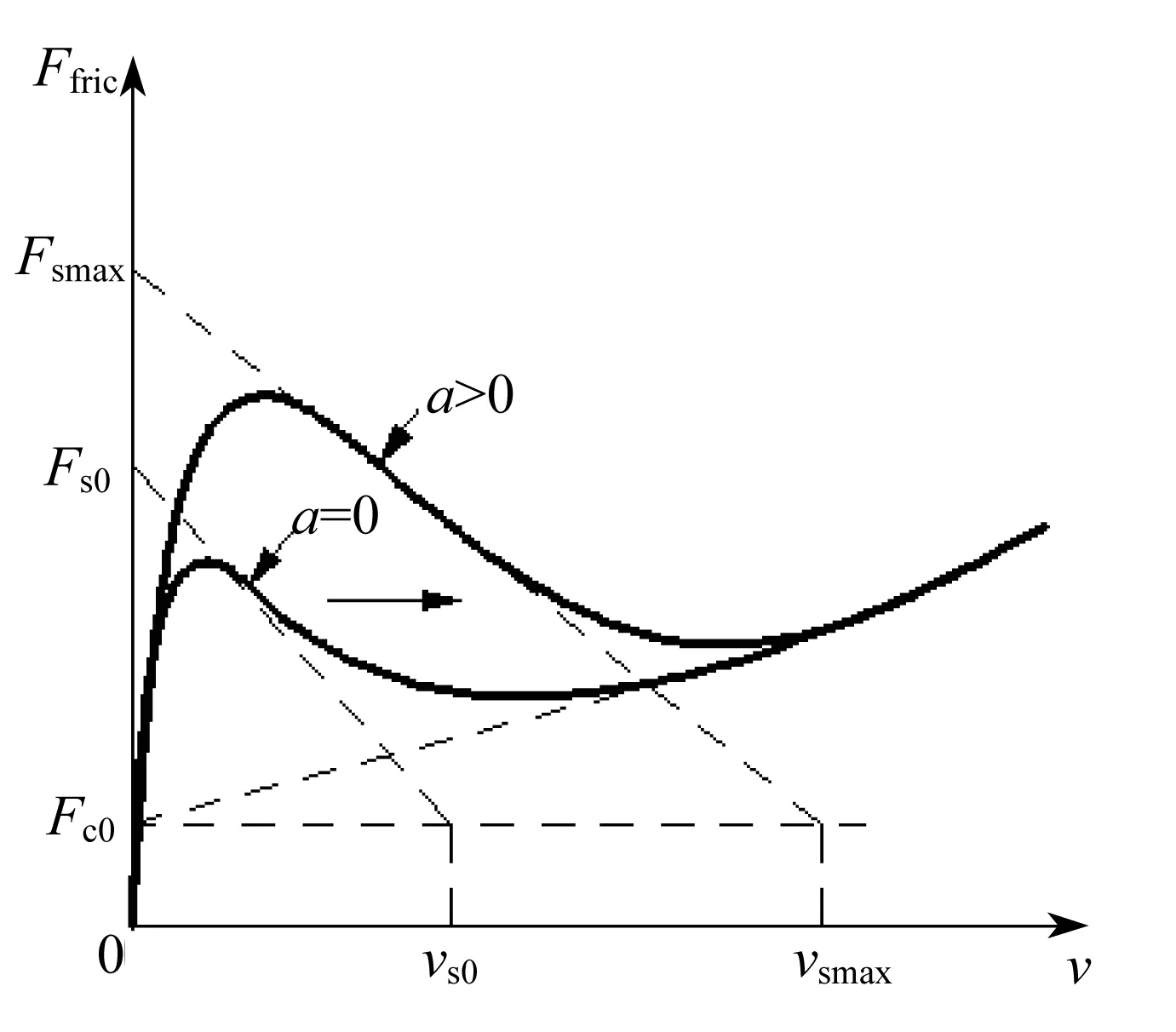
圖6 考慮加速度影響的Stribeck改進模型Fig.6 Modified Stribeck model considering the effects of acceleration

Stribeck二元摩擦模型表達式如下:

(3)

此模型是關于速度v和加速度a的二元函數,包含了9個參數。從圖7中可以看到,Fs0、Fc0、vs0、b1和b2這5個參數是靜態參數,描述的是加速度a=0時的Stribeck曲線,Fs0為此時曲線所對應的最大靜摩擦力,Fc0為此時曲線所對應的庫侖摩擦力,vs0為此時曲線所對應的特征速度,b1和b2為描述黏滯摩擦項與速度的非線性關系的控制參數。Fsmax、vsmax、k1和k2這4個參數是動態參數,描述的是加速度a>0時的Stribeck曲線,Fsmax為在加速度影響下最大靜摩擦力所能達到的最大值,vsmax為在加速度影響下Stribeck特征速度所能達到的最大值,k1為加速度影響下Stribeck曲線后移的控制參數,k2為預滑動階段的控制參數。

相比傳統的Stribeck模型,新模型的變化主要體現在:

(1) 傳統的Stribeck模型中,vs是一個常量,新模型中則將vs改進成關于加速度a的函數來描述加速度變大造成混合潤滑區Stribeck曲線后移的現象。加減速時Stribeck曲線的不同則是通過S(av)來描述。

(2) 傳統的Stribeck模型無法描述預滑動階段,并且在速度零點處并不連續。新模型通過g(v)來描述在預滑動階段,由于g(v)是關于原點對稱的函數,新模型在速度零點處是連續函數。同時可通過g(v)、vs和Fsmax三者的共同作用來描述加速度對臨界摩擦力的影響。

(3) 傳統的Stribeck模型的黏滯摩擦項是關于速度的線性函數,這在速度較高時并不符合實驗現象。為此,新模型在黏滯摩擦項Fvisco中引入速度的指數函數來描述黏滯摩擦系數隨速度的增加而逐漸減小的現象。

2.3Stribeck二元摩擦模型參數辨識

2.3.1 概述 本文采用非線性最小二乘擬合的方法,利用MATLAB中lsqcurvefit函數結合實驗數據進行參數辨識。參數辨識過程分兩步驟進行即靜態參數辨識和動態參數辨識。

2.3.2 靜態參數辨識 靜態參數辨識采用圖4中的實驗數據進行。由于沒有加速度的作用,此時Stribeck二元模型可簡化為式(4)。其靜態參數辨識結果見表3。

(4)

表3 靜態參數辨識結果Table 3 Results of static parameter identification

圖7是基于式(4)的擬合曲線,該擬合的均方根誤差只有0.119 6,說明Stribeck二元摩擦模型對高速下的實驗數據有較好的擬合度。

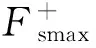
表4 動態參數辨識結果Table 4 Results of dynamic parameter identification

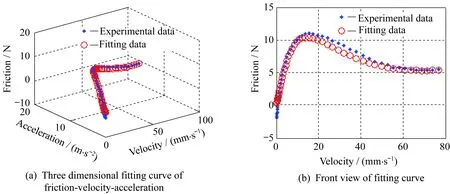
圖8 摩擦力-速度-加速度關系擬合曲線Fig.8 Fitting curve of friction-velocity and acceleretion

2.4Stribeck二元摩擦模型驗證

至此,Stribeck二元摩擦模型的全部參數已經辨識完畢。為了驗證此模型的有效性,分別對比了表2中第3組和第7組實驗工況下的摩擦力實驗值與模型預測值(見圖9、圖10)。

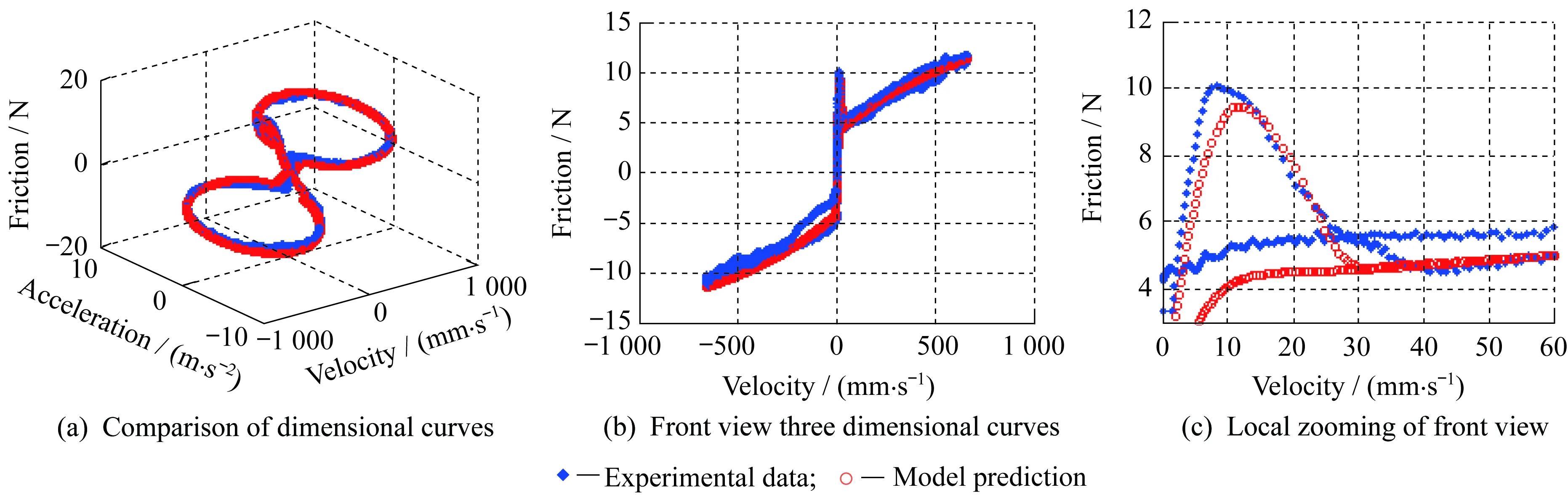
圖9 第3組摩擦實驗值與模型預測值對比Fig.9 Comparision between No.3 experimental data and model predictions

圖10 第7組摩擦實驗值與模型預測值對比Fig.10 Comparision between No.7 experimental data and model predictions

從圖9和圖10可以看出,Stribeck二元模型能夠很好地描述加速度增大造成Stribeck曲線后移和臨界摩擦力增大的現象以及高速下黏滯摩擦因子隨速度增加而逐漸下降的現象,與實驗結果較為符合。

3 結 論

(1) 通過不同工況下的摩擦實驗發現加速度對摩擦力有較大的影響:加速度越大,預滑動階段結尾處的臨界摩擦力也越大;加速度越大,混合潤滑區摩擦滯后現象越顯著,使得Stribeck曲線出現后移;加速時的摩擦現象與減速時存在差異。

(2) 通過不同勻速運動下的摩擦力曲線發現:在高速運動下,黏滯摩擦力并不隨速度呈線性變化,黏滯摩擦因子會隨著速度增加而逐漸下降。

(3) 針對這些摩擦特性,提出了考慮加速度影響的Stribeck二元摩擦模型。結合實驗數據辨識出了模型參數并通過對比其他工況下的實驗數據和模型預測值,驗證了Stribeck二元模型的有效性。

[1] 王偉進.直線電機的發展與應用概述[J].微電機,2004,37(1):45-46.

[2] CHEN J S,CHEN K C,LAI Z C,etal.Friction characterization and compensation of a linear-motor rolling-guide stage[J].International Journal of Machine Tools & Manufacture,2003,43(9):905-915.

[3] 張從鵬,劉強.直線電機定位平臺的摩擦建模與補償[J].北京航空航天大學學報,2008,34(1):47-50.

[4] 譚文斌,李醒飛,向紅標.修正黏性摩擦的LuGre模型的摩擦補償[J].天津大學學報(自然科學與工程技術版),2012,45(9):824-828.

[5] ZHANG Wei,ZHOU Yuan,MAO Junhong,etal.Some advances on investigating friction characteristics of rolling guide ways[J].Engineering Sciences,2013,11(1):83-88.

[6] CHENG Dejun,YANG Wansuk,PARK Jehong,etal.Friction experiment of linear motion roller guide THK SRG25[J].International Journal of Precision Engineering & Manufacturing,2014,15(3):545-551.

[7] XI Yinhu,ZHOU Yuan,ZHANG Wei,etal.An experimental method for measuring friction behaviors of linear rolling guides[J].Chinese Science Bulletin,2014,59(29/30):3912-3918.

[8] RAHMANI Mahdi,KRALL Stephan,BLEICHER Friedrich.Experimental investigations on stick-slip phenomenon and friction characteristics of linear guides[J].Procedia Engineering,2015,100:1023-1031.

[9] FERNANDO V,ROGELIO L H,MIGUEL P.Two-state GMS-based friction model for precise control applications[J].International Journal of Precision Engineering & Manufacturing,2016,17(5):553-564.

[10] 張新剛.基于擴展Stribeck效應的摩擦實驗建模及系統動力學研究[D].上海:上海交通大學,2009.

[11] STRIBECK R.Die wesentlichen eigenschaften der gleit und rollenlager:The key qualities of sliding and roller bearings[J].Zeitschrift des Vereines Deutscher Ingenieure,1902,46(38,39):1342-1348.

[12] TUSTIN A.Effects of backlash and of speed dependent friction on the stability of closed-cycle control systems[J].Journal Institution of Electrical Engineers,1947,94(1):143-151.

[13] BO L C,PAVELESCU D.The friction-speed relation and its influence on the critical velocity of stick-slip motion[J].Wear,1982,82(3):277-289.

[14] ARMSTRONG-HELOUVRY B.Control of Machines with Friction[M].USA:Kluwer Academic Publishers,1991.

FrictionCharacterizationandFrictionModelofALinear-MotorRolling-GuideStage

CHENHao,MENGJian,ANQi

(SchoolofMechanicalandPowerEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

In order to improve the motion precision of linear motor under the condition of high speed and large acceleration,research on friction characterization of linear-motor rolling-guide stage is required.The influences of acceleration and velocity on the friction were studied using the linear motor table.The break-away force at the end of pre-sliding regime increases with the increasing acceleration; friction lag during mixed lubrication regime is more significant with increasing acceleration,which makes the Stribeck curve appear backwards; Under the high speed movement,the viscous friction does not change proportionally with speed and viscous friction coefficient gradually decreases with increasing speed.According to these friction characteristics,Stribeck friction model including two variables considering the effects of acceleration is put forward.The model parameters is identified by using experimental data and by comparing the model predictions with experimental data under other experimental conditions,the effectiveness of the Stribeck friction model including two variables is verified.

linear-motor rolling-guide stage; friction characteristics; acceleration; friction model

1006-3080(2017)04-0571-07

10.14135/j.cnki.1006-3080.2017.04.018

2016-11-01

上海市設計學Ⅳ類高峰學科項目

陳 浩(1991-),男,江蘇鹽城人,碩士生,研究方向為工程摩擦學。

安 琦,E-mail:anqi@ecust.edu.cn

TH117.1

A