也談數學教學中如何培養創新能力

李麗偉

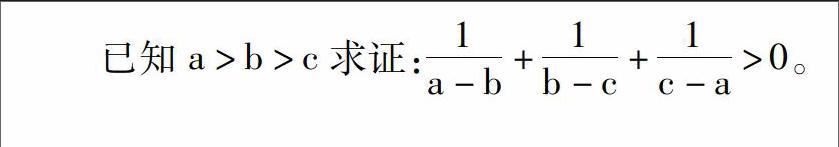
摘要：本文從如下幾個方面論述了如何加強學生創新能力的培養，重點論述了創設情景，形成培養創新精神的氛圍和重視求異思維、發散思維的培養是增強創新能力的重要渠道兩個方面。

關鍵詞：創新；問題；啟發

中圖分類號：G633.6 文獻標識碼：B 文章編號：1672-1578（2017）09-0175-02

創新是一個民族的靈魂，是一個國家興旺發達的不竭動力，沒有科學的創新，總是步人后塵，經濟就只能受制于人，更不能縮短差距。"因此，在數學教學中必須抓住對學生創新能力的培養。

目前教學現狀：雖然在教學模式、內容、方法等方面都作了有益探索，受應試教育的影響，課堂教學中解題數學占據了主導地位，通過大量的練習來學習數學，還是目前數學教學方法的主旋律，大量模仿性練習，對提高基本運算能力，邏輯推演能力以及學生解題能力的確行之有效。但卻使得數學教學缺乏創新精神，這說明加強對學生創新能力的培養任務還十分艱巨。

創新一般指，對思維主體來說是別出心裁，突破常規的，首次出現的思維活動，它包括發現新方法、揭示新規律、建立新理論、發明新技術、開發新產品、解決新問題等的思維活動。一個人要有不斷創新的精神也就離不開他的創造力。創造力是人通過一定的智力活動，在現有知識和經驗的基礎上，通過一定的重新組合和獨特加工，在頭腦中形成新產品的形象，并通過一定的行動使之成為新產品的能力。我們如何在數學教學中加強創新能力的培養呢？

1.重視知識發生的過程，培養創新意識

數學上每一個概念的引入都是由于產生實際需要或是研究某些問題的需要而產生的，一些重要定理的證明往往也體現了一些新的思路新的方法。也就是在當時研究某些問題的需要而有所創新方能突破。因此在教學中重視知識發生過程的教學就是讓學生不斷感受到隨著生產、生活實際的需要，科學研究等方面的需要是會不斷出現新問題，要解決這些問題就要求我們在不斷總結前人經驗的基礎上，用于探索，勇于創新。這無疑對于培養學生的創新意識是十分重要的。

2.創設情景，形成培養創新精神的氛圍

創新始于"問題"，愛因斯坦強調："發現問題和系統闡述問題肯定要比得到解答更為重要。解答可能僅僅是數學或實驗技能問題，而提出新問題、新的可能性，從新的角度去考慮老問題則要求創造性的想象，標志著科學的真正進步。"牛頓發現萬有引力始于他在蘋果樹下的思索："為什么蘋果從樹上掉下來，而不飛到天上去？"而"問題"來源于好奇心，強烈的好奇心會增強人們對外界信息的敏感性，對新出現的情況和新發生的變化及時作出反映，發現問題并追根溯源、激發思考，引起探索欲望，開始創新活動。許多看似偶然的發現其實都隱含著一種必然：發現者必然有強烈的好奇心理。愛因斯坦有一句名言："我并沒有什么特殊的才能，我只不過是喜歡尋根問底地追究問題罷了。"這段話一語道破了創新和發現的真諦：好奇心理、問題意識及鍥而不舍的探求。教學中使學生積極主動的投身于學習中是十分重要的，例：在"均值不等式"的教學中，可設計兩個實際應用問題，讓學生在探索中發現"均值不等式及推論"設計如下：①某商店在節前進行商品降價酬賓活動，擬分三個降價方案：甲方案是第一次打a折銷售，第二次打b折銷售，乙方案是第一次打b折銷售，第二次打a折銷售，丙方案是兩次都打a+b2折銷售，請問哪一種方案降價最多？②一個有毛病的天平（天平的兩臂之長略有差異，其它因素忽略）怎樣稱物體的重量？有人說只要有左右各稱一次，再相加除以二就可以了，你認為如何？學生通過審題、分析，展開小組討論，對于問題①，大多數學生能歸納為比較ab與（a+b2）2大小的問題，進而用特殊值猜出ab≤（a+b2）2（ 對于②有的同學也可結合物理知識，歸納為a+b與a+b2的大小，由①可得a+b2≥a+b。這樣的設計易產生明顯的意識傾向和情感共鳴。同時教育學生尊重科學，尊重知識，但又不迷信權威，敢于向權威挑戰的心理素質。

3.善于啟發引導，鼓勵創新熱情

心理學研究表明，榜樣的示范作用對創新意識的形成的重要性是不容忽視的，心理學家西蒙說"對榜樣的模仿，促進了創造性的智慧，從而對創造性產生有利的影響。"在班級集體里，一方面可以向學生介紹一些古今中外創新的例子。如：數學家高斯10歲時就發現了"1+2+3+....+100"這道題的特點，發現了快速計算的方法。典故"司馬光砸缸救人"的突破常規的思維方法。另一方面要注意發現班級集體中有創新精神的苗子。例如經常會有學生不完全按照老師規定的書寫格式、解題步驟以及解題方法去做。我們不要一概加以否定，仔細分析一下是否有某些合理性，是否有某些標新立異之處。如果發現了閃光點即時發揚鼓勵，不僅對受表揚的學生往往會終身難忘。同時對其他同學也起了導向作用，可以增強學生的創造欲，鼓勵學生的創新熱情。

4.突出數學思想方法是增強學生創新能力的基礎

學生創造能力的培養與基礎知識，基本技能的掌握是密不可分的。沒有扎實的基礎理論知識攀登科學高峰，即使有豐富的想象力，有一定的創造能力但缺乏基礎知識就會使他要想解決的問題不能圓滿解決，甚至半途夭折。因此在加強對學生創新能力培養的同時要處理好與基礎知識的關系。在基礎知識中對于一些死記硬背、模仿性習題應加以控制，不能對學生進行題海戰訓練，否則將影響學生的創新思維，而有關的重要數學思想方法應予以加強，這是學生終身受用的思維方法，只有把他掌握住了，學生才能在題海中暢游，對所學的內容運用自如，把所學知識轉化為能力，故數學思想方法是繼續發展，創造能力的基礎應當予以充分重視。

5.重視求異思維，發散思維的培養是增強創新能力的重要渠道

培養學生的觀察力和想象力。觀察力是人類智力結構的重要組成部分，敏銳的觀察力是創新活動的起步器。想象是客觀現實在人腦中的反映，豐富的想象力是創新活動的設計師。

因此，教學中應引導學生全方位，多角度的觀察問題，同時提供想象材料，誘發學生創造性的想象。例：教學中注意教學生一題多解，公式的正用逆用等等，在這過程中要注重求異思維能力和發散思維能力的培養。求異思維就是不墨守成規，尋求變異，伸展擴引，標新立異的一種思維傾向和思維活動。任何一位科學家的創造能力都可以看成是：創造能力=知識量求異思維能力。發散思維是多角度、多方位思考問題的一種思維活動，顯然沒有"求異"就不可能"發散"，要"發散"就必須"求異"，而當發散思維發生了質的飛躍時，就達到了求異思維的最高境界標新立異，即創新。因此發散思維和求異思維的培養是增強學生創新意識和創新能力的重要渠道。在教學中教師可有目的的設計一些開放題，讓學生對問題多角度分析，培養學生的發散思維能力，再進一步可讓學生刪改條件，探求結論等，都可以更好地培養學生的求異思維能力。重視開放題的研究，已知a>b>c求證：1a-b+1b-c+1c-a>0。

分析：有同學采用如下方法證明方法，1a-b+1c-a=c-b（a-b）（c-a）>0，因此原不等式成立，但發現似乎結論中的"1b-c"多余了，從這一點出發，引導學生觀察、分析、類似的有1a-b+1c-a=c-b（a-b）（c-a）>0，對此，師生可以共同努力將此題設計成開放題①已知a>b>c，且1a-b+1b-c+λc-a>0，求λ的范圍；②已知a>b>c，且λa-b+λb-c+1c-a≥0求λ的最小值。

6.轉變教育觀念是加強創新能力培養的可靠保證

我們已經站在新世紀的門檻之上，更新教育觀念，改變陳舊的教學觀，是21世紀教師的重任。只有這樣才能適應時代的需要。數學教育改革的重點之一就是如何培養學生的創新精神、創新能力，我們必須認識到：數學可以幫助人們更好的認識自然和人類社會，更好的適應日常生活，理解周圍世界；數學可以促進人們有條理的思考，有效的進行表達個交流，用數學分析問題和解決問題；同時通過數學實踐活動還可以發展學生的主動性，責任感和自信心，培養學生實事求是的態度和勇于探索的創新精神。事實上影響創新能力發展的因素是多方面的，而其中最為重要的是，教師要轉變教育觀念，增強教改意識，樹立新的教育觀，把提高素質作為教學的根本任務，才能營造創新環境，培養創新能力。

參考文獻：

[1] 李兆蘭 《素質教育創新》

[2] 李連方 《中學數學研究》endprint