分布式雷達對非合作目標彈道測量精度分析

宮志華,劉 洋,陳春江

(中國白城兵器試驗中心,吉林 白城 137001)

分布式雷達對非合作目標彈道測量精度分析

宮志華,劉 洋,陳春江

(中國白城兵器試驗中心,吉林 白城 137001)

針對非合作目標高精度彈道測量問題,提出采用一主三副脈沖體制分布式雷達系統組網測量模式,對系統提供的“多測距多測速”冗余測元采用基于函數約束的測元層數據融合計算方法,通過仿真計算,分析了彈道測量精度,結果表明:在合理布站條件下,如果雷達測元只含有隨機誤差,則彈道測量精度很高;如果測元存在系統誤差,則彈道測量精度有所下降。針對消除測元系統誤差,提出了4項修正內容。該文研究工作為今后作戰試驗條件下雷達組網測試和數據處理提供了參考。

分布式雷達;雷達組網;數據融合;信息處理;非線性函數;測量精度

Abstract:Aiming at the high-precision measurement problem for the trajectory of non-cooperative target,the network measuring model of the 1-master 3-deputies pulse-fashion distributed radar system was put forward.The measurement layer data-fusion based on function restriction was applied to the multi-range multi-velocity redundancy measurement elements supplied by this radar system.By simulation analysis,the ballistic measurement accuracy was analyzed.The results show that under the conditions of reasonable layout,the trajectory measurement accuracy is very high if the radar element contains only random errors.If the measured element contains system errors,the trajectory measurement precision declines.Four amendments to eliminate measurement system error were put forward.The research work provides reference for radar network test and data processing under the future combat training conditions.

Keywords:distributed radar;radar network;data fusion;information processing;non-linear function;measuring precision

隨著現代戰爭的發展,以電子干擾“軟”殺傷和反輻射導彈“硬”摧毀相結合的綜合電子戰能力的提高,特別是隱身目標、反輻射導彈、低空突防、綜合電子干擾和固定式布站所組成的“五大威脅”,對現代雷達尤其是傳統的單基地雷達系統構成嚴重威脅,而分布式雷達是對付以上威脅的重要手段,具有眾多優良的特性。分布式雷達可以增加系統的生存能力,提高目標狀態估計精度,增加目標狀態維數,增加對弱小目標的檢測概率。分布式雷達的機動性、靈活性和擴展性等技術優勢可以很好地滿足反導作戰的跟蹤與識別需求,美國已將分布式雷達技術作為美國下一代反導雷達的重要發展方向。

20世紀70年代后期到80年代初,我國開始了遠程導彈的高精度試驗和全程試驗,對彈道測量精度提出了更高的要求,并要求對整個主動段彈道進行高精度測量。為此,我國研制建設了多套高精度連續波測量系統[1],對主動段彈道進行聯合測量,該系統就是一種比較典型的特殊分布式雷達系統,在彈載(箭載)合作目標的配合下,采用“二發多收”測量形式,對導彈或火箭進行跟蹤測量,實現對彈道坐標、切向速度參數高精度評估,為導彈或衛星發射試驗任務的安全控制、實時引導、監控顯示,載人航天任務的逃逸救生以及導彈或火箭制導系統鑒定及改進設計等提供信息支持。但該雷達系統只能對合作目標進行跟蹤測量,已經不能滿足今后試驗與訓練相結合、試驗向實戰化轉變的新型試驗模式任務需求[2]。

基于上述情況,實戰化試驗的特點對雷達系統的戰場生存能力和目標狀態評估精度等提出了更大需求,使分布式雷達系統的建設和應用成為當前研究的一個熱點。本文提出一種一主三副脈沖體制的分布式雷達組網測量模式,對該雷達系統的工作模式、數據處理方法和測量精度進行了分析,為今后分布式雷達測量非合作目標提供了一種建設思路。

1 彈道參數估計模型

設計分布式彈道測量雷達系統,主要用于跟蹤測量非合作目標,如圖1所示,采用一主三副體制,主站雷達天線具有發射、接收功能,副站天線只具有接收功能。副站測量數據實時或事后匯于主站,由主站信息處理中心完成所有數據處理工作。

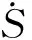
(1)

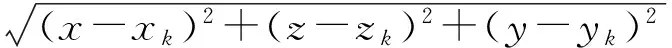
根據多源數據融合理論和靶場數據處理經驗,利用這些測元值可以進行測元層融合[3],獲得高精度彈道參數數據。測元層融合是指將各測量設備的測量數據集中起來,按一定準則直接融合得到最終的彈道,具有“集中式”的融合結構特點,能有效地融合測量信息,有利于提高估計的穩定性和精度,應用更科學、更廣泛。

對于較長彈道參數的數據融合處理,為了提高數據融合精度和降低數據處理過程的復雜度,考慮只采用雷達的距離和速度測元進行融合處理。雷達測角系統誤差的特性較復雜,不易用簡潔的數學模型加以表征,工程上也不易消除;而雷達距離測元系統誤差的特性簡單,并且工程上易于消除;雷達速度測元系統誤差非常小,可以忽略不計。綜合考慮多種因素,采用“多測距多測速”思想,對于跟蹤測量t時段的雷達測元數據,可以建立如下的彈道參數測量誤差方程:

(2)

式中:

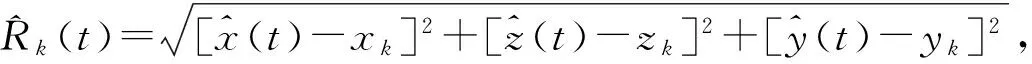
以下考慮如何實現對式(2)彈道待估參數的優化解算問題。依據測量冗余度ρ的概念,即測量量(樣本)數量m與待估狀態量數量n之間的比值:ρ=m/n,系統測量冗余度越高,對狀態量估計采用一定的估計方法抵御不良數據和消除誤差的影響就越好,冗余測量的存在是狀態量估計提高數據精度的基礎。因此,為提高測量冗余度,需要最大限度壓縮彈道參數數量,即待估狀態數量,通常采用函數約束的誤差模型最佳彈道估計(error model best estimate of trajectory,EMBET)事后數據融合方法[3-4],其核心思想是采用某種數學函數對彈道參數進行表征,構成非線性有限元聯合模型。目前,可以有效擬合逼近遠射程非平穩彈道參數的函數有樣條函數和Hermite函數等[5-6],這些函數的共同特點是通過對彈道時間節點的合理控制實現較長彈道不同段與段之間一定階數的平滑連接,進而對較長彈道數據中的低頻和次低頻信號實現精確逼近,截斷誤差可以忽略不計[3]。彈道參數表征如下:

(3)

式中:b=(bxbybz),為表征函數系數;T=(txtytz),為彈道時間節點分布。

ε=Y-F(C,T)

(4)

式中:Y為各測元的各時刻測量數據形成的列向量,待估參數記為C=bT,ε為各測元的各時刻測量數據隨機誤差形成的列向量。

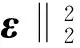
(5)

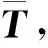
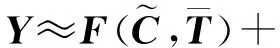
(6)

式中:記V=為多元函數關于C的梯度矩陣在處的值。

易知,依據最小二乘估計,式(6)的解為

(7)

2 仿真實例分析

基于上述分布式雷達系統設計思想和數據融合處理方法,仿真驗證彈道測量精度。首先仿真計算出一條理論彈道,彈道坐標和速度與相對時間曲線如圖2所示。

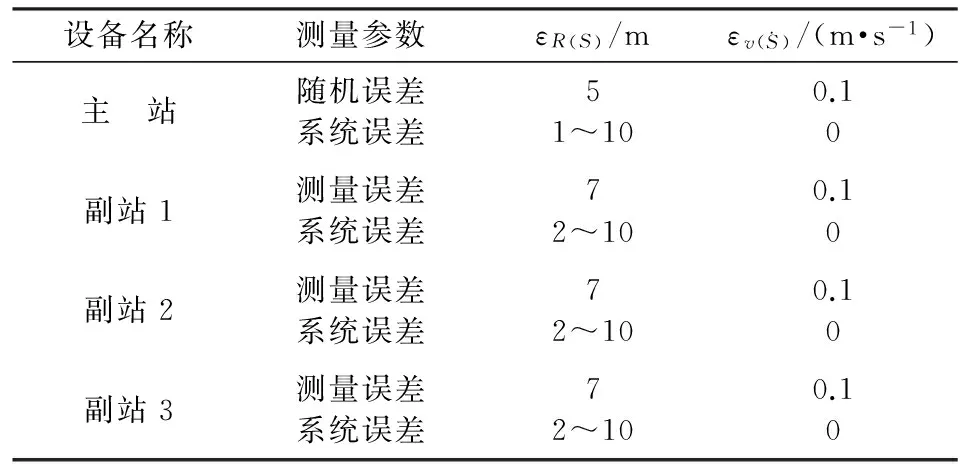
表1 分布式雷達各站測元誤差分配表

設定3種雷達布站方案,總體按照星型布站模式,每種方案的主站均布設在發射陣地附近,副站按照站與站之間基線分別為50 km,100 km和150 km布設。在考慮較好的幾何關系的基礎上,3種布站方案分別覆蓋彈道射程為70 km,130 km和200 km左右,因此,每種方案分析計算彈道長度也以此為依據。例如,基線為150 km方案中,雷達布站與彈道幾何關系如圖3所示。

如果不考慮系統誤差的影響,則3種布站方案的彈道計算誤差曲線如圖4～圖6所示,圖中,e,ev分別為坐標和速度誤差。誤差統計結果如表2～表4所示,表中,μ,σ,E分別為坐標參數的平均值、均方差和總誤差;μv,σv,Ev分別為速度參數的平均值,均方差和總誤差。

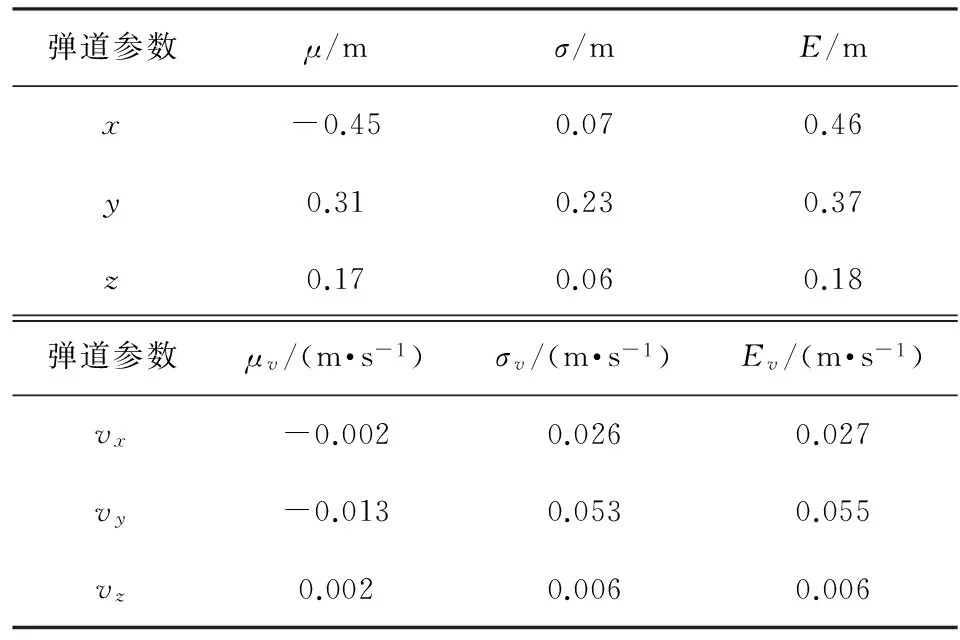
彈道參數μ/mσ/mE/mx-0.450.070.46y0.310.230.37z0.170.060.18彈道參數μv/(m·s-1)σv/(m·s-1)Ev/(m·s-1)vx-0.0020.0260.027vy-0.0130.0530.055vz0.0020.0060.006

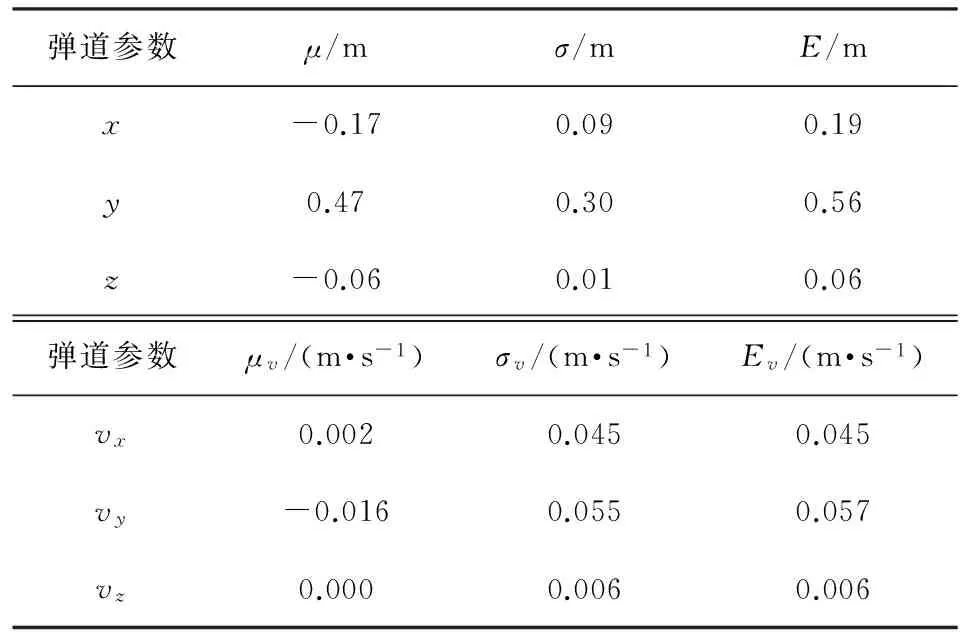
表3 基線100 km彈道誤差統計值(無系統誤差)

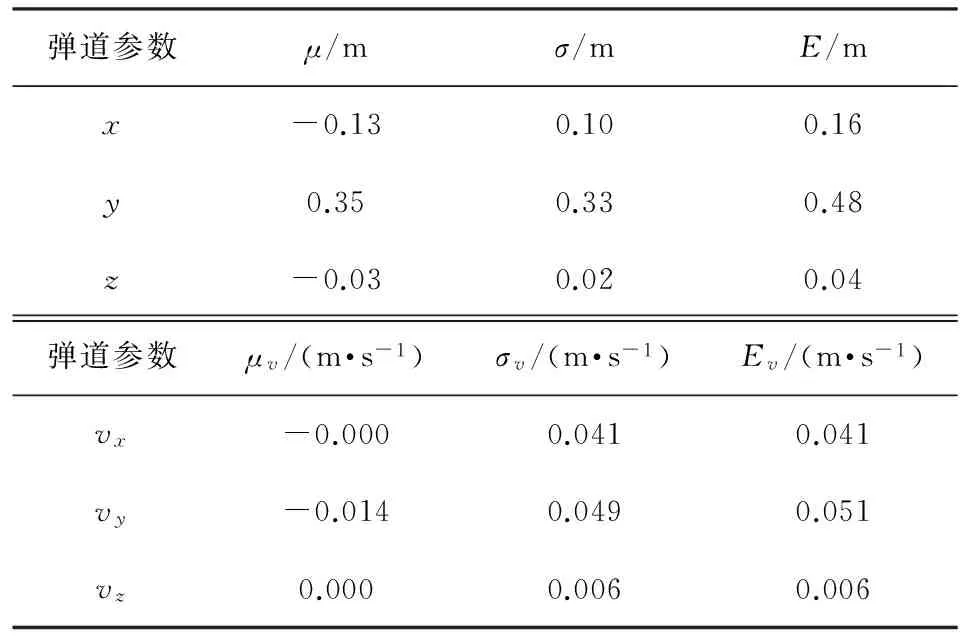
表4 基線150 km彈道誤差統計值(無系統誤差)

從上述誤差統計分析結果可見,在雷達各測元只含有隨機誤差的情況下,針對此仿真彈道,在初始彈道段,由于彈道高度相對于各雷達站仰角較低,沒有構成較好的幾何關系,因此,彈道誤差相對大一些,但整體彈道計算精度還是非常高,坐標定位精度可以達到1 m左右,切向速度精度可以達到0.1 m/s左右。

如果考慮測元系統誤差的影響,則3種布站方案的彈道計算誤差曲線如圖7～圖9所示,誤差統計結果如表5～表7所示。

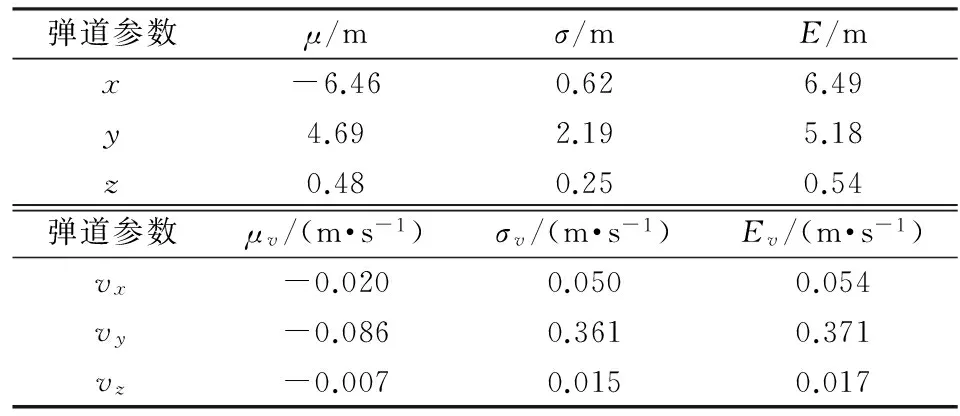
彈道參數μ/mσ/mE/mx-6.460.626.49y4.692.195.18z0.480.250.54彈道參數μv/(m·s-1)σv/(m·s-1)Ev/(m·s-1)vx-0.0200.0500.054vy-0.0860.3610.371vz-0.0070.0150.017

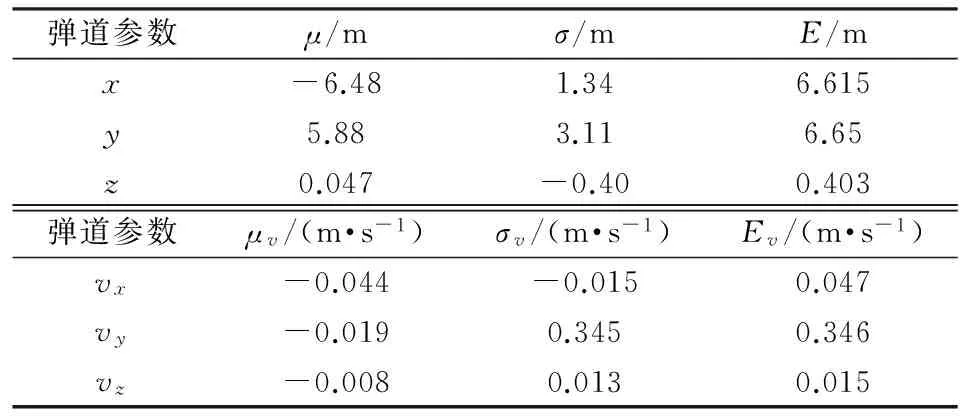
表6 基線100 km彈道誤差統計值(有系統誤差)

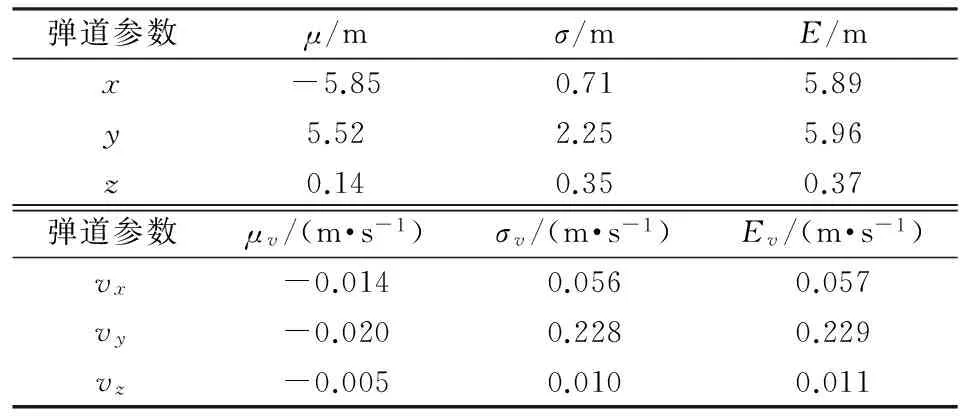
表7 基線150 km彈道誤差統計值(有系統誤差)

從上述誤差分析結果可見,在雷達測元含有系統誤差的情況下,在測元種類、測元數量、布站條件和計算方法等各種因素完全相同的條件下,坐標定位精度下降到10 m左右,切向速度精度下降到0.5 m/s左右。可見,參與融合計算的雷達各測元系統誤差對最終彈道參數的解算影響很大,對距離測元的影響尤重。

3 結束語

從分布式雷達系統設計建設和靶場應用角度考慮,本文設想采用一主三副的脈沖分布式雷達組網模式對非合作目標進行彈道測量,并著重探討了該系統對彈道參數測量精度的能力問題。從仿真計算結果來看,采用“多測距多測速”測元進行彈道融合計算,在雷達布站比較合理的前提下,如果不考慮測元系統誤差的影響,彈道參數計算精度是非常高的;考慮測元系統誤差后,彈道參數計算精度大幅下降。

因此,為滿足實際工程測量需求,實現分布式雷達對非合作目標的彈道高精度測量,除盡量減小雷達系統原始測元的隨機誤差以外,關鍵問題應是如何最大限度消除雷達測元的系統誤差。為此,后續應考慮在4個方面開展重點研究:①高精度電波折射修正研究;②目標跟蹤部位不一致修正研究;③雷達布站優化幾何關系研究;④雷達高精度標校研究。如果這些問題能夠得到很好的解決,則采用分布式雷達系統對非合作目標的彈道測量是非常精確和可靠的。

[1] 李雪光.靶場高精度測速雷達系統[M].北京:國防工業出版社,2014. LI Xue-guang.High precision measuring velocity radar system in base[M].Beijing:National Defensen Industry Press,2014.(in Chinese)

[2] 李雪光.連續波反射式雷達方案設計與實現[J].導彈試驗技術,2016,117(1):30-33. LI Xue-guang.The project design and realization for continuous wave reflect radar[J].Missile Test Technology,2016,117(1):30-33.(in Chinese)

[3] 郭軍海.彈道測量數據融合技術[M].北京:國防工業出版社,2012. GUO Jun-hai.Trajectory data fusion technology[M].Beijing:National Defensen Industry Press,2012.(in Chinese)

[4] 王正明,易東云,周海銀.彈道跟蹤數據的校準與評估[M].長沙:國防科技大學出版社,1999. WANG Zheng-ming,YI Dong-yun,ZHOU Hai-yin.Tracking trajectory data calibrating and evaluating[M].Changsha:National University of Defense Technology Press,1999.(in Chinese)

[5] 宮志華,周海銀,郭文勝,等.基于樣條函數表征目標運動軌跡事后數據融合方法研究[J].兵工學報,2014,35(1):120-127. GONG Zhi-hua,ZHOU Hai-yin,GUO Wen-sheng,et al.Data fusion algorithm for target trajectory determination based on spline function representation[J].Acta Armamentarii,2014,35(1):120-127.(in Chinese)

[6] 宮志華,段鵬偉,岳銳,等.外彈道多源異類測元數據融合仿真分析[J].彈道學報,2014,26(4):19-23. GONG Zhi-hua,DUAN Peng-wei,YUE Rui,et al.Simulation analysis of data fusion with multi-source heterogeneous measurement elements[J].Journal of Ballistics,2014,26(4):19-23.(in Chinese)

[7] 崔書華,許愛華,趙樹強,等.高精度跟蹤測量系統測元數據融合處理方法[J].彈箭與制導學報,2013,33(3):167-170. CUI Shu-hua,XU Ai-hua,ZHAO Shu-qiang,et al.Fusion processing method of measurement elements in high-precision tracking measuring system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(3):167-170.(in Chinese)

[8] 周海銀.空際目標跟蹤數據的融合理論和模型研究及應用[D].長沙:國防科學技術大學,2004. ZHOU Hai-yin.Researches on theories and models of spatial targets tracking data fusion with applications[D].Changsha:Nation University of Defense Technology,2004.(in Chinese)

AnalysisonPrecisionofDistributedRadarMeasuringNon-cooperativeTargetTrajectory

GONG Zhi-hua,LIU Yang,CHEN Chun-jiang

(Baicheng Ordnance Test Center of China,Baicheng 137001,China)

2017-05-19

宮志華(1975- ),男,高級工程師,研究方向為外彈道數據融合技術及應用。E-mail:gzh63298@126.com。

V557

A

1004-499X(2017)03-0043-06