大質量鎢破片沖擊多層間隙蓋板炸藥數值模擬與試驗研究

梁 斌,馮高鵬,周婕群,魏雪婷,朱永清

(中國工程物理研究院 總體工程研究所,四川 綿陽 621900)

大質量鎢破片沖擊多層間隙蓋板炸藥數值模擬與試驗研究

梁 斌,馮高鵬,周婕群,魏雪婷,朱永清

(中國工程物理研究院 總體工程研究所,四川 綿陽 621900)

為分析大質量破片對多層蓋板炸藥沖擊起爆閾值的影響因素,采用SPH和FEM相結合的方法開展了不同蓋板厚度和不同蓋板間隔情況對起爆閾值影響的數值模擬。在此基礎上,采用二級輕氣炮作為加載手段,進行了大質量鎢合金破片沖擊不同蓋板及間隙情況下炸藥沖擊起爆試驗研究,獲得了起爆閾值。數值模擬與試驗結果相一致,表明采用SPH與FEM相結合的方法可以較好地模擬此類問題。通過擬合得到了大質量破片沖擊起爆閾值速度與沖擊角度之間的經驗關系式。分析結果表明,大質量破片沖擊產生的大量二次破片對起爆閾值速度和起爆延遲時間具有較大的影響。

爆炸力學;沖擊起爆;數值模擬;光滑粒子法;起爆閾值

Abstract:In order to investigate the influence factor of large-mass fragments on shock initiation,the smoothed particle hydrodynamics(SPH)and finite element method(FEM)was combined,and the influence of different thinckness and different spacing of cover plates on initiation threshold was numerically simulated.The two-stage gas gun was applied,and the experiment of large-mass tungsten fragments impacting explosive was carried out.The critical initiation velocity was obtained.The simulation results are consistent with experimental results,and the SPH/FEM coupling method can be applied to analyze the velocity shock initiation problem.The correlations between critical initiation velocity and oblique impact angle were obtained by data fitting.Results show that the secondary fragments deriving from tungsten fragments have an important effect on the initiation velocity and the initiation delay-time.

Keywords:mechanics of explosion;shock initiation;numerical simulation;smoothed particle hydrodynamics;critical initiation velocity

裝藥沖擊安全性、反導戰斗部設計以及炸藥存儲安全性等工程問題中,裝藥的沖擊起爆特性備受關注。反導戰斗部通常采用裝藥爆炸產生的高速預制/半預制小質量破片(幾克至十幾克)引爆來襲導彈裝藥,實現對導彈的有效攔截。但隨著制導彈藥防護性能的增強,傳統的反導彈藥產生的小質量破片難以引爆來襲導彈,其反導性能受到嚴峻挑戰。據此,國外研制了新型的大質量重金屬破片戰斗部,如愛國者-3(PAC-3)動能欄截彈,其采用24枚200余克的破片作為毀傷元[1],成功攔截“飛毛腿”等戰術導彈。

對大多數戰術導彈戰斗部裝藥結構,可將此問題簡化為破片對具有一定厚度和間隙的多層蓋板裝藥的沖擊起爆問題,涉及破片穿甲過程,殼體與炸藥在高溫、高壓、高應變率下非定常的多相復雜反應過程[2-6],從理論上研究該問題存在較大的難度和挑戰性。目前研究者廣泛采用數值模擬并由少量試驗對其進行驗證的方法進行研究。當前,國內外學者對小質量破片沖擊單層無間隙蓋板炸藥這類問題進行了大量研究[7-10],但是由于高速加載以及防護等困難,對于超過100 g的大質量破片沖擊起爆研究較少[11],對于大質量破片沖擊帶間隙的多層蓋板炸藥起爆問題方面的研究鮮見公開報道。鑒于此,本文采用SPH(smoothed particle hydrodynamics)和FEM(finite element method)相結合的數值建模方法,運用“升-降”法對大質量鎢破片沖擊多層間隙蓋板炸藥起爆性能進行了模擬。在此基礎上,采用二級輕氣炮作為加載手段,開展了大質量鎢破片沖擊不同間隙蓋板炸藥起爆試驗,驗證了數值模擬結果;獲得了影響大質量破片沖擊多層間隔蓋板炸藥起爆閾值的主要因素。

1 數值建模方法與材料模型驗證

對于破片沖擊起爆問題,當前廣泛采用的是Lee和Tarver[4-5]在Cochran方程的基礎上提出的反應速率方程及點火—燃燒—快反應三項形式的反應速率方程[6-7],其計算結果與其PoP(progresses of a propagating)和壓力歷程曲線都符合較好,因此本文采用該模型研究沖擊起爆過程。高速沖擊過程中,破片和靶板將出現較大變形和破壞,單獨采用Lagrange、ALE(arbitrary langrange eluer)方法均難以重現整個物理過程,為此,本文采用有限元與光滑粒子相結合的方法對該問題進行建模與分析。

1.1 數值建模

本文主要基于文獻[9]試驗,并參考文獻[10-12]中數值模擬材料模型及參數,建立破片沖擊帶蓋板炸藥的沖擊起爆模型,通過數值模擬與試驗結果比對,驗證數值模型。依據試驗,建立不同直徑鎢珠沖擊3.65 mm厚的鉭蓋板及與之接觸50 mm厚的B炸藥。

建模中,鎢珠采用SPH粒子,粒子直徑為0.5 mm。蓋板、炸藥采用Lagrange網格。根據炸藥爆轟波寬度,網格劃分尺寸控制在0.5 mm以內。鎢珠與蓋板、炸藥以及蓋板與炸藥之間采用接觸算法,根據對稱性,建立四分之一模型,在炸藥不同位置設置測量點,如圖1所示。

1.2 材料模型及其主要參數

炸藥的沖擊響應采用Lee-Tarver三項式點火增長模型模擬[4,13],該方程可很好地模擬非均勻炸藥的沖擊起爆特性:

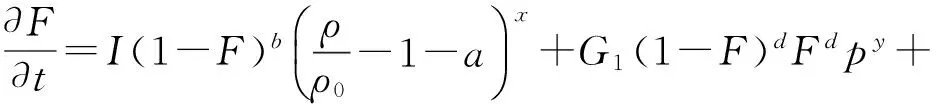
(1)

式中:F是反應率,即反應炸藥與未反應炸藥之比;a,b,c,d,G1,G2,I,u,s,w,e,f為炸藥參數。

采用JWL狀態方程描述炸藥的反應物和未反應物,該方程描述了壓力與相對體積V、單位體積以及初始能量E的關系:

(2)

式中:ω,R1,R2,A,B為炸藥常數;E為CJ爆轟釋放的內能。

本文采用高能B炸藥,主要參數如表1、表2[10,13-14]所示。

表1 B炸藥Lee-Tarver模型參數

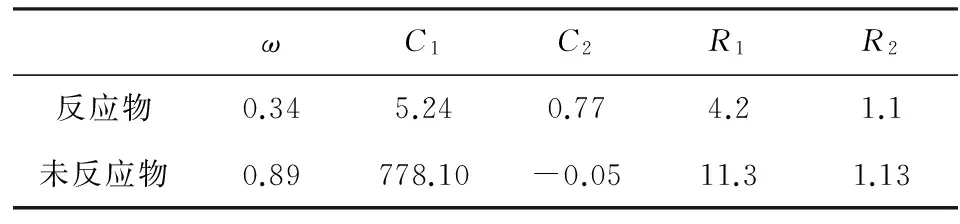
表2 B炸藥JWL狀態方程參數

應用Johnson-Cook強度模型和Gruneison狀態方程[14-15]描述鎢和坦材料。其主要參數取自AUTODYN材料庫[13]。

1.3 數值模擬模型驗證

為模擬不同直徑D鎢珠對蓋板炸藥的沖擊起爆閾值,采用了“升降法”。鎢破片沖擊起爆過程中炸藥壓力與反應率云紋如圖2、圖3所示,從圖中可以看出,破片高速沖擊情況下,在幾μs時炸藥局部反應率就達到1,大約10 μs時,炸藥峰值壓力就上升到29 GPa,隨后剩余炸藥很快反應。單個破片沖擊帶蓋板B炸藥的起爆壓力閾值約為7 GPa,與文獻[2]中給出的起爆閾值一致。

單個和多個鎢球沖擊接觸蓋板炸藥的影響因素及炸藥反應過程,具體見文獻[10,15]。

表3給出了不同直徑鎢珠沖擊蓋板炸藥起爆閾值。數值模擬計算得到的起爆閾值和文獻中沖擊起爆試驗結果一致,驗證了本文數值建模方法及模型參數的合理性。

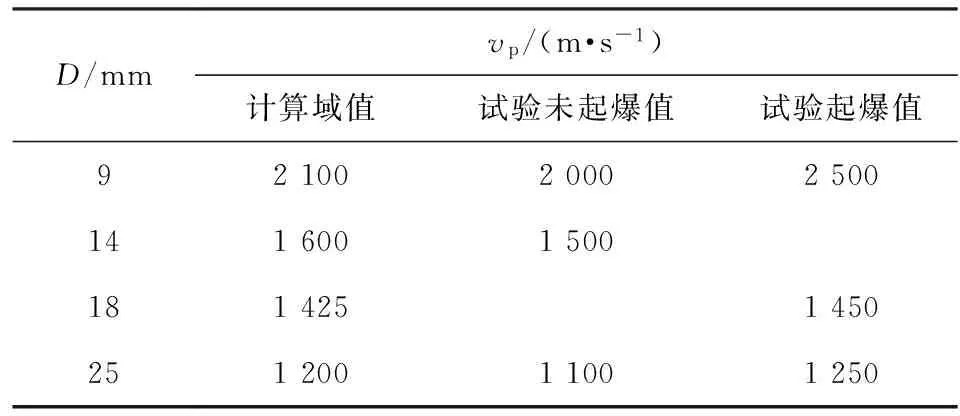
表3 不同直徑鎢珠沖擊蓋板炸藥起爆閾值對比

2 大質量鎢破片沖擊蓋板炸藥數值建模與分析

2.1 SPH與FEM相結合方法沖擊起爆數值建模

破片與蓋板在高速沖擊情況下存在較大的變形和破壞,其網格存在畸變,導致計算精度降低和計算時間步長變小。為此,破片和玻璃鋼、鋁板和鋼板采用SPH粒子,炸藥采用Lagrange單元,SPH粒子直徑和炸藥單元尺寸均為0.5 mm。破片與靶體以及靶體之間采用接觸算法,為減小邊界的影響,炸藥側面和下表面采用無反射邊界條件。

對2種破片、4種靶體進行建模,如表4、表5所示。表中,m1,l1,b1,h2分別為破片的質量、長、寬和高。由于破片著角θ超過80°后出現跳飛,因此著角θ計算范圍取值從0°到80°,間隔5°。

表4 破片結構參數

表5 靶體結構參數

圖4給出了鎢破片1(記為F1)和鎢破片2(記為F2)以著角θ=70°沖擊靶體4(記為T4)的數值計算模型,為了測取炸藥在沖擊過程中的響應,在炸藥中設置了不同測取點,記為G1,…,G7。

2.2 多層間隔蓋板炸藥沖擊起爆數值模擬結果

采用升降法對不同情況沖擊過程進行了數值模擬,根據起爆結果調整破片著靶速度,其調整速度最小間隔為25 m/s,直至獲得起爆和未起爆的速度值。圖5、圖6分別給出了破片F1以60°著角沖擊不同蓋板炸藥壓力與炸藥反應率云圖。由圖可見,破片F1以1 475 m/s速度沖擊無間隙蓋板炸藥,在50 μs時刻炸藥起爆,而破片1以同樣角度沖擊3層間隔蓋板炸藥,需要2 025 m/s的速度才能起爆,從炸藥中監測點可看出,其起爆所需時間約為70 μs,起爆時間較沖擊無間隙蓋板炸藥靶體情況長。

圖7、圖8給出了破片F1以3 250 m/s速度、80°著角沖擊靶板T4的過程及監測點壓力曲線,從圖7中可看出,高速沖擊過程中靶板破碎產生大量的二次破片,并與沖擊方向呈一定角度向四周飛散,其中一部分破片沖擊下層蓋板。盡管鎢破片在100.0 μs時已從第一層靶面跳飛,但大量二次破片對下層蓋板炸藥持續沖擊,致使炸藥在約110 μs時刻被引爆,見圖8。

圖9給出了鎢破片對不同蓋板炸藥沖擊起爆的著角與速度閾值。從圖中可看出,破片著角小于30°時,著角對起爆閾值影響較小,當著角超過60°時,起爆閾值隨著角增加迅速增大,當著角超過70°時,起爆閾值的增加尤為突出,主要是因為此時破片出現跳飛,起爆主要靠二次破片的累積和持續的沖擊效應引爆炸藥。

靶板間隙對引爆閾值也有較大的影響,對于本文中計算條件,多層間隙蓋板炸藥的沖擊起爆閾值較蓋板炸藥接觸情況起爆閾值高20%～40%,其差距隨著角的增加而增大。在有間隙情況下,鎢破片開始階段沖擊上層靶板產生的沖擊波難以直接傳入炸藥中,只有在破片穿透復合材料與鋁靶后沖擊與炸藥接觸的蓋板產生的沖擊波才能對炸藥起爆產生直接作用。如果破片著角大于臨界跳飛角,則鎢破片將不能直接沖擊與炸藥接觸的蓋板,此時炸藥的起爆僅靠二次破片沖擊作用[11],因此,此時起爆閾值與無間隙情況差距進一步增大。

3 大質量破片沖擊多層間隔蓋板炸藥試驗

3.1 試驗布局

為驗證上述計算結果以及分析彈靶交匯條件對起爆閾值的影響,設計了不同角度鎢破片沖擊間隔蓋板炸藥試驗。破片及試驗布局如圖10所示。破片通過二級輕氣炮發射并加速到預定的速度。蓋板炸藥試驗件、見證板及壓力傳感器均通過安裝板安裝在密閉防爆容器中。壓力傳感器安裝在見證板前端,測量破片沖擊后爆炸容器中的壓力。

3.2 試驗狀態判定

破片沖擊蓋板炸藥可能出現未反應、燃燒、局部爆轟、完全爆轟等狀態。判斷依據如下:

①未反應。壓力信號與典型應力波振蕩衰減波形相似,試驗后蓋板變形不明顯,靶室有大量殘余顆粒狀炸藥。

②爆燃。壓力信號無爆轟特征波形,試驗后蓋板向前變形不明顯,側板有明顯燃燒痕跡,且側板與上掛板之間間隙有較多粉末狀殘余炸藥。

③局部爆轟。壓力波形在破片撞擊蓋板后緊隨出現峰值,試驗后蓋板向前、側板向外變形較明顯,側板與頂板之間的間隙、側板上方有較多蠟狀殘余炸藥以及明顯的燃燒痕跡。

④完全爆轟。壓力波形和典型的爆轟波波形相似,試驗后蓋板炸藥部分形成比炸藥直徑稍大的圓形破孔,側板向外嚴重變形,頂板及其支撐結構變形隆起,靶室內壁、頂板、側板上方無殘余炸藥。

具體判定過程中,壓力波形作為首要判斷依據,然后根據試驗后蓋板、側板等情況綜合分析進行判定。

3.3 試驗引爆閾值確定方法

破片撞擊蓋板炸藥的反應十分復雜,由于諸如碰撞壓力,環境溫度、濕度,炸藥與蓋板結合緊密情況等多種因素的作用,使其爆炸程度在引爆閾值速度附近與撞擊速度并不是嚴格的單調線性關系。

引爆閾值速度計算原則:某一碰撞角下引爆閾值速度取局部爆炸狀態的最低速度與未爆狀態最高速度的平均值。若某碰撞角度下無未爆狀態,則閾值取爆燃與局部爆炸相近速度的平均值。若某碰撞角度下既無未爆狀態又無局部爆炸狀態,則其閾值取最高爆燃狀態速度。

3.4 沖擊起爆試驗結果與分析

試驗獲得16發有效數據。不同狀態下測試獲得的典型壓力歷程曲線如圖11所示。圖中,YB-14-ch4表示第14發試驗中第4個傳感器所測數據,其余依次類推。破片以70°著角沖擊間隙蓋板炸藥試驗后見證板破壞以及蓋板炸藥如圖12和圖13所示。

70°碰撞角狀態共進行6次試驗,數據采集成功5次,具體如表6所示。其中YB-14和YB-15試驗壓力信號于2 000 μs附近與典型應力波振蕩衰減波形相似(圖11(a)),試驗后蓋板向前變形不明顯,靶室內有殘余顆粒狀炸藥(圖12),狀態判斷為未爆。YB-10試驗壓力波形在2 000 μs附近出現峰值(圖11(c)),試驗后蓋板向前、側板向外變形較明顯,側板與頂板之間的間隙、側板上方有較多蠟狀殘余炸藥以及明顯燃燒痕跡(圖13),狀態判為局部爆炸。該狀態下引爆閾值速度按上述計算方法,取YB-10,YB-14發射速度平均值為2 360 m/s,綜合上述分析認為該值為70°著角沖擊情況下的起爆閾值。

分析試驗結果,著角θ分別為30°,60°,70°,80°下引爆閾值分別為1 716 m/s,2 085 m/s,2 420 m/s,3 150 m/s。對試驗引爆閾值進行指數方程擬合,獲得引爆閾值經驗曲線如圖14(a)。圖14(b)給出了數值模擬與試驗引爆閾值的對比,并對數值模擬閾值進行指數方程擬合,其中,擬合方程為y=A1exp(x/t1)+y0,R2=0.996,y0=1.510±0.034,A1=0.036±0.011,t1=21.199±1.704。

表6 破片以70°著角沖擊時試驗狀態

從圖14可知,破片沖擊引爆閾值vp隨沖擊角度增大呈指數增大,當沖擊角度超過70°后,引爆閾值急劇增加,這主要是由于超過一定角度后,破片沖擊出現跳飛情況,主要依靠沖擊產生的二次破片來引爆炸藥,其趨勢與前述數值模擬結果一致。從圖14(b)可看出,數值模擬獲得的起爆閾值與試驗獲得的起爆閾值吻合較好,說明本文采用的數值建模與分析方法具有一定的合理性,可用于此類問題的模擬分析。

4 結束語

采用SPH與FEM相結合的方法建立了破片沖擊多層間隔蓋板炸藥數值模型,開展了破片在不同沖擊角度下的沖擊引爆試驗研究,獲得以下初步結論:

①數值模擬獲得的引爆閾值與試驗結果一致,說明采用SPH與FEM相結合的方法可有效模擬大質量破片對多層間隔蓋板炸藥沖擊起爆問題;

②大質量破片對多層間隔蓋板炸藥沖擊產生的二次破片對起爆閾值具有重要影響,其起爆時間相對較長,二次破片與大質量破片共同引起炸藥的反應;

③大質量破片對多層間隙蓋板炸藥的引爆閾值隨破片沖擊角度的增加呈指數增長。當著角超過70°時,引爆閾值急劇增大,著角大于80°時,因破片出現跳飛,炸藥難以引爆。

由于影響大質量破片對多層間隙蓋板炸藥沖擊起爆閾值的因素較多,如炸藥配方、裝填工藝、內部缺陷等,同時還受某些隨機因素的影響,很難對某類炸藥給出明確的起爆閾值,工程中往往給出特定條件下的起爆概率,其起爆機理及影響因素還需開展大量的研究工作。

致謝中國工程物理研究院化工材料研究所對試驗裝藥、空氣動力研究中心第四研究所對試驗實施給予了大力支持,在此表示感謝。

[1] 孫亞力.不斷改進的“愛國者”地空導彈系統[J].現代軍事,2000,30(2):27-29. SUN Ya-li.Improvement of “PAC” air-to-ground missile system[J].Modern Armament,2000,30(2):27-29.(in Chinese)

[2] CHEN Wei-dong,ZHANG Zhong,LIU Jia-liang.Numerical simulation and analysis of shock initation of shielded explosive impacted by fragments[J].Acta Armamentii,2009,30(9):1 187-1 191.

[3] 張寶平,張慶明,黃風雷.爆轟物理學[M].北京:兵器工業出版社,2001:340-344. ZHANG Bao-ping,ZHANG Qing-ming,HUANG Feng-lei.Detonation physics[M].Beijing:Ordnance Industry Press,2001:340-344.(in Chinese)

[4] HELD M.Initiation phenomena of uncovered or covered high explosive charges by jets or projectile[C]//Proceedings of the 3rd International Autumn Seminar on Propellants,Explosive,and Pyrotechnics.Chengdu:Sichuan Publishing House of Science & Technology,1999:273-289.

[5] LEE E L,TARVER C M.Phenomenological model of shock initiation in heterogeneous explosives[J].Journal of Phys,Fluids,1980,23(12):2 362-2 372.

[6] CHEN J K,CHING H K,ALLAHDADI F A.Shock-induced detonation of high explosives by high velocity impact[J].Journal of Mechanics of Materials and Structures,2007,2(9):1 701-1 721.

[7] URTIEW P A,VANDER K S,TARVER C M,et al.Shock initiation experiments and modeling of composition B and C-4[C]//Proceedings of the 13th International Detonation Symposium.Norfolk,VA:Office of Naval Research,2006:55-61.

[8] 王樹山,李朝君,馬曉飛,等.鎢合金破片對屏蔽裝藥撞擊起爆的實驗研究[J].兵工學報,2001,22(2):189-191. WANG Shu-shan,LI Chao-jun,MA Xiao-fei,et al.An experimental study on the initiation of covered charge impacted by tungsten alloy fragments[J].Acta Armamentii,2001,22(2):189-191.(in Chinese)

[9] MURPHY M J,LEE E L.Modeling shock initiation in composition B[C]//The 10th International Detonation Symposium.Los Alamos,NM:Los Alamos National Laboratory,1993:73-84.

[10] 梁斌,馮高鵬,魏雪婷.多枚破片沖擊引爆帶蓋板炸藥數值模擬分析[J].彈箭與制導學報,2013,33(6):43-47. LIANG Bin,FENG Gao-peng,WEI Xue-ting.Numerical simulation on shock initiation of composition explosive of cover board subjected to multi-fragment[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(6):43-47.(in Chinese)

[11] 趙海軍,盧永剛,梁斌.多層蓋板炸藥在鎢破片撞擊下起爆數值模擬研究[J].四川兵工學報,2015(5):75-78. ZHAO Hai-jun,LU Yong-gang,LIANG Bin.Study on numerical simulation of multilayer plate explosive detonated by tungsten fragment impact[J].Journal of Sichuan Ordnance,2015(5):75-78.(in Chinese)

[12] LAWRENCE W,STARKENBERG J,KRZEWINSKI B.Secondary effects on projectile impact shock initiation[C]//Proceedings of the 13th International Detonation Symposium.Norfolk,VA:Office of Naval Research,2006:839-846.

[13] 崔凱華,洪滔,曹結東.射彈沖擊帶蓋板Comp B裝藥起爆過程數值模擬[J].含能材料,2010,18(3):286-289. CUI Kai-hua,HONG Tao,CAO Jie-dong.Numerical simulation of shock initiation in covered composition B by projectile impact[J].Chinese Journal of Energetic Materials,2010,18(3):286-289.(in Chinese)

[14] Century Dynamics Corporation.AUTODYN users manual[M].California:Century Dynamics Corporation,2005:234-249.

[15] 鄭平剛,趙鋒,張振宇.圓頭鋼彈對PBX-9404炸藥撞擊起爆的數值模擬[J].高壓物理學報,2002,16(1):29-34. ZHENG Ping-gang,ZHAO Feng,ZHANG Zhen-yu.Numerical simulation of initiation of PBX-9404 impacted by round-nosed steel projectiles[J].Chinese Journal of High Pressure Physics,2002,16(1):29-34.(in Chinese)

NumericalSimulationandExperimentalStudyontheExplosiveWithMulti-layerIntervalTargetsImpactedbyLarge-massTungstenFragments

LIANG Bin,FENG Gao-peng,ZHOU Jie-qun,WEI Xue-ting,ZHU Yong-qing

(Institute of Systems of Engineering,China Academy of Engineering Physics,Mianyang 621900,China)

2016-12-10

國家自然科學基金項目(11672278)

梁斌(1976- ),男,高級工程師,博士,研究方向為常規武器研制及毀傷評估。E-mail:lb_110119@163.com。

TJ038;TH213.3

A

1004-499X(2017)03-0056-07