一種基于FTS車削的微切削力模型

謝曉麟，周曉勤，張新，張繼真，譚雙龍

（1.中國科學院長春光學精密機械與物理研究所 中國科學院光學系統先進制造技術重點實驗室，長春 130033；2.吉林大學 機械科學與工程學院，長春 130022）

一種基于FTS車削的微切削力模型

謝曉麟1，周曉勤2，張新1，張繼真1，譚雙龍1

（1.中國科學院長春光學精密機械與物理研究所 中國科學院光學系統先進制造技術重點實驗室，長春 130033；2.吉林大學 機械科學與工程學院，長春 130022）

機械加工中的切削力模型建立對于研究工件表面形貌成型，探究切削理論有著深遠的意義。在微切削加工領域，伺服車削通常用來加工自由曲面，但是考慮到尺寸效應，傳統宏觀領域的切削力模型無法真實地描述切削過程。針對微切削加工領域，提出了一種切削力模型，模型充分考慮了最小未成型切屑厚度，刀具切削刃鈍圓以及工件對后刀面回彈引起的摩擦力。由于切削深度不同，所對應的切削原理也不同，將切削過程分為多個區域建模。當刀具切入工件后，隨著切屑厚度的減小，切屑在前刀面分別經歷宏觀剪切、大負前角切削以及耕梨過程，而同時工件未切下的部分在后刀面的進一步作用下形成已加工表面，對應上述過程，將分為4個區域建模。最后，基于自主設計的能夠精確測量兩個方向切削力的快刀伺服裝置（DFT-FTS）設計實驗。

微切削力模型；快速刀具伺服；尺寸效應；自由曲面

對于機械加工，切削力是一個十分重要的參數。一直以來，切削力被認為與工件表面形貌成型的加工過程直接相關。加工表面形貌的優劣通常以粗糙度、毛刺以及面型誤差等作為判斷標準，伴隨著加工尺度越來越精細化，前兩者逐漸成為關鍵因素［1］。由于傳統模型是建立在剪切理論的基礎上，難以捕捉到上述兩個因素。因此，近年來建立能夠應用在微切削領域的切削力模型成為研究切削理論的焦點［2］。

Zvorykin等人奠基了傳統領域的切削力模型，后來經由Ernst、Merchant的研究，發展成為單剪切力平面模型，這些模型都是在宏觀尺度下進行探索，關注焦點是如何推導剪切角，其中一個較為有效的方法就是最小能量法。Lee和Shafer后來創新性地基于工程塑性力學分析金屬切削過程，推動切削理論產生新的發展。20世紀末，Dewhurst依據塑性理論建立滑移線場，分析金屬切削過程中工件的塑性變形，構造出滑移線切削模型。對于切削模型建立具有指導意義，對于切削理論的研究產生深遠影響，為解析型切削模型奠定了基礎。

但是，微尺度切削過程均無法通過上述模型直接描述，宏觀刀尖形狀如圖1所示。由于“尺寸效應”，微尺度切削過程切屑厚度極小，與刀尖切削刃鈍圓半徑數量級相當，如圖2所示，使得刀具進行大負前角切削，工件彈塑性變形并重［3］。切削力、切屑成型和厚度、加工表面成型質量等都受到尺寸效應的影響［4］。因此，刀尖切削刃鈍圓半徑成為微尺度下的關鍵，同時不能忽略最小未成型切屑厚度（MUCT）3，5-7］。在刀尖切削刃鈍圓圓周上對應MUCT的點被稱為“中性點”（neutral point）或“滯點”（stagnation point）。當背吃刀量小于MUCT時，切削過程主要體現為耕梨效應，而當背吃刀量大于MUCT，大負前角切削占主導。

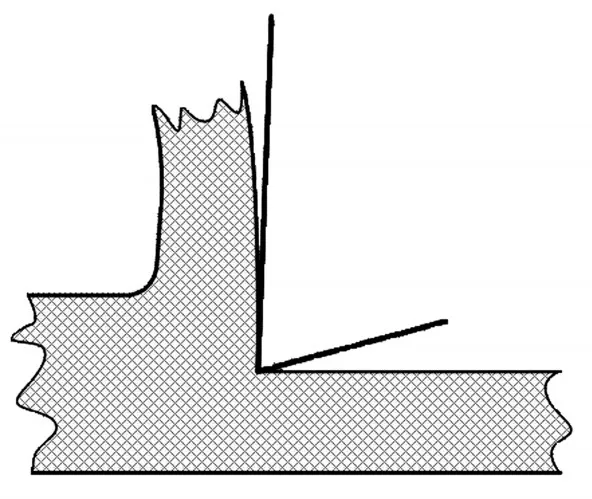
圖1 宏觀刀尖形狀

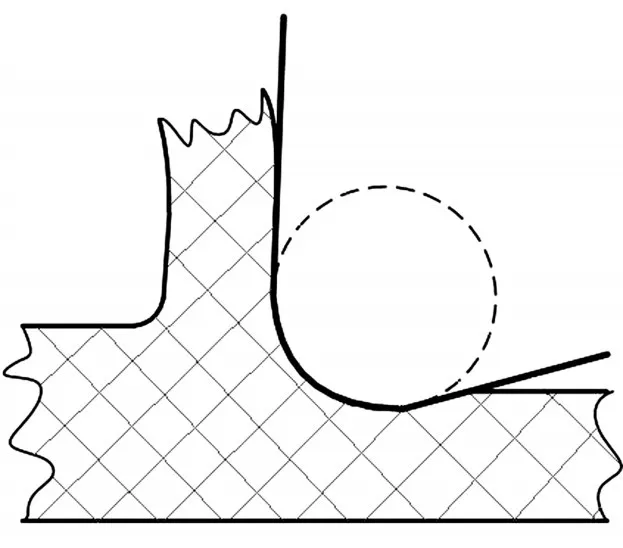
圖2 微切削尺度下刀尖形狀

對于微切削加工，耕梨力是切削力構成重要的部分之一。但是耕梨力模型該如何建立學者們還有很多爭議。現有兩種主要方法：滑移線理論模型［8-11］，如圖 3 和基于壓印效應的積分模型［3，12，13］，如圖4所示。

實際加工過程中，很多研究者注意到，刀尖切削刃鈍圓圓周前端會形成工件材料的堆積，類似于傳統領域切削的積屑瘤。因此，通過滑移線理論建立耕梨力模型通常基于如下假設，刀尖刃鈍圓處始終被工件材料形成一個三角形無限尖的堆積，并可視為“刀尖”，實際加工過程是以這個堆積刀尖在實現真正的切削。上述假設回避了刀尖刃鈍圓，認為工件材料在加工過程被鈍圓處堆積上的刀尖切割分流［7］。因此，直接應用傳統領域宏觀尺度下切削力模型，不需要積分。

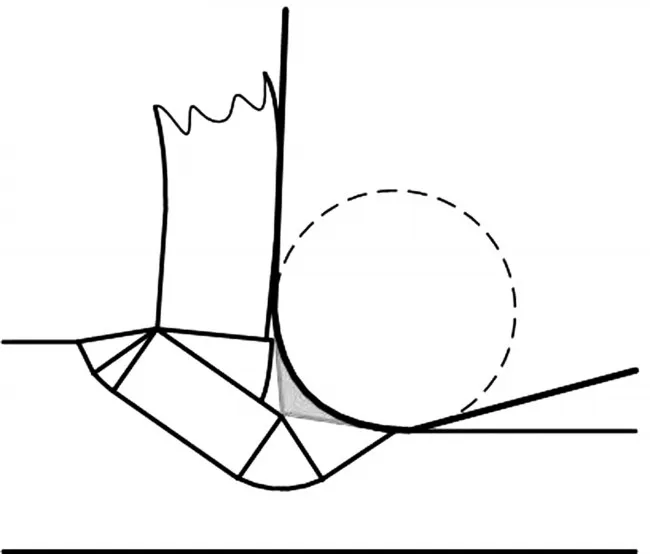
圖3 滑移線理論模型和

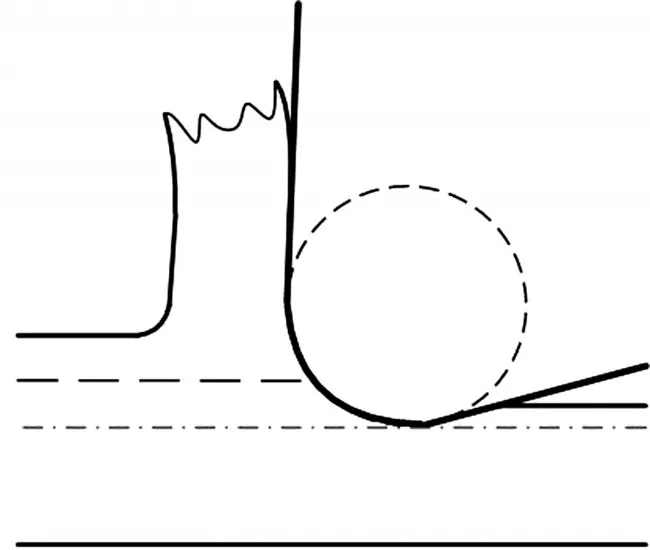
圖4 基于壓印效應的積分模型

而其他研究者認為，切屑直接與刀尖刃鈍圓發生作用，工件材料從滯點處切割分流，滯點以上的材料形成切屑流向前刀面，滯點以下的材料，在耕梨力的作用下流向后刀面，同時受到后刀面的擠壓發生弾塑性變形，最終形成工件表面。因此，耕梨力建模必須要包含擠壓作用，從而形成了基于壓印效應的模型［3］，其中切削力的分布沿著刀尖刃鈍圓圓周，需要通過積分運算進行模型。

考慮MUCT時，不同切削深度對應的切削原理不同，切削力由于性質不同易產生分類混亂。這種混亂對自由曲面微切削原理的研究影響更為嚴重。切削深度隨著自由曲面加工過程始終在變化，因此，針對不同切削深度進行建模尤為重要。近年來，隨著加工尺度精細化，微切削領域的相關研究越來越受到關注［14］。本文提出了如下微切削力模型。該預測模型對上述混亂進行了梳理，并同時將后刀面的影響也包含其中。

1 切削力模型

在切削過程中，刀具不同位置與工件接觸時會展現出不同的力學特性，因此，比較合理的切削力建模方法是分區處理。如Altintas［15］提出的切削力模型：

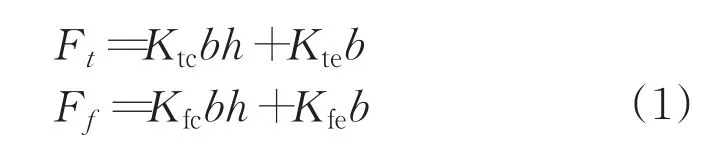
其中，Kte與Kfe表示刃口力系數，Ktc與Kfc表示切削力系數，b是切削寬度，h是切削深度。本文根據對應于不同切深的不同切削力特性進行系統明確的分區，如圖5所示。

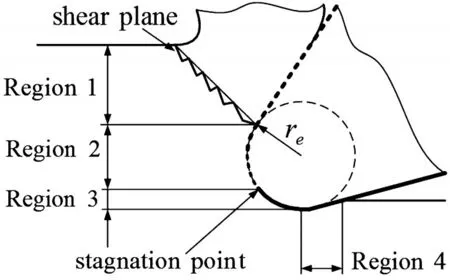
圖5 切削力建模分區圖

工件材料在滯點處被刀具分割，流向兩個方向。區域1和區域2處的材料流向前刀面，最終形成切屑，區域3和區域4處的材料流向后刀面，最終構成被加工表面。滯點可以等效于宏觀尺度切削中刀尖點。那么，刀具輪廓上位于滯點之上的部分，即鈍圓圓弧以上部分，在微切削尺度成為實際前刀面，見圖3粗虛線。刀具輪廓上位于滯點之下的部分，即鈍圓圓弧以下部分，可以作為實際后刀面，見圖3粗實線。綜合各區之和建立總的切削力模型。下面以切向力為例，基于正交切削條件，建立解析模型。

1.1 區域1（Region 1）模型

區域1的切削過程由前刀面部分完成，刀具鈍圓并沒有參與，除去分區后切削載荷的作用面積不同外，其他參數均未變，直接采用傳統宏觀尺度切削力模型進行計算。本文采用Merchant［16］的方法建立切削力模型：

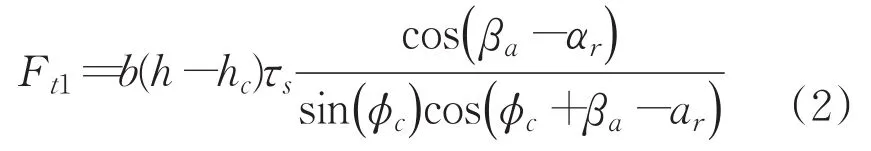
其中，h＞hc=(1+sinαr)re，τs表示工件材料屈服剪切應力，?c表示剪切角，βa表示摩擦角，αr表示刀具前角，hc表示前刀面與鈍圓弧相接點到刀具底部的垂直距離，如圖6所示。

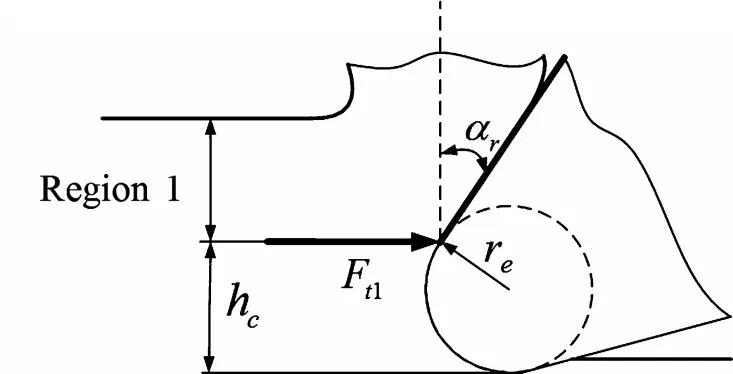
圖6 作用于區域1前刀面的切向切削力

1.2 區域2（Region 2）模型

區域2的切削過程由切削刃鈍圓弧滯點之上的部分完成，工作部分的每點的實際前角都不相同，隨著MUCT的減小，實際前角逐漸向大負前角過渡，如圖7所示。

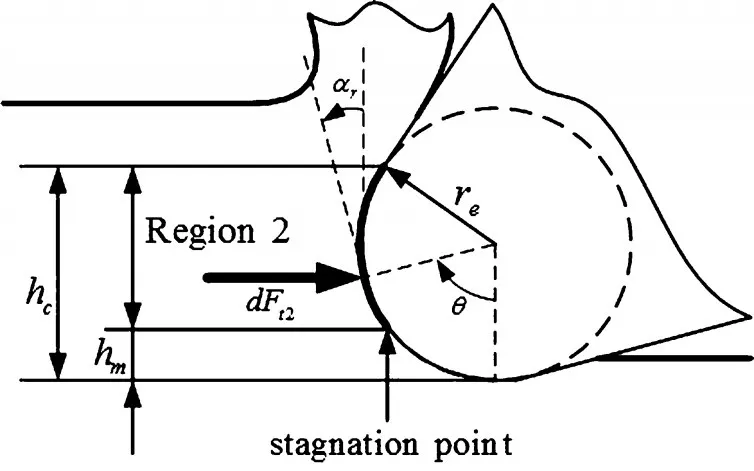
圖7 作用于區域2鈍圓弧上的切向切削力

每個未成型切屑厚度都對應著鈍圓的某個圓心角，根據幾何關系可得：

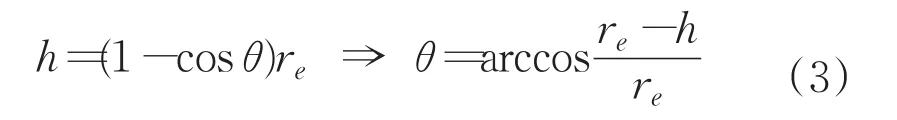
通過區域2對應的未成型切削厚度MUCT范圍能夠推到出角度變化范圍：

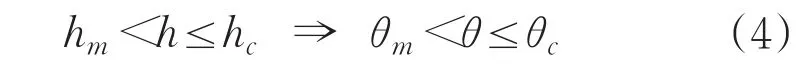
區域2鈍圓弧上某點的切削面積可表達為：

則區域2鈍圓弧上某點的切向力可表達為：

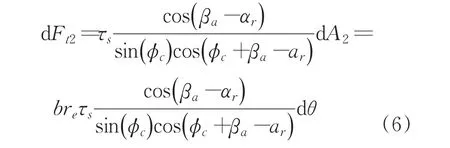
當θm＜θ≤θc時，由幾何關系有將其帶入上式可得到：

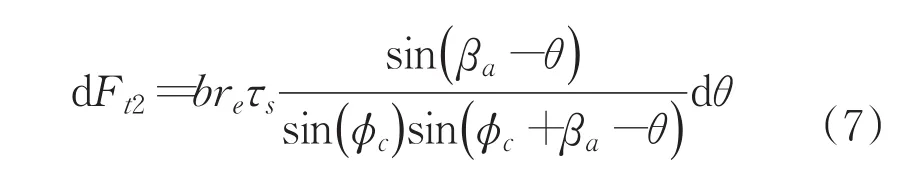
在整個區域2上對圓弧積分得出切向力：

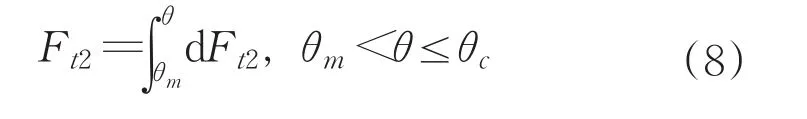
1.3 區域3（Region 3）模型

區域3的切削深度小于MUCT，并沒有產生實際切屑，只是工件表面被耕梨的過程。由切削刃鈍圓弧滯點之下的部分完成。在耕梨過程中，值得注意的是，并不是只有沿鈍圓圓弧的切向力作用，同時還有沿圓弧徑向的擠壓力作用在工件表面。擠壓作用使得工件材料產生弾塑性變形，對工件表面產生嚴重影響，如圖8所示。

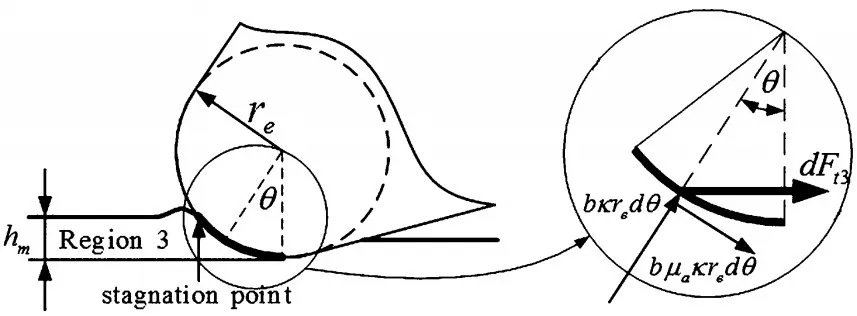
圖8 作用于區域3鈍圓弧上的切向耕梨力

因此，區域3鈍圓弧上某點耕梨力的切向分力可表達為如下兩部分：

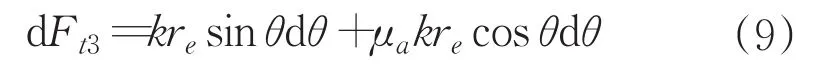
其中，k表示弾塑性變形的切削參數，單位為pa，為粘性阻尼系數。通過區域3切削深度得出相對應的圓心角范圍：

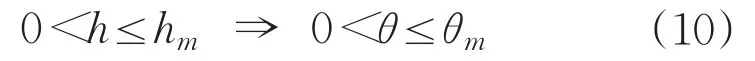
在整個區域3上積分得出耕梨力的切向分力為：

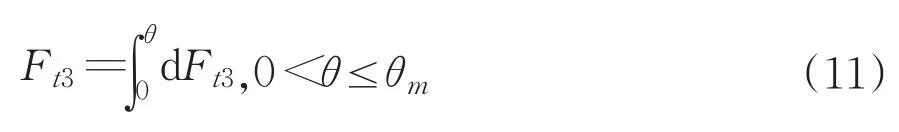
1.4 區域4（Region 4）模型

后刀面會抑制工件回彈變形，因而產生力的作用。后刀面對工件表面的作用，對于加工表面粗糙度以及殘余應力等都產生重要影響。因此在建立模型時需要充分考慮其影響［15，17］，尤其對于負后角切削建模更為關鍵［19，20］。

在考慮后刀面的影響時，一些學者將后刀面與鈍圓耕梨區域聯合處理［17］。另一些學者則在分析復合材料纖維方向同時，對后刀面部分切削力建模［19］。本文依據材料回彈特性建模。當工件材料經過刀尖鈍圓弧最低點后，會發生回彈變形。由于后刀面限制，回彈力將垂直的作用于后刀面上，并沿后刀面切向產生摩擦力，如圖9所示。

由胡克定律，后刀面上某點的回彈力可表達為：

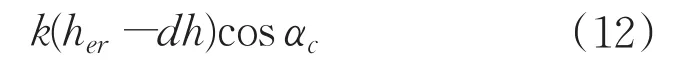
后刀面上某點與工件表面接觸產生摩擦力，表達如下：

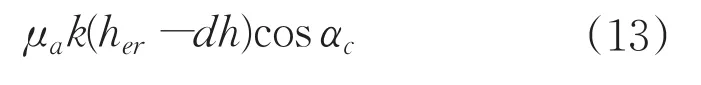
則可得到后刀面上某點的切向切削力力，如下：

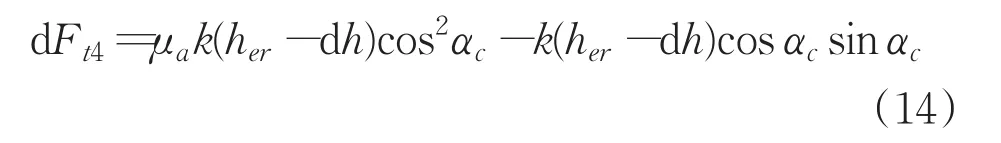
其中，k表示工件彈性系數，αc表示刀具后角。

對整個區域4進行積分得到切向力：

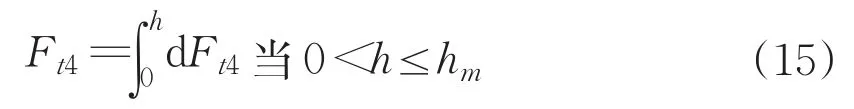
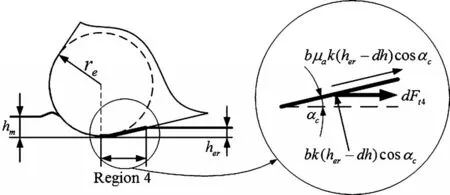
圖9 作用于區域4上的切向切削力力

1.5 綜合切削力模型

將各區切削力綜合起來，則總的切向切削力可表達為：

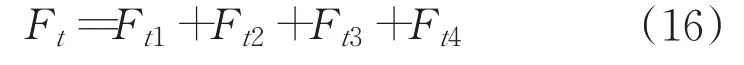
根據切削深度的變化，可以簡化如下：

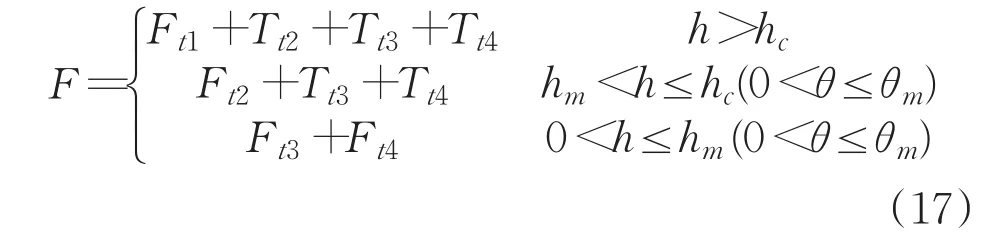
MUCT所對應的鈍圓圓心角的值取摩擦角βα［3］，帶入到上式中可得到更加簡化的形式，在此不再贅述。通過模型可以發現，除了耕梨過程，一旦切削深度增加到一定程度，微切削力將與切深呈現同種趨勢變化。在耕梨過程中，切削力則與切深呈現相反的趨勢，與“尺寸效應”現象相符合。

2 切削實驗

本文切削實驗基于德國Spinner SB/C TMC精密機床進行，該機床的超精密液壓主軸能夠實現微尺度級別的切削，如圖10所示。

如圖11所示，為自主設計的DFT-FTS，將其安裝在機床溜板上，可隨溜板實現沿機床x軸和z軸進給運動。加工工件時，溜板沿x軸產生恒定進給運動，同時快刀伺服系統由壓電驅動源沿z軸輸出高頻運動，從而加工工件周向形貌。采用人工合成金剛石（PCD）作為刀具刀尖材料，刀具半徑1mm，理論刀尖切削刃鈍圓半徑為200nm，前角0°，后角20°。本文設計兩種切削試驗，分別為了平面切削和自由曲面切削，切削工件均為鋁材。

圖10 Spinner SB/C TMC精密機床

圖11 能夠同時實現兩向切削力精確測量的快刀伺服裝置（DFT-FTS）

平面切削，設置機床主軸轉速400r/min，每轉溜板沿x軸的進給量10μm，通過控制機床z軸進給量使切削深度分別為100μm和20μm，記錄60s內的切削過程，得到的力信號見圖12和圖13。

圖12 切深為100μm平面切削時切削力測量值

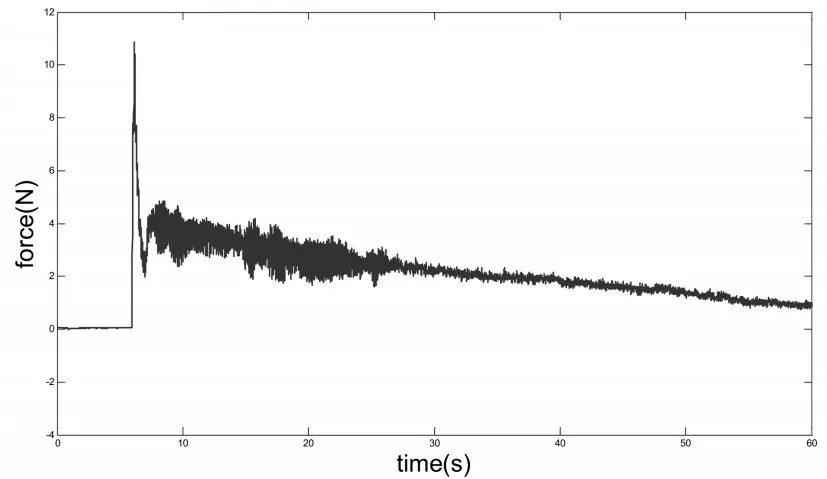
圖13 切深為20μm平面切削時切削力測量值

自由曲面切削，系統開環，由信號發生器對壓電驅動器提供正弦激勵信號。機床主軸轉速為同樣設置為400r/min，主軸每轉溜板沿x軸進給10μm，沿z軸進給50μm，通過機床沿z軸產生進給和快刀伺服裝置的壓電驅動，疊加形成刀具切削深度。在信號發生器輸出低頻正弦激勵時，60s內測得的力信號及切深分別如圖14和圖15所示。

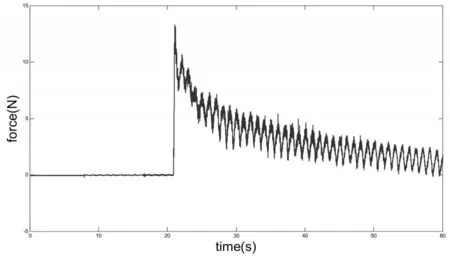
圖14 低頻正弦激勵下測得的力信號

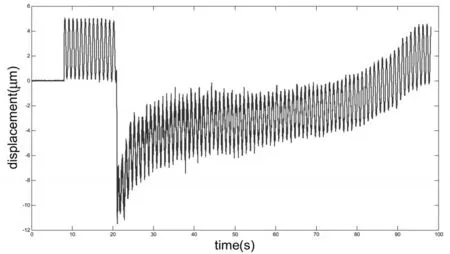
圖15 低頻正弦激勵下測得的切削深度

顯微鏡下所加工表面形貌如圖16所示。

圖16 顯微鏡下加工表面的形貌

微切削過程，切削量為幾個或十幾個微米情況下，切削力大體變化范圍為幾牛數量級，由于刀具刃口磨損會造成微進給時與工件表面接觸不良，為了避免上述情況，突出切削力的值，本文同時設置溜板輸出較大的切深進給。通過途中切削力的曲線可以看出，溜板切入大進給量的瞬間，切削力也出現很大的瞬態變化，直到溜板進給穩定后，切削力值才出現規律變化。隨著刀具沿x軸方向進給運動，主軸轉速不變情況下，等效切削速度在減小，從而切削載荷變小，切削力也呈現逐漸減小的總體趨勢。

通過本文建立的切削力模型可以發現，當切深增加，實際切屑厚度大于最小未成型切屑厚度時，切削力與切削深度同趨勢變化，而當切削發生在耕梨區內，切屑難以成型，這時切削力會與切深呈現相反趨勢變化。

3 結論

本文提出了一種切削力模型，將刀尖切削刃鈍圓和刀具后刀面對加工表面的擠壓作用都考慮其中，針對不同切深對應不同切削原理進行了分區建模，通過綜合模型描述切削力。

為了實現微切削力在線測量，研制了一種能夠同時測量兩方向切削力的快刀伺服裝置（DFTFTS），進行了實際加工過程中的切削力測量試驗，通過平面切削和自由曲面切削對模型進行驗證。

當刀具切入后，切削狀態穩定后，切削力與實際切深的關系與預測模型基本相符，切削力與切深呈現同種趨勢變化。但由于切入過程太快，外界噪聲等影響，對考慮刀具切削刃鈍圓的影響還需要進一步驗證。

［1］Aramcharoen A，Mativenga P T.Size effect and tool geometry in micromilling of tool steel［J］.Precision Engineering，2009，33（4）：402-407.

［2］謝曉麟.自由曲面伺服車削切削力測量及裝置研制［D］.長春：吉林大學，2015.

［3］Malekian M，Mostofa M G，Park S S，et al.Modeling of minimum uncut chip thickness in micro machining of aluminum［J］.Journal of Materials Processing Technology，2012，212（3）：553-559.

［4］Liu X，Devor RE，Kapoor SG，et al.The mechanics of machining at the microscale：assessment of the current state of the science［J］.Journal of Manufacturing Science&Engineering，2004，126（4）：5064-5070.

［5］Basuray P K，Misra B K，Lal G K.Transition from ploughing to cutting during machining with blunt tools.［J］Wear，1977，43（3）：341-349.

［6］Yuan Z J，Zhou M，Dong S.Effect of diamond tool sharpness on minimum cutting thickness and cutting surface integrity in ultraprecision machining［J］.Journal of Materials Processing Technology，1996，62（4）：327-330.

［7］Kim C J，Bono M，Ni J.Experimental analysis of chip formation in micro-milling［J］.NAMRI issue，2002，159（2）：1-8.

［8］Waldorf D J，Devor R E，Kapoor S G.A slip-line field for ploughing during orthogonal cutting［J］.Journal of Manufacturing Science&Engineering，1998，120（4）：693-699.

［9］Waldorf D J，DeVor R E，Kapoor S G.An evaluation of ploughing models for orthogonal machining［J］.Journal of Manufacturing Science&Engineering，1999，121（4）：550-558.

［10］Waldorf D J.A simplified model for ploughing forces in turning［J］.Journal of Manufacturing Processes，2006，8（8）：76-82.

［11］Pramanik A，Zhang L C，Arsecularatne J A.Prediction of cutting forces in machining of metal matrix composites［J］.International Journal of Machine Tools&Manufacture，2006，46（14）：1795-1803.

［12］Hyung Wook Park，Steven Y Liang.Force modeling of micro-grinding incorporating crystallographic effects［J］.International Journal of Machine Tools&Manuacture，2008，48（15）：1658-1667.

［13］Asma Perveen，Rahman M，Wong Y S.Modeling and simulationofcuttingforcesgeneratedduring vertical micro-grinding［J］.The International Journal of AdvancedManufacture，2014，71（9）：1539-1548.

［14］于占江，張超楠，王雯.表面溝槽微織構刀具高速微車削試驗研究［J］.長春理工大學學報：自然科學版，2015，38（03）：72-76.

［15］Altintas Y.Manufacturing automation：metal cutting mechanics，machine tool vibrations，and CNC design［M］.Cambridge：Cambridge University Press，March 2000：20-40.

［16］Merchant M E.Mechanics of the metal cutting process.I.Orthogonal cutting and type 2 chip［J］.Journal of Applied Physics，1945，16（5）：267-275.

［17］Park S S，Malekian M.Mechanistic modeling and accurate measurement of micro end milling forces［J］.CIRP Annals-Manufacturing Technology，2009，58（1）：49-52.

［18］Zhang L C.Cutting composites：A discussion on mechanics modeling［J］.Journal of Materials Processing Tech，2009，209（9）：4548-4552.

［19］Transchel R，Leinenbach C，Wegener K.Cutting and ploughing forces for small clearance angles of hexaoctahedron shaped diamond grains［J］.CIRP Annals-Manufacturing Technology，2014，63（1）：325-328.

［20］李曉舟，于化東，許金凱，等.微切削加工中切削力的理論與實驗［J］.光學精密工程，2009，17（5）：1086-1092.

A Micro Cutting Force Model Based on FTS Turning

XIE Xiaolin1，ZHOU Xiaoqin2，ZHANG Xin1，ZHANG Jizhen1，TAN Shuanglong1
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，Key Laboratory of Optical System Advanced Manufacturing Technology，Chinese Academy of Sciences，Changchun 130033；2.School of Mechanical Science and Engineering，Jilin University，Changchun 130022）

The establishment of cutting force model in machining is of great significance to study the surface morphology of workpiece and explore the cutting theory.Due to the so-called size effect，the cutting force model in the traditional field can not be directly applied to the micro-machining of free-form surface servo turning.In this paper，a cutting force prediction model for micro-cutting is proposed.The model gives full consideration to the factors such as the cutting edge of the cutting edge of the tool，the minimum unformed chip thickness and the frictional force generated by the flank return force.Due to the different cutting depth the cutting principle is different，the micro cutting force model will be developed according to different region.Finally，the experiment is designed based on the micro servo turning with self-designed a dual-axis force transducer-embedded fast tool servo（DFT-FTS） device.

micro cutting force model；fast tool servo；size effect；free form surface

TG501.3

A

1672-9870（2017）04-0001-06

2017-05-08

謝曉麟（1988-），男，研究實習員，E-mail：xiexiaolin1988@