企業(yè)合作融資行為博弈分析

【摘要】企業(yè)間合作融資是解決當前我國融資問題的一種有效方式，而在何種環(huán)境下更有利于這種合作的發(fā)生是一個值得深思的問題。集群的發(fā)展為這一問題提供了新思路。本文研究的重點在于運用各種博弈模型通過揭示合作融資行為選擇的耦合過程，證明集群是合作融資行為發(fā)生的優(yōu)勢環(huán)境，并進一步分析如何塑造有利于集群企業(yè)合作融資行為產(chǎn)生條件。

【關鍵詞】企業(yè)；合作融資；博弈；集群

一、引言

當前中小企業(yè)普遍面臨融資困難以及各種解決途徑的低效性狀況，而當生活中的人們面臨一種共同危機時，彼此之間就會有同病相憐的感覺，此時的人們就容易形成一種共同對抗的意識。而在地理相鄰或環(huán)境相近的情況下，就更容易導致他們之間合作的發(fā)生。而我國目前的中小企業(yè)就處在這樣一種狀態(tài)下，因此“抱團”合作融資成為解決他們?nèi)谫Y困境的首要方法。合作融資就是在民間商會或焦點企業(yè)的組織下，一群產(chǎn)業(yè)關聯(lián)、相互了解且有融資需要的中小企業(yè)按照自愿加入、民主管理、互助互利的原則建立合作組，統(tǒng)一向外界融資的合作融資制度，是產(chǎn)業(yè)和空間集聚優(yōu)勢應用于融資活動的結(jié)果。（曾繁英，2008）由于集群內(nèi)企業(yè)之間存在著地理的鄰近性，合作的網(wǎng)絡性和交易的長期和重復性的優(yōu)勢，這就使得合作融資基本上在集群內(nèi)發(fā)生。單個企業(yè)融資困難主要是由于是自身信用狀況不佳所致，而集群合作融資通過組建各種信用合作平臺來提升企業(yè)的信用，進而解決企業(yè)的融資問題。兩者的主要差別在于合作融資是一種集體行動，合作方為了共同利益而努力。

我國對于集群合作融資理論的研究主要側(cè)重于規(guī)范方面的研究，如張丙坤、馬建會（2003）研究了中小企業(yè)集群具有相對單個中小企業(yè)的獨特融資優(yōu)勢。陳曉紅等人分析了合作融資的運行機制，并歸納出各種集群合作融資方式 ，如集合發(fā)展模式、互助融資擔保模式以及“鳥巢”模式等。在實證方面也有少量的研究成果，如胡紅桂從實證的角度檢驗了中小企業(yè)集群融資效率高于非集群企業(yè)的融資效率，并同時分析了集群企業(yè)融資效率的影響因素。而對于集群合作融資過程中行為主體之間的博弈分析則主要是有關銀企間的博弈分析，如樓瑜、程路（2006）以紹興輕紡產(chǎn)業(yè)集群為例對集群企業(yè)與銀行的關系型融資互動關系進行了實證分析，認為在集群條件下銀企關系有了新的表現(xiàn)，并且正是基于集群特征而產(chǎn)生的集群信息機制、成本降低機制以及長期動態(tài)重復博弈機制帶來了集群獨特的融資效率。因此，從我國目前的研究現(xiàn)狀來看，對于集群合作主體的行為分析甚少，而對于為什么集群是適合企業(yè)合作融資的環(huán)境的研究多為文字方面的探討，沒有從一個合作行為博弈的分析過程中剖析這樣一個耦合的過程。而企業(yè)作為合作融資的關鍵主體，更有必要和意義對其行為進行分析。因此本文利用合作博弈模型分析合作融資過程中企業(yè)的行為選擇，并進一步剖析如何塑造有利于集群企業(yè)合作行為產(chǎn)生的條件。

二、模型的構(gòu)建與分析

合作融資是解決企業(yè)當前融資困境的主要方法，而合作融資作為一種集體行動就避免不了各參與者的搭便車行為產(chǎn)生。假設取參與合作融資的兩個均質(zhì)企業(yè)1和2，企業(yè)的行為分為合作與搭便車兩種，其中合作是指企業(yè)為合作融資做積極的努力。當雙方均采用搭便車行為時，合作融資失敗，雙方受益均為0；當企業(yè)一方努力，另一方搭便車時，合作融資成功的可能性降低，本文設其表現(xiàn)形式為融資量的減少，另外融資成本全由努力方承擔；只有當雙方均努力時，合作融資才能的效果才能達到最優(yōu)。企業(yè)與企業(yè)之間的合作行為是為了解決企業(yè)融資困境的一種集體行動，類似于公共產(chǎn)品的供給。本文博弈模型的構(gòu)建主要參考胡擁軍、毛爽（2011）在分析農(nóng)村社區(qū)公共產(chǎn)品合作供給時所用的方法。

（一）企業(yè)間的一次性博弈

在不考慮其他企業(yè)行為和投資風險的情況下，設企業(yè)投資回報率均為r，該合作融資能給企業(yè)帶來的融資量為Q，融資總成本為C，凈收益Qr-C>0。如果雙方合作，每一方的凈收益為（Qr-C）/2；如果一方搭便車，另一方合作，則取得的融資量為q，q

由該支付矩陣可知，當Qr-C

（二）完全信息條件下重復博弈模型

完全信息（張維迎，2004）是指自然不首先行動或自然的初始行動被所有參與人準確觀察到的情況，即沒有事先的不確定性。根據(jù)無名氏定理①，如果參與人有足夠的耐心，無限次重復博弈存在著完全不同于一次博弈的子博弈精煉均衡，既（合作，合作）。這也是企業(yè)間的合作融資行為博弈的均衡結(jié)果。模型分析如下：

假定1，企業(yè)在長期的交往中形成了一種共同的規(guī)范：所有企業(yè)為了共同的融資目標都應該參與合作；一旦有人搭便車，其他成員將永遠不與他合作。這就是博弈論中所指的冷酷戰(zhàn)略：（1）開始選擇合作；（2）選擇合作直到有一方選擇了搭便車，則一直選擇搭便車。

假定2，貼現(xiàn)因子為δ，0≤δ≤1企業(yè)的獲得的利益是各期收益的總現(xiàn)值。

假定3，取兩個均質(zhì)企業(yè)1，他們之間的單期博弈關系表如表1所示。

在以上這些條件下，如果企業(yè)1在博弈的某個階段首先選擇搭便車，那么他在這期收益為qr/2，因為信息完全且企業(yè)2采用的是冷酷戰(zhàn)略，所以企業(yè)1一旦選擇搭便車則會永遠搭便車，以后各階段的收益將均為0；如果企業(yè)一直選擇合作，則他在各期的收益則一直為（Qr-C）/2。因此，當滿足以下條件時，企業(yè)1或2將永遠不會選擇搭便車：

qr/2≤（Qr-C）/2+δ（Qr-C）/2 +δ2 （Qr-C）/2 +…

化簡為：δ≥1-（Qr-C）/qr

由此可知，如果滿足δ≥1-（Qr-C）/qr，在給定企業(yè)2選擇冷酷戰(zhàn)略且首先選擇合作行為，則企業(yè)1不會首先選擇搭便車行為。同理，在給定企業(yè)1選擇冷酷戰(zhàn)略且首先選擇合作行為，則企業(yè)2不會首先選擇搭便車行為。因此，在完全信息條件下的無限次重復博弈的均衡結(jié)果為（合作，合作）。這就證明了，當滿足δ≥1-（Qr-C）/qr，則冷酷戰(zhàn)略是該博弈的均衡結(jié)果，這就克服了有限次重復博弈中的搭便車行為。

（三）不完全信息條件下的重復博弈模型

以上分析是在完全信息的條件下進行的，這是比較理想的模型，事實上，在要想完全清楚地知道博弈方的類型是比較難的事情，企業(yè)更多的是處在不完全信息環(huán)境下的，因此本文將采用聲譽模型（簡稱KMRW模型）進一步論證在不完全信息下條件下的重復博弈的均衡結(jié)果。

假定合作企業(yè)1有兩種類型，理性的和非理性的，概率分別為（1-p）和p，在這里理性企業(yè)可以理解為機會主義企業(yè)。假定理性的企業(yè)可以選擇任何戰(zhàn)略，階段博弈的支付矩陣如表1所示。非理性的企業(yè)，由于某種原因，只有一種戰(zhàn)略，即“針鋒相對”：開始選擇合作，然后在t階段選擇企業(yè)2在t-1階段的選擇（即你合作我合作，你搭便車我搭便車），本文將它視為合作型的企業(yè)。為簡單起見，假定企業(yè)2只有一種類型，即理性的，也就是機會主義企業(yè)。根據(jù)有限次重復博弈的理論可知，機會主義企業(yè)在博弈的最后階段均采用搭便車。（張維迎）博弈的順序如下：

（1）自然首先選擇企業(yè)1的類型；企業(yè)1知道自己的類型，企業(yè)2只知道企業(yè)1屬于理性的概率是（1-p），非理性的概率是P；

（2）兩個企業(yè)進行第一階段的博弈；

（3）觀測到前一階段的博弈結(jié)果后才進行下一階段的博弈，如此等等；

（4）企業(yè)1和企業(yè)2的支付是階段博弈支付的貼現(xiàn)值之和。貼現(xiàn)因子為δ，為了方便計算，假定δ=1。

首先討論博弈只重復兩次的情況。根據(jù)以上假定條件，博弈結(jié)果如表2 所示，當選擇X為合作時，企業(yè)1的期望支付水平為：p[（Qr-C）/2+qr/2]+（1-p）[（qr/2-C）+0]；當選擇X為搭便車時，企業(yè)1的期望支付水平為：pqr/2。因此，如果滿足下列條件，企業(yè)1在第二階段將選擇合作：

p[（Qr-C）/2+qr/2]+（1-p）[（qr/2-C）+0]≥ pqr/2，

即p≥（2C-qr）/（Qr-qr+C）。

以上分析說明如果企業(yè)1屬于合作型的概率不小于（2Cqr）/（Qr-qr+C），則企業(yè)2雖然是機會主義者，但是為了獲得高支付水平，依然有動力在第一階段選擇合作行為。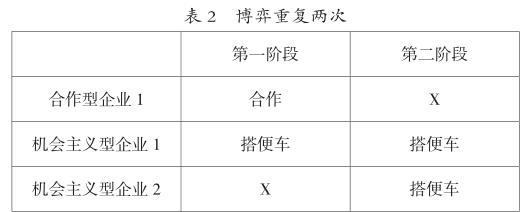

其次考察博弈重復三次的情況，在以上分析的基礎上，給定p≥（2C-qr）/（Qr-qr+C），由于博弈重復三次，且合作型企業(yè)在第一階段均會選擇合作，所以機會主義企業(yè)1如果在第一階段選擇搭便車，那就暴露了他是機會主義型的，導致機會主義企業(yè)2在以后各期的搭便車行為，因此為了隱藏自己的類型，機會主義企業(yè)1的選擇為（合作，搭便車，搭便車）。合作型企業(yè)1首次選擇合作，以后的選擇與前階段企業(yè)2的選擇相同。機會主義型企業(yè)在最后階段的選擇均為搭便車（根據(jù)有限次重復博弈理論）。博弈結(jié)果如表3所示。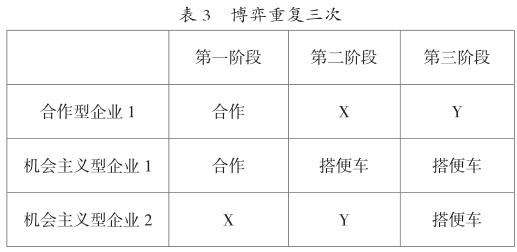

當企業(yè)2首次選擇X=合作，則由于p≥（2C-qr）/（Qrqr+C），為了使二、三階段獲得更高的支付，則需滿足Y=合作。對應企業(yè)2的三階段的選擇為（合作，合作，搭便車）。此時，企業(yè)2的期望支付為：

p [（Qr-C）/2+（Qr-C）/2+ qr/2]+（1-p）[ （Qr-C）/2+（qr/2-C）+0]；

當企業(yè)2首次選擇X=搭便車時，Y的選擇仍然有兩種情況：合作或搭便車。第一種情況取Y=合作時，則企業(yè)2三個階段的選擇為（搭便車，合作，搭便車）。此時，企業(yè)2的期望支付為：

p[qr/2+（qr/2-C）+0]+ （1-p） [qr/2+（qr/2-C）+0]；

當X=搭便車時，第二種情況取Y=搭便車，則企業(yè)2三階段的選擇為（搭便車，搭便車，搭便車），此時，企業(yè)2的期望支付為：

p[qr/2+0+0]+ （1-p） [qr/2+0+0]=qr/2

由于p≥（2C-qr）/（Qr-qr+C），經(jīng)計算可知，企業(yè)2在（合作，合作，搭便車）的戰(zhàn)略選擇下的期望收益明顯高于另外兩種戰(zhàn)略。所以在博弈重復三次的情況下，企業(yè)2的最優(yōu)策略為（合作，合作，搭便車）。

最后，同理將博弈的重復次數(shù)推廣至大于3的情況下時，合作型企業(yè)1會一直選擇合作；機會主義企業(yè)1的選擇則是開始堅持選擇合作，到最后兩期選擇搭便車；機會主義企業(yè)2則會一直堅持選擇合作直到最后一期才選擇搭便車。所以，在不完全信息下博弈的環(huán)境下，企業(yè)無法確定合作方類型時，由于害怕合作型企業(yè)的“針鋒相對”戰(zhàn)略，所以他也會在相當長的時間內(nèi)表現(xiàn)為合作型的。

（四）博弈小結(jié)

從以上三個合作融資的博弈模型中我們可以看到，企業(yè)間如果是單次博弈，若Qr-C

三、合作融資環(huán)境與條件分析

根據(jù)以上博弈的結(jié)果推知，構(gòu)建企業(yè)間長期的合作關系是促成企業(yè)間合作融資成功的關鍵。而一般的企業(yè)之間多處于一種互無往來關系的，類似于“原子化社會”②，此時企業(yè)之間的合作融資的博弈模型就是單次博弈模型。而集群內(nèi)的企業(yè)之間存在著緊密的聯(lián)系，企業(yè)的互動行為也是長期而非一次性的。這主要與集群的特征相關，集群內(nèi)企業(yè)受社會資本的影響，各企業(yè)成員之間有著共同的生存方式和歷史傳承，如文化習慣、生產(chǎn)協(xié)助、生活交往等諸多的綜合因素。在這樣的一個環(huán)境下，企業(yè)之間就會形成長期的交易往來，企業(yè)與企業(yè)之間的博弈也就與集群外的企業(yè)完全不同 ，集群外的企業(yè)之間是一次性的博弈，而集群內(nèi)的則是長期重復的博弈。因此，集群環(huán)境是企業(yè)合作融資行為的優(yōu)勢環(huán)境。也就是說，集群企業(yè)間的合作融資比較非集群企業(yè)而言，能夠更為有效得地避免這種集體行動中的搭便車行為，從而更容易達到合作融資的最優(yōu)效果。

而通過對兩種信息下重復博弈最優(yōu)策略的條件分析，我們可以得出如何在集群環(huán)境下促成最優(yōu)策略的發(fā)生。

第一，當企業(yè)處于完全信息下時，需要滿足的條件是δ≥1-（Qr-C）/qr，當貼現(xiàn)因子δ越大，說明企業(yè)對未來收益的期望值也就越高時，企業(yè)就越有動機維持自己一個愛合作的好聲譽以獲得未來的高支付；反之，則意味著企業(yè)對未來收益的期望值較低，當δ=0時，企業(yè)就已經(jīng)完全不在乎未來的收益了，此時就具備強烈的搭便車行為，這也部分的解釋了單期交易的企業(yè)之間難以實現(xiàn)集體行動的原因。因此，要想使該條件成立，就要提高δ，也就是提高企業(yè)對未來的預期收益率。

第二，當企業(yè)處于不完全信息下時，根據(jù)最優(yōu)策略成立的條件p≥（2C-qr）/（Qr-qr+C），可知，P為企業(yè)1為非理性類型——合作型的概率，該企業(yè)采用的是“針鋒相對”的策略。設Y=（2C-qr）/（Qr-qr+C），則dY/dr=（cq-2QC）/（Qr-qr+C）2，由于q0，所以融資成本C與Y成正相關關系。因此，要使條件p≥（2Cqr）/（Qr-qr+C）成立的可能性增大，可取的方法有兩種，一是加大P，二是減小Y=（2C-qr）/（Qr-qr+C）。而投資回報率r與Y負相關，即r越大時，Y越小；融資成本C與Y成正相關，即C越小時，Y越大。所以減小Y的方法可以通過提高r和降低C來實現(xiàn)。

四、結(jié)論

綜上所訴，中小企業(yè)在共同面臨融資困境這樣的難題時，集群外的單個企業(yè)與企業(yè)之間要想建立合作關系是比較困難的，該情況類似于以上我們所講的“原子化社會”下兩企業(yè)之間的合作博弈。而當企業(yè)處在集群這樣一個環(huán)境下的時候，不管是完全信息下的重復博弈還是不完全信息下的重復博弈，只要合作次數(shù)無限，合作融資就會發(fā)生。因此，本文認為集群環(huán)境是促進合作融資成功的有效保障。

另外在集群環(huán)境下可以通過以下幾個方面來提高合作融資成功的可能性：

第一，在完全信息下，可以通過提高企業(yè)對未來預期的收益來提高合作融資成功的概率，也就是說要培養(yǎng)企業(yè)的長遠目光。第二，培養(yǎng)企業(yè)的合作意識，使企業(yè)的類型更多的傾向于合作型企業(yè)，而非機會主義型企業(yè)，也就是讓企業(yè)之間建立一種較為信任的關系。第三，提高企業(yè)的投資回報率r和降低企業(yè)的融資成本。投資回報率的提升主要是靠企業(yè)自身的努力，而融資成本的降低還需要依賴政府、銀行、行業(yè)協(xié)會或其他中介組織的支持。

注釋：

①最初又稱為“納什無名氏定理”，它考慮的是無限次重復博弈納什均衡的情況。

②該思想最初出現(xiàn)于馬克思的“馬鈴薯理論”，意思是所有原子雖然構(gòu)成了一只一個物整體，但它們彼此之間是相互獨立且不相干的。

參考文獻

[1] 曾繁英.企業(yè)集群治理及其投融資合作研究[D].長沙：湖南大學，2009.

[2] 張丙坤，馬建會.改進我國中小企業(yè)集群融資的對策分析[J].經(jīng)濟經(jīng)緯，2003（05）.

[3] 陳曉紅，楊懷東.中小企業(yè)集群融資[M].北京：經(jīng)濟科學出版社，2008（05）.

[4] 胡紅桂.中小企業(yè)集群融資效率研究[D].長沙：中南大學，2008.

[5] 樓瑜，程璐.集群企業(yè)與銀行的關系型融資的實證分析[J].上海金融，2004（08）.

[6] 胡擁軍，毛爽.農(nóng)村社區(qū)公共產(chǎn)品合作供給的決策機制——基于“熟人社會”的博弈框架[J].蘭州學刊，2011（01）.

[7] 張魁偉，許可.產(chǎn)業(yè)集群的社會資本運行機制[J].經(jīng)濟學家，2007（04）.

作者簡介：陳芳（1987.01—），女，漢族，湖南益陽人，碩士，助教，研究方向：公司財務治理。