逐層細剝筍，矛盾漸統一
——以《用數對確定位置》的教學為例

江蘇南京市溧水區烏山小學 許祥薇

江蘇南京市溧水區教研室 吳義明

逐層細剝筍，矛盾漸統一
——以《用數對確定位置》的教學為例

江蘇南京市溧水區烏山小學 許祥薇

江蘇南京市溧水區教研室 吳義明

學習本應是主動的、富有個性的過程，可往往因缺少需求而變成被動的、灌溉式的程序。本文以《用數對確定位置》為例，基于對學生起點的了解激發需求，并以需求為依據不斷創生矛盾，讓學生在解決層層矛盾時體驗新知的產生,以矛盾激需求，在矛盾中體現統一，讓學習變得更有意義。

數對 矛盾 需求 統一

將一個陌生的知識硬生生地放在學生面前，并要求他們必須去學習，這時他們常常會嘀咕：“我為什么要學這個？這么麻煩？”此時被動接受、無奈吸收就成為這些學生的寫照。“被動”轉“主動”，“無奈”轉“欣喜”，筆者認為激發起學生對新知的渴求是關鍵，而渴求往往產生于解決不了的矛盾之中。要讓學生在體會矛盾、解決矛盾的過程中產生對新知的渴求，教師首先要清楚他們的學習起點。正如奧蘇貝爾所指出：“影響學習最主要的原因是學生已經知道了什么”。

教師在教學“確定位置”時，以游戲的形式引導學生學習。在活動中創生多重矛盾，矛盾層層遞進，直至確定位置的核心和本質；并在矛盾中解決矛盾，在產生的新矛盾中再解決新的矛盾……直到顯露出事物的本質，最后達到矛盾的統一。

第一層，“你寫我猜”，制造認知沖突

師：班上有你敬佩的人嗎？能不能把他的位置記下來。

學生選擇自己喜歡的方式來確定位置。交流展示（見圖1），并讓其他學生根據這些描述猜一猜到底是誰。

圖1

學生從“西北”到“左面的前面”再到“第二組第八個”，范圍在不斷縮小，真相在慢慢接近。在猜的過程中，讓學生回顧了“東南西北”“前后左右”“第幾第幾”這些已經熟悉的方位詞。學生們在對比這些確定位置的方法時發現：要清楚確定一個人的位置至少需要兩個數量。

引以為傲的舊知在“說清楚”的面前出現了第一次的不滿足。這讓學生產生認知沖突：為什么以前很好用的方法今天卻無法說清楚自己想要描述的那個人的位置呢？教師激發學生反思舊方法中存在的缺陷，為接下來列、行的學習埋下伏筆。

第二層，“我說你寫”，引出方向矛盾

師：重新選擇描述方式，記錄“A的好朋友B的位置”，要求盡可能地簡單又清楚。

通過“你寫我猜”的環節，這次學生們幾乎都選擇了“第幾第幾”的方式來描述，但描述詞五花八門。對比同一種描述發現，即使都是以“第幾組第幾個”來描述，仍出現了位置的不統一。原來在確定“組”“個”的左右方向、前后方向時，學生各執一詞。由此學生感受到“數字”和“方向詞”結合才能準確地確定位置。

可是選擇什么“詞”來描述，“方向”如何規定才更合理、更具說服力呢？學生開始動腦筋，尋求幫助。有的進行小組商議，考慮是否進行內部人為規定；有的求助老師；有的開始查閱課本資料等。感覺可以“說清楚”了，可就是差那么一點點。在學生最需要幫助的時候，拉學生一把，猶如雪中送炭，學生將記憶深刻。

師：描述中“第3組”“第4個”，這里的“3”和“4”都表示什么？

生：“3”指的是第3豎排，“4”指的是第4橫排。

師：在數學中，我們把豎排統稱為“列”；相對的，橫排數學上統稱為“行”。

在統一了“第幾列第幾行”這樣的描述后，學生隨即提問：“那列與行的方向呢？”教師認為數學學習的重要方式不僅僅是接受學習，還有主動思考、自主探究與合作交流。既然學生發現了問題，就應該給他們空間與時間去解決問題。所以教師反問道：“那你們討論一下，覺得它們的方向該如何確定是最合適的？”學生對此展開激烈地爭論，然后闡述各自小組討論后的結果。最后學生們認為：按照現在讀書的順序、一般計算的順序都是“從左往右”，所以他們認為“第幾列”應該也是從左往右確定的；按照同學的生活經驗，數“行數”都是從前往后數，所以他們認為“第幾行”應該是從前往后確定的。

方向的確定由被動地接受“人為規定”轉變為自我創造“人為規定”，讓學生體驗規定的過程，在解決矛盾中達到統一。所謂“學”就是自我解決問題。

第三層，“請你畫畫”，導出觀察各異

師：請你畫一畫本班的座位表，并且用新學到的確定位置的方式標出自己的位置以及你好朋友的位置。

圖2

座位圖出現了以上兩種形式（見圖2的a與b），以講臺為參照，兩幅圖中的“列”都是從左往右確定的，“行”也都是從前往后數確定的，可是對同一個人的描述仍出現了分歧（見圖3）。

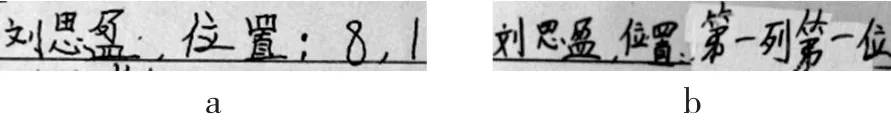
圖3

對比反思，造成這樣的不統一主要源于觀察者的位置不同。圖2a中學生以自己的視角來描述座位圖，講臺在他的前面；而圖2b中學生以站在教室中講臺的位置為觀察點，即以教師或第三者的位置為觀察點。從這樣的對比中，學生發現即使描述方式、方向都已經約定，但因觀察的位置不同，仍會產生分歧，造成誤解。這樣的不統一啟發學生思考描繪座位圖的目的是什么？學生換位思考，重新繪座位圖。

經過3輪的矛盾沖擊，學生從雜亂無章到統一有序，遇到問題主動解決，在需求中探索新知，重新認識“確定位置”。但數學總是以簡潔為美，少部分學生（見圖3a）已經產生簡單記錄的萌芽，教師需要進行強化以激發所有學生的“需求”。

第四層，“位置快閃”，尋找化繁為簡

師：學習完“第幾列，第幾行”，想必我們大家都能用這種方法來確定同學的位置了吧？這里有一些同學喜歡玩快閃，你能不能準確地抓住他們呢？在練習紙上，記錄下你看到的同學的位置。

屏幕上“快閃”情境圖中出現4個同學的位置。多數學生還沒反應過來，動畫已經播放結束，只能憑著記憶寫下印象最深的那一兩個。短短的時間里在情境圖中不僅要觀察位置的變化還要準確記錄位置，這樣的要求讓學生覺得有些困難。

師：你們遇到了什么困難？

生1：速度太快。

師：那你想……

生1：再放一遍。

生2：畫面太復雜。

師：那你想……

生2：去掉人物，用圓圈代替這里的同學。

生3：描述位置時我們要寫的字太多，時間不夠。

師：那你想……

生3：我們得想想哪些字可以省略。

遇到問題去主動分析，一一擊破，這才是學習該有的模樣。

按照學生的要求，教師再放一遍，并且將課本情境座位圖變為點子圖。沒有了座位、人物形象的影響，學生個個躍躍欲試。

終極賽結束，所有的學生經過自己的努力都有了屬于自己的記錄結果（見圖4）：有的給自己出了“填空題”，即在我們討論的間隙，提前寫好了所有的“第（ ）列，第（ ）行”；有的找到課本里的情境圖；有的快速地將簡化座位圖在練習紙上描繪出來；還有的在快閃的人名旁邊按順序只記錄下兩個數字等。

圖4

反饋交流，一起評判各自記錄結果的優點與缺點。最后明確：圖4c是最方便、有效的記錄方式。因為前幾種方法都是利用大家談論的間隙去尋找、補充的。如果只有一次快閃機會，前幾種方法肯定會以失敗告終。圖4c能這樣記錄，前提是大家都認可了“第（）列第（）行”的描述方式，所以第1個數字表示的是“第幾列”，第2個數字表示的是“第幾行”。僅僅兩個數字就能準確地確定位置，這是數學簡潔的美與妙。

最后，在學生總結的基礎上，教師規范了記錄方式，并明確：像（1,2）這樣用來描述位置的一組數，我們數學上叫它為‘數對’”。

學生從層層矛盾中體驗到了“數對”產生的過程，從需求中應生了統一的規則。數學的教學不能僅僅停留在“讓學生學習有價值的數學”，而是“讓學生接受數學教育”，從過程中去體驗數學的價值、去經歷“數學思維”的升華。在體驗數學的過程中，我們不應生硬地“拽”著學生跟隨教學設計而“表演”，而是應從學生的需求開始，讓學生在層層矛盾與需求中體驗“約定俗成”的數學方法或定理的產生過程，在不斷解決矛盾中碰撞數學的思維。?