“慢”課堂,慢在學生思維中
江蘇鹽城市一小教育集團聚亨路校區 朱麗萍
“慢”課堂,慢在學生思維中
江蘇鹽城市一小教育集團聚亨路校區 朱麗萍
每個學生在數學學習過程中是存在差異的,為了讓每個學生在數學學習中自信而幸福,教師應該更加關注學生的數學思維,使學生在思維困惑處、錯誤處和生長處得到數學智慧的發展。
數學課堂 學生思維 慢教學
學生是一個個活生生的人,每個學生都是一個獨立的個體,他們都有不同的數學思維,都渴望在數學上得到良好的發展。因此,數學教師在課堂上要遵循學生的自然發展規律,多給學生時間和機會,讓他們在原有的基礎上提高自己的數學思維水平,獲得不一樣的數學智慧成長。
為此,在教學實踐中我從學生數學思維上存在的困難入手,分析學生在解題過程中遇到的困難,通過“慢”課堂幫助學生解決一個個數學思維上的困難。
一、“慢”課堂,慢在思維困惑處
培根說:數學是思維的體操。數學學習就是學生數學思維的訓練,教師在教學過程中要關注學生的數學思維,尤其是學生在數學思考中遇到了困惑時,應通過適當的回憶、鋪墊等方式,幫助他們順利地獲得新知識。
如某次我在教學蘇教版五年級下冊第三單元中“能被3整除的數的特征”一課時,學生通過預習知道了能被3整除的數的特征與能被2、5整除的數的特征不同,需要各個數位上的數相加的和是3的倍數。對于這個結論,很多學生只知結論,不知道為什么會出現這樣的結論。于是,我在課堂上讓學生展開了討論和研究。
生1:我用舉例法,比如22除以3,三七二十一,那么余下來的1在個位上。
生2:我舉例了三位數,比如157除以3,百位上的100除以3余下1,十位上和個位上合起來是“57”正好能被3整除,所以我們就知道了這個數不能被3整除。
生3:我舉例了四位數,比如1237除以3,千位和百位合起來是“1200”正好能被3整除,十位和個位合起來是“37”,除以3余數是1,所以這個數不能被3整除。
生4:我也通過舉例發現了能被3整除的數不僅與個位上的數有關,還與其他數位上的數有關。
師:大家真會動腦筋,現在我們體會到了為什么能被3整除的數需要各個數位上的數相加了。
在這個教學案例中,我通過放慢課堂的節奏,讓學生知道了能被3整除的數的結論,還知道了為什么會有這樣的結論。
二、“慢”課堂,慢在思維錯誤處
學生在數學學習中犯錯誤,既是他們在學習過程中的必經過程,又是教師研究學生思維的最佳著眼點。如我在教學蘇教版五年級上冊第二單元“平行四邊形的面積”一課時,學生在推導平行四邊形面積公式時出現了多種答案,如鄰邊×鄰邊、(鄰邊+鄰邊)×2、底×高等。
師:同學們,通過我們自己對平行四邊形面積的研究,出現了這3種答案,你支持哪一種,哪種你認為肯定是不對的,為什么?
甲洛洛主意已定,便右手提著斧頭,左手拿著手電筒,躡手躡腳地往倉庫走去。斧頭前幾天砍柴時磨過,手電筒剛換了新電池。
生1:我覺得(鄰邊+鄰邊)×2肯定是不對的,因為這是計算平行四邊形的周長公式。
生2:我覺得鄰邊×鄰邊這種方法也是不對的,因為剛才我用數格子的方法算出這個平行四邊形的面積是28平方厘米,而鄰邊×鄰邊算出來的答案是35平方厘米。
師:那大家都支持底×高這種方法,有誰能說說這種方法為什么是正確的?
生:我們可以把平行四邊形分割成長方形,長方形的長就是平行四邊形中的底,長方形的寬就是平行四邊形的高,因為長方形的面積是長乘寬,所以平行四邊形的面積就是底乘高了。
在這個教學案例中,我從學生的錯誤入手,在學生的錯誤之處開展深入的討論和交流,不僅糾正了學生的錯誤思維,還理清了為什么“底×高”是正確的。
三、“慢”課堂,慢在思維生長處
皮亞杰曾經說過:兒童的思維是從動作開始,切斷動作與思維的聯系,思維就得不到發展。由此可見,在學生數學思維的生長點上,教師要舍得花時間,讓學生通過直觀的動手操作,幫助他們理解數學知識,獲得思維的生長。
如我在教學蘇教版五年級上冊綜合與實踐活動“釘子板上的多邊形”一課時,學生通過操作不僅算出了多邊形的面積,還發現了多邊形的面積與多邊形邊上的釘子的數量之間的關系。
師:同學們,下面多邊形的面積各是多少平方厘米呢?每個多邊形邊上的釘子各有多少枚?請你先數一數、算一算,把結果填入表中,再和同桌說一說你的新發現。
生:我的這張表格是這樣的:
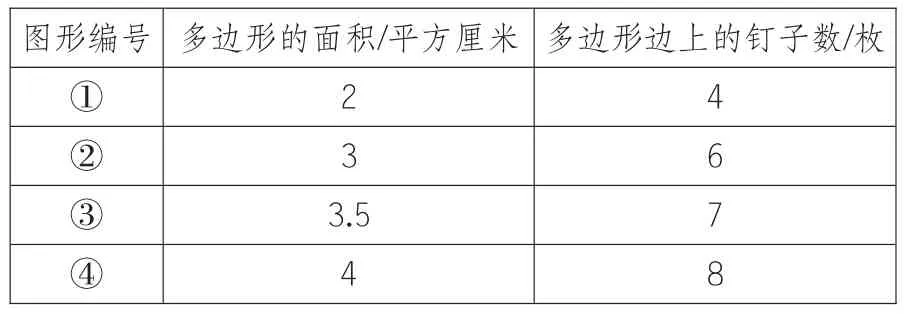
圖形編號多邊形的面積/平方厘米多邊形邊上的釘子數/枚①②③④2 3 3.5 4 4 6 7 8
師:大家的填法和他一樣嗎?
生:一樣。
師:很好,現在我們觀察這張表格中的數據和多邊形,你發現了什么?
生1:我發現圖形內都只有1枚釘子。
生2:我發現這些多邊形邊上的釘子數越多,面積越大。
生3:我發現這些多邊形面積的平方厘米數是它們邊上釘子數的一半。
師:剛才我們遇到的多邊形內只有1枚釘子,如果用n表示多邊形邊上的釘子數,用S表示多邊形的面積,你能寫出n和S之間的數量關系嗎?
在這個教學案例中,我放慢教學速度,讓學生投入地觀察、操作和計算,發現了很多釘子板上的規律。同時,通過這樣的學習模式,為學生今后解決相似的題目提供了可操作的模型。
總之,學生掌握數學知識的速度有快有慢,教師要在教學過程中學會尊重學生的個性差異,在“慢”課堂中耐心等待和引導,留給他們經歷與思考的時間,期待他們數學知識的生根發芽。
[1]方葉強.慢教育,讓數學課堂更精彩[J].貴州教育,2012(22).
[2]陳雨華.小學數學需要“慢教”[J].小學教學參考,2012(32).?