高速列車車下設備對車體垂向振動影響規(guī)律研究

賀小龍，張立民，魯連濤

(西南交通大學 牽引動力國家重點實驗室，成都 610031)

高速列車車下設備對車體垂向振動影響規(guī)律研究

賀小龍，張立民，魯連濤

(西南交通大學 牽引動力國家重點實驗室，成都 610031)

車下設備因其質量較大，對車體的振動模態(tài)特性和車輛乘坐舒適性都有著重要影響。建立了9自由度的車體-設備剛柔耦合數(shù)學模型，獲得了車體中部、構架上方三個參考點的加速度頻率響應函數(shù)表達式，研究了車下設備對車輛垂向振動的影響規(guī)律。考慮了在幾何濾波效應、設備的安裝方式(剛性、彈性)、運行速度等因素作用下，車體的三個參考點在垂向彎曲頻率下的振動加速度響應特性，最后討論了設備的質量以及吊掛阻尼比對車體振動水平的影響。研究結果表明，設備彈性懸掛能有效降低車體振動水平，在速度低于150 km/h，幾何濾波效應對車輛的振動影響較大，在此速度范圍內(nèi)設備懸掛參數(shù)設計應該充分考慮幾何濾波效應的影響，合理的選擇設備質量和阻尼比能有效控制車體的振動。

車下設備；加速度頻響函數(shù)；幾何濾波效應；安裝方式

隨著車體輕量化技術在鐵路運輸行業(yè)的運用[1]，車體的質量越來越輕，彈性越來越強，在線路激擾下更容易引起車體彈性振動。近幾年，EMU(Electric Multiple Unit)模式開始在車輛制造業(yè)中普及，諸如牽引變壓器、牽引變流器、空氣壓縮機等設備安裝在車體底架下，這些設備質量從幾十千克到幾噸不等，有的甚至自帶激勵源，在一定程度上影響了車輛的振動水平[2]。眾所周知，為了降低噪聲和衰減振動，大多數(shù)設備都是采用彈性懸掛，目前已有大批學者對于設備彈性懸掛進行了研究[3-5]，在以往的研究成果中，研究車體設備的耦合振動關系僅僅停留在靜態(tài)，并未涉及車輛在運行條件下的振動規(guī)律[6]。對此，本文建立了車體-設備的9自由度的剛柔耦合數(shù)學模型，獲得了車體中部、構架上方三個參考點的加速度頻率響應函數(shù)表達式，研究了車下設備對高速列車車體垂向振動的影響規(guī)律。同時考慮幾何濾波效應、車輛不同運行速度、不同安裝方式(剛性、彈性) 等因素，研究了車體在垂向彎曲頻率處的振動變化規(guī)律，獲得了設備質量和安裝阻尼比對車體振動衰減特性。本文的研究結論可以為車下設備的安裝設計提供指導。

1 車輛-設備耦合動力學模型

車輛-設備耦合系統(tǒng)垂向動力學模型如圖1所示[7]。本文所研究的車輛系統(tǒng)包含一個車體，兩個構架，四個輪對以及一個車下設備。車輛運行速度為V，并且假設輪軌完全接觸。文中將車體考慮成歐拉-伯努利梁，且其具有均勻分布質量，梁的長度為L，ρ=Mc/L為車體單位長度的質量，μ為車體結構阻尼系數(shù)，EI為車體的抗彎剛度。

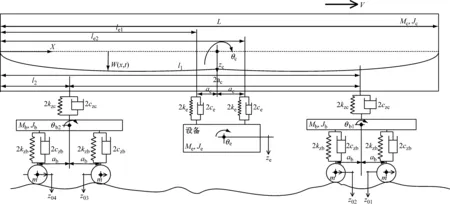
圖1 車輛設備耦合系統(tǒng)垂向動力學模型Fig.1 The vertical mechanical model of the vehicle-equipment coupling system

考慮車體的沉浮點頭和一階垂向彎曲運動，構架和設備的沉浮、點頭運動。其中車體的位移z(x,t)為車體的剛體振動與彈性彎曲振動的疊加

z(x,t)=zc(t)+(x-2/L)θc(t)+X2(x)T2(t)

(1)

其中梁的陣型函數(shù)求解過程見文獻[8-9]。本文中數(shù)值計算車輛參數(shù)如表1所示。

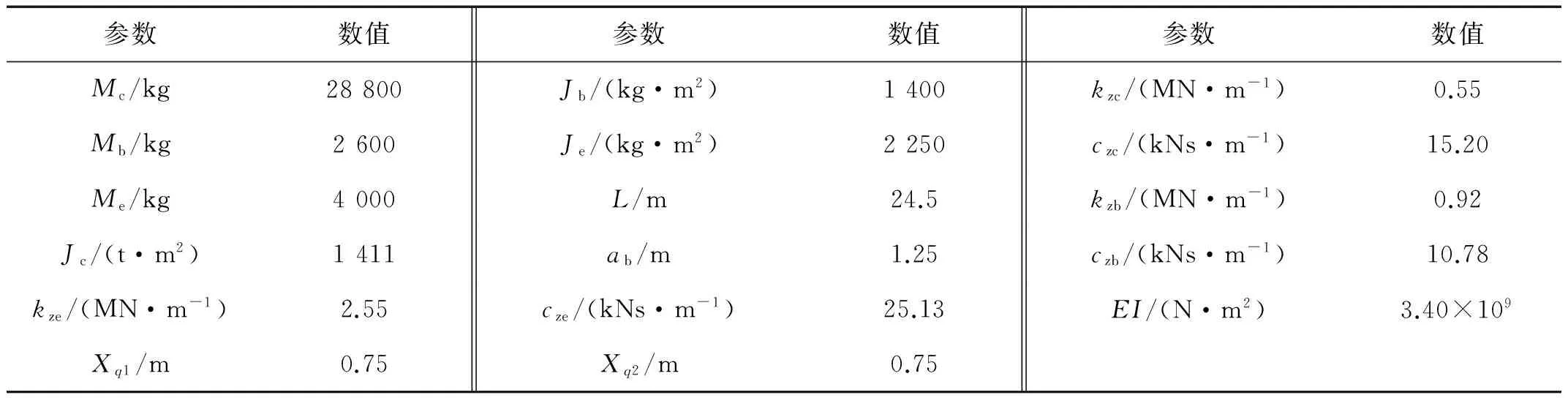
表1 車輛計算參數(shù)Tab.1 Vehicle calculate parameters

2 車輛-設備運動方程

圖1中，車體的運動方程為[10]

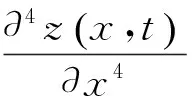
(2)

式中：δ(x)為狄克拉函數(shù)；li為2系支撐位置；lei為設備懸掛位置；Fzci為2系支撐力；Fzei為設備作用在車體上的力。

(3)

(4)

式中，2ae為設備懸掛位置。本文中只考慮車體的一階垂向彎曲模態(tài)，車體的沉浮、點頭、彎曲方程為

(5)

(6)

(7)

構架的沉浮、點頭運動

(8)

(9)

(10)

(11)

設備的沉浮、點頭運動

(12)

(13)

3 系統(tǒng)的頻響函數(shù)方程

對于2中車輛系統(tǒng)的動力學方程可以寫為[11]

(14)

式中，{y}=[zcθcT2zb1zb2θb1θb2zeθe]′為車輛系統(tǒng)的響應。則系統(tǒng)加速度響應頻響函數(shù)為

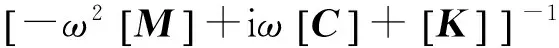
[[Dw]+iω[Ddw]]

(15)

車輛系統(tǒng)的響應為多輸入多輸出系統(tǒng)，考慮輪對激勵的時間滯后特性，可以將系統(tǒng)轉換為單輸入多輸出系統(tǒng)

(16)

式中，Z01(ω)為輪對1激勵函數(shù)；ti為其余輪對滯后時間，其中t1=2ab/V,t2=2ac/V,t3=2(ac+ab)/V。根據(jù)式(1)車體中部的加速度響應為

Ha(L/2,w)=ω2(Hzc(ω)+X2(L/2)HT2(ω))

(17)

轉向架上方(1、2位端)加速度響應為

Ha(l1,2,w)=ω2(Hzc(ω)±acHθc(ω)+

X2(L/2)HT2(ω))

(18)

4 車體數(shù)值計算結果分析

圖2為車體無設備、車體與設備剛性連接、車體與設備彈性連接時車體中部、車體轉向架上方的車體加速度頻響函數(shù)曲線。圖中，曲線在1.14 Hz處出現(xiàn)峰值，該頻率對應車體的沉浮模態(tài)，對于車體剛性模態(tài)這里不細討論。圖2中車體的垂彎頻率隨著設備的吊掛方式不同會發(fā)生改變：無車下設備時，車體的垂彎頻率為10.20 Hz；當設備剛性連接時，垂向彎曲頻率降至為9.38 Hz；當設備彈性連接時，車體-設備耦合系統(tǒng)垂彎頻率為7.78 Hz、11.40 Hz，這兩個頻率分別對應車體與設備振動同相、反相關系。車體吊掛設備后，車體在垂向彎曲頻率處的響應幅值也發(fā)生了變化：設備剛性連接導致車體中部振動降低，而構架上方振動增大；設備彈性連接后，相比另外兩種設備連接條件，振動響應在兩個彎曲頻率處有所降低，但車體中部振動差異不大，而在構架上方，低頻垂彎頻率下振動大于在高頻垂彎頻率處振動。

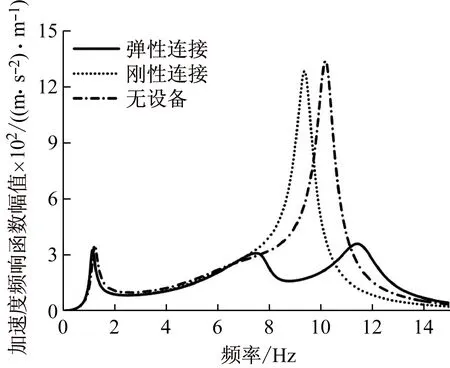
(a) 車體中部

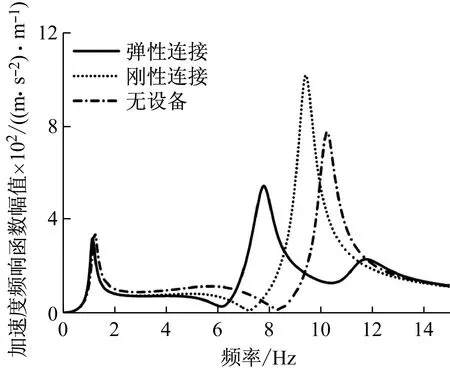
(b) 轉向架上方圖2 車體加速度頻響函數(shù)Fig.2 Acceleration frequency response function of car body

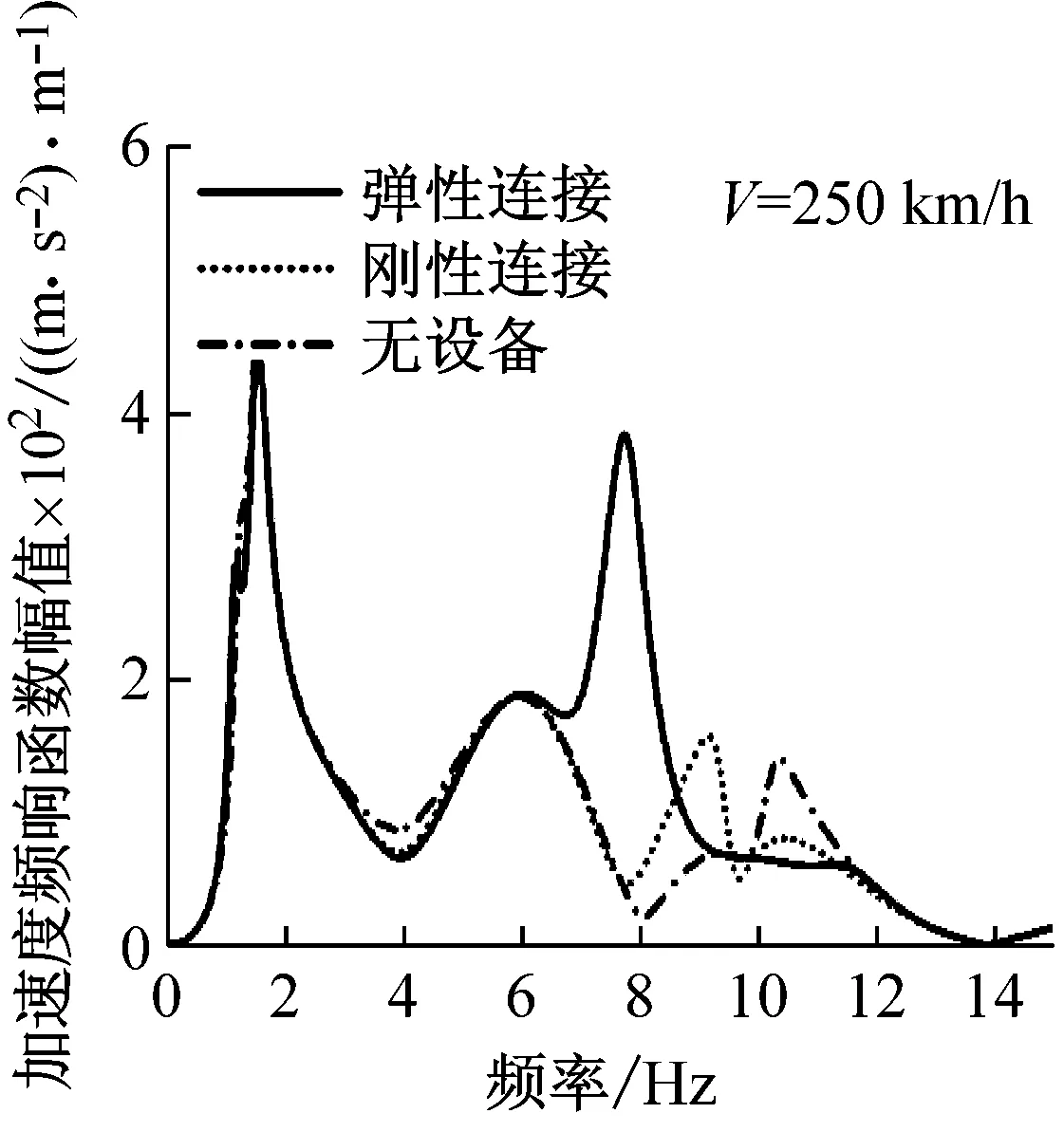
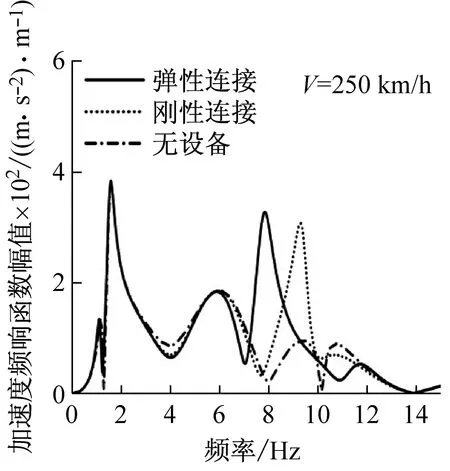
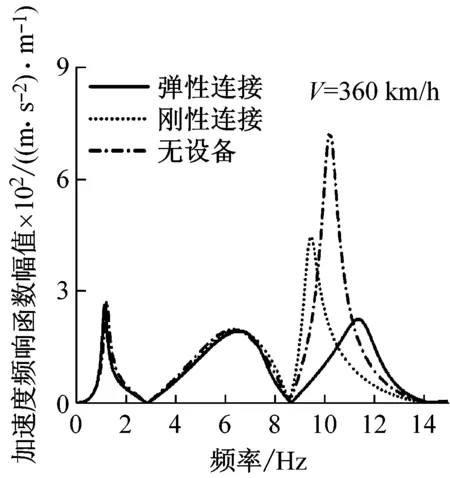
軌道車輛為多輪輸入，車輪軌道不平順垂向激勵存在時間滯后，其滯后常數(shù)由車輛定距，軸距和車輛行駛速度共同決定。在與懸掛系統(tǒng)共同作用下，會產(chǎn)生車體或者車體某階陣型對軌道某些不平順波長沒有響應的現(xiàn)象，這一現(xiàn)象稱為“幾何濾波效應”[12]，對于該效應作用原理這里不再贅述。圖3為車輛在時速250 km/h和360 km/h下車體中部和構架上方的加速度響應函數(shù)。本文中車輛幾何濾波頻率如表2所示。

由圖3可知，由于幾何濾波效應的緣故，車體參考點的響應函數(shù)中會出現(xiàn)一連串的極大值和極小值。圖3(a)中，響應為0的頻率點與表2中幾何濾波頻率吻合，設備三種連接工況下，車體的彎曲頻率(① 10.20 Hz、② 9.38 Hz、③ 7.78 Hz、11.40 Hz都避開了幾何濾波頻率，所以兩種速度下，車體中部在垂彎頻率處響應均不為0。

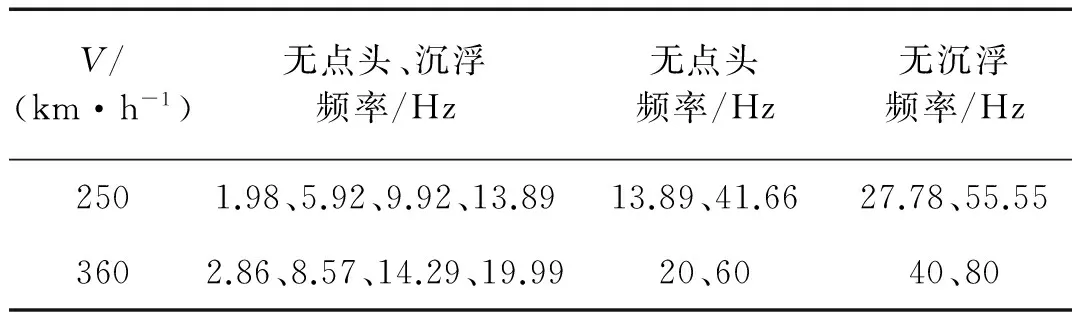
表2 車輛幾何濾波頻率Tab.2 The geometry filtering frequencies

圖3(b)、圖3(c)兩種速度下構架上方的車體響應，由圖可知，在幾何濾波頻率處，加速度響應不為0，這表明在車輛高速運行條件下，車體的一階彎曲彈性模態(tài)對于構架上方振動響應貢獻較大，即使幾何濾波效應存在，車體在濾波頻率點處，響應也不為0。

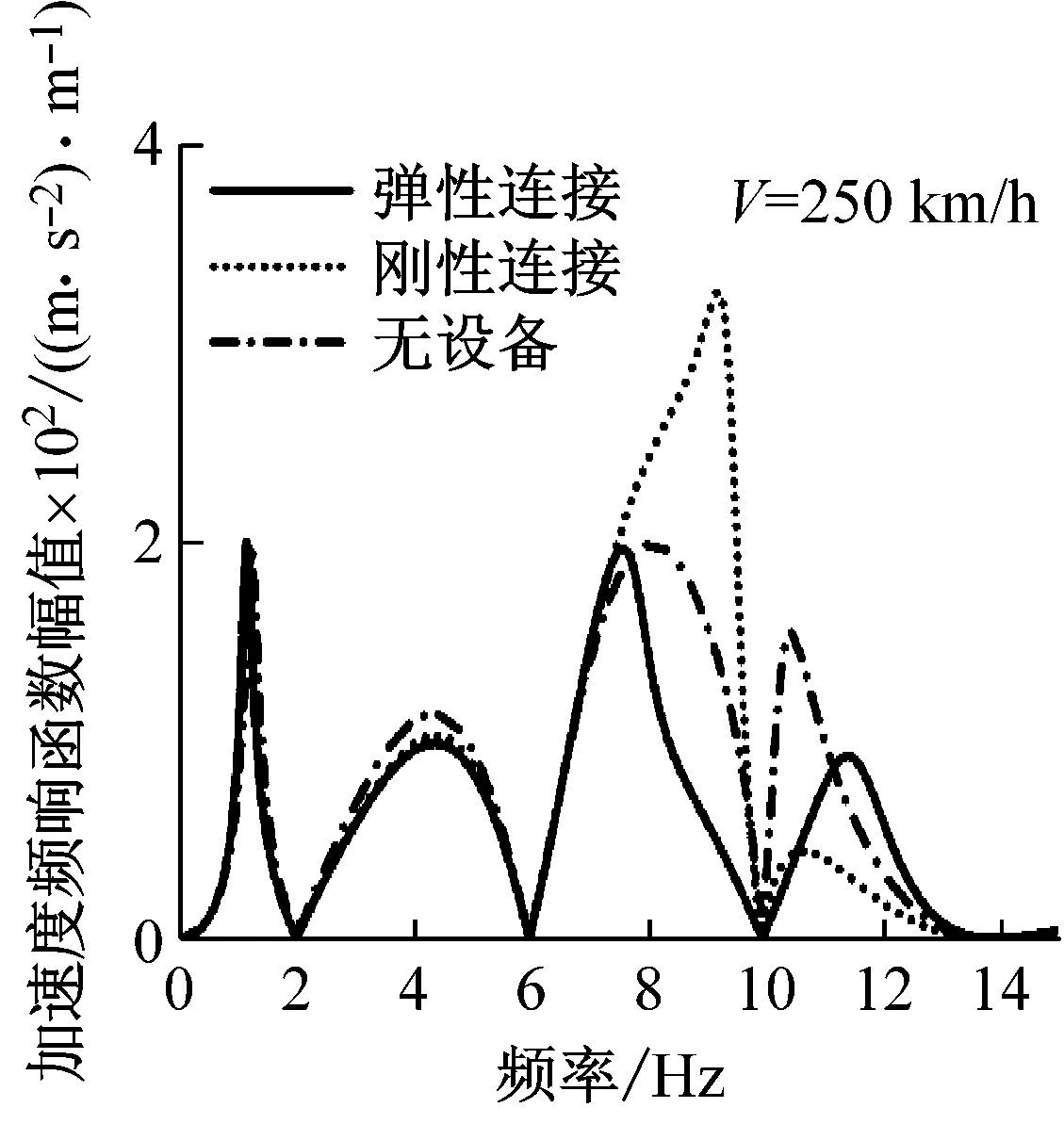
(a) 車體中部

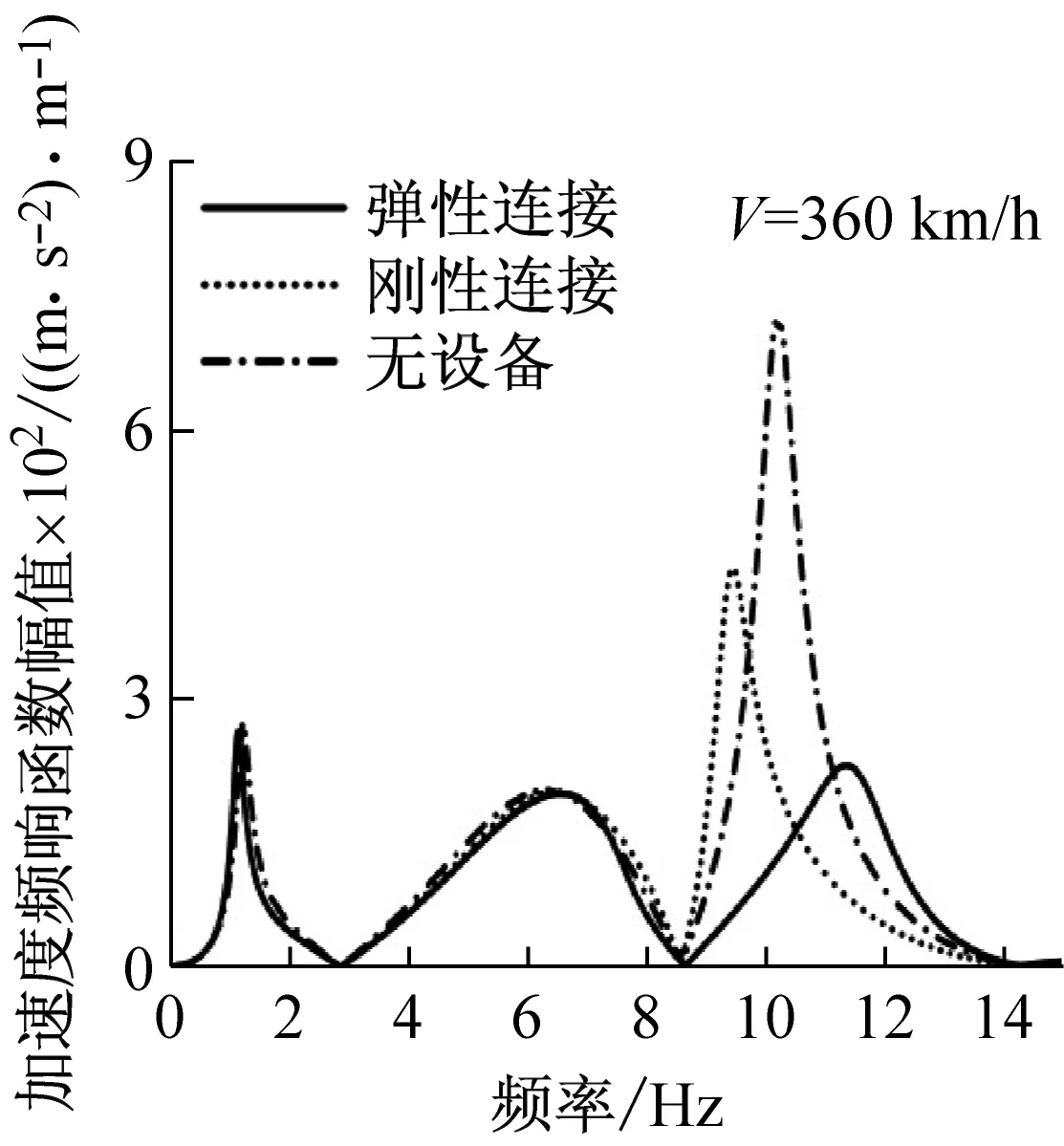
(b) 一位端構架上方

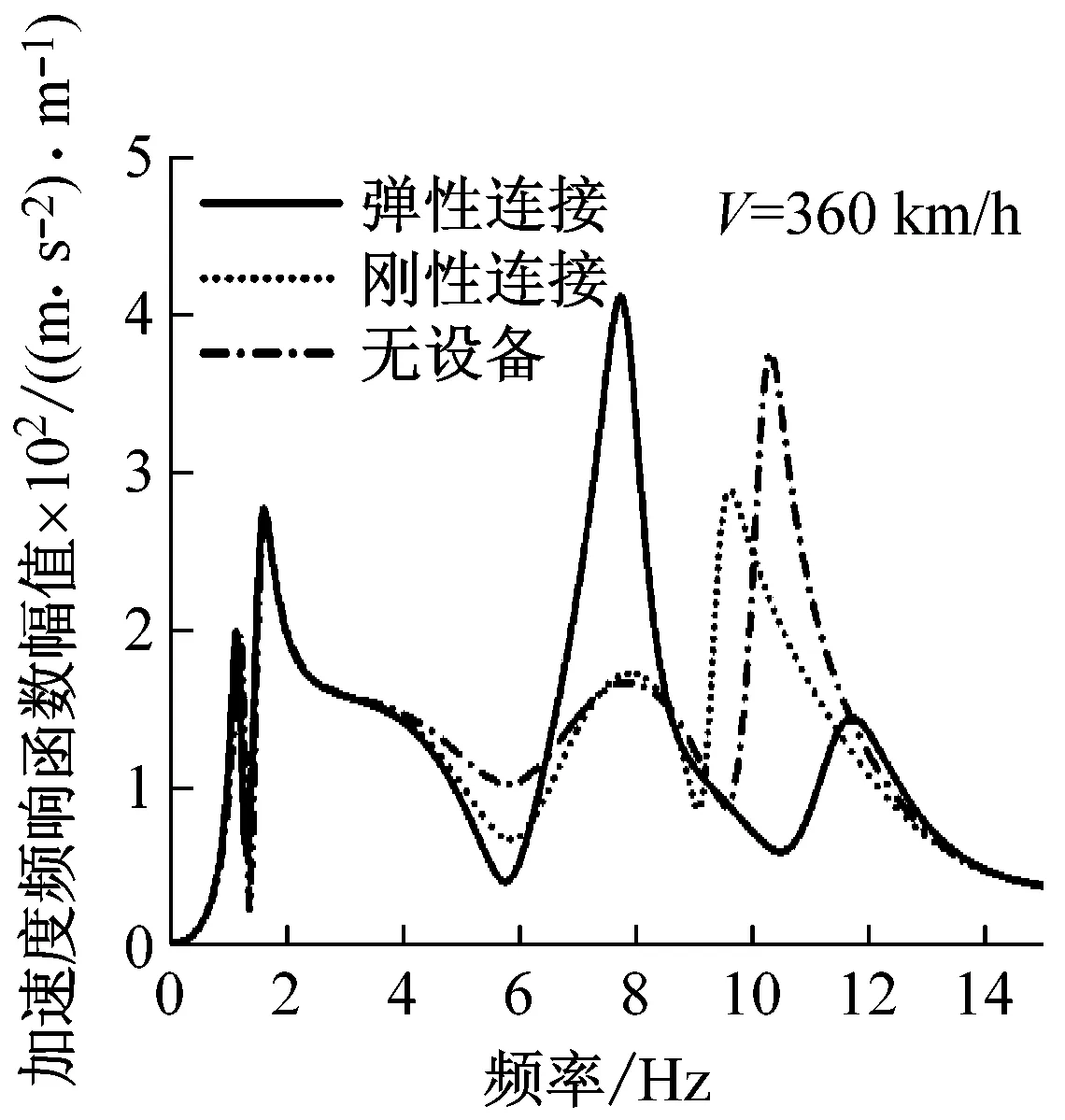
(c) 二位端構架上方圖3 車體加速度頻響函數(shù)Fig.3 Acceleration frequency response function of car body

圖3中，車速為250 km/h時，幾何濾波效應體現(xiàn)的更加明顯，對比兩種速度下車體響應特性可知幾何濾波效應對車速有選擇性：即速度越低，幾何濾波效應越明顯。設備三種連接方式下，車體在垂彎頻率處的振動幅度隨速度的變化程度較大。研究設備與車體的三種連接方式對于車體在彎曲固有頻率處振動的影響關系，必須考慮車輛的運行速度。例如：以無設備的車體振動程度為基準，設備剛性連接會導致在250 km/h時車體中部的振動增大，卻使得在360 km/h時車體中部振動減小；當設備彈性連接時，車體中部的振動強度在兩種速度下都減小。

幾何濾波效應作為速度、車輛定距、軸距的函數(shù)，車體在的垂彎頻率處的振動對速度具有一定的選擇性，這也解釋了圖中在特定速度下，車體的響應被削弱這一現(xiàn)象。因為在特定的速度下，幾何濾波頻率與車體垂向彎曲頻率一致，車體彈性振動對車體的振動的影響也得到衰減。圖4中，幾何濾波效應對車輛的行駛速度具有選擇性，在速度小于150 km/h的低速區(qū)間，該效應較為明顯，行駛速度越高，幾何濾波效應的影響越小。當無設備和設備剛性連接時，因車體彎曲振動引起的車體中部振動比轉向架上方振動大；當設備彈性連接時，在低階車體彎曲頻率時車體中部振動小于轉向架上方振動，在高階車體彎曲頻率時，情況恰恰相反。設備彈性懸掛后，車體在垂彎頻率處的振動明顯小于無設備和設備剛性連接工況下振動。

圖5研究了設備彈性懸掛下，速度對于三個參考點振動的影響，由圖可知隨著速度增加，參考點振動變化較大，圖中參考點的響應峰值對應車體的固有模態(tài)頻率：車體沉浮-1.14 Hz；車體點頭-1.52 Hz；車體垂向彎曲-7.78 Hz、11.40 Hz。速度為150 km/h時，因為幾何濾波效應的緣故，車體中部響應在固有頻率處未表現(xiàn)出峰值，而轉向架上方在車體高頻率彎曲振動處也未出現(xiàn)峰值。這說明速度為150 km/h時，幾何濾波效應會濾去車體固有頻率對車體中部振動的影響，也會濾去彎曲振動對轉向架上方振動的影響。之前討論過，速度高于150 km/h，幾何濾波效應就會削弱，時速為250 km/h、350 km/h，參考點振動在車體固有頻率處表現(xiàn)出明顯峰值，構架上方在低頻率彎曲頻率處振動大于高頻率彎曲振動頻率處的振動；速度為350 km/h下，車體中部振動在低頻彎曲頻率處并未出現(xiàn)峰值，峰值在250 km/h下出現(xiàn)。

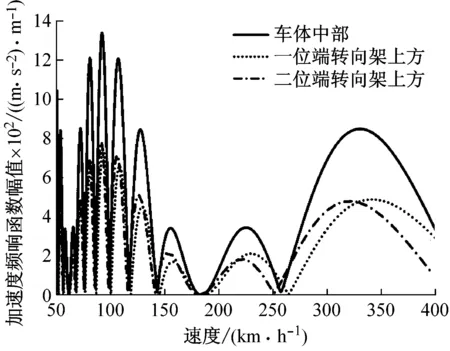
(a) 10.2 Hz-無設備

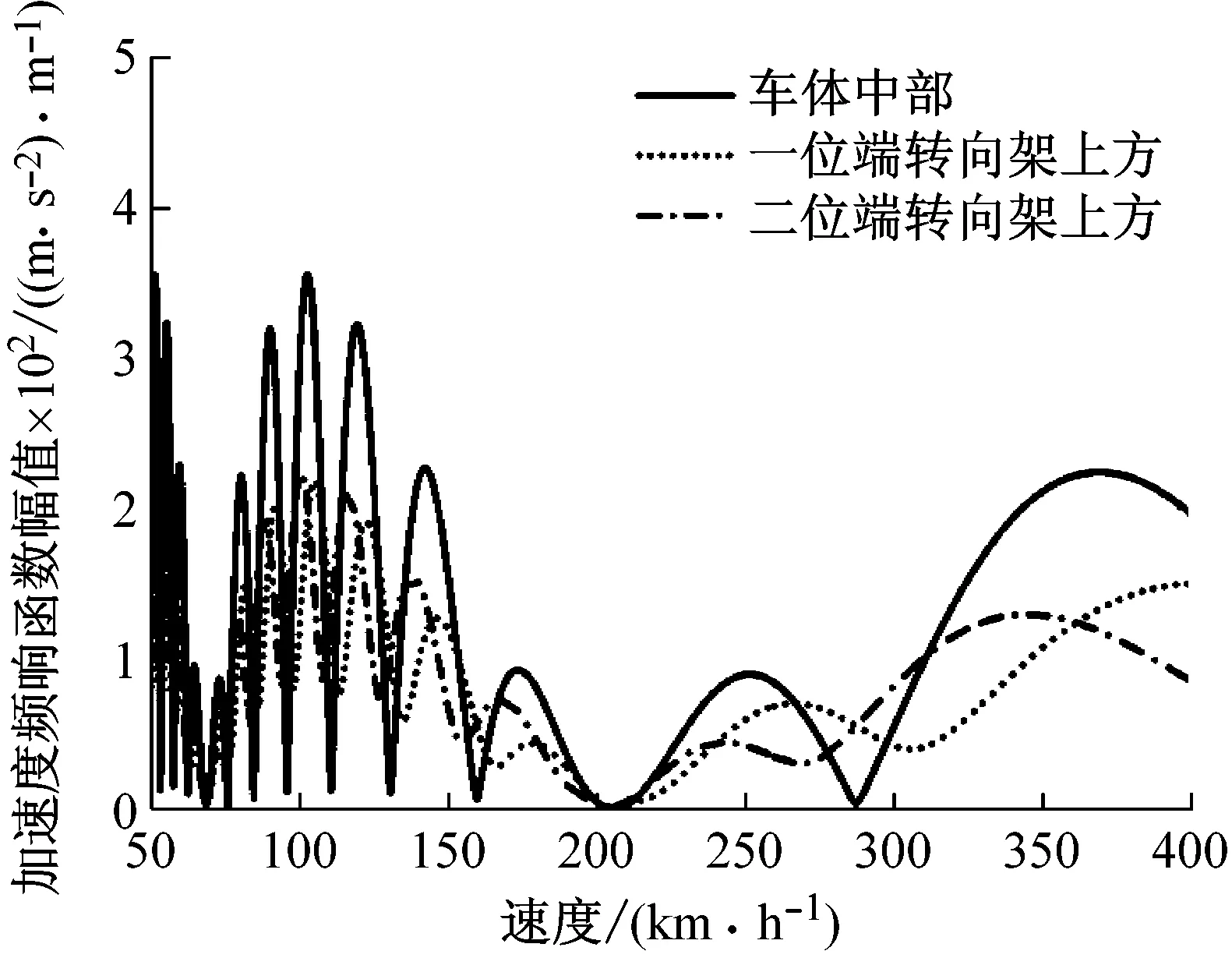
(b) 9.38 Hz-設備剛性連接

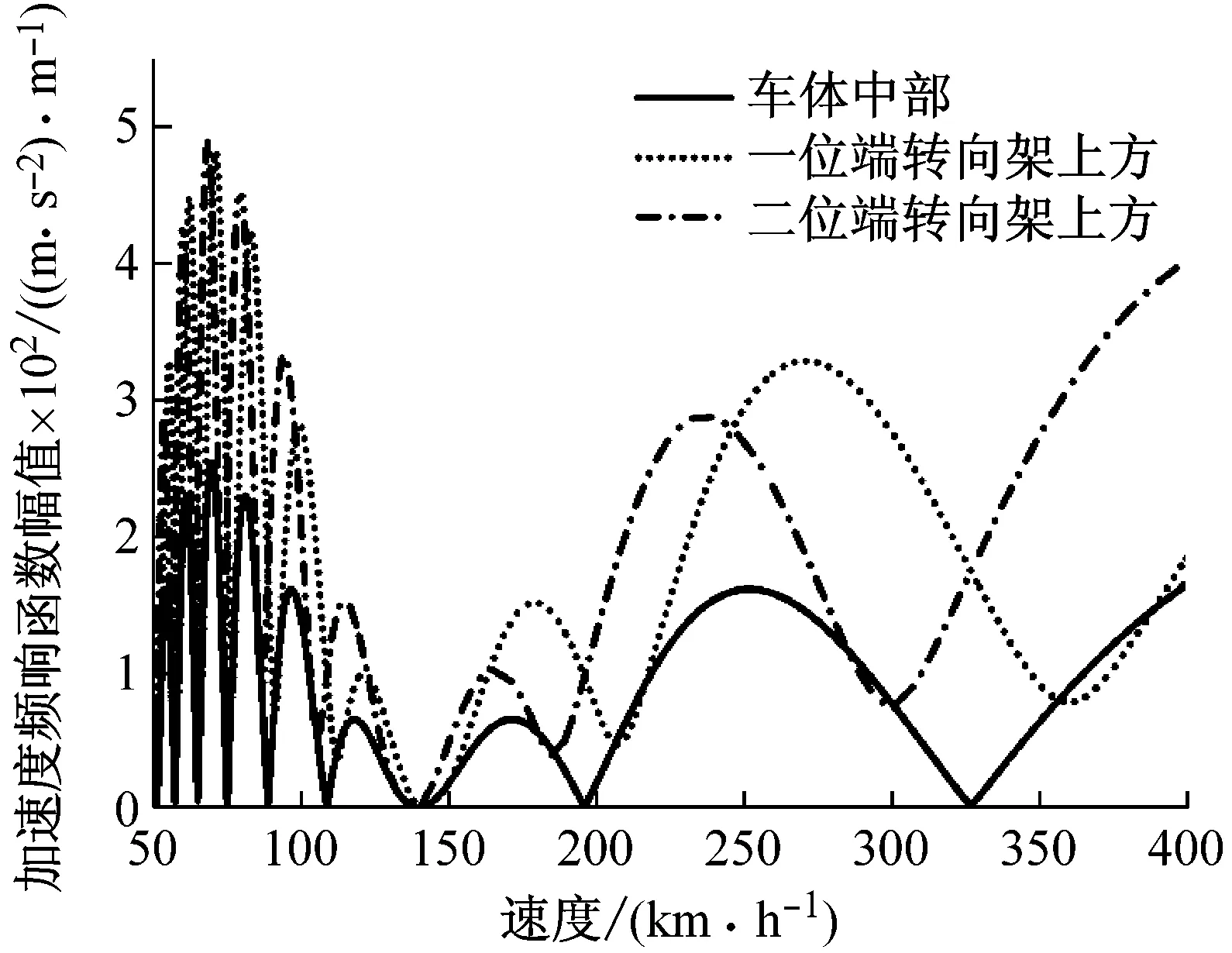
(c) 7.78 Hz

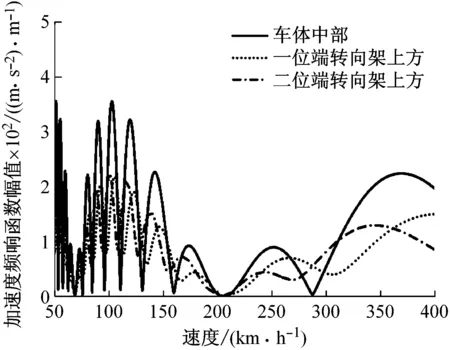
(d) 11.4 Hz-設備彈性連接圖4 彎曲頻率下車體加速度頻響函數(shù)Fig.4 Acceleration frequency response functionof car body at the bending frequencies

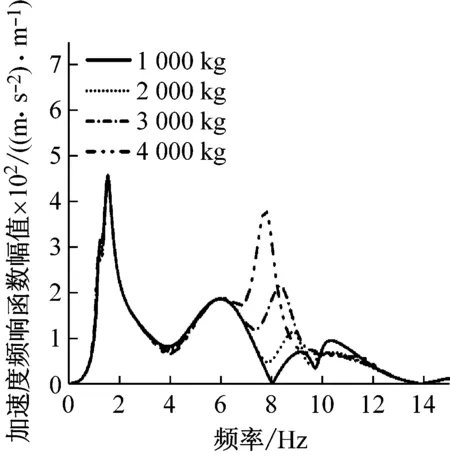
圖6討論了設備彈性懸掛下，車輛行駛速度為250 km/h時設備質量對車體加速度頻響函數(shù)的影響。如圖所示，設備質量的改變主要影響車體在垂彎頻率處的振動特性。在車體低階彎曲頻率處，設備質量的增加會導致車體中部和轉向架上方振動水平發(fā)生相同的變化。在車體高階彎曲頻率處，車體振動水平會隨著設備質量的增加而降低。圖中可以明顯看出，隨著設備質量的增加，車體兩階彎曲頻率的擴展范圍逐漸增大。

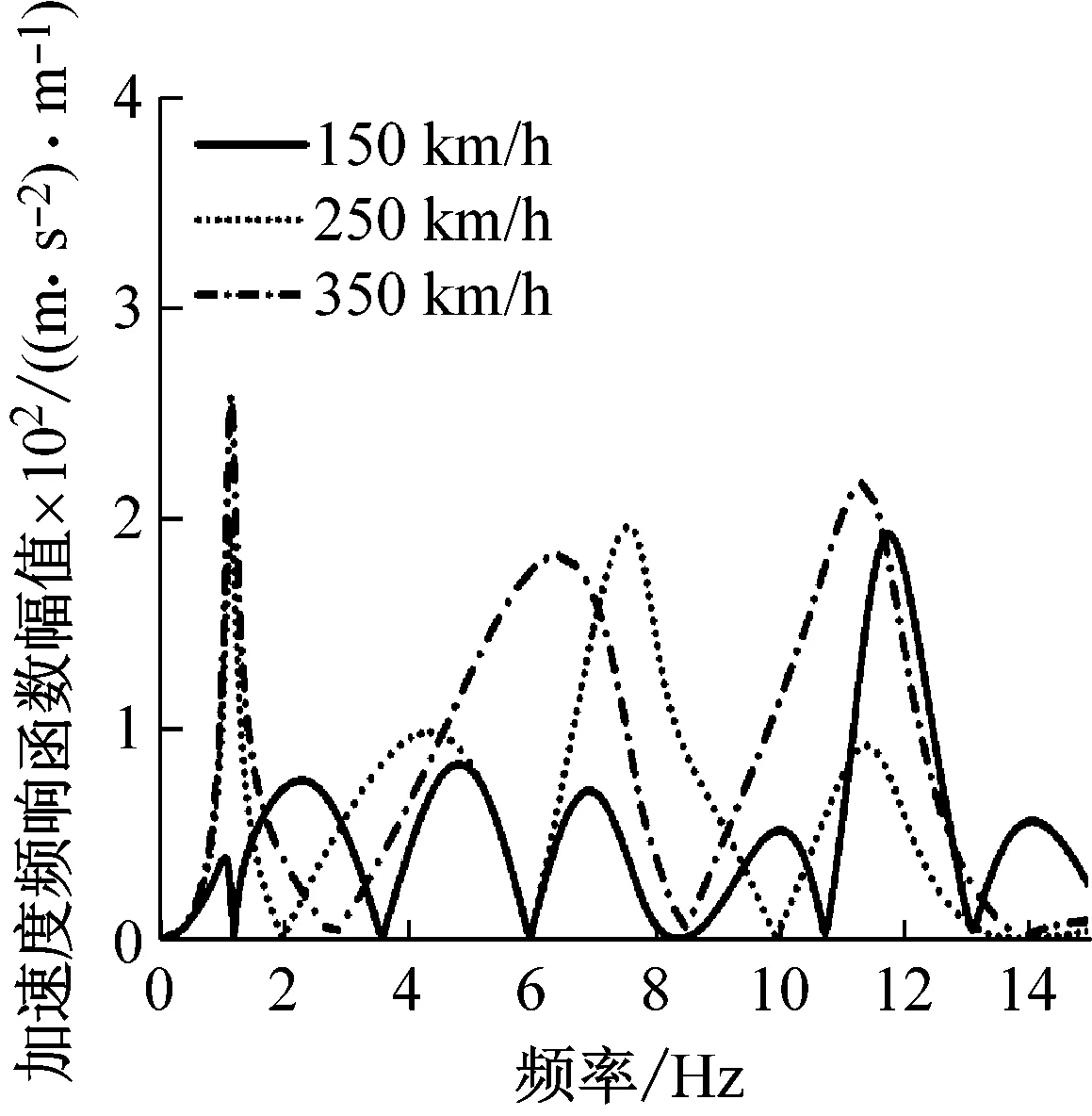
(a) 車體中部

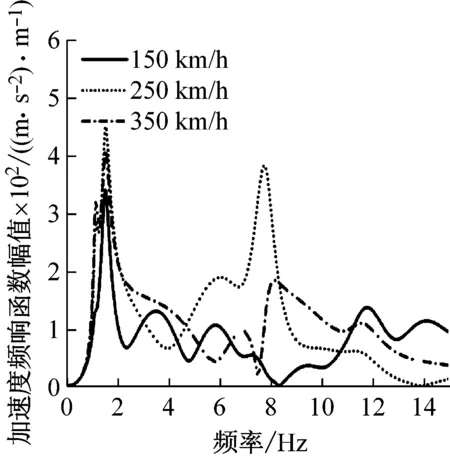
(b) 一位構架上方

(c) 二位構架上方圖5 速度對車體振動響應的影響Fig.5 The influence of velocity on the vehicle vibration

圖7研究了設備吊掛阻尼比對車體振動的影響。由圖7可知,隨著阻尼比的增大，在車體兩個彎曲頻率處，車體中部和兩位端轉向架上方振動水平逐漸降低。

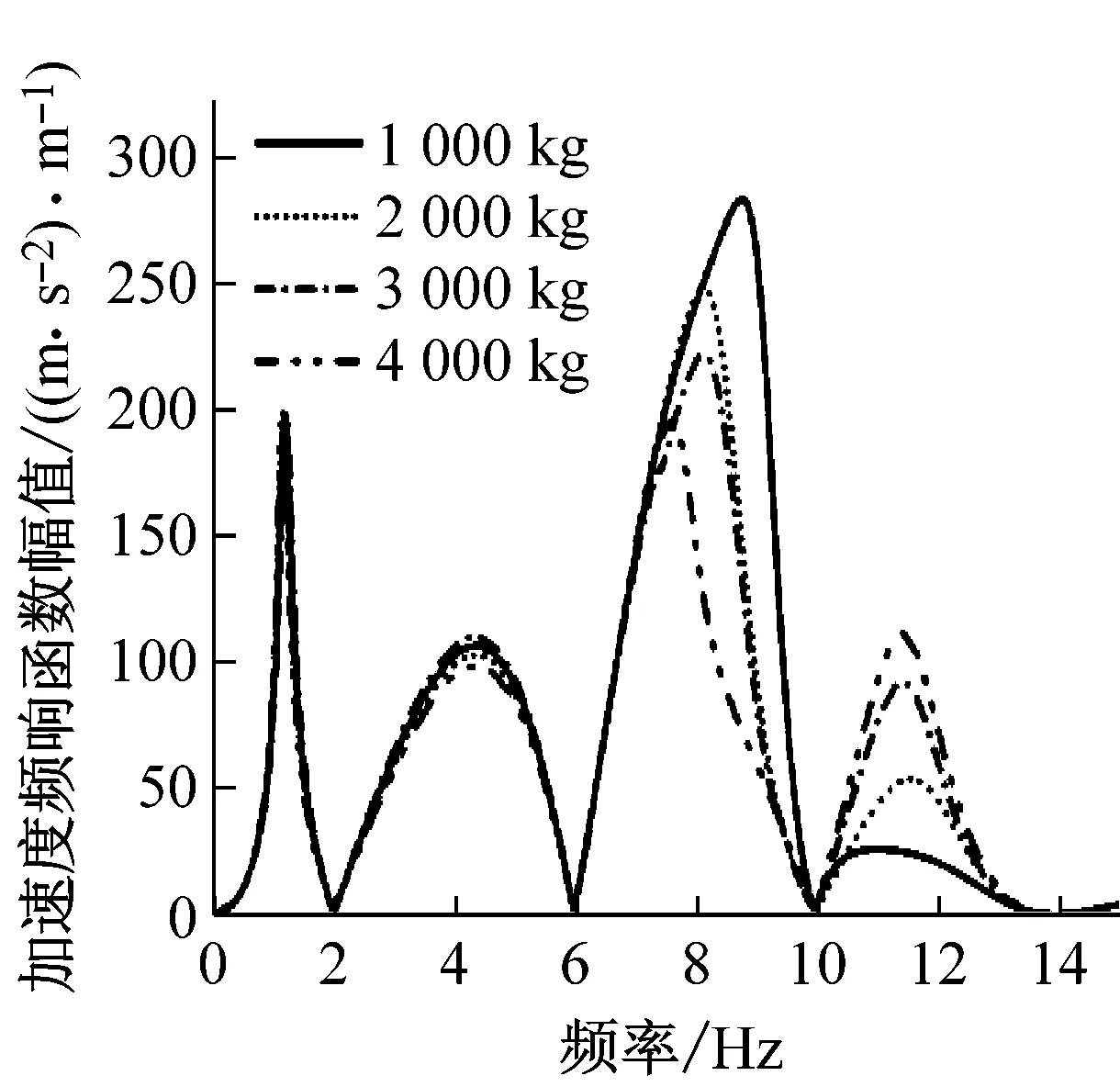
(a) 車體中部

(b) 一位構架上方

(c) 二位構架上方圖6 設備質量對車體響應的影響Fig.6 The effect of equipment mass on the vehicle vibration

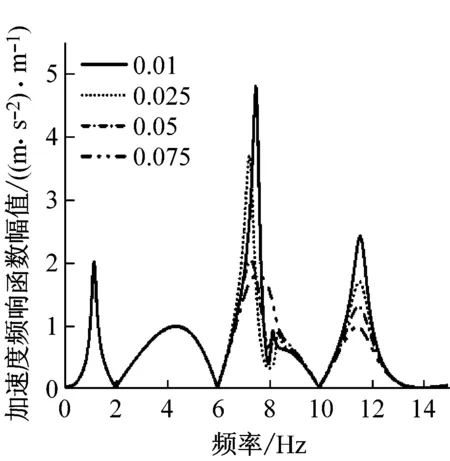
(a) 車體中部

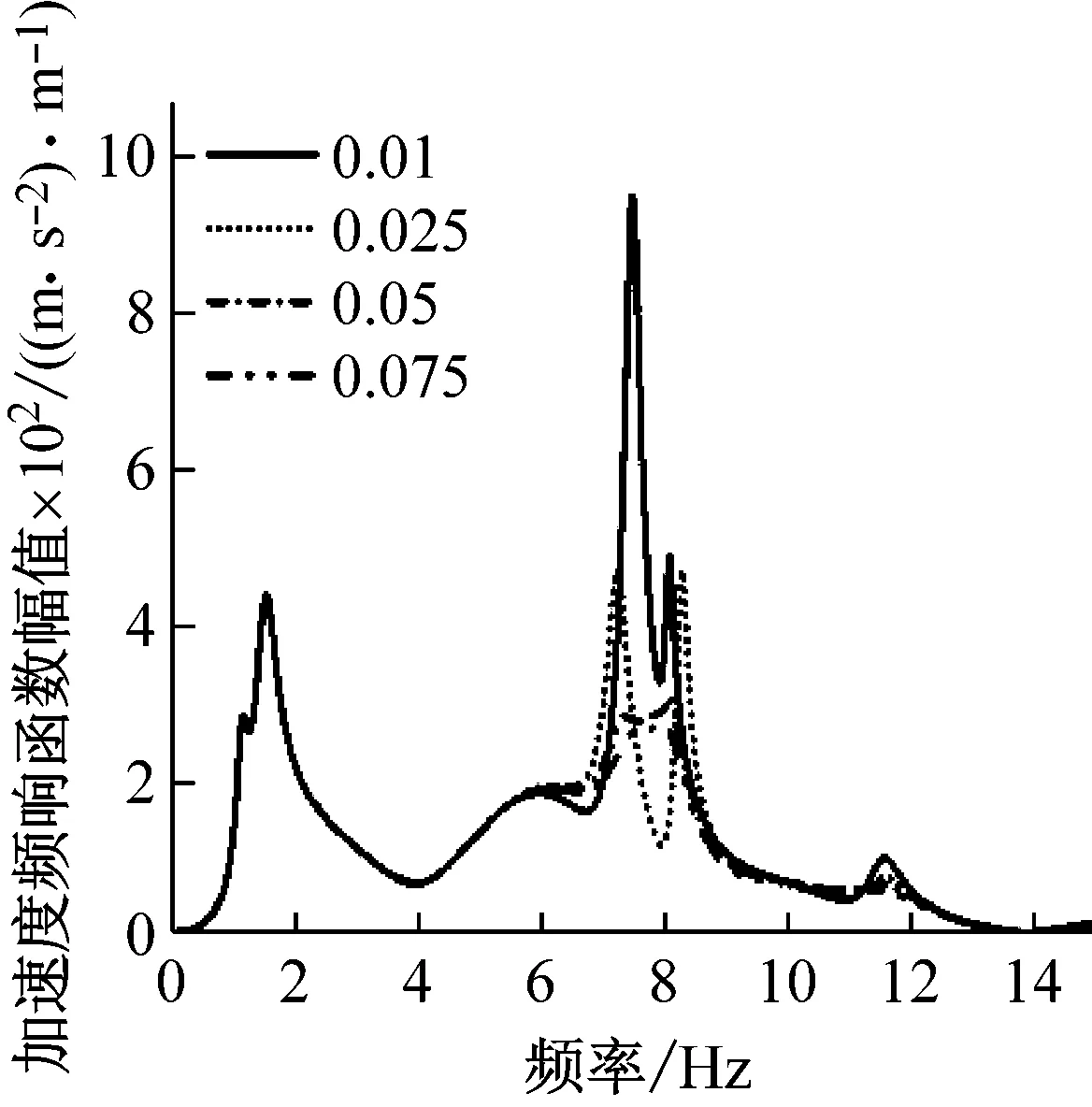
(b) 一位構架上方

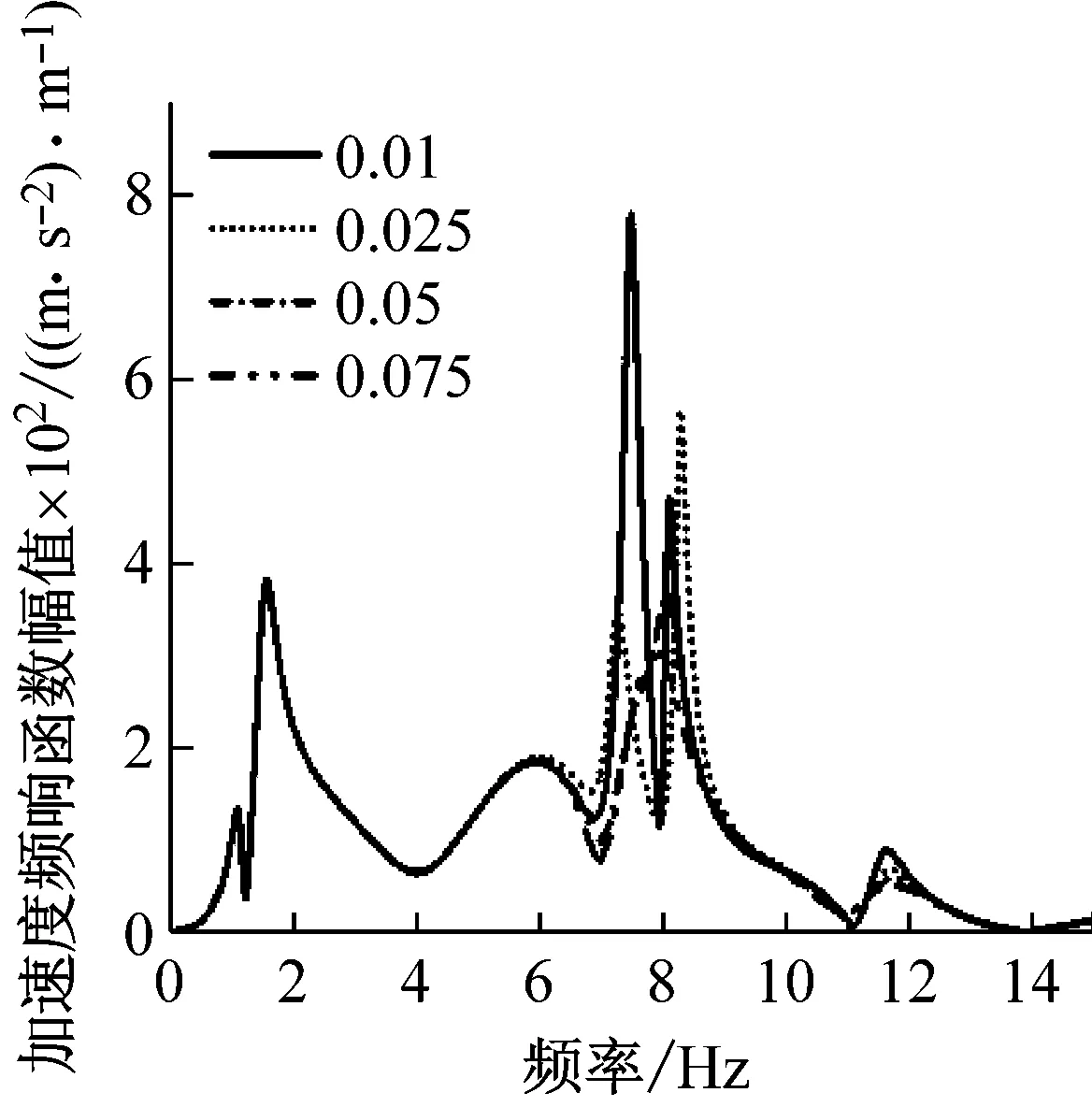
(c) 二位構架上方圖7 阻尼比對車體響應的影響Fig.7 The influence of damping ratio on the vehicle vibration

5 結 論

車下設備對高速列車垂向振動有著重要的影響，本文建立了車輛-設備耦合數(shù)學模型，基于車體參考點的加速度頻率響應函數(shù)對該影響進行了研究。其結論如下：

(1) 車體的垂向彎曲頻率會因為設備的安裝方式(剛性、彈性)不同發(fā)生改變，設備彈性安裝時，會出現(xiàn)兩個垂向彎曲頻率，他們分別對應設備與車體的同相振動和反相振動頻率。

(2) 幾何濾波效應作為速度、軸距、車輛定距的函數(shù)，特定車輛結構在不同速度下，幾何濾波效應對設備不同安裝方式(剛性、彈性)下車輛的動態(tài)行為影響不同，因此研究設備對車輛垂向振動的影響務必考慮速度的影響因素。

(3) 隨著彈性安裝設備質量的增加，在低階彎曲頻率處車體三個參考點的振動變化趨勢一致，而在高頻彎曲頻率處參考點的變化趨勢又不同。通過合理選擇合適的安裝阻尼比，車體在兩個彎曲頻率處的振動水平都能得到合理的衰減。

[1] 黃問盈,黃民.21世紀初鐵道高速列車特色[J]. 鐵道機車車輛,2009(2):23-30.

HUANG Wenying,HUANG Min.Distinct features of railway high speed train in early year of the 21th century[J].Railway Locomotive & CAR, 2009(2):23-30.

[2] 宮島,周勁松,孫文靜,等.下吊設備對高速列車彈性車體垂向運行平穩(wěn)性影響[J].中國工程機械學報,2011,9(4):404-409.

GONG Dao, ZHOU Jinsong, SUN Wenjing, et al. Impact of hanging equipments on vertical riding stability of elastic high-speed train bodies [J].Chinese Journal of Construction Mechinery, 2011,9(4):404-409.

[3] 羅光兵,曾京.車下設備的連接方式及懸掛參數(shù)匹配研究[J].現(xiàn)代制造工程,2013(5):1-6.

LUO Guangbing,ZENG Jing.Study on carbody flexible vibration with considering under frame suspended equipment [J].Modern Manufacturing Engineering, 2013(5):1-6.

[4] 吳會超,鄔平波,曾京,等. 車下設備對車體振動的影響[J]. 交通運輸工程學報,2012，12(5):50-56.

WU Huichao,WU Pingbo,ZENG Jing,et al.Influence of equipment under car on carbody vibration [J].Journal of Traffic and Transportation Engineering, 2012,12(5):50-56.

[5] 吳會超,鄔平波,吳娜,等. 車下設備懸掛參數(shù)與車體結構之間匹配關系研究[J]. 振動與沖擊,2013,32(3):124-128.

WU Huichao, WU Pingbo, WU Na,et al.Matching relations between equipment suspension parameter and a car body structure[J].Journal of Vibration and Shock, 2013,32(3):124-128.

[6] 周勁松,孫文靜,宮島. 鐵道車輛幾何濾波現(xiàn)象及彈性車體共振分析[J]. 同濟大學學報(自然科學版),2009,37(12):1653-1657.

ZHOU Jinsong,SUN Wenjing,GONG Dao.Analysis on geometric filtering phenomenon and flexible car body resonant vibration of railway vehicle [J].Journalof Tongji University (Natural Science), 2009, 37(12):1653-1657.

[7] DUMITRIU M.Influence of the vertical suspension on the vibration behavior in the railway vehicles [J].Annals of the University of Petrolane, Mechanical Engineering, 2011(13): 35-50.

[8] DUMITRIU M.On the critical points of vertical vibration in a railway vehicle [J].Archive of Mechanical Engineering, 2016,16(4):609-625.

[9] ZHOU J,GOODALL R,REN L,et al.Influences of car body vertical flexibility on ride quality of passenger railway vehicles[J].Journal of Rail and Rapid Transit, 2009,223(5): 461-471.

[10] GONG Dao, SUN Wenjing, ZHOU Jinsong, et al.Analysis on the vertical coupled vibration between bogies and metro car body[J].Procedia Engineering, 2011(16):825-831.

[11] DUMITRIU M.Evaluation of the comfort index in railway vehicles depending on the vertical suspension features[J].International Journal of Engineering，2013，4(11):23-32.

[12] GONG Dao, ZHOU Jinsong, SUN Wenjing.On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber [J].Journal of Vibration and Control, 2012,19(5): 649-657.

Effectsofsuspendedequipmentsontheverticalvibrationofhigh-speedvehicle

HE Xiaolong, ZHANG Limin, LU Liantao

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

The big-mass equipment under the car has an important influence on the vehicle’s modal characteristics and ride comfort. The mathematical model of a 9-freedom rigid-elastic coupling vehicle system was established. And the effect of the equipment on the vertical vibration of the vehicle was investigated by analysing the acceleration FRFs at some reference points. The vehicle acceleration frequency response characteristics at certain vertical bending vibration frequencies were obtained considering the factors of geometric filtering effect, equipment installation type (rigid, flexible), and running speed.Finally, the influences of equipment mass and damping ratio on the vehicle body vibration level were studied. The results show that: the elastic suspension can effectively reduce the vibration of the car body. The geometric filtering effect is quite obvious when the speed is lower than 150 km/h. It is necessary to take the geometric filtering effect into account to reduce the vibration when the equipment mass and damping ratio are chosen reasonably.

suspended equipment; acceleration frequency response function; geometric filtering effect; installation method

U27

A

10.13465/j.cnki.jvs.2017.19.007

2016-06-23 修改稿收到日期：2016-07-30

賀小龍 男，博士生，1989年12月生

張立民 男，博士，研究員，1961年10月生