超深礦井提升機多層纏繞鋼絲繩圈間過渡對鋼絲繩動張力的影響研究

李曉光，龔憲生，吳水源，羅宇馳

(1.重慶大學 機械傳動國家重點實驗室,重慶 400044；2.重慶大學 機械工程學院,重慶 400044)

超深礦井提升機多層纏繞鋼絲繩圈間過渡對鋼絲繩動張力的影響研究

李曉光1,2，龔憲生1,2，吳水源1,2，羅宇馳1,2

(1.重慶大學 機械傳動國家重點實驗室,重慶 400044；2.重慶大學 機械工程學院,重慶 400044)

針對超深礦井提升機多層纏繞，研究多層纏繞鋼絲繩圈間過渡時的加速度變化，運用提升鋼絲繩的動張力微分方程和MATLAB中的Simulink模塊，建立對稱及非對稱雙折線過渡繩槽下多層纏繞鋼絲繩的動張力仿真模型并對仿真結果進行分析比較。結果表明，多層纏繞鋼絲繩在圈間過渡時產生的加速度變化會對鋼絲繩的動張力產生明顯的影響，采用對稱式折線繩槽進行圈間過渡時的動張力大于非對稱折線繩槽，在提升階段的后期此現象尤為明顯。這些結果對超深井提升系統多層纏繞研究有重要的參考價值。

多層纏繞；圈間過渡；雙折線過渡繩槽；動張力

隨著經濟社會的發展，我國對于礦產資源的需求日益增加，但是淺層礦產資源的逐漸耗盡已經嚴重制約我國經濟的快速發展，深部資源的開采利用已經成為我國的重大發展戰略。目前，我國僅對800 m以內的淺層礦井提升設備形成了較為完善的產品設計理論、提升檢測和安全標準，但現有傳統的單繩纏繞式提升機與多繩摩擦式提升機已不能滿足超深井提升(井深>1 500 m)的要求[1]，采用雙折線過渡繩槽的多鋼絲繩多層纏繞的多點提升組合拓撲結構有望成為超深井提升裝備的有效型式，其結構及繩槽形式如圖1所示。雙折線過渡繩槽分為對稱雙折線過渡繩槽和非對稱雙折線過渡繩槽，對稱雙折線過渡繩槽的兩個折線過渡區的圓心角間隔Ψ為180°；而非對稱雙折線過渡繩槽的布置形式為其中一個折線過渡區在原對稱的位置上偏置30°，即圓心角間隔Ψ為150°。目前，超深礦井提升系統鋼絲繩纏繞過程中的層間、圈間過渡行為、運行過程中動載荷的產生、傳播、消退機制等復雜動力學行為尚不明確，這已成為超深井提升設備研究過程中必須克服的科學技術難題。針對多層纏繞在圈間過渡時的速度變化及其對鋼絲繩動張力產生的影響進行研究，以期對超深井提升設備的設計和研發提供理論參考。

(a) 多繩多層纏繞式提升機

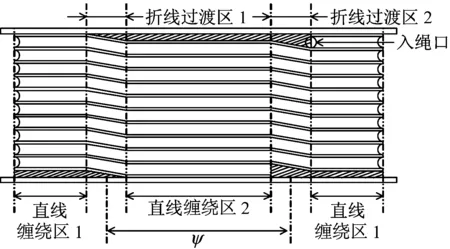
(b) 提升機卷筒繩槽展開圖圖1 多繩多層纏繞提升機及其繩槽Fig.1 Multi rope and multi-layer winding hoist and its groove

1 提升鋼絲繩的數學模型

提升鋼絲繩是一種柔性體，在提升過程中提升鋼絲繩由于受到加速度以及提升高度變化引起的提升質量變化等外部作用的影響，會產生振幅和頻率不斷變化的振動，鋼絲繩的振動會對于鋼絲繩的動張力有明顯的影響。

如圖2所示，提升機天輪左側的懸垂段鋼絲繩長度是隨時變化的，在天輪左側與鋼絲繩的切點處建立坐標系并采用采用瑞利法對提升鋼絲繩進行處理，即鋼絲繩質量的1/3加到終端質量上，當提升鋼絲繩按照圖3所示的三段圖運動規律進行提升運動時，鋼絲繩在加速、勻速和減速三個階段提升過程中動張力微分方程分別為[2]

2a1·F′)/L1(t)

(1)

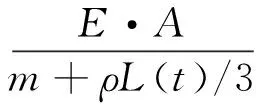
(2)

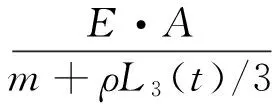
2[v-a2(t-t2)]·F′)/L3(t)

(3)

式中：F為鋼絲繩的動張力；a1、a2為提升過程中的加、減速度;E為鋼絲繩的楊氏彈性模量；A為鋼絲繩的橫截面面積;m為鋼絲繩提升的重物質量；ν為提升機勻速提升階段的速度；t1、t2為鋼絲繩加速和勻速階段結束的時間；Ln(t)為各提升階段鋼絲繩的繩長；ρ為鋼絲繩單位長度質量。

圖2 提升鋼絲繩運行示意圖Fig.2 Sketch diagram of the operation of hoist rope

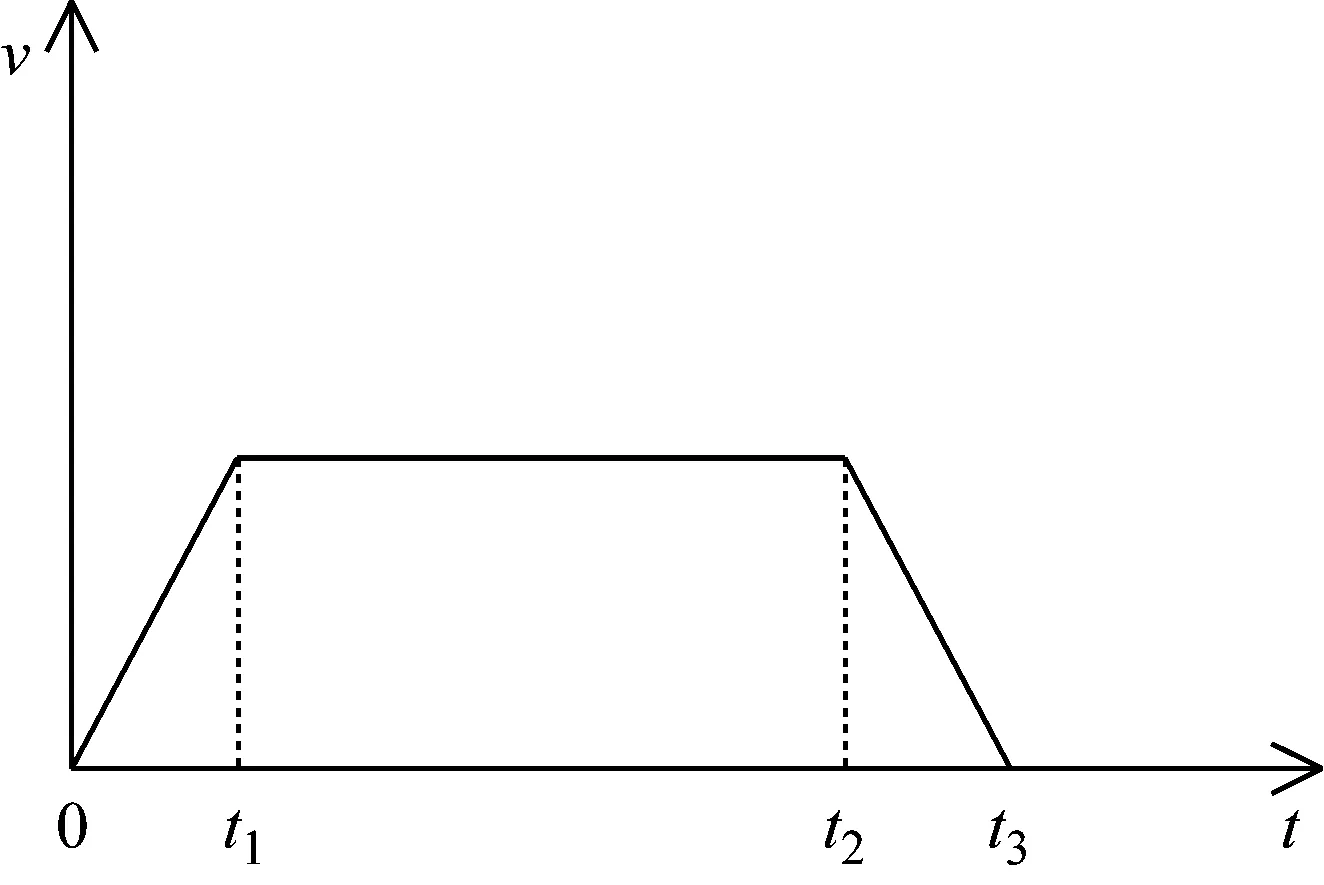
圖3 提升速度三段圖Fig.3 Hoisting speed of the wire rope

以中信重工提供的試驗臺數據為依據，提升機試驗平臺的鋼絲繩總繩長為46 m，有效提升距離為43 m，加速及減速提升階段的加速度值為±0.72 m/s2，勻速提升階段速度為1.8 m/s，由此計算后可知，加速、勻速和減速階段的結束時間分別為2.5 s、24 s和26.5 s，鋼絲繩繩長Ln(t)在三個提升階段內的變化為

L1(t)=L-(at2)/2

(4)

(5)

[v·(t-t2)-a(t-t2)2/2]

(6)

式中：t為提升時間；L為鋼絲繩總長。

將提升鋼絲繩相關參數代入式(4)～式(5)可得

L1(t)=46-0.36·t2(0≤t≤2.5)

(7)

L2(t)=48.25-1.8·t(2.5≤t≤24)

(8)

L3(t)=255.61-19.08·t+0.36·t2

(24≤t≤26.5)

(9)

鋼絲繩在多層纏繞時，上層鋼絲繩會纏繞在下層兩根鋼絲繩形成的繩槽內，由于上下層鋼絲繩的排繩方向不同，上層的一根鋼絲繩圈橫跨兩個相鄰的繩槽，從而產生纏繞過程中的圈間過渡。鋼絲繩在圈間過渡時，由于纏繞半徑的變化會引起鋼絲繩提升速度的變化，盡管速度變化不大，但是由于過渡時間也比較短，所以會有比較大的加速度變化，因此會引起鋼絲繩動張力的變化。依據所參照的提升機試驗平臺，繩槽纏繞寬度為170 mm，繩槽間隙為0.7 mm，纏繞層數為三層，第一層纏繞3圈，第二層纏滿12圈，第三層纏繞2圈。由于加速提升階段較短，此階段內的鋼絲繩尚處于第一層纏繞，此時圈間過渡并不會引起纏繞半徑的變化，鋼絲繩在第二層纏繞時才會受到圈間過渡加速度的影響。圈間過渡開始出現加速度變化的時間為5.4 s，此時已纏繞的繩長為10.9 m。

由于加速提升階段不受圈間過渡加速度變化的影響，因此本文主要分析圈間過渡加速度對勻速和減速提升階段的動張力影響。鋼絲繩圈間過渡時的纏繞半徑變化如圖4所示。

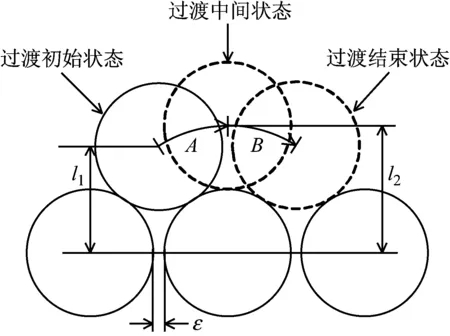
圖4 圈間過渡時的纏繞半徑變化Fig.4 The variation of the winding radius during the transition between the circles

由于圈間過渡時鋼絲繩纏繞產生的半徑差相對卷筒直徑要小得多，且過渡區很小，若按照幾何特征計算將變得非常繁瑣且計算的結果差別不大，為了計算方便，只考慮圈間過渡時的平均加速度。

鋼絲繩圈間過渡時會的速度差為

Δv=(l2-l1)·ω

(10)

鋼絲繩繞過折線過渡區的時間為

Δt=θ/ω

(11)

因此圈間過渡時的平均加速度值為

(12)

(13)

l2=2r

(14)

式中：ω為提升機卷筒纏繞的角速度；θ為折線繩槽對應的圓心角；r為鋼絲繩半徑；ε為繩槽間隙。

當鋼絲繩圈間過渡處于圖4中的A階段時加速度為正，處于B階段時加速度為負。

由提升機試驗臺數據可知，提升機卷筒纏繞的角速度為4.5 rad/s，折線繩槽對應的圓心角為π/10，將提升機的數據代入式(14)中得到，鋼絲繩在折線過渡區的加減速度值為±0.173 m/s2。

鋼絲繩每纏繞一圈所用的時間T為

T=2π·R/v

(15)

對稱式繩槽每圈纏繞會出現兩次加速度變化，其間隔相等，所以將其看作周期為T/2的信號；非對稱繩槽由于兩個折線過渡區不對稱，其加速度變化的時間間隔為

ΔT=(150°/360°)·T=5T/12

(16)

所以需要將加速度變化看作兩個周期為T的信號疊加，兩者出現的時間差為5T/12。圈間過渡加速度在提升機勻速提升階段內的變化形式如圖5所示。

(a)非對稱雙折線圈間過渡(b)對稱雙折線圈間過渡

在提升機的減速提升階段，由于提升速度的逐漸減小，鋼絲繩在圈間過渡時的加速度也會逐漸減小，其變化形式如圖6所示。

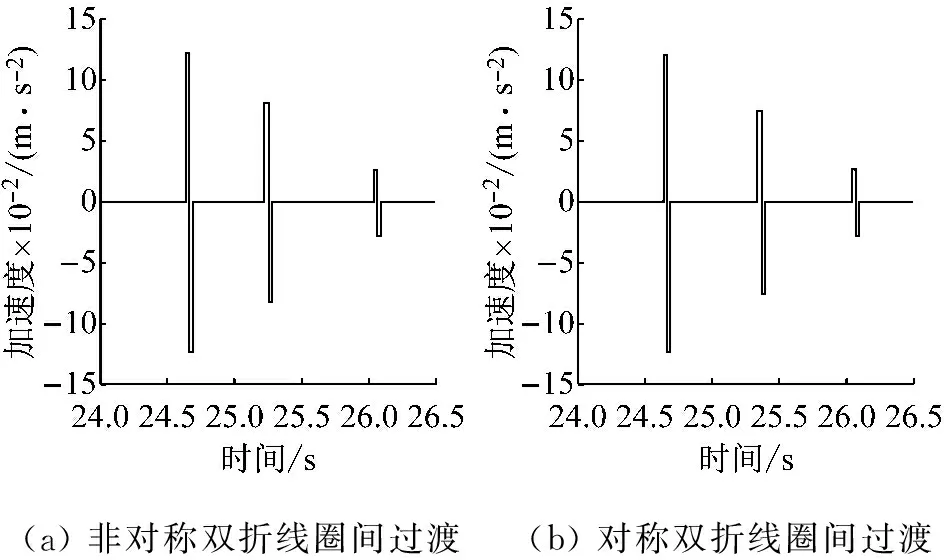
(a)非對稱雙折線圈間過渡(b)對稱雙折線圈間過渡

2 鋼絲繩動力學建模

本文選取直徑10 mm的6×7+IWS鋼絲繩為研究對象，經過計算和查詢[3-4]，得到動張力微分方程相關參數如表1所示。

依據式(1)～式(3)，并結合鋼絲繩的實際參數，建立無圈間過渡、對稱雙折線圈間過渡和非對稱雙折線圈間過渡三種狀態下的Simulink動張力仿真模型。以非對稱雙折線圈間過渡動張力仿真模型為例，圖7為鋼絲繩加速、勻速及減速階段的動張力輸出圖，模型中clock模塊控制模型運行的總時間，內部設置2.5 s和24 s作為各提升階段動張力輸出的判別條件，模型中的u為運行時間；圖8為鋼絲繩各階段繩長的輸出圖，模型內部同樣以2.5 s和24 s為各階段繩長公式計算的判別條件，模型中u為運行時間；圖9為勻速階段的動張力計算模型，模型采用兩個generator模塊疊加作為非對稱雙折線圈間過渡的加速度信號并依據勻速提升階段的繩長等參數對微分方程進行數值仿真。無圈間過渡和對稱雙折線圈間過渡狀態下的建模過程與之類似，故在此不再一一列舉。

表1 動張力微分方程相關參數Tab.1 The related parameters of dynamic tension differential equation

圖7 鋼絲繩動張力模型Fig.7 Simulationmodelofthewireropedynamicforce圖8 鋼絲繩繩長變化模型Fig.8 Simulationmodeloftheropelength

圖9 鋼絲繩勻速運行階段動張力模型Fig.9 Simulation model of the wire rope dynamic force in the uniform phase

本文中依據提升過程時間設定仿真時長為26.5 s，采用變步長解算器并采用四階龍格庫塔算法。

3 計算結果及分析

運行計算動張力的Simulink模型，得到無圈間過渡、對稱雙折線圈間過渡和非對稱雙折線圈間過渡三種情況下的動張力變化曲線如圖10所示。

如圖10(a)～圖10(c)所示，三種狀態下鋼絲繩的動張力變化趨勢大致相同。在提升過程中，鋼絲繩的動張力有明顯的波動，動張力總體呈下降趨勢，這是由于提升過程中鋼絲繩的長度減小造成的提升重量和等效剛度的不斷變化引起的；同時，鋼絲繩在加速到勻速和勻速到減速兩個過渡階段內的動張力都出現了較大的突變，其原因為鋼絲繩在各提升階段的加速度變化引起的慣性載荷和沖擊造成的；另外，在提升過程中，鋼絲繩動張力的波動頻率不斷增大，這是由于提升過程中鋼絲繩的長度不斷減小造成鋼絲繩的振動產生了變化[5-12]。

通過對比圖10(a)～圖10(c)三條曲線可知，多層纏繞鋼絲繩在圈間過渡時的加速度變化對加速提升階段幾乎沒有影響，但是對勻速和減速提升階段有較明顯的影響。如圖10(a)，如果不考慮圈間過渡，在勻速提升階段鋼絲繩動張力波動逐漸減小，減速提升階段動張力的振幅很小幾乎呈一種直線狀態，因為此時引起動張力變化的因素只有鋼絲繩的長度變化。考慮多層纏繞鋼絲繩的圈間過渡加速度以后，鋼絲繩的動張力會有明顯的不同，在提升階段后期鋼絲繩的動張力波動并不會明顯的減小，而是處于一種周期性變化的振動狀態。對比圖10(b)和圖10(c)兩種雙折線過渡方式的動張力曲線可知，在加速提升階段，非對稱雙折線鋼絲繩動張力和對稱雙折線鋼絲繩動張力沒有明顯的區別，在勻速提升階段，從大約第8 s開始，非對稱雙折線圈間過渡動張力相較于對稱雙折線圈間過渡動張力波動幅度更小，在減速提升階段，非對稱雙折線圈間過渡鋼絲繩動張力波動幅度相較于非對稱雙折線圈間過渡波動幅度以更快的速度減小且以較大幅度波動所持續的時間很短。

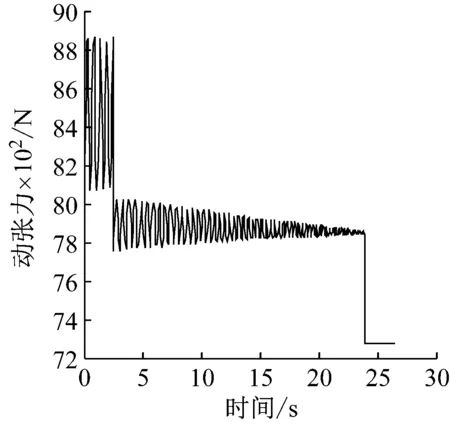
(a) 無圈間過渡

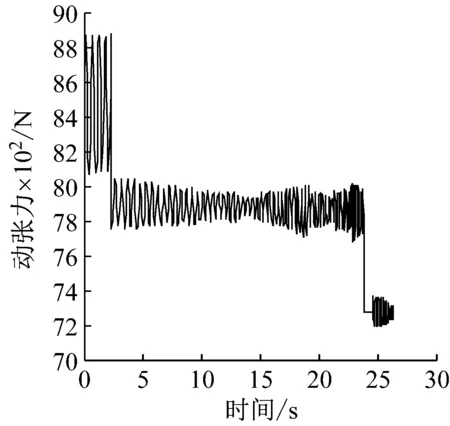
(b) 對稱雙折線圈間過渡

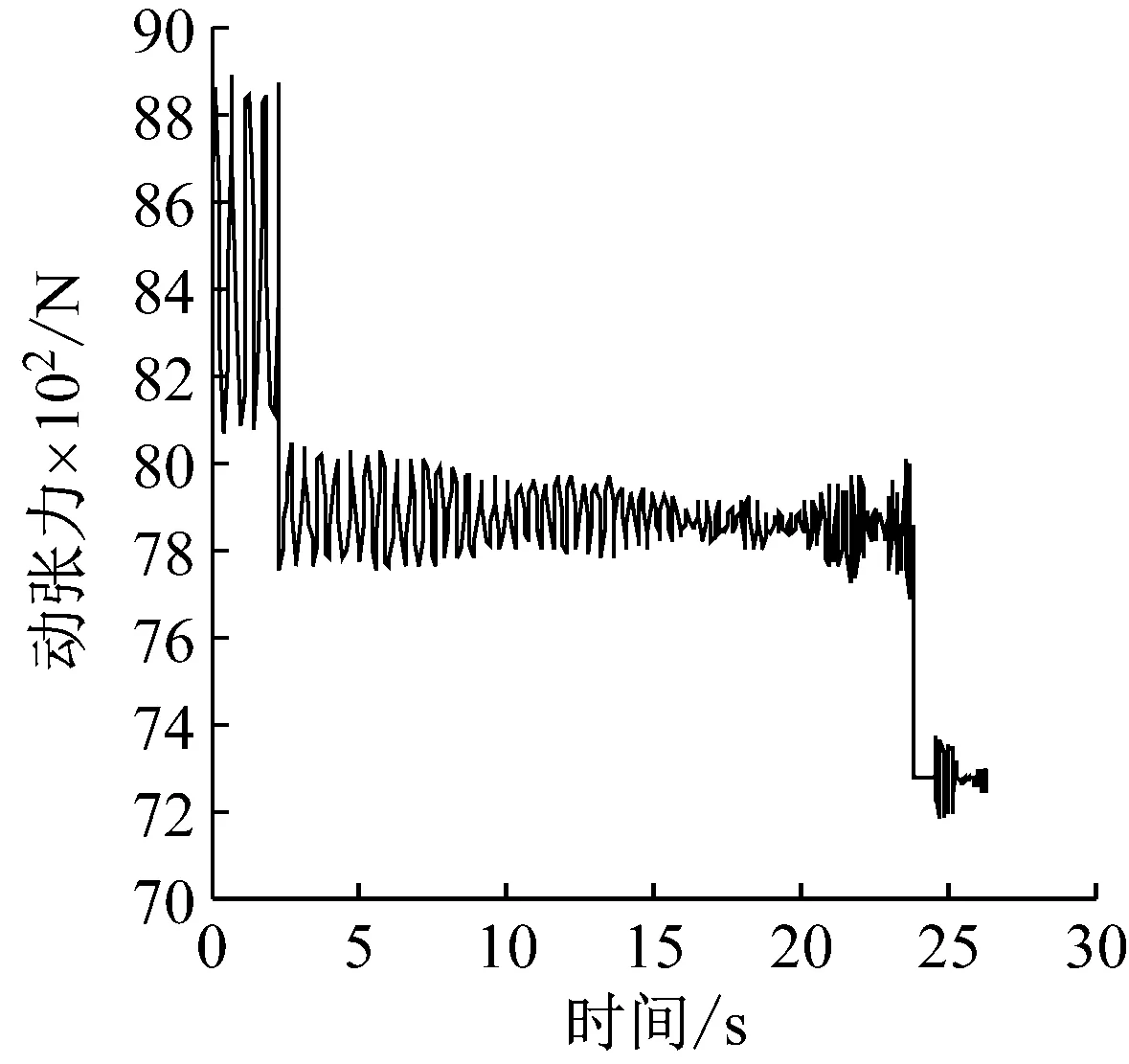
(c) 非對稱雙折線圈間過渡圖10 鋼絲繩動張力變化曲線Fig.10 Evolution of the rope load with time

4 結 論

(1) 本文對多層纏繞鋼絲繩進行圈間過渡時的加速度進行計算，并結合鋼絲繩在提升過程中的動張力微分方程，建立了提升過程中鋼絲繩動張力的Simulink仿真模型，得到了鋼絲繩動張力變化曲線。

(2) 通過對鋼絲繩動張力的變化曲線進行比較，發現多層纏繞鋼絲繩圈間過渡時的加速度變化對鋼絲繩的動張力有明顯的影響，在分析過程中不能忽略。

(3) 采用雙折線過渡繩槽進行多層纏繞鋼絲繩圈間過渡時，非對稱雙折線圈間過渡比對稱雙折線圈間過渡的動張力波動幅度更小，且出現動張力波動較大的范圍持續時間較短，此現象在提升過程的后期尤為明顯。

(4) 以本文方法得到的鋼絲繩圈間過渡動張力波動曲線，并未將鋼絲繩阻尼、鋼絲繩與卷筒之間的摩擦等影響因素考慮在內，故動張力波動曲線存在一定的偏差，因此今后還需通過試驗作進一步的研究。

[1] 聶虹.礦井提升機的發展與現狀[J]. 礦山機械, 2015，43(7)：13-17.

NIE Hong. Development and current situation of mine host[J]. Mining & Processing Equipment, 2015，43(7)：13-17.

[2] 嚴世榕, 聞邦椿. 豎井提升鋼絲繩容器系統在提升過程中的動力學仿真[J]. 中國有色金屬學報, 1998(增刊2):618-622.

YAN Shirong, WEN Bangchun. Dynamic simulation of shaft hoisting rope container system in the process of hoisting[J]. Transactions of Nonferrous Metals Society of China, 1998(Sup2):618-622.

[3] 國家質量監督檢驗檢疫總局.重要用途鋼絲繩：GB 8918—2006[S].北京：國家標準化管理委員會，2006.

[4] VANDERVELDT H H, CHUNG B S, READER W T. Some dynamic properties of axially loaded wire ropes[J]. Experimental Mechanics, 1972, 13(1):24-30.

[5] 包繼虎, 張鵬, 朱昌明. 變長度提升系統鋼絲繩縱向振動特性[J]. 振動與沖擊, 2013, 32(15):173-177.

BAO Jihu, ZHANG Peng, ZHU Changming. Longitudinal vibration of rope hoisting systems with time-varing length[J].Journal of Vibration and Shock, 2013,32(15):173-177.

[6] ZHU W D, NI J. Energetics and stability of translating media with an arbitrarily varying length[J]. Journal of Vibration & Acoustics, 2000, 122(3):295-304.

[7] 吳娟, 寇子明, 梁敏. 摩擦提升系統鋼絲繩橫向動力學分析[J]. 振動與沖擊, 2016, 35(2):184-188.

WU Juan, KOU Ziming, LIANG Min. Transverse dynamics analysis of rope in multi-rope friction hoisting system[J]. Journal of Vibration and Shock, 2016, 35(2):184-188.

[8] CARTMELL M P, MORRISH L, TAYLOR A J. Dynamics of spreader motion in a gantry crane[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science 1989-1996 (vols 203-210), 1998, 212(2): 85-105.

[9] 賈尚雨, 謝小鵬, 梁廣熾. 起重機鋼絲繩的動力學建模與仿真[J]. 煤礦機械, 2010, 31(4):58-61.

JIA Shangyu, XIE Xiaopeng, LIANG Guangchi. Dynamics modeling and simulation of crane wire rope[J].Coal Mine Machinery, 2010, 31(4):58-61.

[10] 嚴世榕,聞邦椿.下放容器時提升鋼絲繩的動力學仿真[J].煤炭學報,1998,23(5):530-534.

YAN Shirong, WEN Bangchun. Dynamic simulation of hoisting wire rope in the descending cycle of container[J]. Journal of China Coal Society,1998,23(5): 530-534.

[11] 劉會燈. MATLAB編程基礎與典型應用[M]. 北京：人民郵電出版社, 2008.

[12] 楊義勇, 金德聞. 機械系統動力學[M]. 北京：清華大學出版社, 2009.

Influenceofropecircletransitiononthedynamictensionofmultilayerwindingwireropesinsuperdeepminehoistingmachines

LI Xiaoguang1,2，GONG Xiansheng1,2，WU Shuiyuan1,2，LUO Yuchi1,2

(1.The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China; 2.College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)

The acceleration variation during the rope circle transition of multi-layer windings in super deep mine hoists was studied. With the aid of the differential equation for the dynamic tension of lifting wire ropes and the MATLAB Simulink module, the dynamic tension of a multi-layer winding wire rope with symmetric and non symmetric bilinear transitional rope slots was modeled, simulated and analyzed. The results show that the acceleration during the rope circle transition of the multi-layer winding wire rope has a significant impact on the dynamic tension of the wire rope. The dynamic tension of the rope with the circle transition in the symmetrical bilinear rope groove is larger than that in the non symmetrical bilinear rope groove. The results are of reference value for the study of multi-layer windings of super deep well lifting systems.

multi-layer winding; transiting; double broken line transition rope slot; dynamic tension

TH113

A

10.13465/j.cnki.jvs.2017.19.038

國家重點基礎研究發展計劃(973計劃)資助項目(2014CB049403)

2016-05-10 修改稿收到日期：2016-08-13

李曉光 男，碩士生，1990年生

龔憲生 男，博士，教授，博士生導師，1956年生