基于自適應篩選EMD和CFDC的變壓器繞組狀態檢測

楊 毅，王豐華，段若晨，杜勝磊，劉 石，楊 賢

(1.廣東電網公司電力科學研究院，廣州 510080；2.上海交通大學 電力傳輸與功率變換控制教育部重點實驗室，上海 200240)

基于自適應篩選EMD和CFDC的變壓器繞組狀態檢測

楊 毅1，王豐華2，段若晨2，杜勝磊1，劉 石1，楊 賢1

(1.廣東電網公司電力科學研究院，廣州 510080；2.上海交通大學 電力傳輸與功率變換控制教育部重點實驗室，上海 200240)

為更加準確地檢測變壓器的繞組狀態，提出了自適應篩選EMD算法來對變壓器突發短路下的非平穩和強時變振動信號進行分解，進而根據得到的Hilbert邊際譜定義了中心頻率分布系數(Central Frequency Distribution Coefficient，CFDC)來對變壓器繞組狀態進行檢測。仿真分析和某大型變壓器實測振動信號的計算結果表明，增加了自適應篩選因子的改進EMD算法能夠有效地抑制模態混疊現象，提高了振動信號分解的準確性，所定義的CFDC及其變化可以清晰地反映出變壓器繞組狀態改變的演變過程，便于及時有效檢測繞組狀態，確保變壓器的安全可靠運行。

變壓器；繞組狀態；自適應篩選EMD；中心頻率分布系數；振動信號

統計結果表明[1]，源于出口短路故障的變壓器繞組變形或松動是變壓器繞組故障的主要原因，且隨電網容量的增大及變壓器使用年限的增加呈現逐年增長趨勢，因此，迫切需要一種能夠及時有效檢測變壓器繞組運行狀態的方法，確保變壓器及電力系統的安全可靠運行。

作業布置的“尺度”指數量限度、時間長度、知識跨度、難易程度。要實現最佳的教學效果，必須協調好四者之間的關系，將“度”控制在一個合理的水平上，促進學生學習質量和學習素養的提高。

運行中的變壓器振動主要由繞組振動和鐵芯振動組成，且變壓器箱壁的振動信號與繞組和鐵芯的機械狀態密切相關，故可通過檢測變壓器箱壁表面的振動信號來判別繞組和鐵芯的運行狀態，即為振動分析法。因該方法具有敏感性高、抗干擾能力強等優點，日益引起了國內外研究者的關注[2-3]。在應用振動分析法對變壓器繞組狀態進行檢測分析時，如何對監測到的振動信號進行解釋分析進而給出合理效的繞組狀態檢測方法是研究熱點之一。現有研究主要分為兩大類，第一類是根據變壓器振動與其工作電流、外加電壓和油溫的關系，建立變壓器的箱壁振動計算模型，根據計算結果與實測信號進行對比來識別變壓器繞組狀態的變化[4-7]。其中，García等[4-5]根據變壓器空載試驗和短路試驗下的箱壁振動特性測試結果給出了振動計算模型的數學表達式；文獻[6]構建了基于貝葉斯網絡的變壓器振動概率模型；文獻[7]提出了基頻折算模型來判斷變壓器繞組故障類型并進行初步故障定位。但在應用此類模型對變壓器繞組狀態進行診斷時，考慮到變壓器結結構與現場運行工況的多樣性，合理的閾值設置是難點。第二類是對變壓器振動信號的時頻特性進行分析，進而提出有效的振動信號特征量提取方法和繞組狀態檢測方法。文獻[8]使用小波變換得到了振動信號各個頻段上的能量分布狀態；文獻[9]利用振動烈度和Gabor變換對突發短路下的振動信號進行了計算分析；文獻[10]引入Morlet小波展示了突發短路下振動信號的頻譜特性。諸如此類的時頻分析方法用于分析頻率緩變的信號會有較好的效果，但會存在諸如能量泄露、自適應差的缺陷，精度有限。

突發短路下的變壓器振動信號呈現非平穩性和強時變特性，蘊藏著豐富的變壓器繞組狀態信息，有必要尋求準確高效的振動信號特征量提取方法實現繞組狀態的合理描述。經驗模態分解法(Empirical Mode Decomposition, EMD)得到的信號特性不僅與分析頻率有關，而且可以隨信號本身變化而改變，可有效地表述出信號的局部特征，具有較高的分辨率較高[11-12]。因此，本文嘗試使用自適應篩選EMD算法分析突發短路下變壓器的振動信號，期望在有效抑制EMD算法固有模態混疊效應的同時提高EMD分解過程的準確性。進而根據振動信號的Hilbert能量譜定義合理的評價指標來尋求變壓器繞組的狀態檢測方法。最后對某110 kV變壓器短路沖擊試驗下的振動信號進行分析，對分解方法及評價指標的合理性進行驗證。

1 自適應篩選EMD算法

1.1EMD算法原理

EMD算法的基本思想是將原始信號分解成一系列滿足“單分量信號”——固有模態函數(Intrinsic Mode Function,IMF)的組合，使得瞬時頻率在IMF上有合理的物理意義，然后可經Hilbert變換求取模式分量的瞬時頻率或邊際譜等特征。其分解過程為：

步驟1確定信號x(t)的所有局部極大值點u(t)和局部極小值點l(t)，使用3次樣條插值算法分別得到上包絡線emax(t)和下包絡線emin(t)。

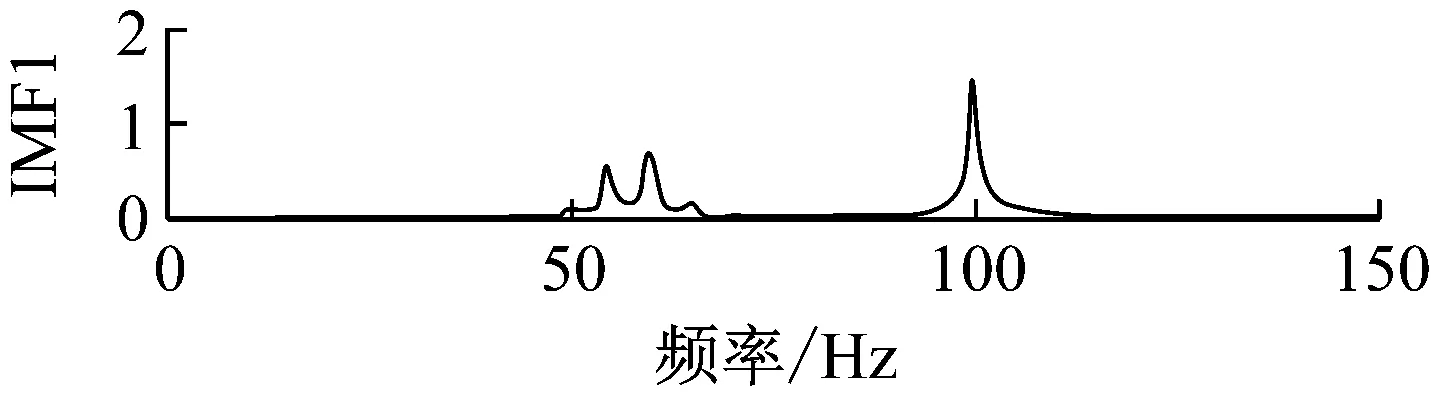
圖2為使用傳統EMD算法對仿真信號進行分解所得IMF1和IMF2的時域波形及邊際譜圖。限于篇幅，僅對包含主要頻率分量的前兩個IMF進行分析，其余分量如調幅調頻分量等位于后續IMF中，由于幅值較小，特征不夠明顯，因此暫不進行分析。由圖可見，分解出的IMF2分量幅值遠小于仿真信號x2(t)幅值，因而該方法會導致分解時域波形嚴重失真。同時由邊際譜可以看到，傳統EMD分解出來的IMF分量存在著嚴重的頻率混疊現象。這是由于當構成目標信號的頻率分量較為接近(f1/f2<2)時，傳統EMD算法很容易將該信號解釋成由一定調制程度的本征模態函數組成，因此無法對各分量進行有效區分，從而不能夠準確提取頻域特征。

Basketball was invented by a Canadian doctor named James Naismith，who was born in 1861.（籃球是一個名叫詹姆斯·奈史密斯的加拿大醫生發明的，他出生于1861年。）

y1(t)=x(t)-m(t)

(1)

對式(11)取積分，可得Hilbert邊際譜h(w)為

將利用自適應篩選EMD法得到的各IMF(記為ci(t))作Hilbert變換，并構造解析信號zi(t)，進而得到幅值函數ai(t)、相位函數Φi(t)以及瞬時頻率wi(t)，即

(2)

式中,rn(t)為殘差。

1.2自適應篩選EMD算法

EMD分解過程的核心是篩選出滿足條件的最優IMF。在傳統EMD算法中，每一步均需要減去上下包絡的均值m(t)以消除IMF的波動趨勢。但當分解信號為波動較為顯著的瞬時信號時，其包絡值在某一點有可能存在較大變化，而盲目求取上下包絡的均值有可能增大分解過程中的迭代誤差，使得EMD分解過程有可能會產生模態混疊現象，進而導致其在故障分析中可能出現誤判的情形，影響其實際應用。為有效抑制模態混疊缺陷，本文在此針對變壓器繞組突發短路下振動信號的特性提出自適應篩選EMD算法對其進行分析。

定義自適應篩選因子λ，則式(1)變為

y1(t)=x(t)-λ(u(t)+l(t))

(3)

式中,λ∈(0,0.5]。

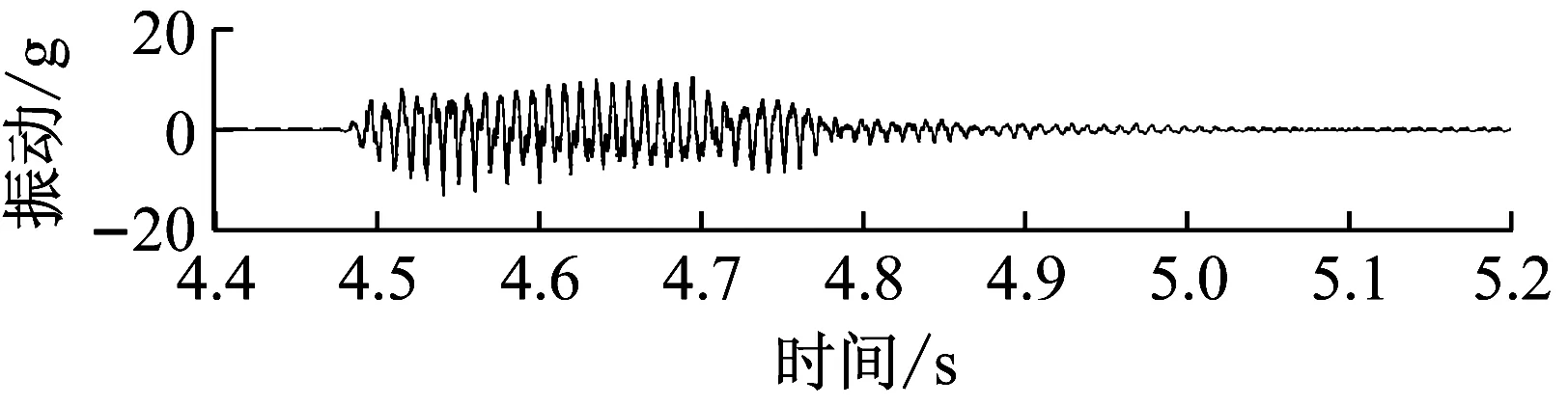
共對C相繞組進行高對中突發短路試驗9次，記IN為試驗所用的變壓器經核算后能承受的最大額定電流，分別為70%IN1次、90%IN2次、110%IN2次、120%IN3次、130%IN1次。外加130%IN試驗后，C相繞組出現短路電抗超標的情形。圖5為C相繞組施加不同短路電流時第1次高對中突發短路試驗時的振動波形。由圖可見，短路沖擊下的變壓器振動信號呈現明顯的非線性和非平穩特性，其振動幅值隨外加短路電流的增大而增大。

根據IMF的定義可得，理想狀態下每一個IMF均正交于其它IMF，即

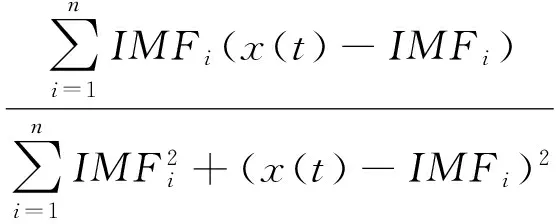
(4)

因此可利用正交性準則求取最優篩選因子λp。定義正交系數P為

（2）《財政部 稅務總局關于延續支持農村金融發展有關稅收政策的通知》[7]中明確規定2017年1月1日-2019年12月31日，對金融機構農戶小額貸款的利息收入，在計算應納稅所得額時，按90%計入收入總額。

(5)

同時，對λ在(0,0.5]區間內連續取值，取值間隔定義為Δ=0.01，當所選λ使得P最小時，則該λ即為最優篩選因子λp，同時計算相應的IMF即為所求最優IMF。進而重復步驟1～步驟4求得所有IMF分量。

是人，都有短板和長項，繁復的生活中，沒有無用的人，只有沒用好的人。缺陷，常常讓人抉擇單純，心無雜念。而心無雜念的人，最能在人生過程中舉重若輕。可以說，缺陷是人生的拐點，可以成就的，往往是別樣的美麗，別樣的人生。維納斯雕像因斷臂而愈顯美麗，《千手觀音》因聾啞藝人表演而愈顯出類拔萃，流星因生命短暫更加動人心魄……

由于該算法所得的IMF分量確保了正交性的最大化，因此每個IMF中所包含的頻率分量也最為單一，從而有效抑制了模態混疊現象。同時由于最優篩選因子是由數據本身決定的，因此該算法具有很強的自適應性，可以較好地應用對沖擊振動信號進行分解。

1.3Hilbert邊際譜

步驟4將c1(t)從x(t)中分離出來，得到差值r1(t)=x(t)-c1(t)，將r1(t)作為原始數據，重復步驟1～步驟3，得到第2個IMF分量c2(t)，如此重復得到所有的IMF，故有

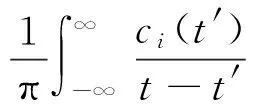
(6)

zi(t)=ci(t)+jH[ci(t)]=ai(t)ejΦi(t)

(7)

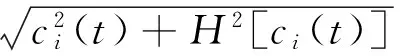
(8)

(9)

(10)

忽略分解余量，將zi(t)的實部展開，得到Hilbert譜為

這一下震驚了李老師，李老師就是有學生來告狀，然后就發現了這些罪證。看見這些東西，李老師的臉也紅了，整個辦公室的老師們得知情況后都傻了，李老師意識到情況很嚴重。但怎么樣也想不到原因是周小羽講的這樣，因為她當時也沒容許周小羽再分辯。她當時就在心里想，哪個老師看見會不生氣啊！在她看來，這些畫充滿著黃色和暴力，有些是男女一起的，有些是打架的，有一張李老師記得很清楚，那就是一個人被綁在板凳上，旁邊一個人在拼命地用灌木刺打著。那畫面讓她想起電視上那些私設刑罰的場景。這么一個小孩子，哪里學來的這些東西，所以，她是一定要上門家訪的。這個孩子這樣下去就不行了！

(11)

步驟3判斷y1(t)是否為IMF分量，如不是，則將y1(t)作為原始分量，重復步驟1和步驟2，直到y1(t)滿足IMF分量條件，記y1(t)為c1(t)，則c1(t)記為第1個IMF分量。

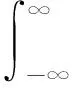
(12)

（4）壁水蘊德星君，司圖書，驚墊日紏稠梗治。（《太上說玄天大聖真武本傳神呪妙經註》卷一，《中華道藏》30/533）

2 仿真分析驗證

為了驗證本文所述前述自適應篩選EMD算法的有效性，本文在此構造多頻簡諧振動仿真信號x(t)進行分析，如式(13)所示。該信號中所包含的頻譜分量主要包含頻率分量為f1=100 Hz(與變壓器正常振動頻率相同)，f2=60 Hz以及一些5 Hz的低頻噪聲分量。采樣頻率為2 kHz，如圖1所示。

馬戴的思鄉情結與隱逸情懷也是聯系在一起的，他在詩中每次提到回到家鄉就是要去過隱居生活，如其《客行》云：

(13)

圖1 仿真信號波形Fig.1 Waveform of simulation signal

步驟2將兩條包絡線的平均值記為m(t),將原序列減去m(t)得到一個新序列

其二，課程結構設計不合理。法學是實踐性很強的專業，應用型法學人才的培養更需要不斷強化課內實踐和課外實踐。但有些獨立學院法學專業鑒于課內實踐場地和設施簡陋、課外實訓基地少、校外缺乏長期穩定的實踐基地等情況，套用其他普通高校的課程體系，致使課程體系中實踐類課程偏少，理論類課程偏多，課程結構存在著明顯不合理的現象。

(a)

(b)

(c)

(d)圖2 傳統EMD所得IMF時域波形及邊際譜圖Fig.2 Waveform and marginal spectrum of IMFs based on conventional EMD

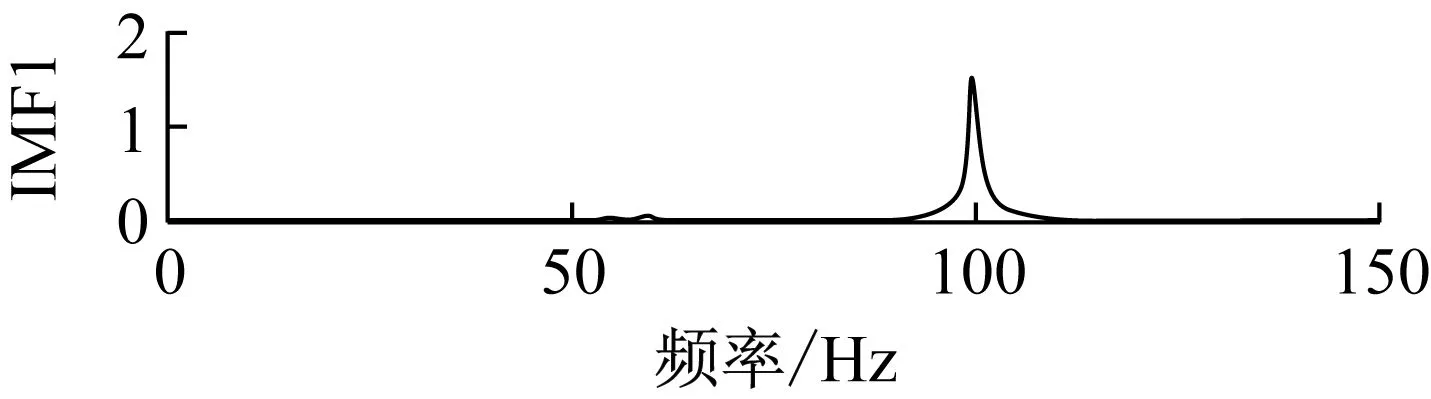
圖3為采用自適應篩選EMD算法對仿真信號進行分解所得IMF1和IMF2的時域波形及邊際譜圖。由圖可見，該方法較好地解決了分解過程中的模態混疊現象，其分解出來的IMF幅值及頻率與實際值能夠良好吻合，充分驗證了本方法的有效性和準確性。

為進一步說明自適應篩選EMD在IMF分解過程中的有效性，表1中同時給出了自適應篩選EMD和傳統EMD算法兩種方法分解所得IMF分量的正交系數P的對比結果。顯然，本文所提出的自適應篩選EMD算法分解得到的IMF分量具有更強的正交性，可以更好地抑制模態混疊現象，提高變壓器振動信號分解過程的準確性。

易知，Hilbert邊際譜反映了幅值隨頻率的變化情況。

表1 正交系數對比結果Tab.1 Comparisons of orthogonal coefficients

(a)

(b)

(c)

(d)圖3 自適應篩選EMD所得IMF時域波形及邊際譜圖Fig.3 Waveform and marginal spectrum of IMFs based on self-adaptive sifting EMD

需要指出的是，通過連續取值所得到的自適應篩選因子，并不會影響EMD過程所求得的IMF函數性質，其所得各IMF依然滿足約束條件，且各IMF成分變化不大。同時注意到，自適應篩選EMD所得各IMF的殘差相較于傳統EMD也大幅減小，說明該方法可對信號進行更為準確徹底的分解。

3 試驗描述

試驗對象為一臺額定電壓為121 kV的三繞組變壓器，如圖4所示，其銘牌參數如表2所示。試驗時將變壓器低壓側短路，分別對三相繞組進行多次不同短路電流的高對中和高對低突發短路試驗。限于篇幅，考慮到C相繞組在外加130%額定電流時高對中短路沖擊試驗后出現短路電抗超標的情形，本文在此重點以C相高對中各次突發短路試驗下的振動信號進行分析。選用的傳感器為PCB振動加速度傳感器，靈敏度為10 mV/g，放置于變壓器箱壁，并利用經自行研制的基于NI Compact Rio的數據采集系統采集振動信號。

對于傳統EMD算法而言，通常有λ=0.5。當λ<0.5時，同樣能夠消除IMF的波動趨勢并減小EMD分解過程中的迭代誤差。因此，λ存在一個最優值使得每一步的IMF最符合約束條件，因此需要定義相關指標，尋找最優篩選因子λp。

圖4 試驗變壓器Fig.4 The real picture of transformer under test

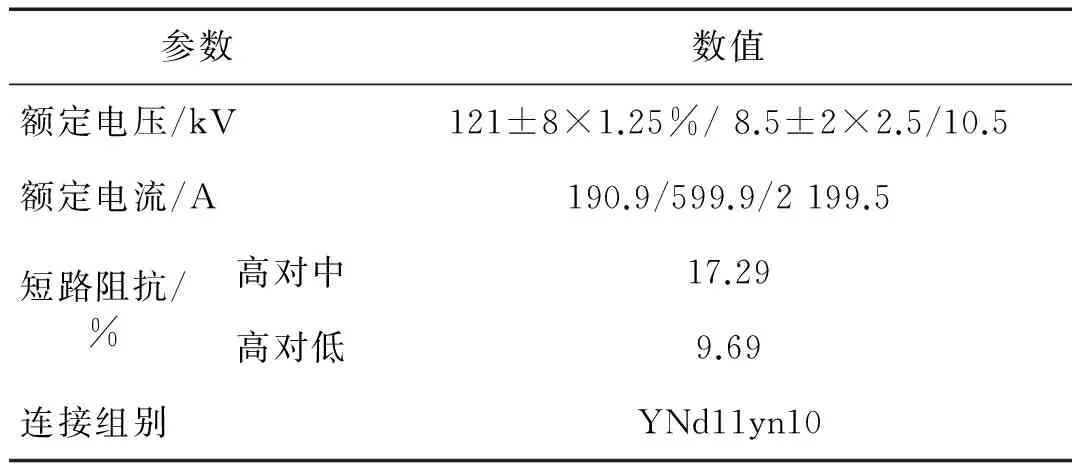
表2 試驗變壓器的銘牌參數Tab.2 Nameplate parameters of experimental transformer

(a) 70%電流

(b) 90%電流

(c) 110%電流

(d) 120%電流

(e) 130%電流圖5 多次短路沖擊下的振動信號時域波形Fig.5 Vibration signal waveforms of several short-circuit impacts

4 結果分析

4.1振動信號的邊際譜

分別對圖5所示的從90%IN開始的4次短路沖擊試驗下的振動信號自適應篩選EMD分解，可所得到如圖6所示的的邊際譜圖如圖6所示。由圖可見，不同短路電流下，振動信號的主要頻率分量大都為100 Hz分量，其對應的幅值均隨短路電流的增大而改變。但是，外加120%IN短路沖擊試驗時，振動信號主要頻譜分量100 Hz和200 Hz的幅值極為接近。外加130%IN短路沖擊試驗時，振動信號中的200 Hz分量幅值增幅明顯，且超越100 Hz成為主要頻譜分量。

(a) 90%電流

(b) 110%電流

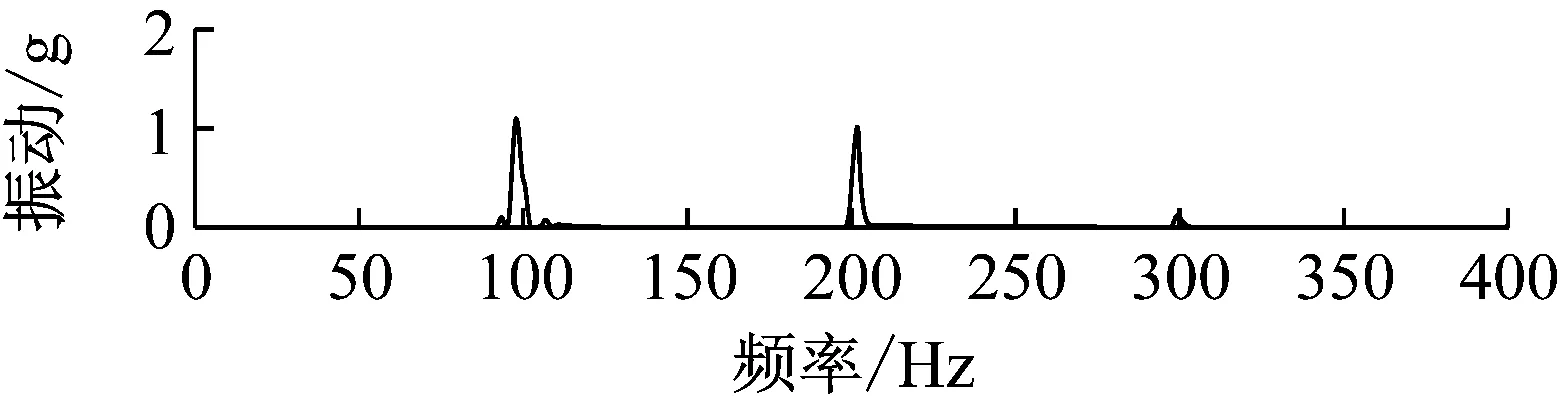
(c) 120%電流

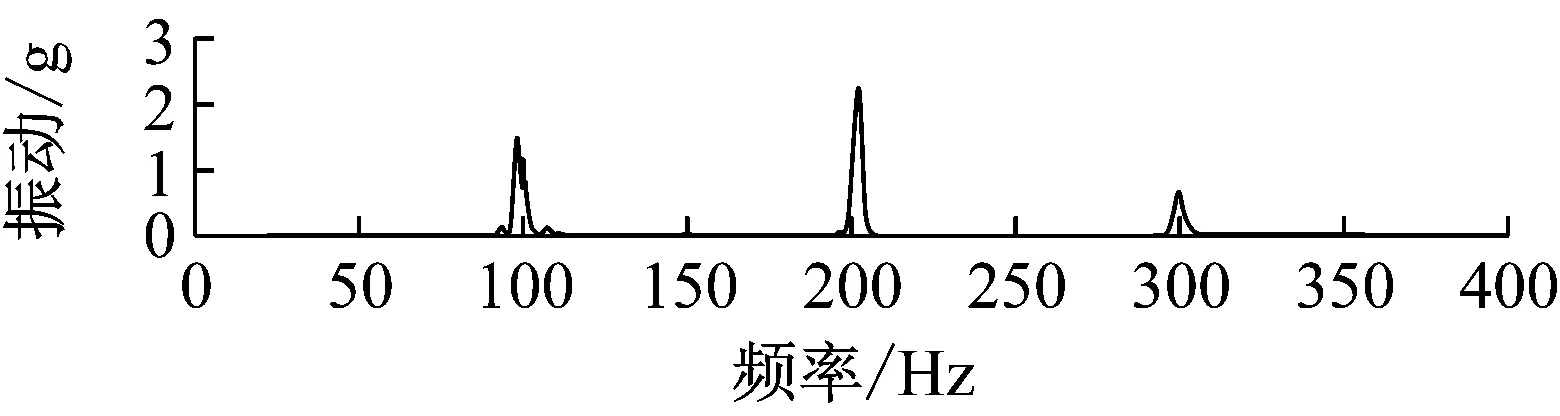
(d) 130%電流圖6 振動信號邊際譜Fig.6 Marginal spectrum of vibration signal

4.2中心頻率分布系數

對C相繞組各次短路沖擊試驗時振動信號的邊際譜分布可見，100 Hz分量為主要頻譜分量，可將其定義為中心頻率，此外，邊際譜中還包含有其它頻率分量。為定量描述振動信號頻譜分布隨繞組狀態的變化，本文在此提出了中心頻率分布系數(Central Frequency Distribution Coefficient，CFDC)這一指標，即為

(14)

式中:Sc為邊際譜中心頻率CF±10 Hz范圍內的包絡面積;S為邊際譜總包絡面積;IN為變壓器額定電流;Isc max為突發短路電流最大值;k為系數，取值范圍為0.9～0.95。其中，選取10 Hz作為計算范圍的原因主要是因為計算得到的振動邊際譜中的每個頻率寬度均為±10 Hz左右。如果范圍過小，則不能完全涵蓋該頻率分量，若范圍過大，則有可能混入其它頻率分量。

2.2 2組治療前后膝關節屈曲AROM比較 術后4及12周后，2組患者AROM均較前一個時間點呈明顯增加趨勢(均P<0.05)；術后4周2組組間比較差異無統計學意義，術后12周觀察組患者AROM明顯高于同時間點對照組(P<0.05)。見表3。

顯然，CFDC的值越小，說明邊際譜中心頻率的包絡面積越小，預示著振動信號頻譜分布中除中心頻率之外的其它頻譜分量的日益豐富。在此以IN=Isc max的情形為例進行說明，考慮到除中心頻率之外的頻譜分量的存在，對正常狀態的變壓器繞組來說，CFDC的取值應滿足CFDC≥0.8的情形。

表3為試驗所用的變壓器C相繞組高對中各次短路沖擊試驗中振動信號CFDC的變化情況，表中同時列出了各次短路沖擊下振動信號100 Hz分量幅值的變化規律，其中，CFDC和100 Hz分量幅值的變化率均是相對于前一次短路沖擊試驗時的振動信號而言的。由表可見，隨著短路電流的增大，所定義的CFDC呈現下降趨勢，100 Hz分量幅值呈現升高趨勢。在外加110%IN和120%IN的各次短路沖擊試驗中，CFDC的取值在0.7～0.77變化，說明C相繞組可能存在松動或變形的情形，值得關注。外加120%IN第3次短路沖擊試驗時，CFDC的變化率超過了20%，其變化體現了變壓器繞組變形累積效應的同時，說明了C相繞組潛在的松動或變形呈現加劇的趨勢。外加130%IN時，CFDC為0.42，其變化率超過了50%，說明有繞組變形出現。此時，C相繞組短路電抗的變化也出現了超標的情形。

表3 C相繞組各次短路沖擊試驗下CFDC和100 Hz分量幅值變化表Tab.3 Variations of 100 Hz component and CFDC in vibration signal of phase-C winding

為進一步說明所定義的CFDC的有效性，本文在此同時給出了該臺變壓器B相繞組高對中各次短路沖擊試驗時振動信號的計算結果，如表4所示。其中，B相繞組在第5次120%IN短路沖擊試驗后出現短路電抗超標的情形。類似地，隨著B相短路電流的增大，所定義的CFDC呈現下降趨勢，100 Hz分量幅值呈現升高趨勢。當CFDC的取值在0.7～0.8時，B相繞組可能存在松動或變形。當其隨短路電流的增幅超過20%的時候，B相繞組潛在的松動或變形情況加劇。外加120%IN第5次短路沖擊時，CFDC為0.39，其變化率超過了50%，說明有繞組變形出現。此時，B相繞組短路電抗的變化也出現了超標的情形。此外，相對于振動信號中100 Hz分量幅值隨短路電流的變化，所定義的CFDC更能準確反映變壓器繞組狀態變化的演變過程。

表4 B相繞組各次短路沖擊試驗下CFDC和100 Hz分量幅值變化表Tab.4 Variations of 100 Hz component and CFDC in vibration signal of phase-B winding

4.3與傳統EMD的比較

為進一步說明本文所提自適應篩選EMD算法的有效性，分別對圖5所示的C相繞組振動信號使用自適應篩選EMD和傳統EMD算法進行分解并計算CFDC，結果如圖7所示。由圖可見，由于頻譜混疊的存在，經傳統EMD計算得到的CFDC普遍小于經自適應篩選EMD的計算結果。此外，經自適應篩選EMD的計算得到的CFDC隨短路電流的增大呈現平穩下降趨勢，在130%IN短路沖擊試驗時，CFDC顯著下降，表明有除中心頻率之外的其它頻段分量出現且幅值顯著增加，說明有變壓器繞組變形故障出現。

圖7 中心頻率分布系數變化圖Fig.7 Variation of CFDC

需要指出的是，變壓器繞組狀態發生改變后新的幅值較大的頻譜分量的出現，應該是主要源于變壓器繞組發生共振的結果，這與與變壓器的繞組結構或材料屬性及作用在繞組上的短路電動力密切相關，需要在后續研究中繼續關注。

財會人員和檔案工作人員，應按歸檔范圍，做好會計檔案的收集工作。隨著電子計算機技術的推廣和普及，采用計算機進行會計核算，產生了大量的電子文件，電子文件也要按有關規定歸檔。但在歸檔時，還應保存打印出來的相應的紙質會計檔案。

本研究嚴格按照Delphi專家咨詢法,構建了一套科學、合理的康復專科護士核心能力評價指標體系，包括8個一級指標、21個二級指標和66個三級指標。專家對各個指標的意見具有高度的一致性，可信度高，同時具有一定的科學性和權威性，并且各指標的權重設置合理，為康復專科護士培養、資質認證和能力評價提供參考依據。本研究并未對指標內在品質進行研究，因此，對康復專科護士核心能力評價指標的信效度檢驗，將是下一步研究的重點內容。

5 結 論

根據本文所提出的自適應篩選EMD算法和所定義的CFDC指標對實體變壓器突發短路試驗下振動信號的分析結果表明：

(1) 所提出的自適應篩選EMD算法能夠有效解決傳統EMD算法中的模態混疊問題，提高了分解結果的準確性，可以更好的運用于分析短路沖擊下的變壓器振動信號。

(2) 隨著短路沖擊電流的增大，各次短路沖擊試驗中振動信號的CFDC呈現下降趨勢。當CFDC的取值在0.7～0.8時，變壓器繞組可能存在松動或變形。當CFDC隨短路電流的增幅超過20%的時候，變壓器繞組潛在的松動或變形情況加劇。當CFDC的變化趨勢超過50%時，變壓器繞組有變形故障出現。

(3) 相對于振動信號100 Hz分量幅值隨短路電流的變化規律來說，所定義的CFDC能更為準確的表征繞組狀態變化的演變過程。

鑒于變壓器繞組結構的多樣性及運行狀態的復雜性，根據所定義的CFDC及其變化檢測變壓器繞組狀態變化的普適性仍需進一步的驗證，這也是我們下一步的工作。

[1] 王夢云．110 kV及以上變壓器事故與缺陷統計分析[J]. 供用電，2007, 24(1): 1-5.

WANG Mengyun. Statistic analysis of transformer faults and defects at voltage 110 kV and above [J]. Distribution & Utilization, 2007, 24(1): 1-5.

[2] 汲勝昌，王世山，李清泉，等. 用振動信號分析法監測變壓器繞組狀況 [J]. 高電壓技術，2002，28(4): 12-15.

JI Shengchang, WANG Shishan, LI Qingquan, et al. The application of vibration method in monitoring the condition of transformer winding [J]. High Voltage Engineering, 2002, 28(4): 12-15.

[3] MARIANA I, ROBERT B, MIHAI O P, et al. Vibration monitoring for diagnosis of electrical equipment’s faults[C]∥Proceedings of the 12th International Conference on OPTIM. Brasov: OPTIM, 2010: 493-499.

[6] IBARGIEMGPUTIA P H, LINAN R, BETANCOURT E. Transformer diagnosis using probabilistic vibration model[C]∥ IEEE PES on Transmission and Distribution Conference and Exposition. New Orleans: IEEE, 2010: 1-8.

[7] 馬宏忠，耿志慧，陳楷，等. 基于振動的電力變壓器繞組變形故障診斷新方法 [J]. 電力系統自動化，2013，37(8): 89-95.

MA Hongzhong, GENG Zhihui, CHEN Kai, et al. A new fault diagnosis method for power transformer winding deformation based on vibration [J]. Automation of Electric Power Systems, 2013，37(8): 89-95.

[8] 顏秋容，劉欣，尹建國. 基于小波理論的電力變壓器振動信號特征研究 [J]. 高電壓技術，2007,33(1):165-168.

YAN Qiurong, LIU Xin, YIN Jianguo. Features of vibration signal of power transformer using the wavelet theory [J]. High Voltage Engineering, 2007, 33(1): 165-168.

[9] 邵宇鷹，徐劍，饒柱石，等. 短路沖擊下變壓器繞組狀態在線診斷[J]. 振動與沖擊，2011，30(2): 173-176.

SHAO Yuying, XU Jian, RAO Zhushi, et al. On-line diagnosis for a transformer winding’s state under short-circuit shock [J]. Journal of Vibration and Shock, 2011, 30(2): 173-176.

[10] 張坤，王豐華，廖天明，等. 應用復小波變換檢測突發短路時的電力變壓器繞組狀態 [J]. 電工技術學報，2014, 29(8)：327-332.

ZHANG Kun, WANG Fenghua, LIAO Tianming, et al. Detection of transformer winding deformation under short-circuit impulse base on complex wavelet algorithm [J]. Transactions of China Electrotechnical Society, 2014, 29(8)：327-332.

[11] 李莉，朱永利，宋亞奇. 變壓器繞組多故障條件下的振動信號特征提取[J]. 電力自動化設備，2014，34(8): 140-146.

LI Li, ZHU Yongli, SONG Yaqi. Feature extraction for vibration signal of transformer winding with multiple faults [J]. Electric Power Automation Equipment, 2014, 34(8): 140-146.

[12] 田玉芳. 變壓器繞組狀態的振動檢測法研究[D]. 濟南:山東大學，2014.

[13] RILLING G, FLANDRIN P, GONCALVES P. On empirical mode decomposition and its algorithms [C]∥ IEEE Workshop on Nonlinear Signal and Image Processing. Grado: NSIP, 2003.

Detectionoftransformerwindingconditionbasedontheself-adaptivesiftingEMDandCFDC

YANG Yi1，WANG Fenghua2，DUAN Ruochen2, DU Shenglei1，LIU Shi1，YANG Xian1

(1. Guangdong Electric Power Company Electric Power Research Institute，Guangzhou 510080，China;2. Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education，Shanghai Jiao Tong University, Shanghai 200240，China)

To detect the mechanical condition of transformer windings more accurately, an algorithm by the name of self-adaptive sifting EMD (SASEMD) was proposed to analyze the unstable and time-varying vibration signals of power transformers under an accident of sudden short-circuit. The central frequency distribution coefficient (CFDC) based on the obtained Hilbert marginal spectrum was defined to detect the winding conditions. According to the simulation analysis and the calculated results of the measured vibration signals of some large-scaled transformer, it is seen that the improved EMD with self-adaptive sifting factor can effectively restrain the aliasing effect and improve the accurateness of the signal decomposition. The defined CFDC can clearly reflect the varying process of winding deformation, which is helpful to effectively detect the winding condition for the secure and reliable operation of power transformer.

power transformer; winding condition; self-adaptive sifting empirical mode decomposition (EMD); central frequency distribution coefficient; vibration signal

TM471

A

10.13465/j.cnki.jvs.2017.19.016

國家自然科學基金(51207090)

2015-12-17 修改稿收到日期：2016-02-15

楊毅 男,碩士,工程師,1987年生