支承阻尼對多自由度齒輪系統非線性動力學的影響

向 玲，高雪媛，張力佳，賈 軼

(華北電力大學(保定) 機械工程系，河北 保定 071003)

支承阻尼對多自由度齒輪系統非線性動力學的影響

向 玲，高雪媛，張力佳，賈 軼

(華北電力大學(保定) 機械工程系，河北 保定 071003)

基于周期擴大法的思想，在考慮齒輪副間的時變嚙合剛度、齒側間隙、齒面摩擦等非線性因素的基礎上，建立了齒輪副的六自由度非線性動力學模型；采用數值積分方法求解系統響應，結合分岔圖、poincaré截面圖、FFT頻譜及最大李雅普諾夫指數圖(Largest Lyapunov Exponent,LLE)，系統地分析了支承阻尼對齒輪系統的影響。結果發現:支承阻尼的提高對系統的混沌吸引子和吸引域有著明顯影響，會使其逐漸減小，并使系統的混沌運動逐步退化穩定的周期運動，進而使系統的分岔特性變得更為復雜；隨著支承阻尼的提高，系統在徑向和扭轉方向的1/2次諧振幅度有所降低；支承阻尼對輪齒的嚙合的狀態有著重要影響，在一定轉速區可使系統發生雙邊沖擊到單邊沖擊的變化。

齒輪副；非線性動力學；摩擦；間隙；支承阻尼

齒輪系統是機械設備中廣泛用來傳遞動力的裝置，其動力學行為直接影響生產工作的精度、振動噪聲及設備壽命。Vaishya等[1-4]近年研究了多種因素對齒輪系統振動響應的影響。程歐等[5]研究了三自由度含多間隙的齒輪振動模型，發現系統在支承間隙較小而支承剛度較大時更加穩定。李應剛等[6]建立了外部動態激勵下直齒輪副的模型，發現增大激勵和阻尼比等參數，系統的振動響應能有效得到控制。張慧博等[7]提出了一種考慮徑向間隙與動態側隙耦合的齒輪轉子系統動力學模型。王樹國等[8]通過建立多間隙二級齒輪系統五自由度非線性振動模型，研究了轉速、阻尼比對系統分岔特性的影響。盛冬平等[9]建立了齒輪-轉子-軸承系統四自由度的彎扭耦合模型，分析了轉速、嚙合阻尼及齒側間隙等參數對系統分岔特性的影響。向玲等[10]采用周期擴大法確定了齒輪副的動力學模型，分析了支承剛度對系統分岔和混沌的影響。

基于以上研究可知，以往對于直齒輪副系統非線性動力學特性的研究多集中在低自由度模型，且多數文獻未考慮摩擦的作用；而支承阻尼又是影響齒輪-轉子系統非線性動力學特性的一個重要因素，但目前關于支承阻尼對系統響應影響的研究相對較少并且不全面，綜上所述，本文基于周期擴大法的思想[11]，綜合考慮齒面摩擦、時變嚙合剛度、齒側間隙和綜合嚙合誤差等非線性因素，建立了單級齒輪系統六自由度的動力學方程。運用數值仿真方法重點研究了支承阻尼參數對齒輪系統分叉特性、嚙合狀態的影響。

1 動力學模型

一對直齒輪副的非線性動力學模型如圖1所示。這里引入系統的六個自由度，即g0gggggg={θ1θ2xo1yo1xo2yo2}，圖中θ1、θ2為齒輪1、2的扭轉角位移；xo1、xo2為齒輪1、2的橫向位移；yo1、yo2為齒輪1、2的徑向位移。齒輪副的動態嚙合力可表示為

δ(t)=yo-yp+rb1θ1(t)-rb2θ2(t)-e(t)

(1)

式中:Fmeshi(i=1、2)為齒對i之間的嚙合力；khi(t) (i=1、2)為齒對i之間的時變嚙合剛度；chi(i=1、2)為齒對i之間的嚙合阻尼；δ(t)為齒輪副的動態傳遞誤差(Dynamic Transimission Error,DTE);e(t)為靜態傳動誤差;f(x)為具有分段線性特征的間隙非線性函數

(2)

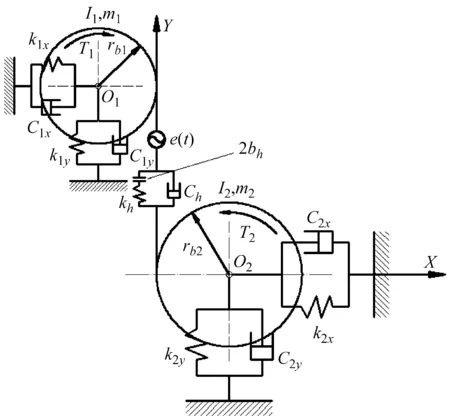
圖1 直齒輪副非線性動力學模型Fig.1 Nonlinear dynamic model of a spur gear pair

1.1時變嚙合剛度

直齒輪的重合度ε一般位于1～2，這就意味著齒輪在傳動時處于單雙齒交替嚙合狀態，如圖2(a)所示為一對齒的嚙合歷程，齒輪的單、雙齒區嚙合時間分別為t1、T0-t1，其中T0為一個法距對應的嚙合時間。周期擴大法的思想即為當一對齒嚙出時，假設繼續保持嚙合一個單齒區嚙合時間，但對應的嚙合剛度、摩擦因數等參數均為0，以一對齒的矩形波時變剛度模型[12-13]為例作說明，假設其擴大周期后的剛度曲線為kh2(t)，則另外一對參與嚙合齒的剛度kh1(t)可表示為kh2(t+T0)，輪齒的綜合剛度曲線可由兩齒對的剛度表示，如圖2(b)所示。可知其綜合剛度并未因周期的擴大而改變。圖中，k1，k2，kmax，kmin分別相關的剛度參數，文中為了進行長期地動力學分析，將單對齒的時變剛度kh2(t)擴展為以2T0為周期的傅里葉級數，則kh1(t)可由kh2(t)得到，兩者同取二次諧波項

(3)

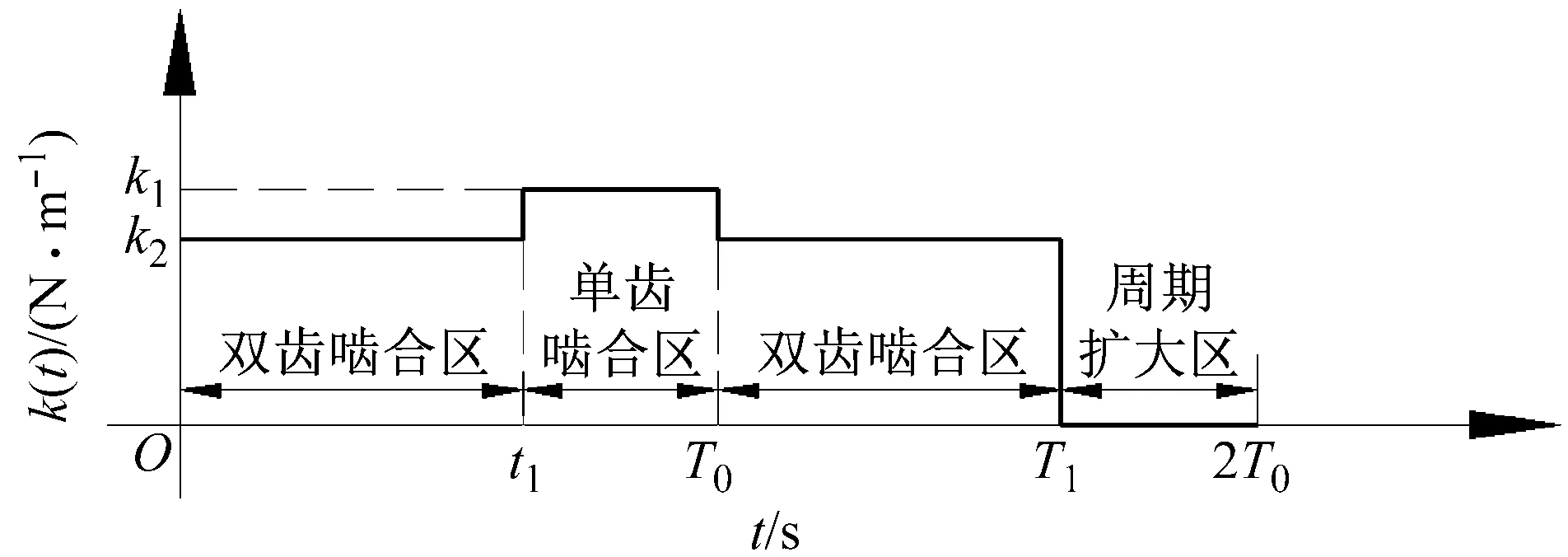
(a) 單雙齒時變剛度

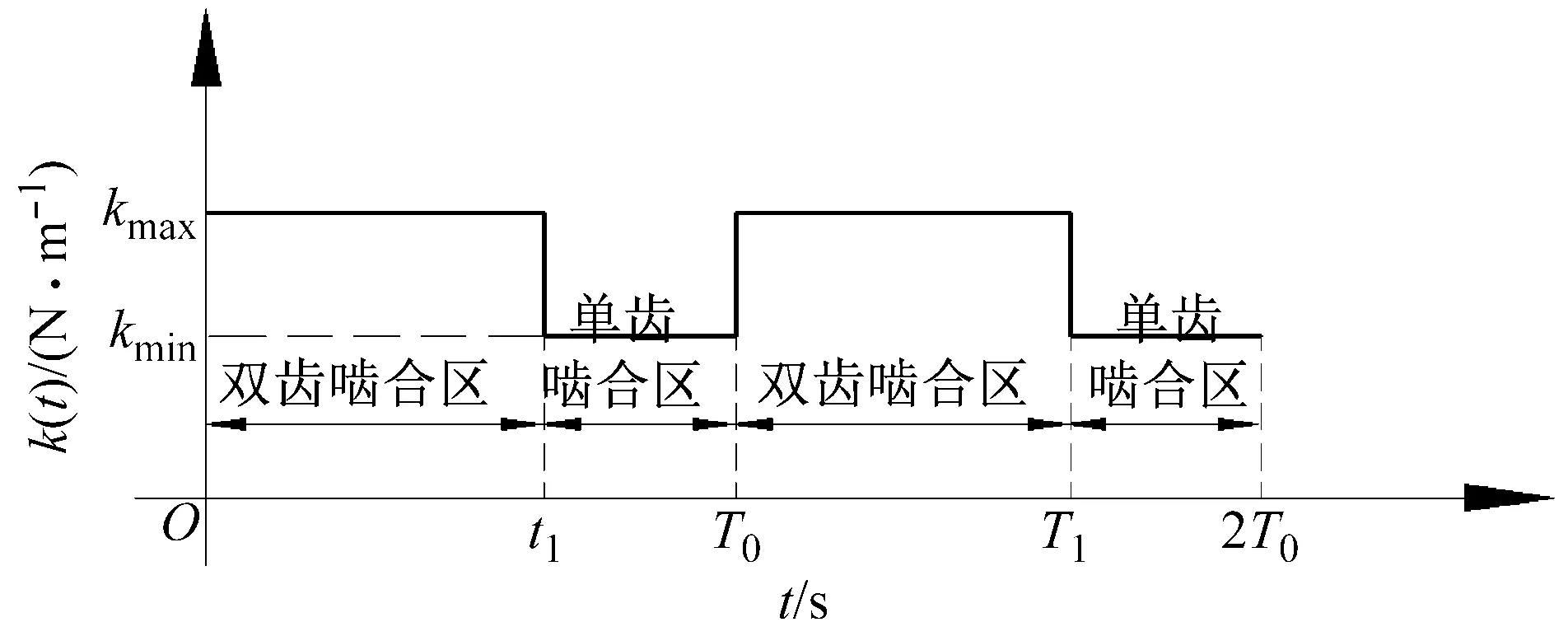
(b) 綜合時變剛度圖2 齒輪的時變嚙合剛度Fig.2 The time varying stiffness of gear pair

1.2齒面摩擦

對于一對嚙合齒，當嚙合點在節圓上部和下部時，由于齒面間的滑動速度改變方向，致使摩擦力的方向發生改變。根據庫倫摩擦定律，由式(1)可得到嚙合時各齒對之間的齒面摩擦力

(4)

式中:μi為齒面摩擦因數，其大小隨齒對的相對滑動速度的變化而周期性變化，但變化范圍不大；λi為擴大周期后的摩擦力方向系數。

(5)

摩擦力矩可由幾何關系推導得到，S1i，S2i(i=1,2)表示齒對i之間的摩擦力對齒輪1、齒輪2的力矩，rbi、rai分別為齒根圓、齒頂圓半徑；α為壓力角，ω1為主動輪角速度，Pb為基圓節距。

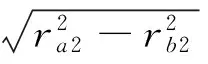
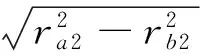
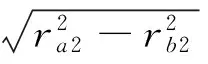
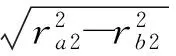
(6)

2 動力學方程的建立及量綱一化

由圖1所示模型可得到齒輪副的非線性動力學微分方程式(7)。

(7)

將式(7)中的前兩個方程合并，引入動態傳遞誤差δ(t)來表示，同時引入以下無量綱參數

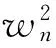
xo=x1·bn,yo=y1·bn,xp=x2·bn,yp=y2·bn,

ch1=ch2=ch,cn=ch/2Mewn,c1=c1x/ch,c2=c1y/ch,

c3=c2x/ch,c4=c2y/ch,k1=k1x/k0,k2=k1y/k0,

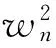
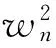
方程中的τ仍用t表示，則可得到量綱一化后的微分方程為式(8)。

(8)

式中:f1、f3為軸承的橫向預緊力，f2、f4為軸承的徑向預緊力；ξ1(t)、ξ2(t)均為周期函數，可由式(9)得到；ρ1(t)、ρ2(t)為摩擦力方向系數的函數。

(9)

無量綱化后的間隙性非線性函數可表示為

(10)

為進行動力學分析，對ζ1(t)，ζ2(t)，ρ1(t)、ρ2(t)展開成以2T0為周期的傅里葉級數，類似于式(3)對函數的傅里葉級數取二次諧波項進行動力學分析。還可推導得到量綱一化后的動態嚙合力為

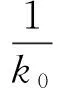
(11)

3 數值仿真與結果分析

采用4～5階變步長龍格庫塔法對式(8)表示的非線性系統進行數值求解，為消去瞬態響應，舍棄前2 000周期的結果。求解系統方程時如無說明均值均設置為0，設置求解的相對精度為RelTol=1×109、絕對精度為AbsTol=1×109。齒輪系統的主要參數如表1所示。

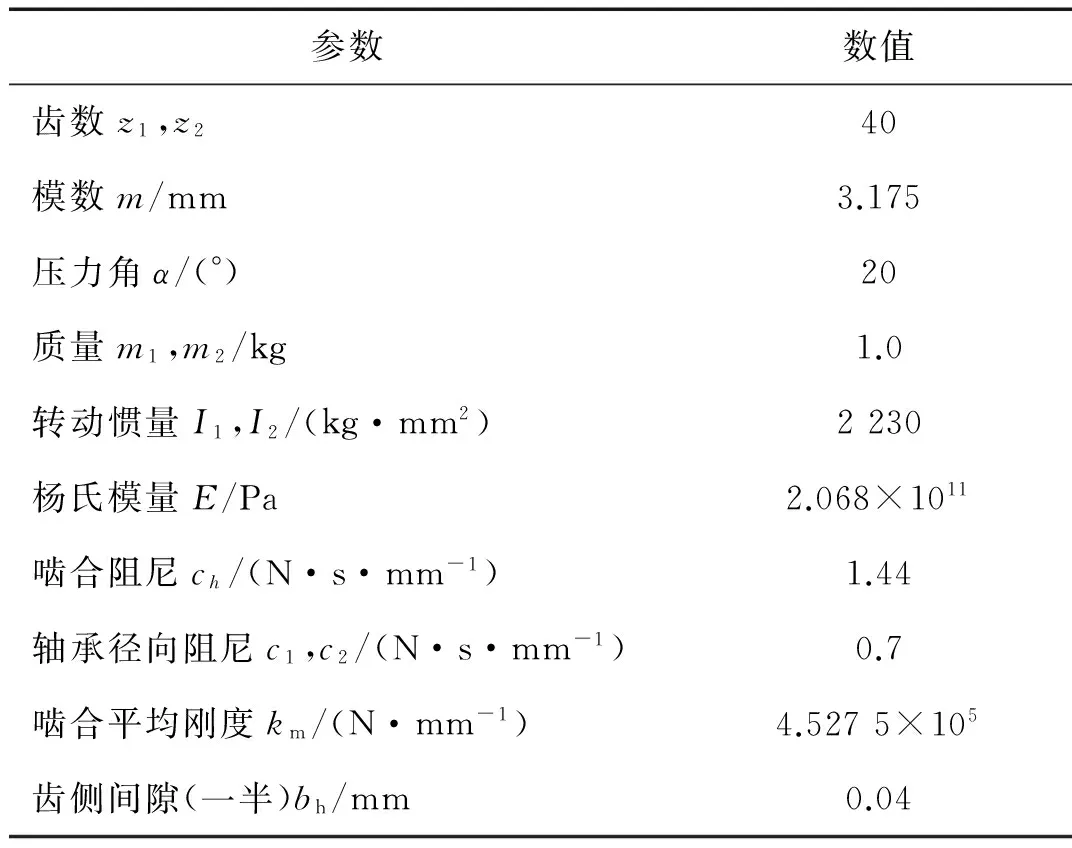
表1 齒輪系統的主要參數Tab.1 Main parameters of gear system

3.1支承阻尼對系統分岔特性的影響

為分析支承阻尼的影響，使用支承阻尼比ci(i=1,2,3,4)來表征支承阻尼的變化。取b=0.5，cn=0.03，通過改變ci來研究系統的變化規律。當ci=0.5時系統隨量綱一頻率ω變化時的分岔圖和最大Lyapunov指數曲線(Largest Lyapunov Exponent,LLE)如圖3所示。

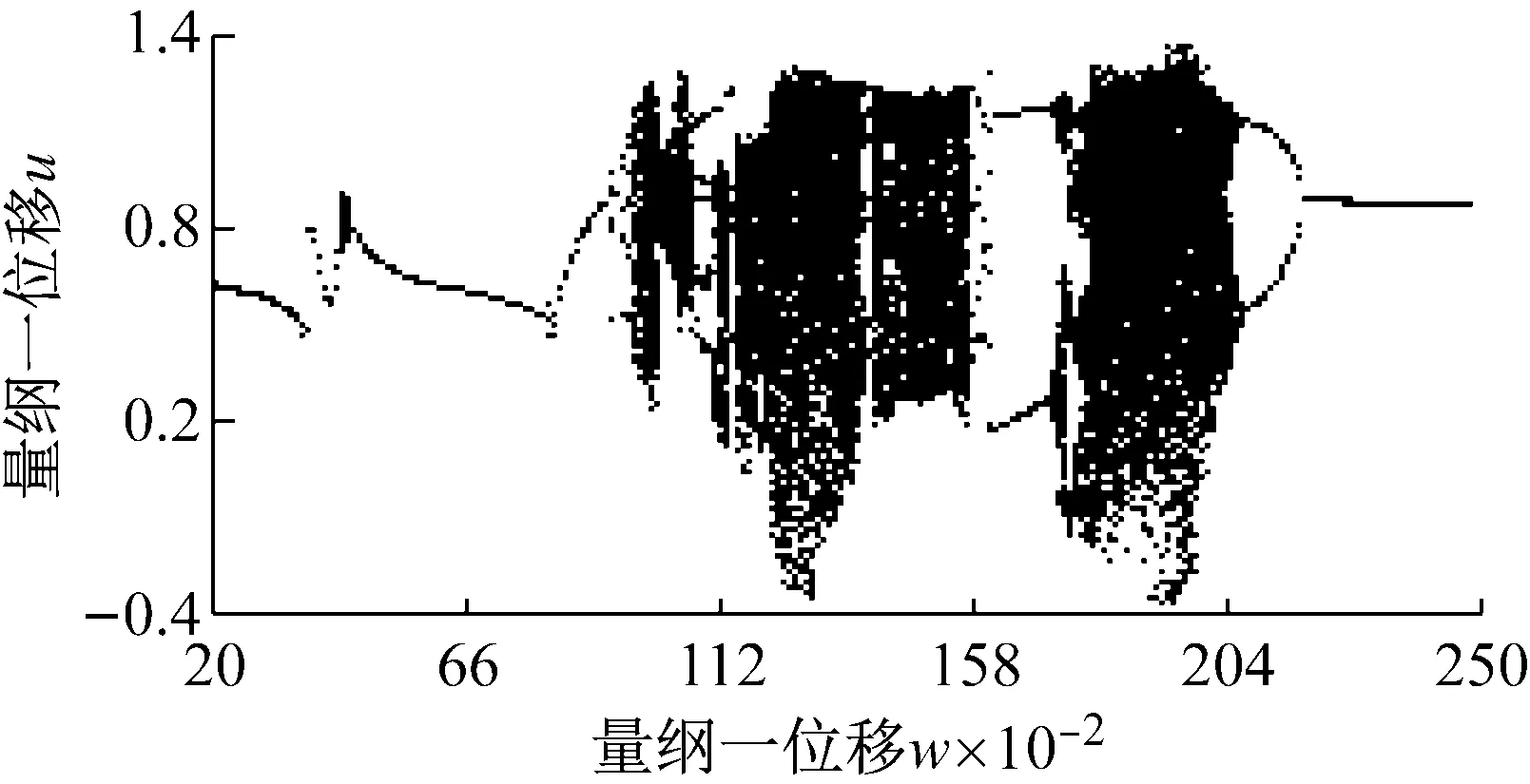
(a) 分岔圖

(b) LLE曲線圖3 ci=0.5時系統隨ω變化的分岔圖和LLE曲線Fig.3 The bifurcation diagram and LLE curve of the system with the change of ω when ci=0.5

整個激勵頻率區域，主要由兩個混沌區(LLE為正)和若干分隔的周期區(LLE為負)組成；兩混沌區域中有狹窄的周期區域。總體上，當激勵頻率逐漸增加時，系統響應由短周期運動經擬周期分岔進入混沌區1(ω=0.99-1.46)，后經擬周期倒分岔進入周期運動區域ω=1.46-1.76，同樣經擬周期分岔和倒分岔進入和離開混沌區2(ω=1.76-2.07)，隨后進入穩定短周期運動區域，相應的LLE指數值經歷了正、負、零的交替變化。

系統能量的損耗與阻尼有密切關系，而能耗的變化直接影響著系統振動響應的幅度及形態，為探究支承阻尼所對系統產生的影響，圖4、5分別給出ci=1.5和ci=2.0時系統隨無量綱頻率ω變化時的分岔圖和對應的LLE曲線曲線圖。對比以上各圖可知，在三種不同阻尼比情況下，激勵頻率區域均主要由兩個混沌區和間隔周期區組成；隨著支撐阻尼的增加，兩混沌區域逐漸有減小的趨勢，對應LLE正值區域減小；且混沌吸引子的大小和混沌的程度也逐漸減小，這點由LLE指數的大小變化也可以得知。另外，頻率區域ω=1.525-1.57的變化尤為明顯，隨著ci的提高，系統在該區域的響應整體上經歷了混沌-擬周期-周期的變化，相關的P截面、相圖及軸心軌跡的變化如圖6所示，說明了支撐阻尼的提高會使系統的混沌吸引子逐步退化穩定的周期吸引子，使系統運動的有序性加強。同時，隨著阻尼的提高，對應周期區域的LLE指數也逐漸減小，說明了阻尼對周期吸引子和吸引域存在著影響。

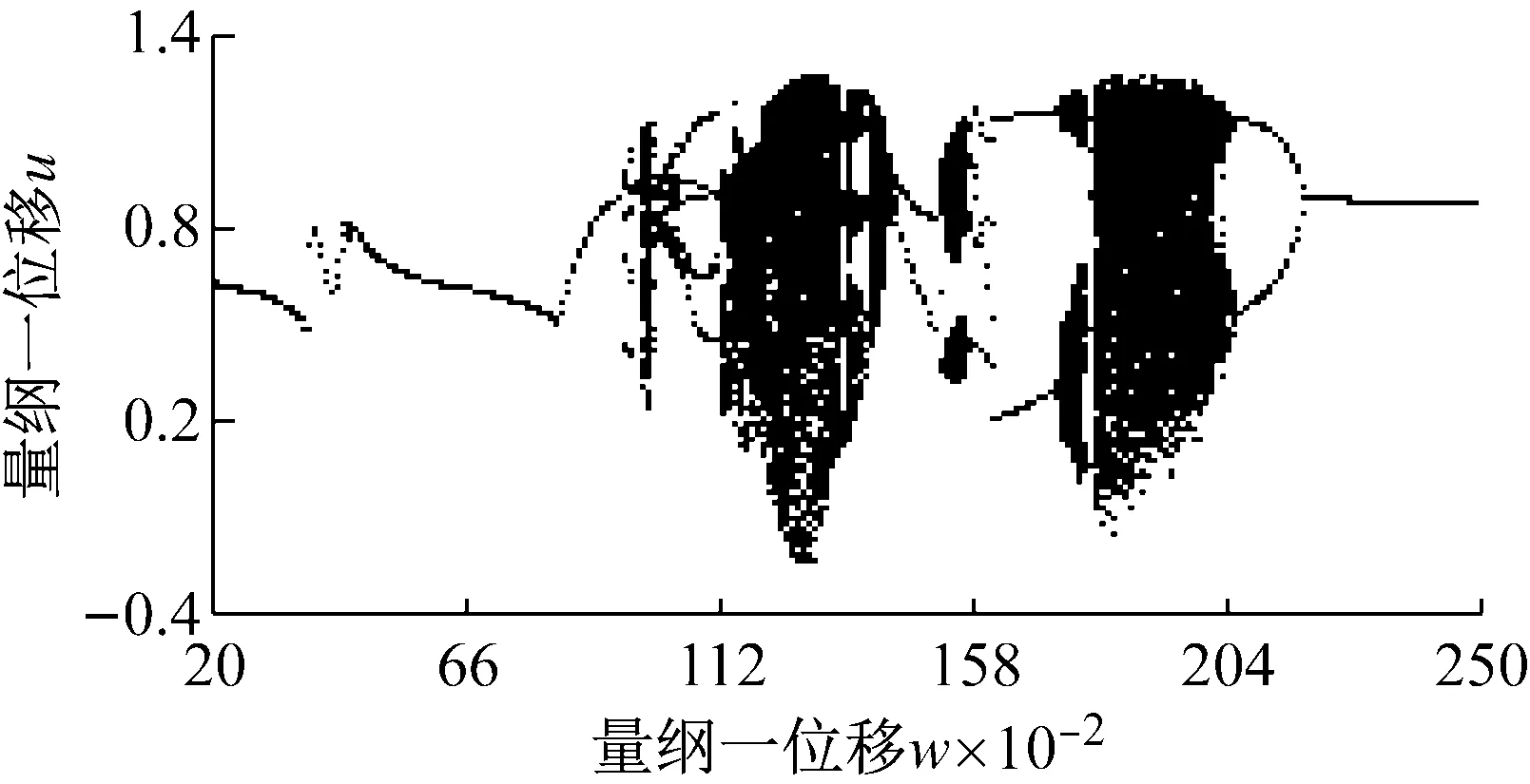
(a) 分岔圖

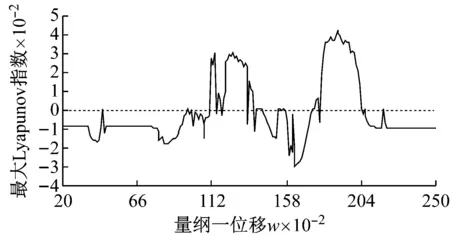
(b) LLE曲線圖4 ci=1.5時系統隨ω變化的分岔圖和LLE曲線Fig.4 The bifurcation diagram and LLE curve of the system with the change of ω when ci=1.5

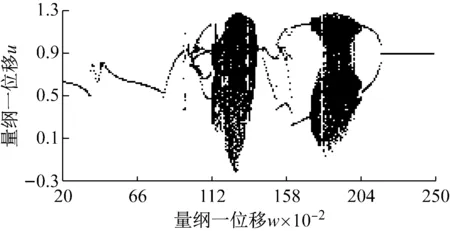
(a) 分岔圖

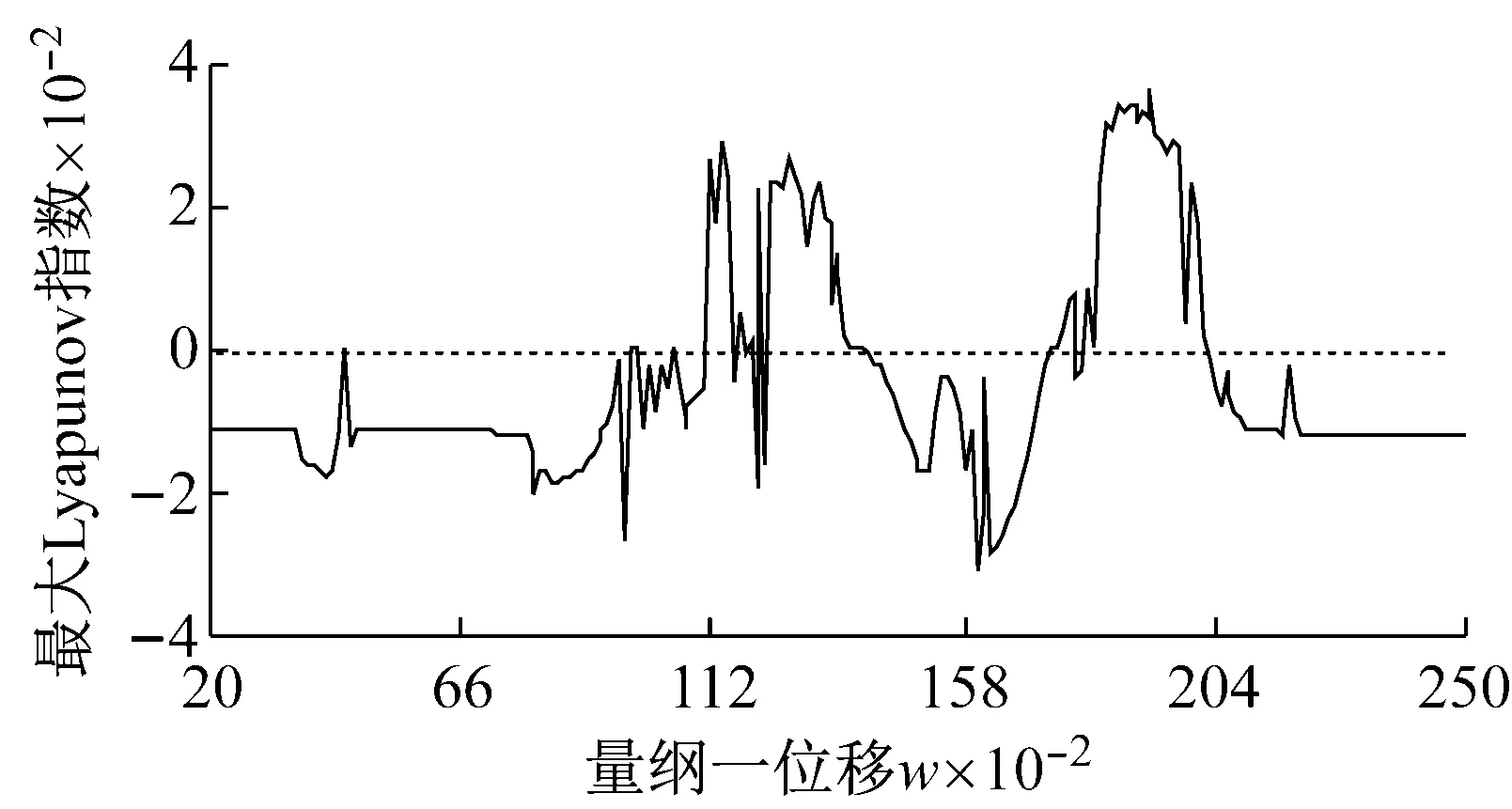
(b) LLE曲線圖5 ci=2.0時系統隨ω變化的分岔圖和LLE曲線Fig.5 The bifurcation diagram and LLE curve of the system with the change of ω when ci=2.0

3.2支承阻尼對嚙合狀態的影響

齒輪的嚙合狀態可由動態嚙合力DMF(Dynamic Meshing Force)的大小作為評估標準，DMF可由式(11)計算得到。這里記DMF最大值為Fmax，最小值記為Fmin，齒面沖擊可由Fmax的大小判斷，而齒背沖擊可由Fmin的大小及符號判斷。圖7所示為支承阻尼比ci分別為0.5、1.5和2.0時DMF的最大值和最小值曲線。對比圖中曲線可知，隨著支承阻尼的增加，在扭轉方向，1/2諧振頻率處的Fmax稍有減小，1/2諧振略有減弱；在低頻區，DMF隨阻尼變化不大，而在中高頻區，隨著ci的增加，Fmax和|Fmin|均有所減小；圖7(b)中，當ci=2.0時，系統在高頻區的|Fmin|基本為0，系統處于單邊沖擊狀態，而在ω=1.55～1.62和ω=1.78～2.02區域，ci=0.5時的|Fmin|基本大于0，此時系統處于雙邊沖擊嚙合狀態。兩圖說明了支承阻尼的提高會使系統的嚙合狀態發生大的變化，但其影響作用與系統的轉速有著密切關系。

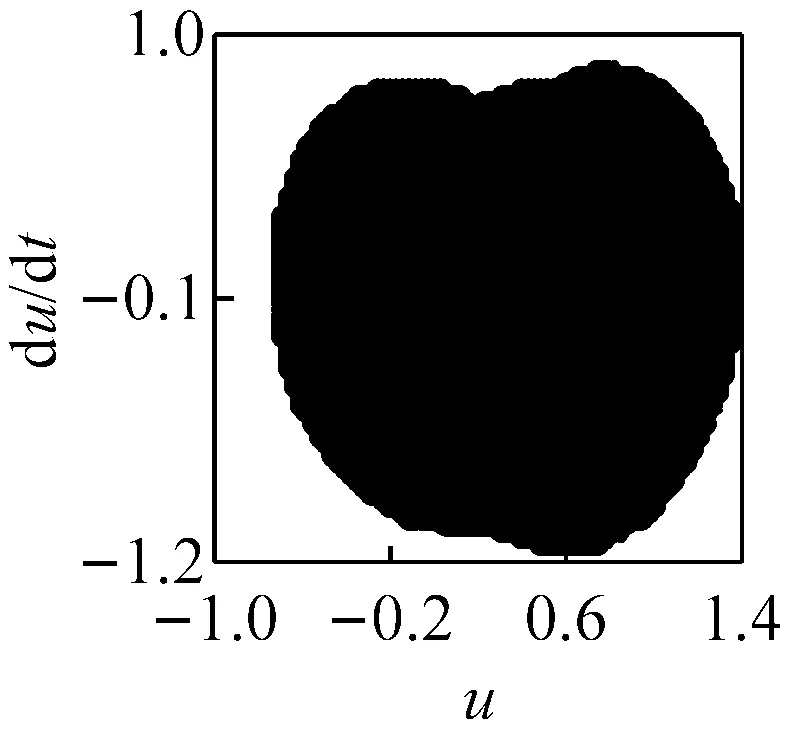
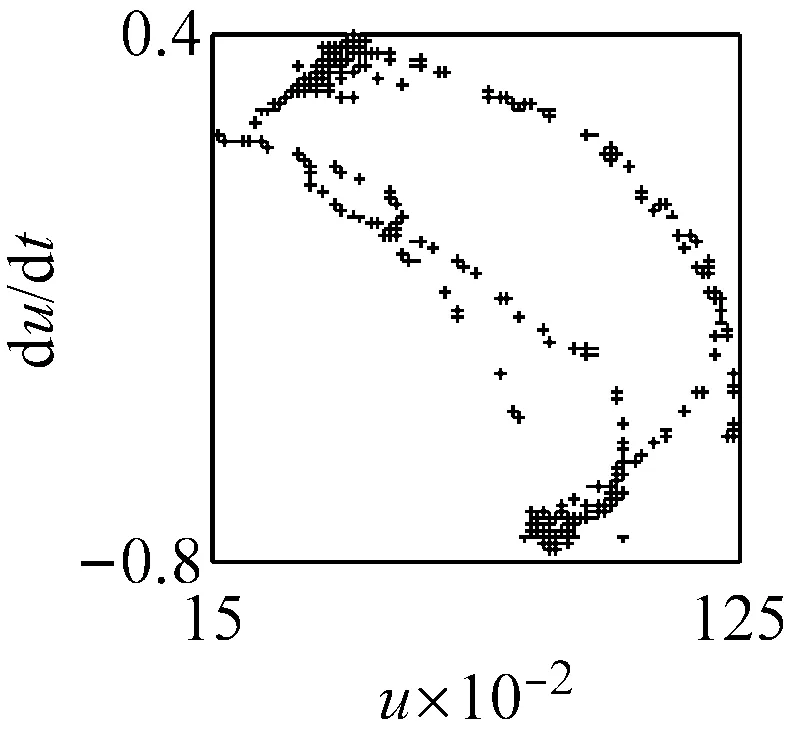
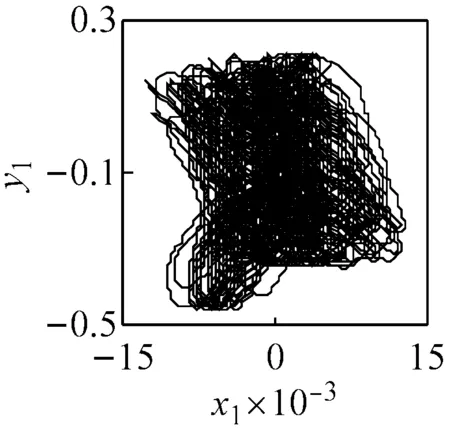
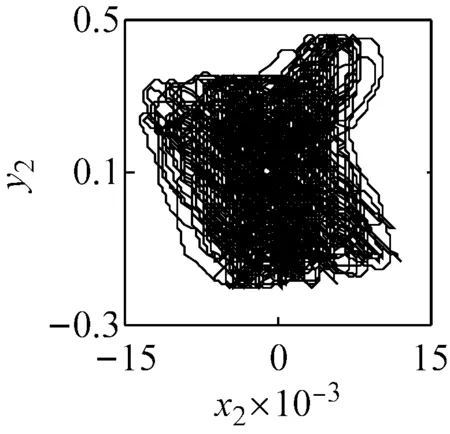
(a) ω=1.57, ci=0.5 (LLE=0.007 4)

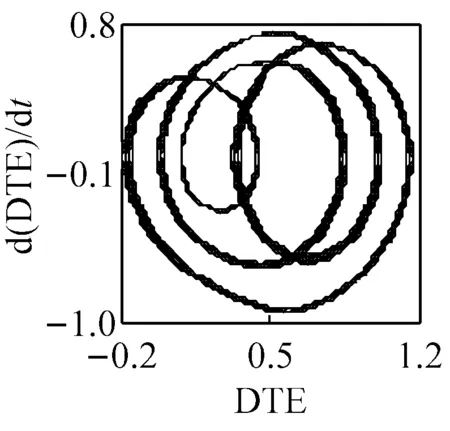
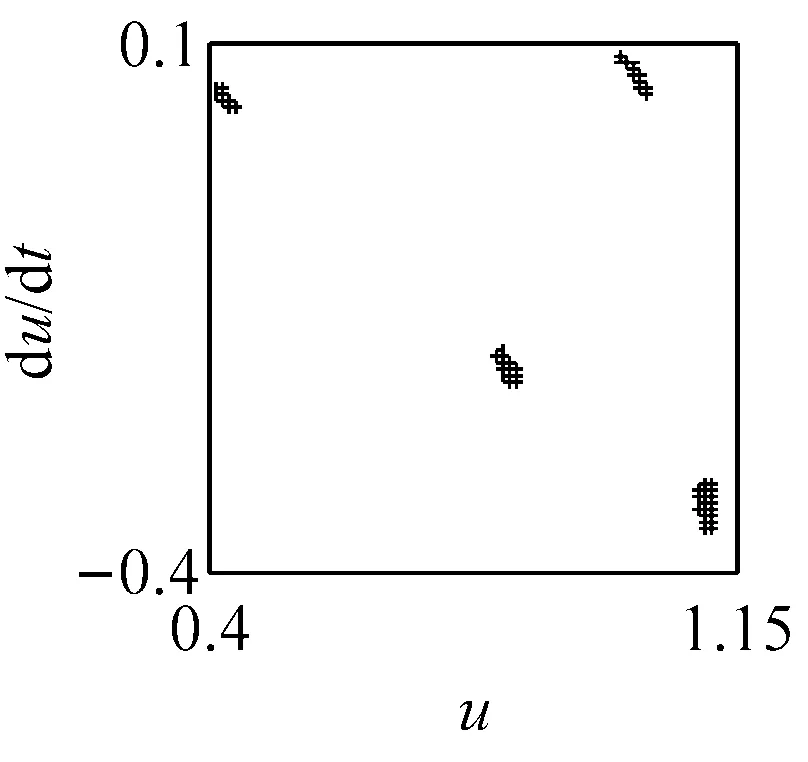
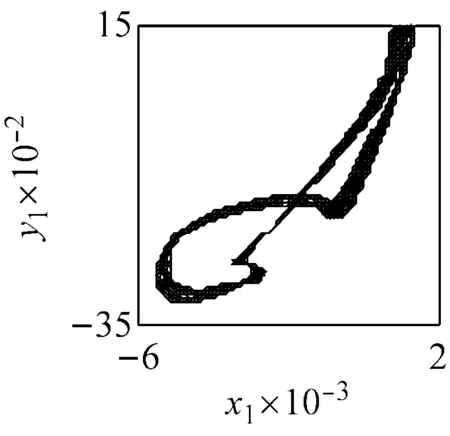
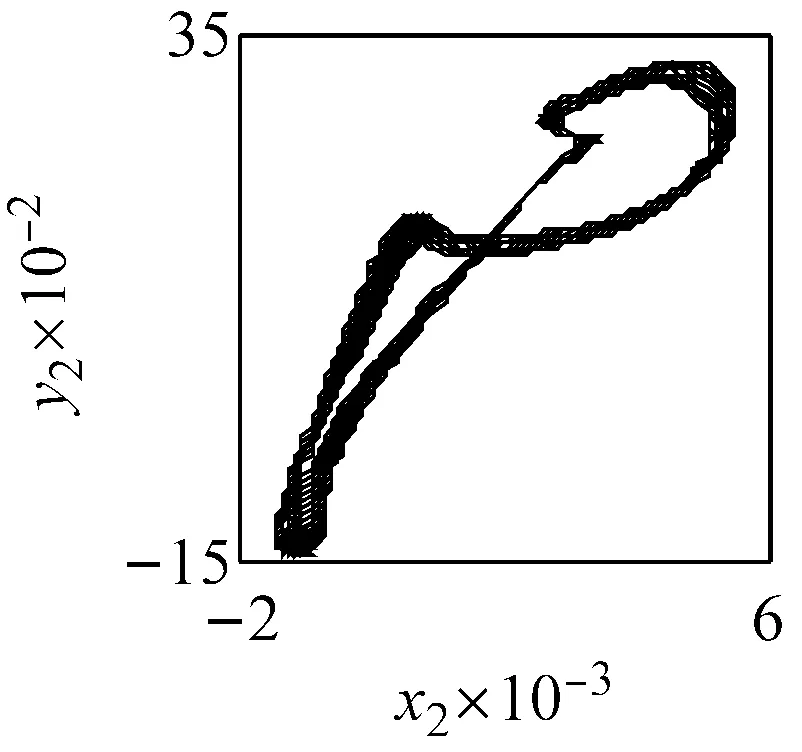
(b) ω=1.57, ci=1.5 (LLE=-0.000 16)

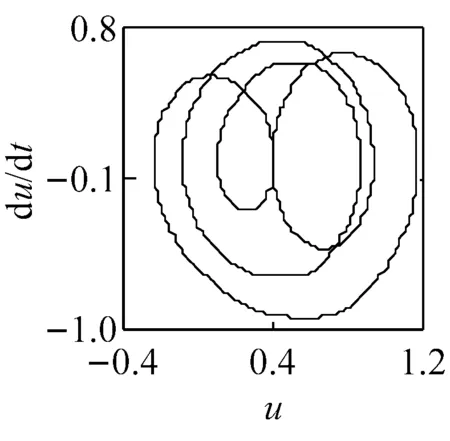
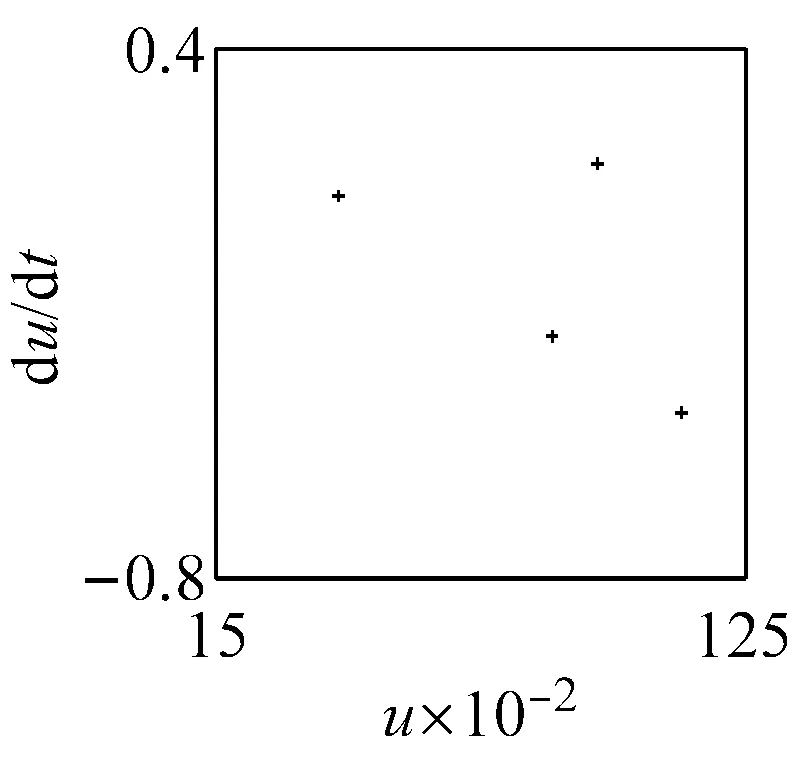
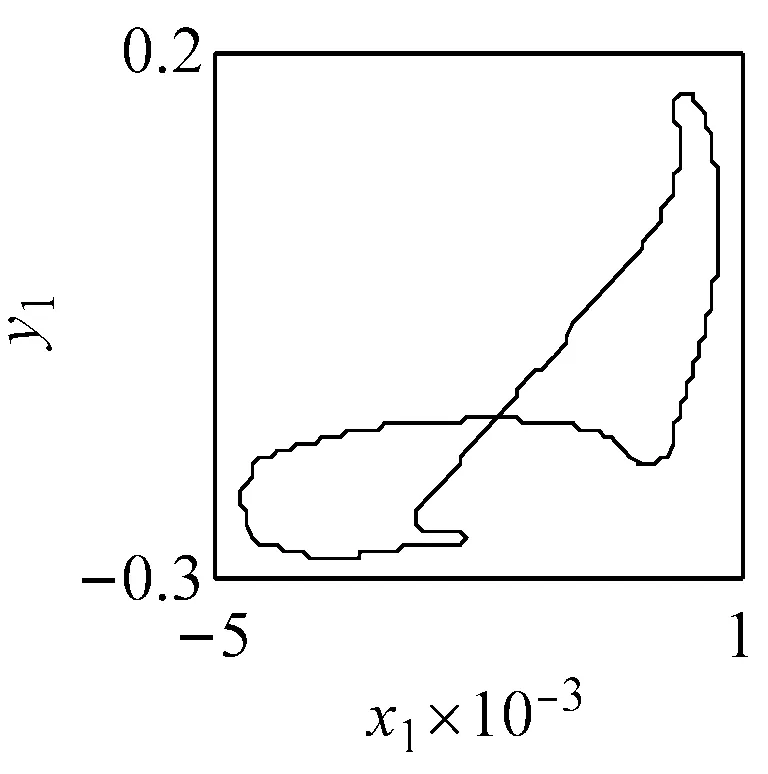
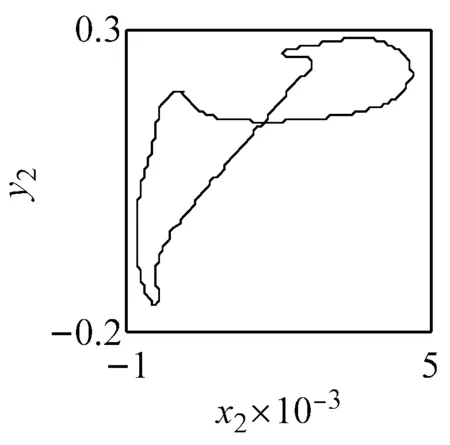
(c) ω=1.57, ci=2 (LLE=-0.008 9)圖6 主要頻率下系統響應的相圖、P截面及軸心軌跡圖Fig.6 The phase diagram, the P cross section and the axis trajectory of the system response within the main frequency

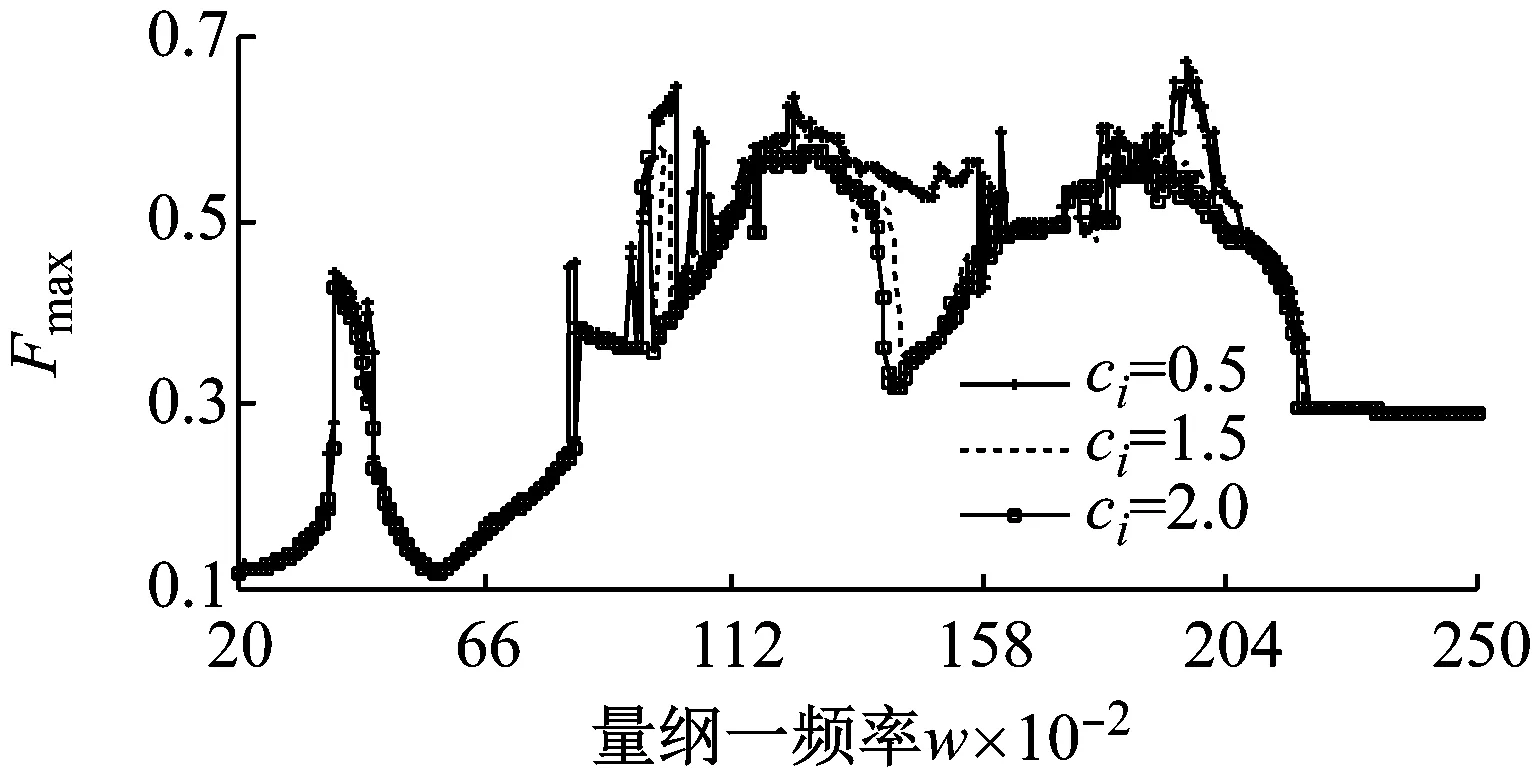
(a) 最大值曲線

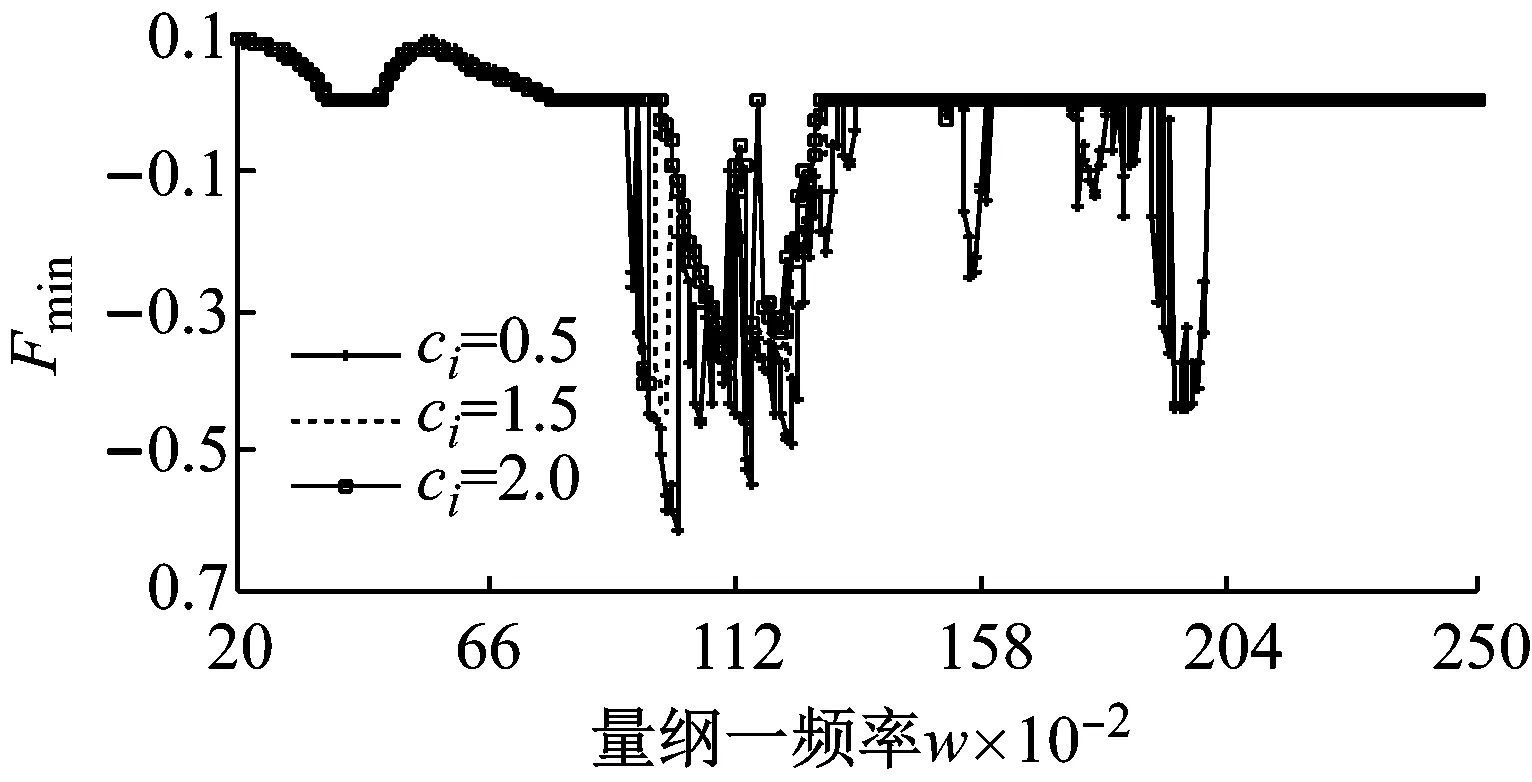
(b) 最小值曲線圖7 不同阻尼比下DMF隨ω變化的最大值曲線和最小值曲線Fig.7 The maximum and minimum curves of DMF with the change of ω under different damping ratio

4 結 論

根據周期擴大法的思想建立了考慮齒輪副間的時變嚙合剛度、齒側間隙、齒面摩擦等非線性因素的六自由度齒輪系統非線性動力學模型，用數值仿真方法研究了支承阻尼對齒輪系統非線性動力學的影響，得到以下結論：

(1) 在整個激勵頻率區域內，系統出現了單周期、擬周期、混沌等多種運動形式，并經多次跳躍由擬周期通道進入混沌運動。

(2) 支承阻尼的增加會使系統的混沌吸引子逐步退化穩定的周期吸引子，混沌區域逐漸有減小的趨勢，系統運動的有序性增強；同時，支承阻尼的增加會使對應周期域的LLE指數減小，影響周期吸引子和吸引域。

(3) 在低頻區，DMF隨支承阻尼變化不大，而在中高頻區，隨著ci的增加，Fmax和|Fmin|均有所減小；而支承阻尼的提高會影響齒輪系統的嚙合狀態，但其影響作用與激勵頻率有密切關系。

[1] VAISHYA M, SINGH R. Analysis of periodically varying gear mesh systems with coulomb friction using Floquet theory[J]. Journal of Sound and Vibration, 2001, 243(3)：525-545.

[2] MORADI H, SALARIEH H. Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity[J]. Mechanism & Machine Theory, 2012, 51(5):14-31.

[3] WANG J, ZHENG J, YANG A. An analytical study of bifurcation and chaos in a spur gear pair with sliding friction[J]. Procedia Engineering, 2012, 31(16):563-570.

[4] LI S, KAHRAMAN A. A tribo-dynamic model of a spur gear pair[J]. Journal of Sound & Vibration, 2013, 332(20):4963-4978.

[5] 程歐, 茍向鋒. 多自由度齒輪系統非線性動力學分析[J]. 噪聲與振動控制, 2015, 35(6):31-35.

CHENG Ou, GOU Xiangfeng. Nonlinear dynamics analysis of a multi-DOF gear system[J]. Noise and Vibration Control, 2015, 35(6):31-35.

[6] 李應剛, 陳天寧, 王小鵬,等. 外部動態激勵作用下齒輪系統非線性動力學特性[J]. 西安交通大學學報, 2014, 48(1):101-105.

LI Yinggang, CHEN Tianning, WANG Xiaopeng, et al. Non-linear dynamics of spur gear pair under external periodic excitation[J]. Journal of Xi’an Jiaotong University, 2014, 48(1):101-105.

[7] 張慧博, 王然, 陳子坤, 等. 考慮多間隙耦合關系的齒輪系統非線性動力學分析[J]. 振動與沖擊, 2015, 34(8):144-150.

ZHANG Huibo, WANG Ran, CHEN Zikun, et al. Nonlinear dynamic analysis of a gear-rotor system with coupled multi-clearance[J]. Journal of Vibration and Shock, 2015, 34(8):144-150.

[8] 王樹國, 張艷波, 劉文亮,等. 多間隙二級齒輪非線性振動分岔特性研究[J]. 應用數學和力學, 2016, 37(2)：173-181.

WANG Shuguo, ZHANG Yanbo, LIU Wenliang, et al. Nonlinear vibration bifurcation characteristics of multi-clearance 2-stage gear systems[J]. Applied Mathematics and Mechanics, 2016, 37(2):173-181.

[9] 盛冬平，朱如鵬，陸鳳霞,等. 多間隙彎扭耦合齒輪非線性振動的分岔特性研究[J]. 振動與沖擊, 2014，33(19)：116-122.

SHENG Dongping, ZHU Rupeng, LU Fengxia, et al. Bifurcation characteristics of bending torsional coupled gear nonlinear vibration with multi-clearance[J]. Journal of Vibration and Shock, 2014, 33(19):116-122.

[10] 向玲, 賈軼, 李媛媛, 等. 內外激勵作用下多自由度齒輪系統的非線性動力學特性[J]. 振動與沖擊, 2016, 35(13): 153-159.

XIANG Ling, JIA Yi, LI Yuanyuan, et al. Non-linear dynamic feature of multi-freedom gear system subjected to internal and external excitation[J]. Journal of Vibration and Shock, 2016, 35(13): 153-159.

[11] TANG J, CHEN S, ZHOU C. An improved nonlinear dynamic model of gear transmission[C]//ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Las Vegas: ASME, 2007: 577-583.

[12] GILL-JEONG C. Nonlinear behavior analysis of spur gear pairs with a one-way clutch[J]. Journal of Sound and Vibration, 2007, 304(Sup1/2):18-30.

[13] WALHA L, FAKHFAKH T, HADDAR M. Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation, bearing flexibility and backlash[J]. Mechanism & Machine Theory, 2009, 44(5):1058-1069.

Effectofsupportingdampingonthenonlineardynamicsofmulti-freedomgearsystems

XIANG Ling, GAO Xueyuan, ZHANG Lijia, JIA Yi

(Department of Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Based on the period-enlargement method, a six degrees of freedom nonlinear dynamic model with consideration of the rectangular-wave mesh stiffness, backlash, sliding friction and other nonlinear factors of a spur gear pair was established. The numerical integration method was applied to solve the responses of the system. The bifurcation diagrams, Poincaré maps, FFT spectrum and the largest Lyapunov exponents were used to systematically analyze the effect of supporting damping on the gear system. The results show that the chaotic attractor and chaotic domain would decrease gradually and even degenerate to stable periodic motion as the supporting damping is improved, resulting in the complexity of the bifurcation characteristic of the gear system. Moreover, the resonance of the system atω/2(ωis the exciting frequency) would be weakened. Finally, the supporting damping has an important effect on the meshing state of the gear system and could make the system exhibit a change from double-side impact motion to single-side impact motion.

gear pair; nonlinear dynamics; friction; backlash; supporting damping

TH113

A

10.13465/j.cnki.jvs.2017.19.021

國家自然科學基金資助項目(51475164);河北省自然科學基金(E2013502226)

2016-05-25 修改稿收到日期：2016-08-14

向玲 女，博士，教授，1971年4月生