考慮間隙的空間圓柱鉸多體系統運動學精度及動力學分析

劉太素，錢林方，尹 強

(南京理工大學 機械工程學院，南京 210094)

考慮間隙的空間圓柱鉸多體系統運動學精度及動力學分析

劉太素，錢林方，尹 強

(南京理工大學 機械工程學院，南京 210094)

為了研究空間圓柱鉸間隙對系統性能的影響，針對典型的空間圓柱間隙鉸結構，分析了其所有可能出現的接觸模式。針對空間圓柱鉸軸向和徑向都存在間隙的情況，對復雜的接觸模式進行了幾何和運動學分析，提出一種改進的計算潛在接觸點位置的方法，建立了接觸碰撞力模型，將其帶入多體系統動力學方程。對空間雙擺進行了理想模型和間隙模型的對比分析。結果表明，由于軸向和徑向間隙的存在，系統的運動學精度和動力學性能都受到了很大的影響，間隙大小的變化也會改變系統的運動學到位精度。空間圓柱間隙鉸的建模方法和結果為機械結構的設計和改進提供了理論依據。

空間圓柱鉸；接觸模式；鉸間隙；潛在接觸點；多體系統

在工程實際中，由于制造、裝配、磨損等原因，相對運動的鉸間并不是理想的，而是存在間隙，而這些間隙是不可忽略的，間隙的存在會對機械系統的運動學精度和動力學性能產生不容忽視的影響[1-4]。

文獻[5-6]分別對含有間隙的旋轉鉸和移動鉸進行了建模分析，得出了較為通用的模型。文獻[7-8]研究了柔性桿對機械系統性能的影響。文獻[9]同時考慮了鉸間間隙和桿的柔性，對平面四桿機構進行了運動學和動力學特性分析。文獻[10-11]在鉸間間隙加入潤滑模型，考慮了潤滑對系統動力學性能的影響。文獻[12-14]研究了多種因素對帶有鉸間間隙的機械結構的影響，包括間隙大小、摩擦因數、輸入速度等。

以上的研究都是針對平面問題進行開展，但是，在實際的機械系統在運動過程中，很多系統都是空間結構，而且有些平面系統在運動過程中也會由于角度誤差變成空間問題。因此，需要建立空間間隙鉸的合理模型。文獻[15]針對空間球鉸間隙進行了建模分析，利用一個四桿機構驗證了球鉸間隙對系統性能的影響。文獻[16-17]建立了空間圓柱鉸間隙的幾何和力學模型，并進行了運動學精度和動力學特性分析。文獻[18-19]利用有限單元法建立了鉸間隙模型，此模型既可以運用在平面鉸機構，又可以在空間鉸機構使用。然而，以上空間圓柱間隙鉸模型都只是考慮徑向間隙對系統的影響，而沒有考慮軸向間隙對結構的影響，也未考慮角度偏差的影響。基于以上原因，文獻[20]利用絕對坐標系法分析了圓柱鉸軸向間隙和徑向間隙對空間剛柔耦合多體系統的影響，結果表明，在實際的工程問題中，很多圓柱鉸結構中，軸向也會存在端蓋約束軸向運動，而且有些間隙的角度也不容忽視。因此，需要同時考慮軸向間隙和角度偏差對系統的影響。

在實際的圓柱鉸結構中，軸與軸套之間不僅會發生徑向接觸，而且在軸線方向也會存在接觸碰撞，三維結構如圖1所示。由于間隙的存在，軸與軸套之間不僅會相對移動，也會相對轉動，轉角的存在會使得接觸碰撞變的更加復雜。因此，針對典型的空間圓柱間隙鉸模型，本文首先對其接觸模式進行分析，得出了所有的接觸模式，然后通過對兩個體的幾何結構和運動情況進行分析，結合空間幾何與矢量計算，提出一種改進的計算潛在接觸點位置的方法，得到了潛在接觸點的位置以及接觸碰撞穿透量的計算公式，然后建立接觸碰撞力模型，最后，通過運動學分析和動力學分析得出空間圓柱鉸間間隙對系統運動學到位精度及其動力學性能的影響。

圖1 空間圓柱間隙鉸示意圖Fig.1 Schematic diagram of spatial cylindrical joint with clearances

1 空間圓柱間隙鉸幾何和運動描述

1.1空間圓柱間隙鉸接觸模式分析

如圖1所示為空間圓柱間隙鉸的典型結構，體1表示軸套，體2由中間的銷軸和兩端的端蓋組成，作為一個整體一起運動，體1與體2之間存在相對轉動和相對移動，在軸向和徑向都存在間隙，由于間隙的存在，體1和體2由約束狀態變為拓撲可變的結構，兩個體之間的運動變為兩種狀態，一種是自由運動狀態，一種是接觸狀態，兩個體都存在六個自由度，當兩個體相對運動時，體1和體2總是在自由狀態和接觸狀態之間切換。因此準確的分析體1與體2之間的接觸模式，是正確建立間隙接觸模型的基礎。

針對該典型空間圓柱間隙鉸結構，體1和體2之間存在多種接觸模式，分析可得體1和體2之間存在如下接觸模式：①自由狀態，體1和體2之間無接觸；②體2銷軸與體1的內表面單點接觸；③體2的端蓋與體1的端面單點接觸；④體2銷軸與體1內表面線接觸；⑤體2的端蓋與體1端面面接觸；⑥體2銷軸與體1內表面線接觸，同時體2端蓋與體1端面面接觸；⑦體2銷軸與體1內表面相反的兩個點接觸；⑧體2兩端端蓋各一個點與體1端面兩個點接觸；⑨體2銷軸上一個點與體1內表面接觸，同時體2端蓋一個點與體1端面接觸；⑩體2銷軸一個點，端蓋一個點與體1兩點接觸；體2銷軸兩個點，端蓋一個點與體1三點接觸；體2銷軸一個點，兩端端蓋各一個點與體1三點接觸，體2銷軸兩個點，兩端端蓋各一個點與體1四點接觸。以上共13種接觸模式，如圖2所示。

(a)(b)(c)(d)(e)(f)(g)(h)(i)(j)(k)(l)(m)

在相對運動過程中，根據幾何結構和運動狀態，以上接觸模式都有可能出現，或者在幾種接觸模式之間切換。對以上接觸模式進行分析，找出體1和體2的潛在接觸點，才能夠建立正確的接觸碰撞力模型。

1.2空間圓柱間隙鉸幾何和運動分析

首先建立全局坐標系和連體坐標系，如圖3所示。其中，O-XYZ為全局坐標系，O1-X1Y1Z1為體1的連體坐標系，O2-X2Y2Z2為體2的連體坐標系。在體1兩端面的圓心處建立兩個點J和K，在體2的銷軸兩端面圓心處建立兩個點C和D。R1和R2分別為體1軸套內圓半徑和外圓半徑，R3和R4分別為體2銷軸半徑和端蓋半徑，O1和O2分別為體1和體2的質心位置。

圖3 空間圓柱間隙鉸幾何結構及坐標系圖Fig.3 Geometry structure and coordinate system of spatial cylindrical joint with clearances

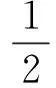
其中，LCD和LJK分別為銷軸長度和軸套長度。

綜合分析以上接觸模式，可以得出接觸碰撞總是發生在軸套的端面上，其中體1軸套與體2銷軸的接觸碰撞發生在軸套端面的內圓上，體1軸套與體2端蓋的接觸碰撞發生在體1軸套端面外圓上。在兩個體相對運動過程中，接觸模式最復雜的為如圖2中的最后一種，最后一種接觸模式中四個接觸對可能同時存在，也可能出現其中的某幾個接觸對，因此，對最后一種接觸模式進行分析，假設四個接觸對都可能發生，可以概括前面所有的接觸模式。

確定全局坐標系和局部坐標系后，點的坐標就可以分別在全局坐標系、局部坐標系1和局部坐標系2中表示，則點C和點J在全局坐標系中表示為

(1)

(2)

同理可得點D和點K在全局坐標系中表示為

(3)

(4)

當體1和體2發生相對運動時，局部坐標系也跟著體一起運動，兩個體之間存在四個潛在接觸對，如圖2(m)所示。設體2銷軸與體1軸套端面內圓的接觸點分別為點G和點H，體2端蓋與體1軸套端面外圓的接觸點分別為點P和Q，前視圖如圖4所示，假設體1相對靜止，體2相對體1運動，則點C和D在局部坐標系1中表示為

(5)

(6)

(7)

(8)

式中，B1為局部坐標系2對局部坐標系1的坐標變換矩陣。

圖4 潛在接觸點前視圖Fig.4 Front view of potential contact point

(9)

如圖1所示的兩個體在相對運動過程中，四個潛在接觸對都有可能發生，應分別對其進行分析，如下：

①當體2銷軸與體1軸套端面內圓左端接觸時，潛在接觸點為G，其左視圖如圖5所示。銷軸被軸套端面所截為一橢圓面，GF為橢圓的半長軸，由于直線GF與直線JK垂直，因此GF與CD之間的夾角為90°+θ，設點G所在的銷軸截面圓的圓心為OG，則OGG與CD垂直，所以OGG與GF之間的夾角為θ，可得

(10)

(11)

圖5 潛在接觸點左視圖Fig.5 Left view of potential contact point

(12)

(13)

(14)

由式(10)～式(12)可得點G在局部坐標系2中的局部坐標，從而得到點G在局部坐標系1中的坐標。

(15)

(16)

同理，可求得體2和體1右側接觸時的潛在接觸點H和Q，從而求得潛在接觸點H和Q處的穿透量δH和δQ。

確定接觸點的穿透量之后，接觸點的速度也就可以確定。對式(15)和式(16)求導，可得接觸點處的相對碰撞速度為

(17)

(18)

2 接觸碰撞力模型

2.1法向接觸碰撞力模型的確定

當兩個物體發生接觸時，可能會產生碰撞，碰撞過程會伴隨著能量損失，Herts接觸模型是常用的經典接觸模型，但該模型將兩個碰撞的物體假設為完全彈性碰撞，未考慮碰撞過程的能量損失，實際碰撞過程中，應該考慮相對碰撞速度、物體的幾何參數、物體的材料屬性等因素。因此，本文采用Lankarani-Nikravesh接觸力模型[21-22]，其公式為

(19)

剛度系數K可以表示為

(20)

阻尼系數C表示為

(21)

2.2鉸間摩擦力模型的確定

由于空間圓柱鉸間間隙的存在，使得鉸連接的兩個物體發生軸向的移動和繞軸的轉動，在運動過程中兩個相互接觸的物體表面是粗糙的，因此會發生相互摩擦，而且這種摩擦力是不可忽略的，對系統的性能也會產生影響。本文采用修正的Coulomb摩擦模型[23]來計算摩擦力，該模型能夠較準確的計算兩個物體在相對轉動和移動過程中的摩擦現象。切向摩擦力可以表示為

(22)

式中：cf為滑動摩擦因數;cd為動態修正系數;Fn為法向接觸碰撞力;vt為相對切向速度。

其中，動態修正系數cd可以表示為

(23)

式中,v0和v1是為計算動態校正系數而指定的速度值。

3 動力學模型描述

空間圓柱間隙鉸模型與空間圓柱理想鉸模型的不同之處在于約束問題，將理想鉸的運動學約束轉化為力的約束。因此需要將接觸力作為廣義外力引入動力學模型進行求解。

系統所受理想約束記為

Φ(q,t)=0

(24)

采用Lagrange乘子法對系統進行動力學建模如下[24]

(25)

式中：M為系統的質量矩陣;Φq為系統約束方程的雅克比矩陣;γ為加速度方程的右端項;g為系統所受的外力列陣;Fc是接觸力列陣，包含了接觸碰撞力和摩擦力;Mc為Fc相對于剛體質心的力矩;α，β是違約修正系數。

4 仿真和實驗分析

4.1鉸間間隙的存在對系統性能的影響

本文采用常用的空間雙擺模型來驗證上述模型的有效性和正確性，如圖6所示。雙擺模型由三個體組成，體1為基準座，與大地相對固定不動，體1上存在軸孔，體2為擺臂，與通過體1軸孔的銷軸和銷軸兩端的端蓋固定在一起，體3為擺臂，其中，體2與體1之間存在軸向和徑向的間隙，初始參數為體1軸半徑R3=50 mm，端蓋半徑R4=100 mm，體2孔內徑R1=50.1 mm，外徑R2=100 mm，軸長度L1=200.5 mm，孔長度L2=200 mm，徑向間隙為cx=cz=0.1 mm，軸向間隙兩端分別為cy=0.25 mm，軸向間隙和徑向間隙分別單獨考慮，當只考慮徑向間隙時，L1=200 mm，其余參數不變，當只考慮軸向參數時，R1=50 mm，其余參數不變。體3和體2之間假設為理想鉸，不存在間隙，違約修正系數α=1 000，β=1 414。

圖6 帶有圓柱鉸間隙的空間雙擺模型Fig.6 Spatial double pendulum with cylindrical clearance joint

初始時刻，雙擺放置在XZ平面，然后從該位置系統被釋放，僅在重力的作用下系統發生運動，雙擺的特征參數如表1所示。

表1 雙擺的特征參數Tab.1 Characteristic parameters of double pendulum

間隙的存在會對系統的運動學精度產生影響，由于L-N接觸力模型只能計算兩個接觸體之間的法向接觸力，且穿透量必須是沿接觸體之間的法線方向，因此，對軸向間隙和徑向間隙分別單獨考慮，圖7～圖9所示為帶有圓柱鉸徑向間隙的雙擺模型和理想鉸雙擺模型中體3在全局坐標系3個方向上的運動位置的變化的對比，此時，L1=L2=200 mm，即軸向無間隙。從圖中可以看出，當鉸間存在徑向間隙時，隨著運動時間的推移，物體的運動軌跡與理想軌跡發生了偏離，產生了運動誤差，但整體趨勢一致。剛開始曲線基本重合，表明間隙對系統的影響不大，但隨著時間的推移，間隙誤差的影響變大。此結果與文獻[16]的分析結果趨勢一致，從而驗證了本文方法的正確性。

圖7 體3質心X方向的位移Fig.7 Displacement of body 3’s center of mass in the X direction

圖8 體3質心Y方向的位移Fig.8 Displacement of body 3’s center of mass in the Y direction

圖9 體3質心Z方向的位移Fig.9 Displacement of body 3’s center of mass in the Z direction

圖10為當存在徑向間隙0.1 mm時，體3質心在全局坐標系Y方向的加速度隨時間的變化情況，從圖中可以看出，鉸間徑向間隙的存在會使得體3加速度發生劇烈的波動，說明徑向間隙會使得物體運動發生振動，不再平穩。

圖10 體3質心Y方向的加速度變化Fig.10 Acceleration change of body 3’s center of mass in the Y direction

由于體2相對體1不僅發生繞軸的轉動，還會發生沿軸的移動，而體2端蓋會與體1端面發生接觸碰撞，限制了相對的軸向運動。當只存在軸向間隙cy=0.25 mm時，R1=50 mm，即徑向無間隙，體2質心在軸向的運動如圖11所示，從圖中可以看出，在系統運動過程中，體2在軸向往復運動，在接觸時刻發生波動。

圖11 體2質心Z方向的位移Fig.11 Displacement of body 2’s center of mass in the Z direction

圖12～圖14為帶有空間圓柱間隙鉸的雙擺模型接觸碰撞力在全局坐標系中的變化情況。圖12和圖13為只考慮徑向間隙時的徑向接觸碰撞力，圖14為只考慮軸向間隙時的軸向接觸碰撞力。從圖中可以看出，銷軸徑向與軸孔的接觸碰撞力比較大，而軸向端蓋與軸孔端面的接觸碰撞力較小。由于間隙的存在，會產生軸向和徑向的接觸碰撞力，從而改變了系統的動力學性能，影響了系統的精度。

圖12 圓柱間隙鉸X方向接觸碰撞力Fig.12 The contact impact force of the cylindrical clearance joint in the X direction

圖13 圓柱間隙鉸Y方向接觸碰撞力Fig.13 The contact impact force of the cylindrical clearance joint in the Y direction

圖14 圓柱間隙鉸Z方向接觸碰撞力Fig.14 The contact impact force of the cylindrical clearance joint in the Z direction

4.2間隙大小對系統性能的影響

間隙的存在會對系統運動學精度及動力學性能產生影響，間隙大小的不同對系統的影響程度也會不同。圖15為當徑向間隙發生變化，而軸向不考慮間隙時，體3質心Y方向的位置變化情況，從圖中可以看出，間隙不同，末端體的運動軌跡變化很大，因此，需要合理控制鉸間間隙。

5 結 論

空間圓柱鉸間存在間隙會對系統運動學精度和動力學性能產生影響。本文針對工程實際中的空間圓柱鉸存在軸向間隙和徑向間隙的結構，首先對其接觸模式進行描述，分析所有可能出現的接觸模式，并運用矢量和空間幾何對模型進行了分析，提出一種改進的獲得潛在接觸點的方法，并計算得到接觸點處的穿透量。

圖15 不同間隙對運動精度的影響Fig.15 The effect for kinematics accuracy with different clearance size

采用動力學方程，結合Lankarani-Nikravesh接觸力模型和修正的Coulomb摩擦模型進行動力學建模，通過空間雙擺模型對模型進行了驗證，結果表明，與理想模型相比，間隙的存在會影響多體系統的位移，加速度等，軸向間隙的存在也會使得相對運動的物體發生往復碰撞而使得系統運動軌跡與理想情況發生偏離。由于間隙的原因，接觸表面會發生碰撞，產生較大的接觸碰撞力，也會對系統動力學性能產生影響。而且當間隙大小發生變化時，對系統的運動學精度和動力學性能的影響程度也不同。因此，需要合理控制鉸間間隙的大小，以提高系統的到位精度。

[1] DUBOWSKY S, FREUDENSTEIN F. Dynamic analysis of mechanical systems with clearances Part 1: formation of dynamic model[J]. Journal of Engineering for Industry，1971, 93(1): 305-309.

[2] RAVN P. A continuous analysis method for planar multibody systems with joint clearance[J]. Multibody System Dynamics，1998, 2(1): 1-24.

[3] FLORES P, AMBRSIO J, CLARO J C P, et al. Kinematics and dynamics of multibody systems with imperfect joints: models and case studies[J]. Lecture Notes in Applied and Computational Mechanics, 2008,34:169.

[4] MUVENGEI O, KIHIU J, IKUA B. Dynamic analysis of multi-body mechanical systems with imperfect kinematic joints: a literature survey and review[J]. Sustainable Research and Innovation Proceedings, 2011, 3:1-16.

[5] FLORES P, AMBROSIO J. Revolute joints with clearance in multibody systems[J] . Computers & Structures, 2004, 82(17/18/19): 1359-1369.

[6] FLORES P, AMBROSIO J, CLARO J C P, et al. Translational joints with clearance in rigid multibody systems[J] . Journal of Computational and Nonlinear Dynamics, 2008, 3(1):112-113.

[7] TIAN Q, ZHANG Y, CHEN L, et al. Simulation of planar flexible multibody systems with clearance and lubricated revolute joints[J]. Nonlinear Dynamics, 2010, 60(4): 489-511.

[8] LI J L, YAN S Z, GUO F, et al. Effects of damping, friction, gravity, and flexibility on the dynamic performance of a deployable mechanism with clearance[J]. Proceedings of Institution of Mechanical Engineers, 2013, 227(8): 1791-1803.

[9] ERKAYA S, UZMAY I. Modeling and simulation of joint clearance effects on mechanisms having rigid and flexible links[J]. Journal of Mechanical Science and Technology，2014, 28(8): 2979-2986.

[10] FLORES P, LANKARANI H M. Spatial rigid multi-body systems with lubricated spherical clearance joints: modeling and simulation[J]. Nonlinear Dynamics, 2010, 60(1/2): 99-114.

[11] MACHADO M, COSTA J, SEABRA E, et al. The effect of the lubricated revolute joint parameters and hydrodynamic force models on the dynamic response of planar multi-body systems[J]. Nonlinear Dynamics, 2012, 69(1/2): 635-654.

[12] FLORES P, AMBRSIO J, CLARO J C P, et al. Dynamic behaviour of planar rigid multi-body systems including revolute joints with clearance[J]. Proceedings of the Institution of Mechanical Engineers, 2007, 221(2): 161-174.

[13] FLORES P, LANKARANI H M. Dynamic response of multibody systems with multiple clearance joints[J]. Journal Computational and Nonlinear Dynamics, 2012, 7(3): 031003-031013.

[14] FLORES P. A parametric study on the dynamic response of planar multi-body systems with multiple clearance joints[J]. Nonlinear Dynamics, 2010, 61(4): 633-653.

[15] FLORES P, AMBROSIO J, CLARO J C P, et al. Dynamics of multibody systems with spherical clearance joints[J]. Journal of Computational and Nonlinear Dynamics, 2006, 1(3): 240-247.

[16] FLORES P, AMBROSIO J, CLARO J C P, et al. Spatial revolute joints with clearances for dynamic analysis of multi-body systems[J]. Proceedings of the Institution of Mechanical Engineers, 2006, 220(4): 257-271.

[17] 尉立肖，劉才山． 圓柱鉸間隙運動學分析及動力學仿真 [J]. 北京大學學報(自然科學版), 2005, 41(5): 679-687.

YU Lixiao, LIU Caishan. Dynamic simulation and kinetic description of revolute joint with spatial clearance [J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2005, 41(5): 679-687.

[18] BAUCHAU O A, RODRIGUEZ J. Modeling of joints with clearance in flexible multi-body systems[J]. International Journal of Solids & Structures，2002, 39(1): 41-63.

[19] BAUCHAU O A, JU C. Modeling friction phenomena in flexible multi-body dynamics[J]. Computer Methods in Applied Mechanics & Engineering, 2006,195(50/51):6909-6924.

[20] LIU C, TIAN Q, HU H. Dynamics and control of a spatial rigid-flexible multibody system with multiple cylindrical clearance joints [J]. Mechanism and Machine Theory, 2012, 52:106-129.

[21] LANKARANI H M, NIKRAVESH P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990, 112(3): 369-376.

[22] LANKARANI H M, NIKRAVESH P E. Continuous contact force models for impact analysis in multibody systems[J]. Nonlinear Dynamics, 1994, 5(2): 193-207.

[23] AMBROSIO J A C, SCHIEHLEN W, VALSEK M. Impact of rigid and flexible multibody systems: deformation description and contact models, in virtual nonlinear multibody systems[M]．Berlin: Springer Netherlands，2003: 57-81.

[24] 趙剛練，姜毅，郝繼光，等． 考慮圓柱鉸鏈間隙的多剛體系統動力學計算方法[J]． 振動與沖擊學報，2013，32(17):171-176．

ZHAO Ganglian，JIANG Yi，HAO Jiguang，et al．Computational method of rigid multibody system dynamics considering cylindrical joint clearance [J]． Journal of Vibration and Shock，2013，32(17): 171-176．

Kinematicsaccuracyanddynamicanalysisofmulti-bodysystemswithspatialcylindricalclearancejoints

LIU Taisu, QIAN Linfang, YIN Qiang

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

In order to investigate the influence of spatial cylindrical joints with clearances on system performances, all possible contact modes of a typical spatial cylindrical clearance joint were analyzed. Aiming at the spatial cylindrical joints with clearances in the axial and radial directions, the geometry and kinematics of complicated contact modes were analyzed. An improved method for computing potential contact points was proposed. The normal contact impact force model and the tangential friction force model were set up. Then, the multi-body dynamic equation was given with consideration of the normal contact impact force and the tangential friction force. Finally, a spatial double pendulum with joint clearance was taken as an example and the results were compared with those by using the ideal model. The results show that the kinematic accuracy and dynamic performance of the system were affected greatly, because of the existing clearances in the axial and radial directions, and different clearance sizes can change the kinematic accuracy of the system. The method and the results provide a theoretical basis for the design and improvement of the mechanical structures.

spatial cylindrical joint; contact mode; joint clearance; potential contact point; multi-body system

TH112

A

10.13465/j.cnki.jvs.2017.19.023

江蘇省自然科學基金(BK20140773)

2016-03-08 修改稿收到日期：2016-08-03

劉太素 男，博士生，1990年4月生

錢林方 男，博士,教授，1961年12月生