基于波函數法的自由阻尼薄板與聲學耦合響應

夏小均，徐中明，賴詩洋，張志飛, 賀巖松

(1.重慶大學 機械傳動國家重點實驗室,重慶 400030；2.重慶大學 汽車工程學院,重慶 400030;3.重慶工程職業技術學院 機械工程學院,重慶 402260)

基于波函數法的自由阻尼薄板與聲學耦合響應

夏小均1,2，徐中明1,2，賴詩洋3，張志飛1,2, 賀巖松1,2

(1.重慶大學 機械傳動國家重點實驗室,重慶 400030；2.重慶大學 汽車工程學院,重慶 400030;3.重慶工程職業技術學院 機械工程學院,重慶 402260)

對敷設自由阻尼薄板振動響應進行了分析，以復剛度為基礎得到了在Kirchhoff理論下復合薄板振動控制方程。基于波函數法理論，推導了自由阻尼薄板振動分析模型以及包含自由阻尼結構與聲腔的三維耦合模型的建模方法;以四邊固支自由阻尼矩形板及耦合的結構聲學系統為例，分別以波函數法與有限元法計算了其50～500 Hz頻段內的結構與聲學響應。結果表明：波函數法能有效的應用于添加自由阻尼的薄板振動以及結構聲耦合系統響應的預測與分析;相比于有限元法，其高精度、高收斂率的特點使波函數能有效解決更高頻率的聲振問題。

自由阻尼；波函數法；彎曲振動；結構聲耦合

隨著計算機輔助工程CAE(Computer Aided Engineering)技術更廣泛的運用和對現在有數值分析手段的深入研究，研究者發現廣泛應用的基于單元的方法如有限元法、邊界元法，由于插值誤差與污染誤差的存在，其只能應對較低頻率問題。而基于模態重疊率假設的統計類方法如統計能量法只對高頻問題有效[1-3]。因此，20世紀末出現的“中頻危機”使得人們努力地探尋針對中頻問題的數值分析方法和手段。當下代表性研究主要有：波有限元法(Wave Finite Element Method,WFEM)[4]，統計能量分布法(Statistical Modal Energy Distribution Analysis,SMEDA)[5]，復包絡向量(Complex Envelope Vectorization,CEV)[6]，復射線變分理論(Variational Theory of Complex Rays,VTCR)[7], 混合有限元-統計能量法(Hybrid Finite Element/Statistical Energy Analysis Method,Hybrid FE-SEA)[8],能量分析布法(Energy Distribution Analysis,EDA)[9],以及波函數法(Wave Based Method,WBM)[10]。其中Hybrid FE-SEA已經應用在一些商用軟件上，指導了很多工程研究，但該種方法的結果仍是時間或空間上的平均，且在仍存在一些理論待完善。而本文要討論的波函數則是完全不同現有基于單元法的確定性數值分析方法。

到目前，波函數法已經成功運用到了平板彎曲振動、薄膜振動、結構聲學耦合響應[11-13]、多孔阻尼材料聲學耦合響應[14]等問題。國內Peng等[16-17]對基于薄板彎曲振動以及二維的結構聲耦合問題也進行過相應研究。通過對該類常見聲振問題的預測分析，波函數法展現出了高效高精度的特點，使其能有效的運用于中頻振動與聲學問題。而在振動特性明顯的薄板類結構上敷設阻尼，業已成為工程中最常見的減振降噪手段，雖然基于單元法對自由阻尼結構的也有相關研究[18]，但如上文所述，該類方法分析中頻問題往往要求付出巨大的時間成本與精度妥協。因此，研究以如波函數法等高效的數值方法分析含有自由阻尼的結構振動與聲學響應問題，實現該類系統的中頻聲振預測具有實際的研究意義與工程價值。

文章在完成自由阻尼薄板振動分析的基礎上，結合波函數法理論完成該類結構的彎曲振動響應預測及其與聲腔耦合系統的聲學響應分析。并通過數值算例，驗證了方法的有效性，同時也再次體現了波函數法在針對中頻聲振問題的高精度與高收斂特性。

1 自由阻尼薄板振動響應

對于添加均勻厚度自由阻尼的薄板如圖1所示。結構層厚度為t1,阻尼層厚度為t2。

圖1 自由阻尼薄板截面示意圖Fig.1 Section of unconstraned damped plate

彎曲剛度為薄板類結構振動響應的關鍵，本次將敷設阻尼后構建虛擬約束阻尼結構，通過截面彎矩平衡求得帶約束層的彎曲剛度，通過消去約束層以及剪切變形的作用后得到自由阻尼薄板的彎曲復剛度B*[19]

(1)

對于含有自由阻尼的薄板，以經典的Kirchhoff理論來描述其彎曲振動。復合薄板振動方程

(2)

對于穩態振動響應，其位移可表達為wt(xs,ys)=wz(xs,ys)ejωt，而在外部激勵為Qt=Qejωt時，含有自由阻尼薄板的穩態振動響應控制方程表示為

(3)

2 結構聲學耦合穩態響應

對于含自由阻尼和薄板聲腔耦合系統，由于受到耦合聲壓面作用，復合薄板的振動響應方程修正為

(4)

而聲學域仍滿足Helmholtz波動方程

(5)

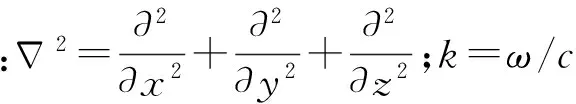
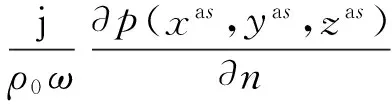
(6)

3 波函數法理論與實現

波函數法作為基于間接Trefftz方法，與現有基于單元的方法不同。其將分析域變量表示為嚴格滿足控制方程的一系列波函數的疊加。再通過如Galerkin等加權余量法實現邊界殘差積分歸零，來求得各波函數的權系數，進而得到求解響應。

3.1含自由阻尼薄板的彎曲振動響應

根據波函數法理論，薄板的彎曲振動響應表示為一系列結構波函數的疊加

(7)

結構波函數為

Ψs=e-j(kxsxs+kysys)

(8)

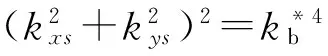
式中:Lxs,Lys分別為薄板外輪廓尺寸;j2=-1;s1=0,1,2,…,ns1;s2=0,1,2,…,ns2,ns=4(ns1+1)+4(ns2+1)波函數數量也即為模型的自由度。而對于外部點激勵定義為

(9)

對于各波函數權系數的計算，采取類似有限元中加遼金法等邊界加權余量法，將邊界誤差最小化為0，經整理得到計算各權系數Ws的系統矩陣

[Ass]{Ws}={fs}

(10)

其中,

(11)

(12)

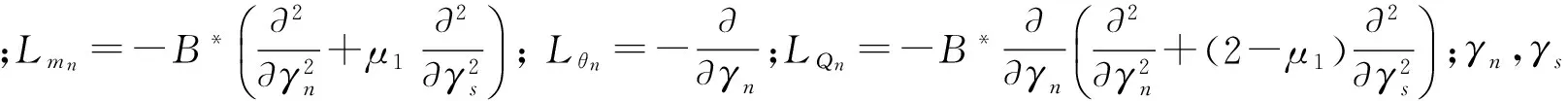
3.2結構聲耦合系統

同樣，對于聲學響應，也可表示為一系列的聲學波函數的疊加

φi≈[Φ]{ga}

(13)

式中:ga為未知的權系數;Φ為滿足Helmholtz控制方程的波函數，定義為

Φ=e-j(kxax+kyay+kzaz)

(14)

由于結構與聲腔的耦合作用，在接合面引入聲學波函數附加作用的函數

(15)

式中,Ωs為結構與聲域耦合邊界。因此結構位移表示式相應變換為

(16)

(17)

其中,

(18)

(19)

(20)

4 數值驗證

對于上述基于波函數法對含有自由層結構的聲振分析方法，以下通過兩個例子進驗證。一個為敷設自由阻尼薄板的彎曲振動響應分析，另一個為含有自由阻尼薄板與聲腔耦合系統的聲學響應。

4.1含自由阻尼矩形薄板

如圖2所示尺寸的四邊固支的薄板結構。引入的薄板為0.5 mm的鋁板，在其表面添加1 mm厚的阻尼層，兩種材料的參數如表1所示。在點(0.2 m，0.3 m)位置處施加一個法向的單位力，R點為選取的頻響觀測點，其平面坐標為(0.44 m，0.11 m)

圖2 自由阻尼薄板Fig.2 Geometry of unconstrained plate

表1 復合板材料參數Tab.1 Material parameters of plate and damp

波函數法通過Matlab2016a平臺編程實現，而有限元模型則在MSC/Nastran建立。為揭示有限元的特征以及其在更高頻率的限制，建立了精細和普通單元尺寸的有限元模型加以對比分析。其中精細有限元模型包含了60 000個四邊形單元與60 000個六面體單元，而普通單元尺寸有限元模型包含2 400個四邊形單元與2 400個六面體單元。取240 Hz時薄板的法向振動響應結果如圖3所示。波函數的計算結果與有限元符合較好。同時為了在頻域上對比兩種方法，選取了響應點在50～500 Hz段的響應。圖4為響應的實部，圖5為響應的虛部。結果同樣表明，在整個分析頻段內，波函數法的計算結果與精細建模的結果吻合較好，而單元尺寸較大的模型則在較多頻段出現較大差別，特別是在頻率較高的，其偏移更加明顯。而未敷設阻尼的薄板振動響應結果如圖6所示，薄板受其本身特征頻率影響，在很多頻率下的出現很大響應，也說明了阻尼的在抑制其振動的效果十分明顯。有無阻尼材料模型的計算結果都驗證了波函數法對預測自由阻尼薄板的振動響應的有效性。

(a) WBM

(b) FEM圖3 薄板在240 Hz法向振動位移響應的等高線圖Fig.3 Displacement response contour of damped plate at 240 Hz

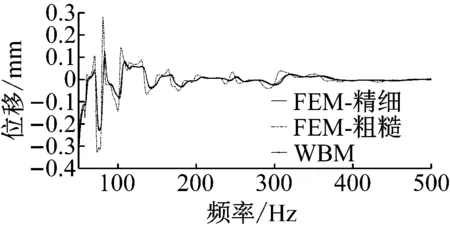
圖4 含阻尼薄板的振動位移頻響曲線(實部)Fig.4 Response plot of reference point with damp (real part)

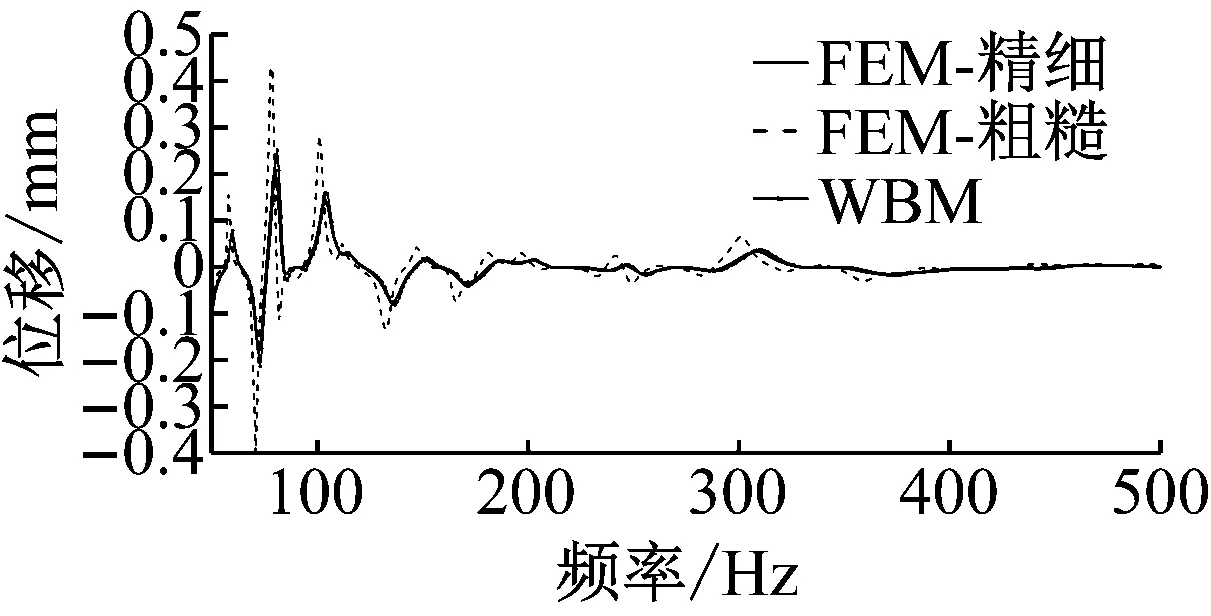
圖5 含阻尼薄板的振動位移頻響曲線(虛部)Fig.5 Response plot of reference point with damp (imaginary part)

圖6 無阻尼薄板的振動位移響應(實部)Fig.6 Response plot of reference point without damp (real part)

4.2含自由阻尼薄板與聲腔耦合系統

薄板結構與聲腔耦合系統是工業上廣泛應用的系統結構，如汽車車身與內部聲腔。而添加阻尼也成為噪聲控制的重要和基本的手段。在驗證了以波函數法實現含有自由阻尼的薄板彎曲振動的基礎上，進一步對此類結構的聲固耦合系統的響應進行分析驗證。該耦合系統的幾何及尺寸如圖7所示，在板上取一點(0.2 m，0.2 m，0.5 m)施加單元力，取R點(0.4 m，0.3 m，0.2 m)處的聲壓響應。

該基于波函數法的耦合模型也在Matlab中建立和完成后處理。有限元耦合模型則在LMS.Virtual.lab中建立和計算，其中精細的有限元模型除了結構與阻尼的單元外增加了3 000 000個聲學六面體單元，而普通單元尺寸模型則增加了120 000個聲學六面體單元。為了驗證阻尼的作用，同樣也對無阻尼耦合模型進行了計算。得到的頻響曲線如圖8、圖9所示。與薄板振動響應的結果一致，基于波函數法的計算結果與精細的有限元模型更接近，而普通單元尺寸的有限元模型在較高頻率段的偏移明顯。添加阻尼后的模型在很多波峰處的響應得到了很大抑制，整體的聲壓級水平也較無阻尼系統要小。

圖7 薄板聲腔耦合系統Fig.7 Geometry of coupled vibro-acoutic system

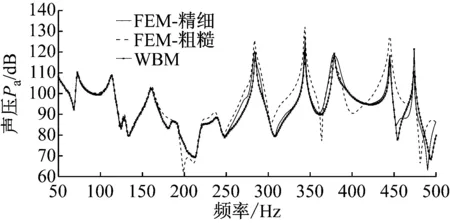
圖8 含阻尼耦合系統聲學響應Fig.8 Acoustic response of reference point with damp

圖9 不含阻尼耦合系統聲學響應Fig.9 Acoustic response of reference point without damp

4.3收斂性

通過以上的算例可以看出波函數法在計算含有自由阻尼的薄板聲腔等系統的聲振響應的正確性，然而該方法能更好的處理中頻問題則主要是其擁有高計算精度與效率。為描述計算方法的收斂性，定義相對誤差ε

(23)

式中:R(p)為選取點的振動或聲學響應;Rref(p)為參考響應值，此處取精細建模的有限元計算結果。

圖10、圖11分別為自由阻尼薄板算例與結構聲耦合算例在相同硬件條件下，在100 Hz時關于計算時間的收斂曲線。雖然波函數法的計算時間包括建模與計算的時間，而有限元法的物理計算時間只包括模型計算時間(前期有限元模型劃分與生成的時間未包含)，但對于該類較簡單的結構波函數法模型的構建時間很短，對對比結果影響較小。從收斂曲線可以看出，在相同計算精度的情況，波函數法的計算效率高于有限元法。而對于更高頻段的聲振響應問題，就要求單元尺寸要足夠小來捕捉短波特性。這就使得模型計算量變得十分巨大，而伴隨的還有邊界離散帶來的誤差累積，所以基于單元的方法主要用于求解低頻問題。波函數法沒有如單元類方法采用多項式擬合造成的差值誤差，同時相比之下其計算量也非常小，因此其能更好的應用于中頻問題以及需要重復計算類問題如優化迭代。

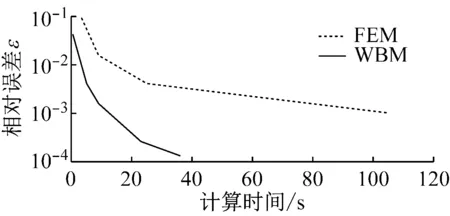
圖10 薄板結構中WBM與FEM的收斂曲線Fig.10 The convergence of WBM and FEM of the plate model

圖11 耦合系統中WBM與FEM的收斂曲線Fig.11 The convergence of WBM and FEM of the coupled system

5 結 論

文章在完成敷設自由阻尼薄板的彎曲振動響應的分析基礎上，應用波函數法理論，推導了自由阻尼薄板結構以及其與聲腔耦合的WBM模型，實現了波函數法對含有自由阻尼結構的聲振預測。以兩個數值模型驗證該方法的正確性，得到了自由阻尼在中頻對薄板類結構的減振作用與效果。通過與有限元法在頻響結果與收斂性的對比，體現了波函數法更能有效的處理含有自由阻尼結構系統在更高頻段的聲振響應問題，也說明了此次探究的有效性。后續將在此基礎上，探尋基于Middlin理論下，含有阻尼的板件類弱結構在中頻的響應預測方法，以及基于結構或聲學響應的阻尼優化。

[1] DERAEMAEKER A, BABUSKA I, BOUILLARD P. Dispersion and pollution of the FEM solution for the helmholtz equation in one, two and three dimensions [J]. International Journal for Numerical Methods in Engineering, 1999,46(4):471-499.

[2] ZIENKIEWICZ O C, TAYLOR R L, ZHU J Z, et al. The finite element method-Vol. 1: Basic formulation and linear problems[M]. Oxford: Butterworth-Heinemann, 2005.

[3] LYON R, DEJONG R. Theory and application of statistical energy analysis [M]. 2nd ed. Oxford: Butterworth Heinemann, 1995.

[4] MENCIK J M, ICHCHOU M N. Wave finite elements in guided elastodynamics with internal fluid[J]. International Journal of Solids and Structures, 2007,44:2148-2167.

[5] MAXIT L, GUYADER J L. Extension of SEA model to subsystems with non-uniform modal energy distribution[J]. Journal of Sound and Vibration, 2003,265(2):337-358.

[6] SESTIERI A, CARCATERRA A. On the spurious solutions in complex envelope displacement analysis[J]. Journal of Sound and Vibration, 2001,240(2):293-302.

[7] LADEVEZE P, ARNAUD L, ROUCH P, et al. The variational theory of complex rays for the calculation of medium- frequency vibrations[J]. Engineering Computations, 2001, 18(1/2):193-214.

[8] LANGLEY R S, CORDIOLI J A. Hybrid deterministic-statistical analysis of vibroacoustic system domain couplings on statistical components[J]. Journal of Sound and Vibration, 2009, 321(3/4/5):893-912.

[9] MACE B R. Statistical energy analysis, energy distribution models and system modes[J]. Journal of Sound and Vibration, 2003, 264(2):391-409.

[10] DESMET W. A wave based prediction technique for coupled vibro-acoustic analysis[D]. Leuven：Katholieke Universiteit Leuven，1998.

[11] VANMAELE C, VANDEPITTE D. An efficient wave based prediction technique for plate bending vibrations[J]. Computer Methods in Applied Mechanics and Engineering, 2007,196(33/34): 3178-3189.

[12] VAN GENECHTEN B, ATAK O, BERGEN B, et al. An efficient wave based method for solving helmholtz problems in three-dimensional bounded domains[J]. Engineering Analysis with Boundary Elements, 2012,36(1):63-75.

[13] DESMET W, VAN HAL B, SAS P, et al. A computationally efficient prediction technique for the steady-state dynamic analysis of coupled vibro-acoustic systems[J]. Advances in Engineering Software, 2002,33(7/8/9/10):527-540.

[14] DECKERS E, HORLIN D E, VANDEPITTE D, et al. A wave based method for the efficient solution of the 2d poroelastic biot equations[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 201/202/203/204:245-262.

[15] 何雪松,黃其柏,胡溧.WBM 法在薄板彎曲振動分析中的應用[J].華中科技大學學報(自然科學版),2008,36(7):97-99.

HE Xuesong, HUANG Qibai, HU Li. Application of wave based method to plate bending vibration analysis [J]. Journal of Huazhong University of Science and Technology (Natural Science), 2008, 36(7):97-99.

[16] PENG Weicai, HE Zeng, LI Peng, et al. A prediction technique for dynamic analysis of flat plates in the Mid-Frequency Range[J]. Acta Mechanica Solida Sinica, 2007, 20(4): 333-341.

[17] 何锃, 彭偉才,王加強. WB法分析結構與聲耦合問題[J]. 華中科技大學學報(自然科學版), 2007,35(8): 119-121.

HE Zeng,PENG Weicai, WANG Jiaqiang. Wave based method for coupled structural—acoustic analysis[J]. Journal of Huazhong University of Science & Technology (Natural Science),2007,35(8): 119-121.

[18] 桂洪斌，趙德有，金咸定. 自由阻尼層加筋板的穩態簡諧響應分析[J]. 上海交通大學學報,2002,36(11):1544-1547.

GUI Hongbin, ZHAO Deyou, JIN Xianding. Steady-state harmonic response analys is of stiffened plate with unconstrained damped layer[J]. Journal of Shanghai Jiaotong University, 2002,36(11):1544-1547.

[19] REDDY C V R，GANESAN N，RAO B V A，et al. Response of plates with unconstrained layer damping treatment to random acoustic excitation[J]. Journal of Sound and Vibration,1980,69(1): 35-43.

Responsesofunconstraineddampedvibro-acousticsystemsusingthewavebasedpredictiontechnique

XIA Xiaojun1,2, XU Zhongming1,2, LAI Shiyang3, ZHANG Zhifei1,2, HE Yansong1,2

(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China;2. School of Automotive Engineering, Chongqing University, Chongqing 400030, China;3. School of Mechanical Engineering, Chongqing Vocational Institute of Engineering, Chongqing 402260, China)

The global governing vibration equation of an unconstrained damped plate was deduced based on the Kirchhoff theory and the analysis of the complex stiffness. The methodology for predicting the vibration of the unconstrained damped plate and the acoustics of the coupled 3D vibro-acoustic system was proposed by virtue of the wave based method (WBM). Taking a four edges clamped rectangular plate coupled with a box like vibro-acoustic system as a numerical example, the out-plane displacement of the unconstrained damped plate was analysed. The responses at a selected reference point was calculated in the 50-500 Hz frequency band by using the WBM and FEM respectively. The results of the two method validate that the WBM is capable for predicting the vibration and acoustic responses of the unconstrained damped system effectively, and the WBM is more efficient to deal with vibro-acoustic problems compared with the FEM.

unconstrained damping; wave based method; bending vibration; structural-acoustic coupling

U467.4

A

10.13465/j.cnki.jvs.2017.19.024

重慶市基礎與前沿研究計劃項目(CSTC2015JCYJBX0075);中央高校基本科研業務費(106112016CDJZR335522)

2016-05-04 修改稿收到日期：2016-08-10

夏小均 男，博士生，1988年生

徐中明 男，博士，教授，博士生導師，1963年生