永磁力矩電機三相繞組不對稱性改進方法研究*

葛紅巖, 卓 亮, 劉 勇, 楊榮江,2

(1. 貴州航天林泉電機有限公司,貴州 貴陽 550008；2. 國家精密微特電機工程技術研究中心,貴州 貴陽 550008)

永磁力矩電機三相繞組不對稱性改進方法研究*

葛紅巖1, 卓 亮1, 劉 勇1, 楊榮江1,2

(1. 貴州航天林泉電機有限公司,貴州 貴陽 550008；2. 國家精密微特電機工程技術研究中心,貴州 貴陽 550008)

由于力矩電機多作為驅動電機使用，且電機對低速平穩性要求很高，所以選用了一種特殊的極槽配合方式。12極39槽的選擇使得電機齒槽轉矩較小的同時導致電機三相繞組不對稱。降低繞組不對稱對電機低速平穩性的影響，對提高繞組的對稱性的方法研究有著重要的意義。以一臺采用12極39槽的力矩電機為例，提出了一種繞組不對稱性的改進方法，通過改變繞組的排列方式提高了繞組的對稱性，且保證了電機的低速平穩性。最終通過理論研究與仿真分析驗證了不對稱性改進方法的有效性。

力矩電機；低速平穩性；不對稱；改進方法

0 引 言

永磁力矩電機根據有無電刷可分為有刷力矩電機和無刷力矩電機。無刷力矩電機根據驅動方式分為正弦波驅動電機和方波驅動電機。正弦波驅動電機是通過信號電機反饋位置信號，電機的轉速平穩性能直接影響電機的控制精度，特別對于永磁力矩電機來說，電機轉速較低，易受到齒槽轉矩的影響；同時，力矩電機為了保證電機力矩輸出能力，而不采用斜槽或斜極來降低電機的齒槽轉矩[1-6]，故國內外力矩電機大多通過極槽配合的選取作為降低齒槽轉矩的主要方法，其他的方法如開輔助槽、優化極弧系數等都是以極槽配合的選擇為基礎，故極槽配合的選擇是力矩電機的設計要點之一[7-13]。在多種極槽配合的選擇下，會有很多種情況三相繞組不對稱，會對轉矩產生較大的波動，故對不對稱繞組對稱性能改進方法的研究有著重要的意義[14-20]。

本文以一臺正弦波驅動的永磁力矩電機為例，選擇了12極39槽的極槽配合來降低齒槽轉矩。為了改進該極槽配合導致的三相繞組不對稱性，通過改變繞組排布的方法增加了三相繞組的對稱性，通過理論研究與仿真分析，驗證了該方法的有效性。

1 極槽配合的選擇對齒槽轉矩影響

力矩電機極槽配合的選擇，主要目的是為了減小齒槽轉矩。在抑制齒槽轉矩時，首先考慮槽數Z和極數2p組合與齒槽轉矩的關系。通常認為，基波齒槽轉矩周期數γ越大，其幅值就越小。所以宜選擇最小公倍數2p較大的定子槽數Z和轉子極數2p組合。

本文力矩電機采用分數槽繞組。采用分數槽繞組電機有利于降低齒槽轉矩的原理在于：各個槽口所處磁場位置不同，所以各自產生的齒槽轉矩相位便不同，從而疊加的結果不但提高了基波齒槽轉矩周期數，并有可能產生相互抵償的作用。整數槽繞組電機每個磁極下的齒槽個數和位置都是相同的，在所有極下產生的齒槽轉矩相位相同，2p個極的齒槽轉矩疊加起來使總齒槽轉矩大為增加。

在定轉子相對位置變化一個齒距范圍內，齒槽轉矩是周期性變化的，變化的周期數取決于極數和槽數的組合。一個齒距范圍內齒槽轉矩的周期數NP為極數、槽數與極數最大公約數的比值，即

從文獻[15]的結論可以得出，Np越大則齒槽轉矩越小，故選擇合適的極槽配合能夠有效地降低齒槽轉距。下面分析極數為12極，槽數選擇能夠保證三相繞組對稱的幾種典型極槽配合，如表1所示。

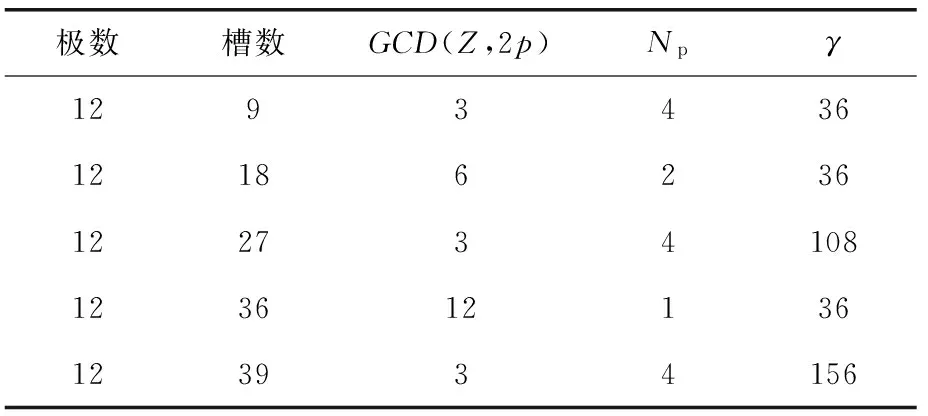
表1 極槽配合明細表

從表1中可知，在電機尺寸一定范圍內，對于12極力矩電機來說，應選擇周期數較大的，以降低齒槽轉矩，12極39槽一個槽內齒槽轉矩周期數Np為4，為所列表中最大值之一，且基波齒槽轉矩周期數γ最大，整個電機在某些定子尺寸范圍內，12極39槽為力矩電機最適合的極槽配合。

2 雙層繞組不對稱性分析

對12極39槽電機的繞組排列進行研究，可知電機的每極每相槽數為分數，即

由式(2)可知d=12，故從文獻[2]中的結論可以得出，該極槽配合使得三相繞組不對稱。本根據傳統方法“湊整”法可以將電機的槽數分成三個單元，每個單元的循環數序相同，而本文采用了新的繞組排序方法，如表2所示。

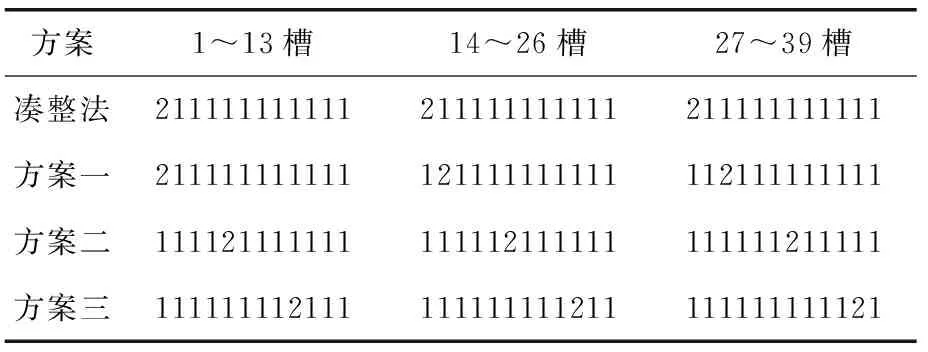
表2 循環數序表

根據表2的循環數序得到繞組的排列分布，如表3所示，其中四種排列方式都為雙層繞組，繞組排列循環數序和分布都指為雙層繞組的上層繞組。

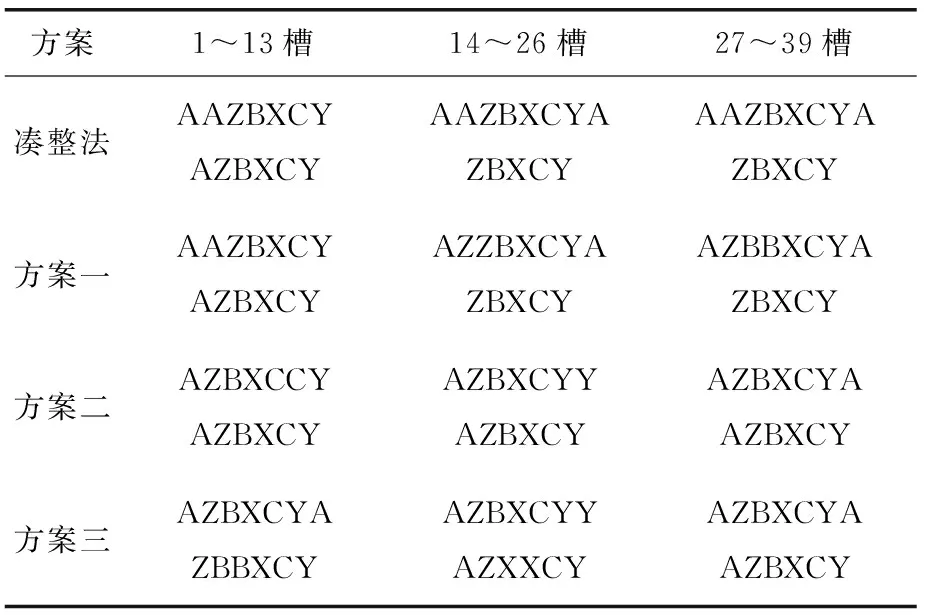
表3 繞組排列表

從表3可以明顯看出，每相槽數不相等，三相繞組的對稱性一定很差，故對稱性的改進方法首先要滿足每相槽數相等，且主波合成槽矢量盡可能接近對稱。如表2所示，本文采用的方案一，通過改變循環數序中“2”的位置，保證了每相槽數相等。通過方案一的延伸得到方案二和方案三，將空間中每槽的位置以復數形式表示，以相量法為計算方法通過編程計算得到4種方法的相間夾角及每相繞組的主波分布系數，如表4和表5所示。

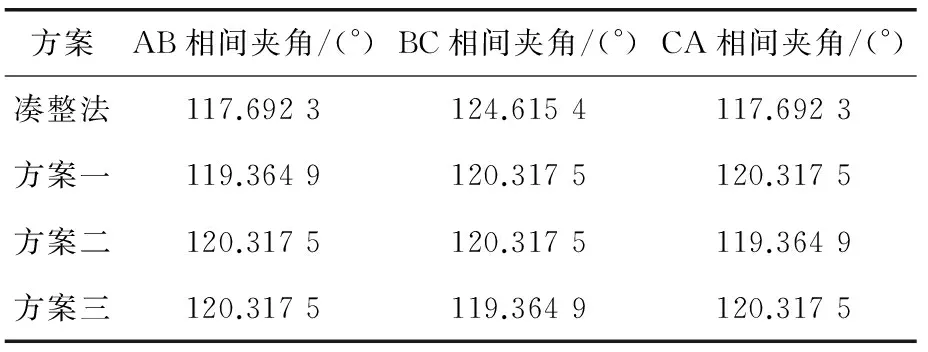
表4 雙層繞組相間夾角分布表

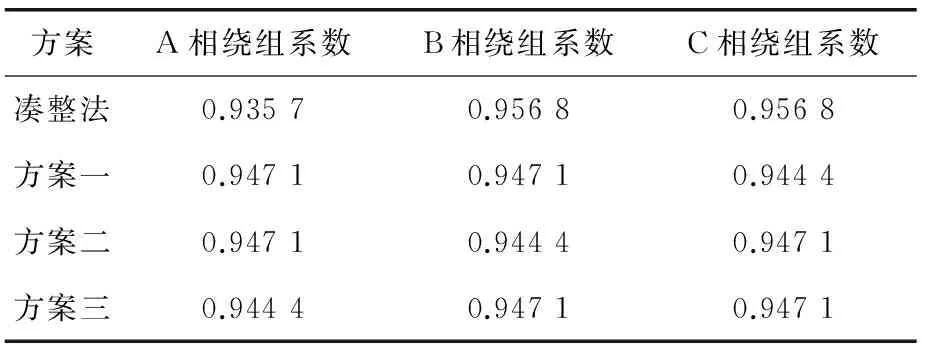
表5 雙層繞組每相主波分布系數表

從表4和表5可以看出，“湊整”法排列的繞組從相間夾角和分布系數角度來看，主波合成矢量的對稱性是很差的，方案一、二、三的繞組對稱性較“湊整”法好很多，同時，如果將ABC三相不做特別區分，方案一、二、三的繞組對稱性從電機整體性能角度來說是相同的。

3 多層繞組組合不對稱性分析

雖然方案一、二、三對繞組的對稱性有了很大的改進，但對于力矩電機來說，有時對電機的低速平穩性能有著很高的要求，方案一、二、三可能不能滿足使用要求。故為了進一步改進繞組對稱性，本文將方案一、二、三兩兩組合或者三者合一，得到四層或者六層繞組，通過計算得到4種組合的相間夾角及每相繞組的主波分布系數，如表6和表7所示。

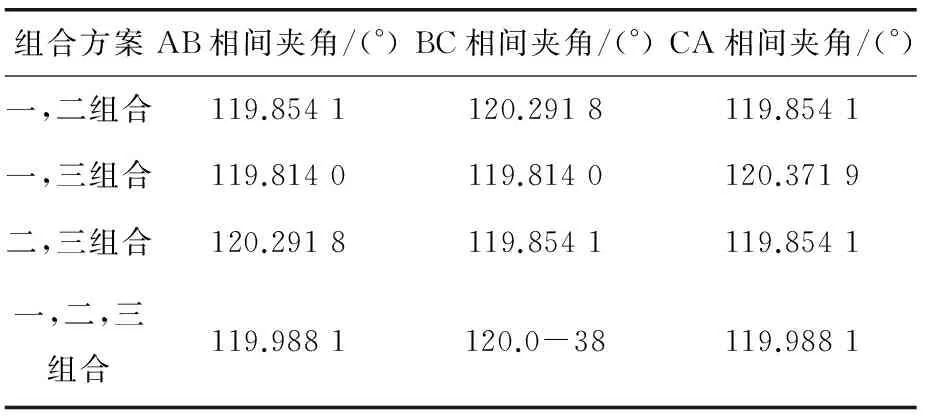
表6 多層繞組相間夾角分布表

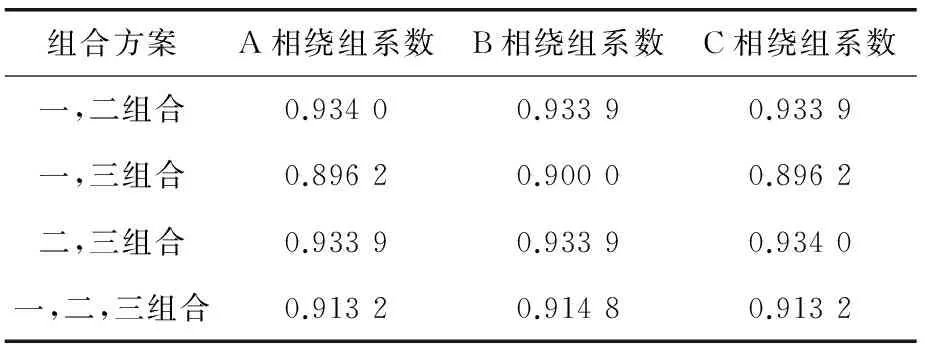
表7 多層繞組每相主波分布系數表

從表6和表7可以看出，4種方案中，方案一、二、三“三合一”的組合從相間夾角的角度看對稱性最好，方案一、二組合和方案二、三組合從分布系數的角度看對稱性最好，且從兩個角度看對稱性都優于單獨的方案，方案一、三組合從兩個角度看對稱性都是最壞的。如果將ABC三相不做特別區分，方案一、二組合和方案二、三組合的繞組對稱性從電機整體性能角度來說是相同的。如果不看方案一、三組合，從雙層變為多層，分布系數隨著層數的增多而變小，這對電機的性能有一定的影響，要分析這種影響以及從兩個角度來綜合對比“三合一”方案和“兩兩組合”方案的對稱性，本文從仿真的結果來提供數據參考。

4 仿真結果與試驗對比分析

本文以一臺12極39槽且繞組為“三合一”方案的樣機為參考，通過試驗測量與仿真結果對比，驗證仿真結果的正確性，從而為通過仿真分析繞組排列對電機性能影響提供依據。圖1為電機有限元仿真模型，圖2為樣機的定子和轉子，圖3為樣機負載測試試驗臺。

圖1 電機有限元模型

圖2 分裝式電機定、轉子

圖3 電機負載測試試驗臺

通過仿真計算與試驗測量得到仿真數據與試驗數據，將實測和仿真數據的幾個工作點進行對比分析，如圖4所示；得到仿真結果的誤差數據，如圖5所示。

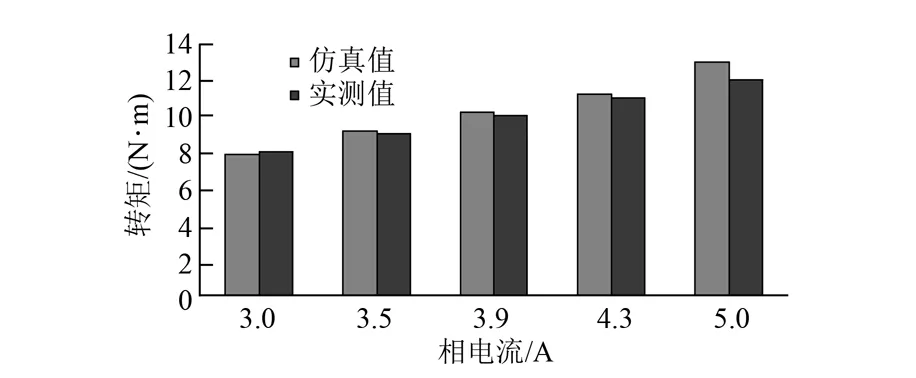
圖4 仿真結果與試驗數據對比圖

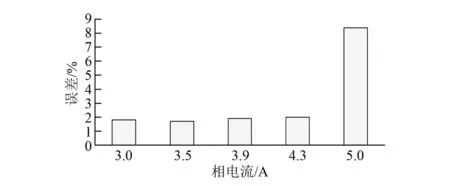
圖5 仿真結果誤差分布圖

從圖5數據分析可以看出，相電流5 A工作點的誤差較大。從圖4可以看出該工作點實測值較仿真值小，分析是由于樣機電流過大，繞組磁勢較大，電機氣隙磁場飽和程度較高，使電機的轉矩系數降低。有限元法計算磁場飽和點時計算準確性較低，但從圖5前幾個工作點可以看出，在氣隙磁場不飽和的情況下，仿真誤差可達到5%以下，能夠保證仿真準確性。因此，可以通過仿真分析繞組排列對氣隙磁場不飽和電機性能的影響。

5 繞組排列仿真分析

通過仿真分析繞組排列對電機性能的影響，以2層繞組表示方案一、二、三中任意一個，以4層繞組表示方案一、二或者方案二、三的組合，以6層繞組表示方案一、二、三“三合一”組合，從轉矩系數和轉矩波動系數兩個方面分析2、4、6層繞組的電機性能，通過仿真得到不同方案的仿真結果，如圖6和圖7所示。

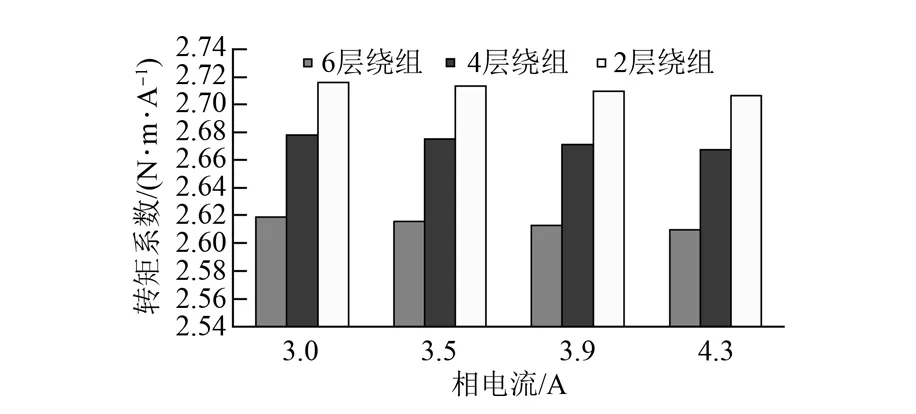
圖6 仿真結果誤差分布圖

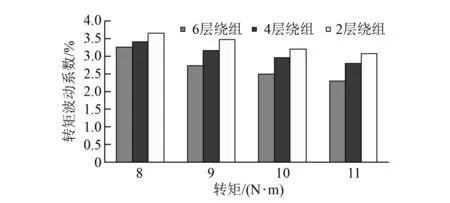
圖7 仿真結果誤差分布圖

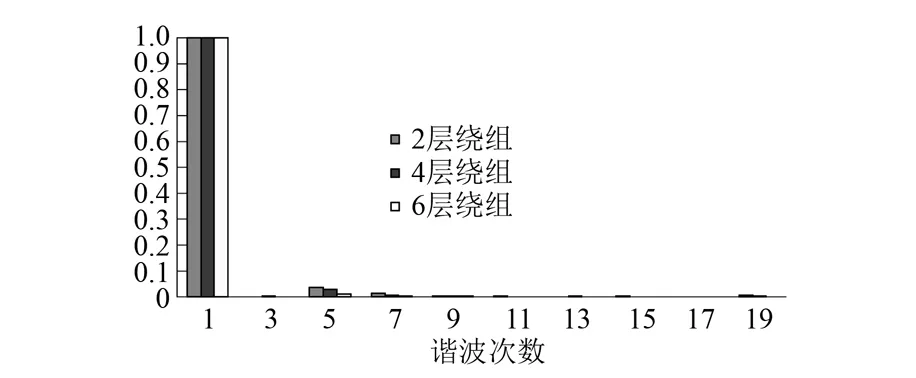
圖8 AB線磁動勢諧波分布圖

從圖6可以看出，隨著繞組層數的增多，轉矩系數隨之變小，相同相電流下，輸出的轉矩變小，電機的力矩輸出能力有所降低。從圖7可以看出，隨著繞組層數的增多，轉矩波動系數隨之變小，相同輸出轉矩下，電機的轉矩波動小，電機的低速平穩性能提高。從繞組磁動勢的角度來分析不同繞組排列對轉矩波動的影響，由于不同繞組排列主波系數不等，這里將主波系數都調整成1，其他次諧波隨著變化，同時由于三相繞組不對稱，故比較2、4、6層繞組的AB、BC、CA的線磁動勢各次諧波大小，通過編程計算得到結果，如圖8～圖10所示。

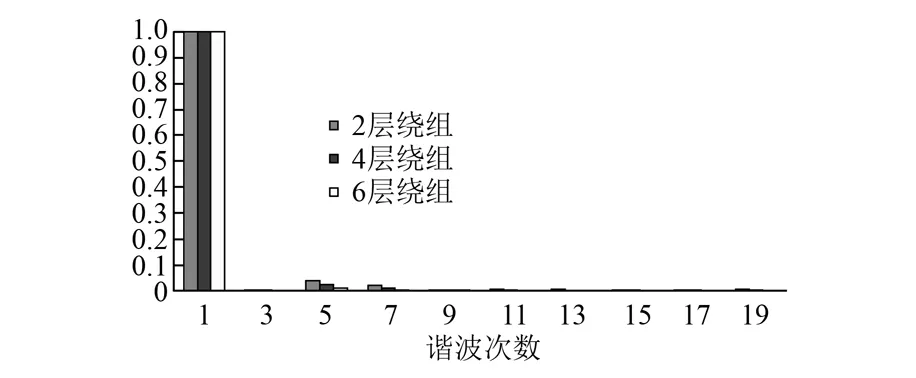
圖9 BC線磁動勢諧波分布圖

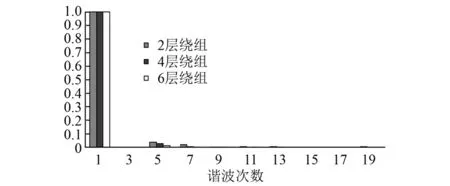
圖10 CA線磁動勢諧波分布圖

從圖8～圖10可以看出，由于三相繞組的對稱性得到了很大的改善，三相間的各線磁動勢的各次諧波分布基本相同，都是5次和7次諧波所占比重較大。可見，這是影響轉矩波動的主要諧波次數，隨著繞組層數的增多，5次和7次諧波的幅值明顯降低，故轉矩波動也隨之降低。

6 結 語

本文通過理論分析得到12極39槽的極槽配合能夠有效地降低齒槽轉矩，通過繞組排列的重新排布得到了一種三相對稱性較好的排布方式，通過編程計算相間夾角及主波系數可以證明此繞組排布對三相對稱性進行了有效的改進。通過仿真與試驗數據對比，證明了仿真結果的有效性，對比3種改進方案的仿真結果，可以看出，3種方案中轉矩系數大的則轉矩波動也較大，故選擇電機設計方案時，可根據實際技術要求選擇合適的方案。

[1] 夏加寬,劉力夫.取向硅鋼片近極槽數永磁同步力矩電機轉矩分析[J].微特電機,2015,43(2): 23-26.

[2] 孫昌志.釹鐵硼永磁電機[M].沈陽:遼寧科技出版社,1997.

[3] 唐任遠.現代永磁電機[M].北京:機械工業出版社,1997.

[4] 湯蘊璆.電機內的電磁場[M].北京:科學出版社,1998.

[5] 夏加寬,盛麗君,劉純江.直接驅動環形永磁力矩電機低速齒槽轉矩脈動補償研究[J].電氣技術,2009(3): 21-24.

[6] 尹翔陵,王愛祥.直流力矩電機在精密跟蹤雷達中的應用[J].電子工程師,2001,27(1): 55-57.

[7] 姚紅萍.基于無刷直流力矩電機的雷達搜索系統工程設計[J].微電機,2012,45(12): 70-74.

[8] 楊玉波,王秀和,丁婷婷,等.極弧系數組合優化的永磁電機齒槽轉矩削弱方法[J].中國電機工程學報,2007,27(6): 7-11.

[9] 陳永校,湯宗武.小功率電動機[M].北京:機械工業出版社,1992.

[10] 羅宏浩,廖自力.永磁電機齒槽轉矩的諧波分析與最小化設計[J].電機與控制學報,2010,14(4): 36-40.

[11] 王宗陪.永磁直流微電機[M].南京:東南大學出版社,1992.

[12] 李鐘明,劉衛國.稀土永磁電機[M].北京:國防工業出版社,1999.

[13] 王秀和.永磁電機[M].北京:中國電力出版社,2012.

[14] 李明陽,姚慶雙.定子為不對稱繞組的排列及諧波分析[J].防爆電機,2011,46(2): 14-17.

[15] 李林合,梁艷萍,黃浩.水輪發電機定子繞組不對稱支路電磁參數計算模型[J].電機與控制學報,2006,10(5): 283-286.

[16] 王東,馬偉明,顧偉峰,等.12/3相雙繞組感應發電機的諧波不對稱分析[J].中國電機工程學報,2004,24(5): 148-152.

[17] 楊孝謙.三相不對稱繞組的引用[J].防爆電機,2006,41(4): 15-16.

[18] 潘曉晟,趙宏亮,王曉文.一種分析兩相不對稱繞組電機的新方法[J].微特電機,2000,28(3): 24-26.

[19] 戈寶軍,李明哲,孫玉田,等.同步發電機不對稱運行工況阻尼繞組電流的計算[J].中國電機工程學報,2013,33(27): 154-160.

[20] 李林合,梁艷萍.汽輪發電機支路不對稱定子繞組連接問題的探討[J].防爆電機,2006,41(3): 1-4.

AsymmetryImprovedMethodforPermanentMagnetTorqueMotorThree-PhaseWindings*

GEHongyan1,ZHUOLiang1,LIUYong1,YANGRongjiang1,2

(1. Guizhou Aerospace Linquan Motor Co., Ltd., Guiyang 550008, China;2. National Precision Micro Motor Engineering Research Center, Guiyang 550008, China)

Since most torque motors were used as the drive motors, and low speed stability was highly required, a special way of poles with slots was chosen. Selected the 12 pole 39 slots made the motor cogging torque small, but motor three-phase windings were asymmetry. There was important significance of research on the method of improving the symmetry of the winding to reduce the impact asymmetry of motor windings to the low speed stability. In a 12 pole 39 slot motor torque case, a method to improve the winding asymmetry was proposed, and the winding arrangement were changed to improve the symmetry of the windings, and the low speed stability of motor could be guaranteed. Finally, the validity of the method were verified by theoretical research and simulation analysis.

torquemotor;lowspeedstability;asymmetric;improvedmethod

大力矩、低脈動交流永磁力矩電機及其驅動與控制系統(JPPT-125-GH-154)

葛紅巖(1989—)，男，助理工程師，研究方向為永磁電機設計與多物理場計算。

TM 359.6

A

1673-6540(2017)10- 0083- 05

2016 -11 -09