出口海陸倉融資質押率優化
王滋承,周 詠,楊華龍,2
(1.大連海事大學交通運輸管理學院,遼寧 大連 116026;2.大連海事大學綜合交通運輸協同創新中心,遼寧 大連 116026)
出口海陸倉融資質押率優化
王滋承1,周 詠1,楊華龍1,2
(1.大連海事大學交通運輸管理學院,遼寧 大連 116026;2.大連海事大學綜合交通運輸協同創新中心,遼寧 大連 116026)
出口海陸倉融資對促進海運貿易和供應鏈金融發展具有重要的現實意義,其質押率優化是融資風險管理和控制決策的關鍵。本文針對需求波動條件下的出口海陸倉融資質押率優化問題,應用雙重Stackelberg博弈原理,分析構造了船公司、出口商、進口商之間四種博弈策略下的總利潤函數,以供應鏈總利潤最大化為目標,構建了質押率分段函數優化模型,在論證了質押率最優解存在的基礎上,采用反向推理法設計了求解步驟。算例驗證了模型的適用性和有效性,結果表明,船公司最優質押率與出口商最佳交貨提前期、進口商最優訂貨批量均呈負相關關系,質押貨物市場售價越高,最優質押率越低。在進口商質押貨物進貨價上升或出口商原材料購買價格下降時,提高存貨融資質押率,有助于提高海運貿易供應鏈的整體利益。
出口海陸倉;融資;質押率;雙重Stackelberg博弈;反向推理法
1 引言
海陸倉融資是指船公司基于倉單質押理念,將其在陸上倉庫的貨物質押與海上在途的貨物質押相連接,為進/出口商提供的一種貨物質押融資模式,以實現海運貿易供應鏈中物流、信息流和資金流的同步化。海陸倉融資在緩解進/出口商資金不足的同時,也為銀行、船公司提供了新的利潤增長點,對促進海運貿易和供應鏈金融發展具有重要的現實意義,已得到社會各界充分重視。
海陸倉融資分為進口海陸倉融資與出口海陸倉融資兩種類型,進口海陸倉融資是指船公司將海上在途的貨物質押與目的地倉庫的貨物質押相連接,為進口商提供的一種貨物質押融資模式;出口海陸倉融資是指船公司將其在發貨地倉庫的貨物質押、海上在途的貨物質押以及目的地倉庫的貨物質押連接起來,為出口商提供的一種全程貨物質押融資新模式。前者包含“海-陸”質押流程,后者則包含“陸-海-陸”質押流程。
在海陸倉融資業務中,一個重要的理論和實踐問題是船公司如何確定質押率,即貸款本金與質押貨物價值的比率。國內外學者對質押率確定問題展開了許多有益的研究。Frye等[1]將質押貨物價值的波動性量化,并建立了基于違約風險的質押率債券模型;Cossin等[2]結合信用和利率風險計算了貸款企業違約概率外生情況下的質物貸款折扣率;Buzacott和Zhang[3]分析了存貨融資中企業的生產決策及銀行的利率與貸款限額決策,令銀行通過調整利率與貸款額控制企業的庫存決策與質押貨物的變現風險;Damjanovic和Girdenas[4]證明了貨幣乘數和房價、質押率呈正相關關系;于輝和甄學平[5]用Stackelberg博弈和VaR風險計量研究了銀行追求利潤最大化和權衡風險收益兩種情形下的質押率;易雪輝和周宗放[6]以期望利潤最大化為目標建立雙重Stackelberg博弈模型,通過逆向歸納法得出決策;李毅學等[7-8]研究了重隨機泊松違約概率下銀行的風險控制指標-質押率決策,并用Stackelberg博弈分析了在季節性存貨融資下,借款企業和物流企業的再訂購決策和質押率決策;張興國和劉鵬[9]考慮價格波動、企業減排、違約和宏觀經濟等風險,構建了CERs收益權質押融資業務的質押率模型;匡海波等[10-11]建立了低碳港口物流約束條件下質押貸款組合優化決策模型,界定單筆港口貨類質押貸款的VaR質押率。在海陸倉融資問題方面,嚴飛和汪傳旭[12-13]建立了根據進口商最佳進貨量及質押量的船公司質押率優化模型、貨物價格呈布朗運動規律的海陸倉融資收支利率優化模型,用Stackelberg博弈分析船公司和進口商的收益;潘意志等[14]對海陸倉質押融資貸款的業務模式、特點、優勢及風險控制進行了分析;王功榮等[15]結合航運實踐,介紹了航運企業在海陸倉融資方式中的法律風險與防范途徑;廖鑫凱等[16]提出“出口海陸倉”概念,對其運作方式、風險控制和優勢進行了解釋。
綜上,質押率的確定過去幾年一直是國內外研究的熱點問題。海陸倉融資質押率問題的研究主要側重于進口商海陸倉融資,對出口海陸倉融資問題研究主要以定性分析為主,且在質押流程方面,現有研究也將出口海陸倉融資和進口海陸倉融資相混淆。為此,本文針對出口海陸倉融資與進口海陸倉融資在流程和質押率方面的區別,對需求波動情況下出口海陸倉融資的質押率進行優化,以期使船公司、出口商、進口商供應鏈總利潤最大化。
2 問題描述
在海運貿易中,通常涉及出口商、進口商、銀行和船公司四方。出口海陸倉融資是一種統一授信存貨質押融資模式,出口商為了盡快獲得資金以保障生產經營的順利進行,將已生產的貨物質押給銀行,銀行委托船公司對貨物全程質押運輸和監管。船公司通過制定一個合理的質押率,為在其海陸倉內的該批質押貨物確定融資額度,銀行以船公司的信用作為擔保條件,根據船公司確定的融資額度向出口商提供該額度的貸款,船公司則對出口商該筆貸款的使用情況進行監管,并以該批貨物作為質押品確保其信用擔保的安全,以形成封閉式與自償性的一般要求。出口海陸倉融資流程如圖1所示:

圖1 出口海陸倉融資流程
由圖1可見,船公司受銀行委托,負責運輸和監管質押貨物,評估質押貨物市值并設定合理質押率,從而確定為質押貨物進行擔保貸款的額度,銀行據此向出口商發放該額度的貸款。若出口商違約,船公司則可通過變賣質押貨物向銀行補足資金敞口,使得銀行基本不承擔該融資項目的風險。
由此可見,在出口海陸倉融資業務中,實際參與交易決策的主體是船公司、出口商和進口商三方,交易決策體現為雙重Stackelberg博弈的關系。第一重博弈發生在船公司和出口商之間,船公司首先設定質押率,出口商據此從銀行獲得相應額度的貸款,利用該項貸款繼續生產,并根據所生產出的貨物數量確定出交貨提前期。在第一重博弈中,船公司為博弈的主導者,出口商為服從者。第二重博弈發生在出口商和進口商之間,出口商確定交貨提前期,進口商據此確定訂貨批量。出口商為博弈的主導者,進口商為服從者。
在出口海陸倉融資業務中,質押貨物市場需求隨機波動會導致質押貨物市場售價發生變動。當質押貨物市場售價大于進口商與出口商簽訂的購貨價格時,進口商會正常提貨;當質押貨物市場售價不大于購貨價格時,進口商就有可能違約不提貨,進而使得出口商也有可能違約不還款,船公司則可能需要變賣貨物以彌補損失。因此,出口海陸倉融資違約的基礎在于質押貨物市場需求波動導致的市場售價變化。在需求波動的情況下,進口商、出口商、船公司三方之間會出現以下幾種的履約情形,如圖2所示。

圖2 進口商、出口商、船公司履約情況
由圖2可見,當需求波動時,進口商、出口商、船公司三方之間對應有4種可能的雙重Stackelberg博弈策略:策略1{不違約,不違約,不變賣貨物}、策略2{違約,不違約,不變賣貨物}、策略3{違約,不違約,變賣貨物}、策略4{違約、違約、變賣貨物}。質押貨物市場需求的不確定性包括需求上升、不變和下降。顯然,當市場需求波動,但進口商對質押貨物的售價仍高于其進貨價時,進口商、出口商、船公司三方會選擇博弈策略1。當進口商對質押貨物的售價不高于其進貨價時,進口商可能違約不再提取貨物,出口商可能隨之不再還貸,船公司則會變賣貨物以補足擔保所產生的資金敞口,于是,進口商、出口商、船公司三方則可能會選擇上述任何一種博弈策略。由此可知,在三方的雙重Stackelberg博弈關系中,船公司設定的質押率不僅影響出口商的交貨提前期,并進一步影響進口商的訂貨批量,而且還會影響進口商、出口商、船公司三方的博弈策略,從而對船公司、出口商、進口商三方的整體供應鏈利潤產生影響。因此,出口海陸倉融資質押率優化,就是通過確定需求波動情況下的最優質押率,以使海運貿易供應鏈總利潤最大。
3 質押率優化決策
3.1參數和變量設定
根據前述問題描述,本文做以下假設:(1)出口商為生產型企業,進口商為銷售型企業,雙方簽訂長期的買賣合同;(2)允許缺貨,貸款期間內出口商貨物存于船公司倉庫;(3)貸款期間,船公司根據貸款額度收取利息(融資服務費);(4)若進口商選擇提貨,則出口商一定要補貨還貸以解押提單,令船公司放貨;(5)進出口貿易條件為FOB,將海運運費及保險費計入進口商成本;(6)貨物需求隨機波動,處理價不低于其原材料價格,不高于進貨價。
為便于出口海陸倉融資質押率優化問題的建模與求解,本文引入以下參數:m為融資服務費率;Ce為出口商生產準備成本,Ci為進口商訂貨固定成本;he和hi分別為出口商和進口商每單位貨物的倉儲費用,hs為船公司倉庫管理費用;pe和pi分別為進口商單位商品進貨價和售價;pa和pb分別為單位商品原材料價格和處理價;P為出口商生產率;k為進口商庫存消耗速度;s為進口商安全庫存;缺貨時,進口商會給等待的顧客一定的價格折扣α;ε為缺貨時愿意等待的顧客比例;ω和?分別為船公司的單位運價和海運成本;λ為保險費率;ξ為保險加成率;q為質押余量;L為出口商交貨提前期,即進口商發出訂貨通知到貨物進入船公司境外監管倉所持續的時間長度;Q為進口商訂貨批量;r為船公司給出的質押率,rm為質押率下限,rw為質押率上限;v和μ分別表示進口商缺貨量和平均庫存水平;T為海運時長;ti為進口商庫存從到貨到售罄的時長;te為出口商發貨周期時長。
3.2不同策略下的利潤函數
假設船公司給定了質押率,則出口商要根據給定的質押率和自身的生產情況,做出最佳交貨提前期決策,進口商根據出口商的交貨提前期和自身的庫存消耗情況,做出經濟訂貨批量決策。根據供應鏈貿易流程,出口商的生產周期和進口商的庫存消耗周期有以下對應關系,如圖3所示。

圖3 出口商生產周期與進口商庫存消耗周期對應關系
由圖3可見,出口商生產周期和進口商庫存消耗周期時長相同(都為te)。進口商在si點處需要補貨,在ti點商品售罄進入缺貨狀態;出口商的庫存量在si點并未達到進口商的訂貨量Q,且海運具有一次性發貨的特殊性,因此出口商繼續生產,在te時刻達到Q后發貨,庫存水平降為0,進入第二個生產周期[te,2te]。第一批貨物在te+T時刻到達進口商處,此時交貨提前期為L=te+T-si,進口商的缺貨量為圖3中陰影部分面積,于是有:


(1)
由此可得,進口商的缺貨成本為pi(1-α)εv。
由圖3還可以得到,進口商的庫存成本為:

(2)
出口商的庫存成本為:
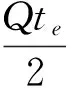
(3)
船公司的倉庫管理成本為:

(4)
假定進口商根據需求的變化調整商品的銷售價格,即需求波動前按pi的價格銷售Q-q的貨物,q為剩余質押庫存量(即質押余量),需求波動后按照pb的價格銷售q的貨物,則進口商的貨物購買成本為:
(5)
此外,根據上述參數及變量設定,進口商的海運費為ωQ,進口商的保險費為:
φ=λ(1+ξ)(piQ+ωQ)
(6)
于是,進口商的貿易總成本為:
Ci-total=Φ+pi(1-α)εv+Hi+ωQ+φ+Ci
(7)
出口商的原材料成本為paQ,融資服務費為mrpiQ。于是,出口商的貿易總成本為:
Ce-total=paQ+mrpiQ+He+Ce
(8)
船公司的海運成本為?Q,貿易總成本為:
Cs-total=Hs+?Q
(9)
根據上述成本及進口商和出口商的履約情況分析,便可求得進口商、出口商、船公司在4種雙重Stackelberg博弈策略下的利潤函數,具體如下:
在策略1下:進口商的利潤應為:
E(i)1=(pi-pe)(Q-q)-(pe-pb)q-pi(1-α)εv-hiμ-φ-ωQ-Ci
(10)
出口商的利潤應為:

(11)
船公司的利潤應為:

(12)
進口商、出口商和船公司三方的總利潤應為:

(13)
在策略2下:進口商的利潤為:
E(i)2=(pi-pe)(Q-q)-pi(1-α)εv-hiμ-φ-ωQ-Ci
(14)
出口商的利潤為:

(15)
在策略2下,由于出口商不違約,船公司也不違約,所以,船公司的利潤E(s)2與策略1下的利潤應相同,即,E(s)2=E(s)1
由此可得,在策略2下的總利潤為:

(16)
在策略3下:根據各方違約與否,可知進口商的利潤E(i)3與策略2下的利潤相同,即,E(i)3=E(i)2,出口商的利潤E(e)3與策略2下的利潤相同,即,E(e)3=E(e)2。
船公司的利潤為:

(17)
由此可得,在策略3下的總利潤函數為:

(18)
即有,策略3和策略1的總利潤函數相同。
同理,在策略4下:進口商的利潤E(i)4與策略3下的利潤相同,即,E(i)4=E(i)3;
出口商的利潤為:

(19)
船公司的利潤為:

(20)
由此可得,在策略4下的總利潤函數為:

(21)
3.3最優質押率推理
定理1策略1總優于策略2,故策略2不可行。
證明 比較策略1和策略2下的總利潤E1、E2,由式(13)和式(16)相減,可得:E1-E2=pbq>0,即E1>E2,故策略1總是優于策略2,故策略2不可行,得證。
定理1說明,在貸款期末,當質押貨物市場售價pi小于進口商與出口商簽訂的購貨價pe時,進口商違約不再提貨,船公司會選擇變賣剩余貨物q,故策略2不會出現,這也符合實際情況。因此,本文以下只需討論策略1、策略3和策略4下的質押率優化問題。
定理2當出口商給定交貨提前期L,在策略1、策略3和策略4下,進口商的最優訂貨批量Q*存在且相等。
證明 在策略1下,進口商的利潤展開式為:

(22)


(23)
則可求得進口商利潤最大時的訂貨批量Q1*為:

(24)
在策略3下,進口商的利潤展開式為:

(25)

由式(22)和式(25)相減,可得:
E(i)3-E(i)1=(pe-pb)q
(26)
根據式(26)可知,E(i)3和E(i)1只相差常數項,對E(i)3求Q的一階導數并令其為零,其結果也應為式(24)。所以,在策略3下,進口商的最優訂貨批量Q3*存在,且Q3*=Q1*。
又由于,E(i)4=E(i)3,所以,在策略4下,進口商的最優訂貨批量Q4*存在,且Q4*=Q3*=Q1*=Q*。得證。
定理3在策略1、策略3和策略4下,當進口商以最優訂貨批量決策時,出口商的最佳交貨提前期L*存在且相等。
證明 為簡便起見,令:

(27)

(28)
則式(24)可表示為:
Q*=Q1*=M+N*(s-kL)
(29)
于是,在策略1下,當進口商以最優訂貨批量決策時,則出口商利潤函數為:


(30)
可見,此時,E(e)1是關于L的一元二次函數,顯然有-(hek2)/(2P)<0,故一定存在最優的L1*,使E(e)1值最大。對E(e)1求L的一階導數并令其等于零,即:


(31)
則在策略1下,當進口商以最優訂貨批量決策時,出口商利潤最大時的交貨提前期L1*為:

(32)
同理,在策略3下,當進口商以最優訂貨批量決策時,則出口商利潤函數為:


(33)
顯然,E(e)3是關于L的一元二次函數,且-(hek2)/(2P)<0,故一定存在最優的L3*,使E(e)3的值最大。
由式(30)和式(33)相減,可得:
E(e)1-E(e)3=peq
(34)
根據式(34)可知,E(e)1和E(e)3只相差常數項,對E(e)3求L的一階導數并令其為零,其結果也為式(32)。所以,在策略3下,當進口商以最優訂貨批量決策時,出口商的最佳交貨提前期L3*存在,且L3*=L1*。
在策略4下,當進口商以最優訂貨批量決策時,則出口商利潤函數為:


(35)
顯然,E(e)4是關于L的一元二次函數,且-(hek2)/(2P)<0,故一定存在最優的L4*,使E(e)4的值最大。
由式(30)和式(35)相減,可得:
E(e)1-E(e)4=(pe-pa)q
(36)
根據式(36)可知,E(e)1和E(e)4只相差常數項,對E(e)4求L的一階導數并令其為零,其結果也為式(32)。所以,在策略4下,當進口商以最優訂貨批量決策時,出口商的最佳交貨提前期L4*存在,且L4*=L3*=L1*=L*。得證。
定理4當出口商以最優交貨提前期、進口商以最優訂貨批量決策時,最優質押率存在且可求解。
證明 當出口商以最優交貨提前期、進口商以最優訂貨批量決策時,可將式(32)代入式(29),得:




(37)
再將式(32)和式(37)代入策略1的總利潤函數式(13)中,得:


(38)
可見,E1是關于r的一元二次函數,且有:


(39)
可得在策略1下,當出口商以最優交貨提前期、進口商以最優訂貨批量決策時,使總利潤最優的質押率r1*為:

(40)
由于,E3=E1,所以,在策略3下,當出口商以最優交貨提前期、進口商以最優訂貨批量決策時,使總利潤最優的質押率r3*=r1*。
再將式(32)和式(37)代入策略4的總利潤函數式(21)中,得:


(41)
由式(41)可見,E4是關于r的一元二次函數,且有:


(42)
可得在策略4下,當出口商以最優交貨提前期、進口商以最優訂貨批量決策時,使總利潤最優的質押率r4*為:

(43)
由此可見,在策略1、策略3和策略4下的最優質押率均可求解,且r3*=r1*,故本文以下只需討論策略1和策略4下的質押率優化問題。得證。
3.4最優質押率模型
由式(13)和式(21)相減,可得:
E1-E4=(pir-pa)q
(44)
由式(44)可知,當r>pa/pi時,E1>E4;當r 圖4 總利潤函數 由圖4可見,總利潤函數是由2條開口向下的拋物線組成的分段連續性函數。 當rm>pa/pi時,即船公司設定的質押率大于pa/pi時,則有E=E1。于是,根據定理4,最優質押率為: (45) 當rw (46) 當rm≤pa/pi≤rw時,則總利潤函數由E1和E4兩部分組成,最優質押率需要進行比較后才能確定。將r1*和rw分別代入式(13)中,計算E1(r1*)和E1(rw)值;將r4*和rm分別代入式(21)中,計算E4(r4*)和E4(rm)值。比較E1(r1*)、E1(rw)、E4(r4*)和E4(rm)值的大小,找出其中最大值所對應的質押率r0,則有: (47) 3.5求解方法 由出口海陸倉融資業務流程可知,船公司設定一個質押率后,出口商則根據此質押率確定交貨提前期,進口商則再根據交貨提前期確定訂貨批量。根據上述推理分析,采用反向推理法,可設計求解最優質押率的步驟如下: ①根據定理3,得到含有r的L*表達式(32); ②根據定理2,將式(32)代入式(24),得到含有r的Q*表達式,這樣,L*與Q*都為r的函數; ③根據定理4,再將L*與Q*代入E1、E4,得到r1*式(40)和r4*式(43); ④計算r1*、r4*、pa/pi,再計算E1(r1*)、E1(rw)、E4(r4*)和E4(rm)值; ⑤比較pa/pi與rm的大小。若rm>pa/pi,執行步驟⑥,反之,進入步驟⑦; ⑥比較r1*與rm和rw的大小。根據式(45),得出最優質押率,轉入步驟⑩。 ⑦比較pa/pi與rw的大小。若rw ⑧比較r4*與rm和rw的大小。根據式(46),得出最優質押率,轉入步驟⑩。 ⑨比較E1(r1*)、E1(rw)、E4(r4*)和E4(rm)的大小,得出最大值對應的質押率r0。根據式(47),得出最優質押率,轉入步驟⑩。 ⑩輸出結果,求解步驟結束。 根據2016/02/01-2016/04/30上海期貨交易所提供的銅(cu1605)的周收盤價數據,對某出口海陸倉融資業務中銅產品進行模擬質押。假設出口商生產準備成本為24 000元/次,進口商訂貨固定成本為18 000元/次;進口商單位商品進貨價為30 000元/噸,單位商品原材料價格為27 000元/噸,處理價為28 000元/噸;出口商和進口商每單位貨物的倉儲費用分別為25元/噸/月和40元/噸/月;船公司倉庫管理費用為20元/噸/月,單位運價和海運成本分別為3 000元/噸和2 000元/噸,保險費率為0.003,保險加成率為10%,融資服務費率為4%,設定的質押率下限為10%,質押率上限為90%;出口商生產率為22 000噸/月,進口商庫存消耗速度為22 050噸/月;進口商安全庫存為1 500噸,質押余量為1000噸,給顧客的缺貨價格折扣為0.8,缺貨時愿意等待的顧客比例為0.72。 當質押貨物市場需求波動時,對其市場售價取一組不同的值,利用Matlab軟件包對該算例進行求解,得到最優質押率結果如表1所示。 由表1可見,當質押貨物市場需求波動導致市場售價變化時,均存在最優的出口海陸倉存貨融資質押率,最優質押率與最佳交貨提前期、最優訂貨批量呈負相關關系。且在其他參數不變的情況下,質押貨物市場售價越高,最優質押率越低,究其原因,是由于最優質押率等于貸款本金與質押貨物價值的比率,而質押貨物價值等于質押貨物市場售價與需求量的乘積。故在貸款本金確定的情況下,質押貨物市場售價越高,質押貨物價值就越高,最優質押率就越低。由此可見,質押貨物價格的高低是影響最優質押率變化的重要條件。 此外,下述條件變化必然會對進口商的履約產生影響,從而也會影響到船公司制定最優質押率的結果:(1)進口商進貨價變化;(2)出口商原材料購買價格變化。為驗證本文所提出模型方法的適用性和有效性,下面進一步運用敏感性分析方法探討這些條件變化對質押率優化結果的影響。圖5展示了在假定進口商市場售價為37 000元/噸的情況下,進口商進貨價變化的敏感性分析結果。 表1 市場售價不同的最優質押率、最佳交貨提前期、最優訂貨批量結果 圖5 進口商進貨價與質押率的關系 從圖5中可以看出,在其他條件不變的情況下,進口商進貨價與最優質押率正相關,然而當進貨價增加到一定程度時,質押率的變動趨于平緩,這是由于通過模型求得的質押率超過了船公司設立的質押率上限,實際融資應采用質押率上限作為最優質押率;當進貨價減少到一定程度時質押率也趨于平緩,這是由于求得的質押率小于船公司設立的質押率下限,在實際融資時應采用質押率下限作為最優質押率。 圖6展示了在進口商市場售價和進貨價都變動的情況下,最優質押率的變化情況。 圖6 進口商售價、進貨價與質押率的關系 從圖6中可以看出,在不同售價下,進口商進貨價與最優質押率都呈正相關關系,且當進貨價增加到一定程度時,質押率的變動趨于平緩,在實際融資時應采用質押率上限作為最優質押率;當進貨價減少到一定程度時質押率也趨于平緩,在實際融資時應采用質押率下限作為最優質押率。符合本文提出的質押率優化模型方法。 圖7展示了在假定進口商售價為37 000元/噸的情況下,出口商原材料購買價格變化時的敏感性分析結果: 圖7 出口商原材料購買價格與質押率的關系 從圖7中可以看出,在其他條件不變的情況下,出口商原材料購買價格與質押率負相關,當出口商原材料購買價格低至一定程度時,質押率的變動趨于平緩,這是由于通過模型求得的質押率超過了船公司設立的質押率上限,實際融資應采用質押率上限作為最優質押率;當出口商原材料購買價格增加到一定程度時質押率也趨于平緩,這是由于求得的質押率小于船公司設立的質押率下限,在實際融資時應采用質押率下限作為最優質押率。 圖8展示了在進口商市場售價和出口商原材料購買價格都變動的情況下,最優質押率的變化情況: 圖8 進口商售價、出口商原材料購買價格與質押率的關系 從圖8中可以看出,在不同售價下,出口商原材料購買價格與最優質押率都呈負相關關系,且當出口商原材料購買價格減少到一定程度時,質押率的變動趨于平緩,是由于通過模型求得的質押率超過了船公司設立的質押率上限,在實際融資時應采用質押率上限作為最優質押率;當出口商原材料購買價格增加到一定程度時質押率也趨于平緩,是由于求得的質押率小于船公司設立的質押率下限,在實際融資時應采用質押率下限作為最優質押率。符合本文提出的質押率優化模型方法。 綜上,當進口商的貨物售價、進貨價、出口商原材料購買價格發生變化時,本文提出的質押率優化模型方法仍然有效,表明該模型方法具有較好的普適性,可用于實際的海陸倉融資業務決策中。 在出口海陸倉融資業務中,需求波動會對質押貨物市值產生影響,可能導致進口商和出口商出現違約情況,而質押率優化是融資風險管理和控制決策的關鍵。本文針對需求波動條件下的出口海陸倉融資質押率優化問題,構建了質押率分段函數優化模型,在論證了質押率最優解存在的基礎上,采用反向推理法設計了求解步驟。通過設定有關參數取值,并選取2016/02/01-2016/04/30期間上海期貨交易所提供的一組銅(cu1605)周收盤價數據,利用Matlab軟件包對算例進行了求解,均可以得到船公司的最優質押率,從而驗證了模型的適用性和有效性。結果表明,船公司最優質押率與出口商最佳交貨提前期、進口商最優訂貨批量均呈負相關關系,質押貨物市場售價和出口商原材料購買價格均與最優質押率負相關,進口商進貨價與最優質押率正相關。因此,在需求不確定條件下,船公司應根據不同的博弈策略,結合出口/進口商購買和出售貨物價格的變化,設定出合理的質押率,以實現整體利益的最大化。 本文僅考慮了融資后期質押貨物市場需求變動對質押率的影響,今后將考慮延遲支付、不同博弈方法對比、風險防范等情況,對模型進一步拓展和完善。 [1] Frye J, Ashley L, Bliss R, et al. Collateral damage: A source of systematic credit risk[J]. Risk, 2000, 13(4): 91-94. [2] Cossin D, Huang Zhijiang, Auron-Nerin D, et al. A framework for collateral risk control determination[R]. Working Paper, European Central Bank, 2003. [3] Buzacott J A, Zhang R Q. Inventory management with asset-based financing[J]. Management Science, 2004, 50(9): 1274-1292. [4] Damjanovic T, Girdenas S. Quantitative easing and the loan to collateral value ratio[J]. Journal of Economic Dynamic and Control, 2014,45: 146-164. [5] 于輝, 甄學平. 中小企業倉單質押業務的質押率模型[J]. 中國管理科學, 2010, 18(6): 104-112. [6] 易雪輝, 周宗放. 雙重 Stackelberg 博弈的存貨質押融資銀行信貸決策機制[J]. 系統工程, 2012, 29(12): 1-6. [7] 李毅學, 馮耕中, 張媛媛. 委托監管下存貨質押融資的關鍵風險控制指標[J]. 系統工程理論與實踐, 2011, 31(4): 587-598. [8] 李毅學, 汪壽陽, 馮耕中. 物流金融中季節性存貨質押融資質押率決策[J]. 管理科學學報, 2011, 14(11): 19-32. [9] 張國興, 劉鵬. CERs 收益權質押融資業務的質押率模型[J]. 管理評論, 2012, 24(2): 59-64. [10] 匡海波, 張一凡, 張連如. 低碳港口物流質押貸款組合優化決策模型[J]. 系統工程理論與實踐, 2014, 34(6): 1468-1479. [11] 匡海波, 張一凡, 張連如. 低碳港口存貨質押貸款利率定價理論和模型[J]. 中國管理科學, 2014, 22(12): 1-10. [12] 嚴飛, 汪傳旭. 海陸倉融資模式下船公司質押率優化[J]. 上海海事大學學報, 2010, 31(1): 47-55. [13] 嚴飛, 汪傳旭. 貨價呈現布朗運動規律的海陸倉融資收支利率優化研究[J]. 復旦學報(自然科學版), 2011, 50 (1): 114-120. [14] 潘意志, 袁澄清, 潘志明. 海陸倉質押融資貸款模式若干問題分析[J]. 港口經濟, 2013 (3): 13-17. [15] 王功榮, 曾誠, 胡正偉. 航運企業在“海陸倉”融資方式中的法律風險及防范[J]. 中國海商法研究, 2013, 24 (3): 109-115. [16] 廖鑫凱, 趙波, 許仲生. “出口海陸倉”供應鏈融資模式探析[J]. 青島遠洋船員職業學院學報, 2012, 33 (1): 30-34. OptimizationonLoan-to-valueRatiosofExportingOffshore/In-transitInventoryFinancing WANGZi-cheng1,ZHOUYong1,YANGHua-long1,2 (1.Transportation Management College, Dalian Maritime University, Dalian 116026, China;2.Collaborative Innovation Center for Transport Studies,Dalian Maritime University,Dalian 116026,China) Exporting offshore/in-transit inventory financing means that the bank regards the shipping company's credit guarantee as a condition, and commissions the shipping company to supervise and transport pledged goods throughout the entire journey (offshore warehouse, in transit, to the destination warehouse). It's a new inventory mortgaging/financing mode with worldwide credit, which can not only relieve exporters in terms of a shortage of funds, but can also bring new types of profit growth points for banks and shipping companies. Exporting offshore/in-transit inventory financing has practical significance for promoting the development of seaborne trade and supply chain finance. The optimization of its loan-to-value ratio, namely the ratio of loan principal and the value of the pledged goods, is the key to manage and control the risk. 1003-207(2017)10-0020-11 10.16381/j.cnki.issn1003-207x.2017.10.003 F 830.56 A 2015-07-31; 2016-08-16 國家自然科學基金資助課題(71372088);中央高校基本科研業務費(01760431);遼寧省高等教育內涵發展專項資金(協同創新中心)資助項目(20110116102) 楊華龍(1964-),男(漢族),遼寧大連人,大連海事大學交通運輸管理學院教授,博士生導師,研究方向:物流與供應鏈管理,E-mail:hlyang@dlmu.edu.cn. According to the process of exporting offshore/in-transit inventory financing,the trading decisions of the shipping company, exporter and importer reflect the relationship of a double Stackelberg Game strategy. The first game occurs between the shipping company and exporter. The shipping company sets the loan-to-value ratiorfirst, and then the exporter determines the delivery lead timeLaccordingly. Therefore, the shipping company is the leader, and the exporter is the follower in the game. The second game takes place between the exporter and the importer. The exporter sets the delivery lead timeLfirst, and then the importer determines the order quantitiesQaccordingly. Therefore, the exporter is the leader and the importer is the follower in the game. In international seaborne trade, demand fluctuations will affect the value of pledged goods, which may result in non-compliance. When the market price of the pledged goods is higher than the purchase price signed by the importer and exporter, the importer will withdraw the pledged goods normally. Otherwise, the importer and exporter are likely to default, so the shipping company could sell the collateral to make up the loan capital. In this paper, the issue of optimization on loan-to-value ratios of exporting offshore/in-transit inventory financing under uncertain demand is addressed. Based on the theory of double Stackelberg game, the total profit functions under four game strategies among the shipping company, exporter and importer are analyzed and constructed, aiming at maximizing the total profit of the supply chain. The piecewise function optimization model of loan-to-value ratios is established. The existence of optimal loan-to-value ratios is proved. A reverse reasoning method is adopted to solve the model. The solution process is designed as follows: firstly, maximize the profit of the exporter to get the expression of the best delivery lead timeL*containingr, secondly, maximize the profit of the importer to get the expression of the economic ordering quantityQ*containingL*, then the optimal loan-to-value ratior*is solved by maximizing the total profit function. Numerical example is used to verify the applicability and validity of the proposed model. The results indicate that the optimal loan-to-value ratio has a positive correlation with the importer's purchase price, and has a negative correlation with the market price and raw material price of pledged goods, respectively. Therefore, the shipping company should keep a close eye on the price changes of pledged goods, and set a reasonable loan-to-value ratio to increase the total profits of the supply chain. The findings can provide scientific guidance for the optimization of exporting offshore/in-transit inventory financing. Keywords: exporting offshore/in-transit inventory; financing; loan-to-value ratio; double Stackelberg Games; reverse reasoning method
4 算例分析

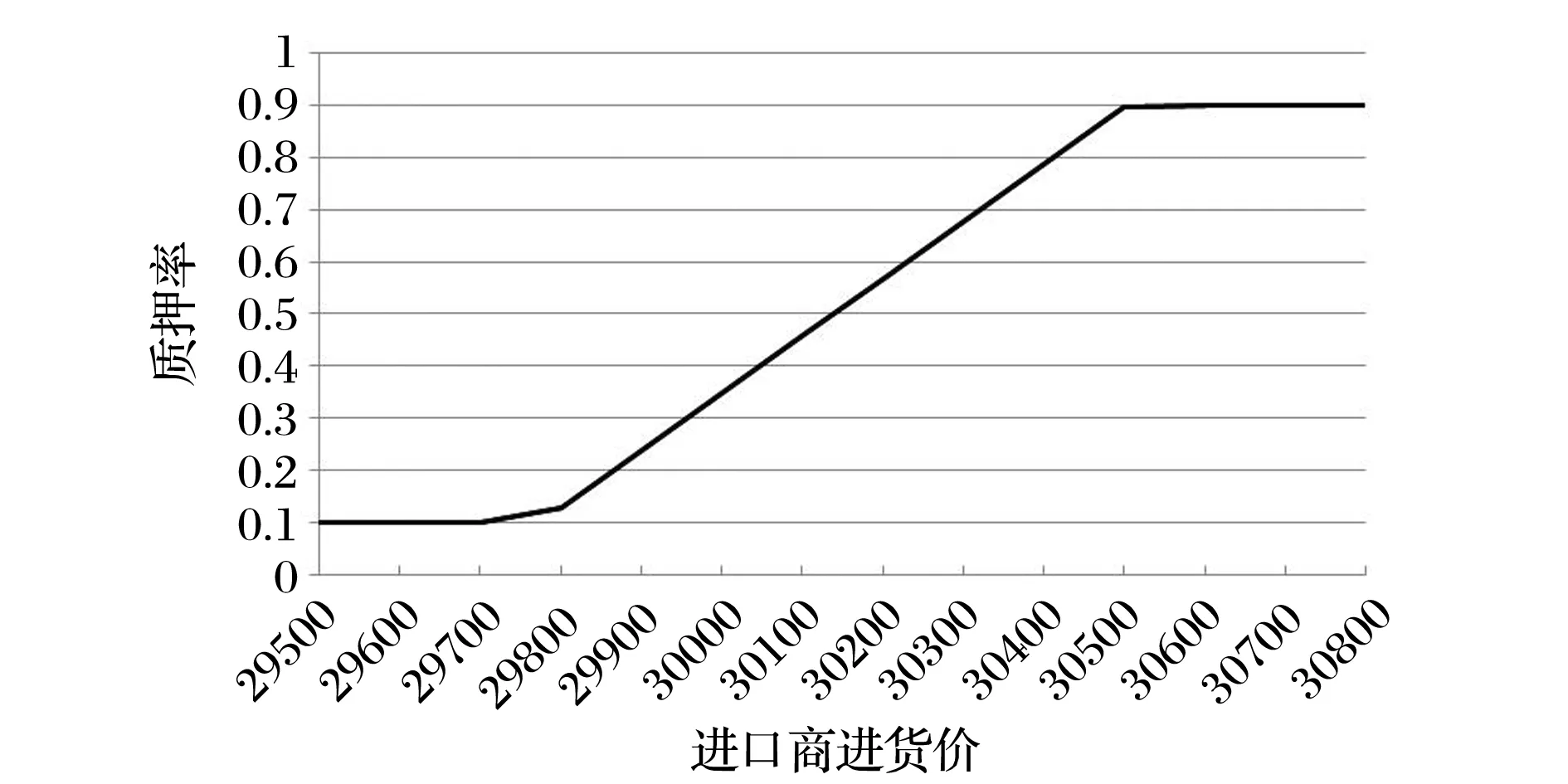



5 結語

