微課引路 互動通幽 理解建構(gòu)

朱成燈

[摘 要] “農(nóng)村初中數(shù)學(xué)微媒體下互動學(xué)習(xí)模式研究”課題組自2016年9月開始實踐和研究以來，取得一系列成果，本文結(jié)合“弧長及扇形的面積”的教學(xué)，對“三學(xué)互動”課堂教學(xué)模式下的公式教學(xué)進行初步梳理和反思：微課引路；互動通幽；理解建構(gòu).

[關(guān)鍵詞] “三學(xué)互動”；理解建構(gòu)；公式教學(xué)

2016年度福建省基礎(chǔ)教育課程教學(xué)研究規(guī)劃立項課題“農(nóng)村初中數(shù)學(xué)微媒體下互動學(xué)習(xí)模式研究”自2016年9月開題以來，按計劃扎實開展研究，取得階段性的成果. 2017年2月22日，課題組在筆者所在學(xué)校開展“三學(xué)互動”課堂教學(xué)模式專題研訓(xùn)活動，推進了課題研究的進程. 筆者作為課題組的核心成員，利用“三學(xué)互動”課堂教學(xué)模式設(shè)計的“弧長及扇形的面積”得到大家的肯定和贊賞. 下面結(jié)合教學(xué)案例對“三學(xué)互動”課堂教學(xué)模式下如何開展公式教學(xué)進行簡單介紹，并對其設(shè)計思路進行梳理和反思.

教學(xué)分析

1. 教學(xué)背景

（1）標準分析

《全日制義務(wù)教育數(shù)學(xué)課程標準》（2011版）（以下簡稱《標準》）對本節(jié)課教學(xué)內(nèi)容的要求如下：會計算圓的弧長、扇形的面積.可以看出“會”的同類詞是“理解”，是描述結(jié)果目標的行為動詞，即“描述對象的特征和由來，闡述此對象與相關(guān)對象之間的區(qū)別和聯(lián)系”，因此，在教學(xué)過程中應(yīng)引起教師的足夠重視.

（2）教材分析

本節(jié)課的教學(xué)內(nèi)容是北師大版數(shù)學(xué)九年級下冊第三章“圓”中的第九節(jié)“弧長和扇形的面積”. 這是在小學(xué)已學(xué)習(xí)圓周長和面積計算、扇形的簡單知識和在前階段學(xué)完了與圓有關(guān)的知識的基礎(chǔ)上進一步探究弧長公式和扇形面積公式的推導(dǎo)過程及其在實際問題中的應(yīng)用，是圓的有關(guān)計算中的一個重要問題，應(yīng)讓學(xué)生感受類比、從特殊到一般的數(shù)學(xué)思想方法，并為學(xué)生今后的學(xué)習(xí)及生活更好地運用數(shù)學(xué)做準備.

（3）學(xué)情分析

學(xué)生已經(jīng)學(xué)習(xí)了圓的有關(guān)基礎(chǔ)知識，有一定的知識水平和自主學(xué)習(xí)、解決問題的能力，但是筆者所在學(xué)校是一所農(nóng)村中學(xué)，學(xué)生的數(shù)學(xué)學(xué)習(xí)水平參差不齊，大多數(shù)學(xué)生對數(shù)學(xué)的理解僅僅停留在計算和直接套用公式的水平，對稍難的數(shù)學(xué)問題缺乏深入思考和探索的勇氣. 因此，在教學(xué)中，筆者鼓勵并引導(dǎo)學(xué)生進行預(yù)學(xué)、獨立思考、合作互助、循序漸進，進一步探究弧長及扇形面積的計算公式和運用公式解決實際問題.

2. 教學(xué)目標

結(jié)合《標準》和教材結(jié)構(gòu)與內(nèi)容，考慮到學(xué)生已有的認知結(jié)構(gòu)和心理特征，制訂如下教學(xué)目標.

知識與技能：能推導(dǎo)，并熟記弧長、扇形面積的計算公式，理解公式中每個字母的含義，并能應(yīng)用公式進行計算.

過程與方法：經(jīng)歷用類比、聯(lián)想的方法探索弧長計算公式和扇形面積計算公式的過程，培養(yǎng)學(xué)生的自主探索能力.

情感態(tài)度與價值觀：通過預(yù)學(xué)、研學(xué)、助學(xué)，激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，提高其學(xué)習(xí)積極性.

3. 教學(xué)重、難點

從《標準》出發(fā)，在吃透教材的基礎(chǔ)上，確立了如下教學(xué)重點、難點.

重點：弧長、扇形面積計算公式的推導(dǎo)，并能應(yīng)用公式進行計算.

難點：弧長和扇形面積計算公式的靈活運用.

4. 教法、學(xué)法

采用“三學(xué)互動”課堂教學(xué)模式，即讓學(xué)生通過課前個體預(yù)學(xué)、集體研學(xué)、群體助學(xué)，經(jīng)歷數(shù)學(xué)公式發(fā)生、發(fā)展、形成的“再創(chuàng)造”活動，獲取廣泛的數(shù)學(xué)活動經(jīng)驗，進而促進自身的發(fā)展.

凸顯學(xué)生主體地位：學(xué)生根據(jù)教師給出的任務(wù)清單，自主、主動地思考，尋找解決問題的途徑，完成教材閱讀、解讀微課（視頻）、當(dāng)堂測試，并歸納和梳理知識的特點、知識間的聯(lián)系.

明晰教師主導(dǎo)作用：教師根據(jù)學(xué)生思維的起點預(yù)設(shè)問題，及時掌握課堂上生成的問題和存在的問題，針對性地組織研學(xué)、助學(xué)答疑解惑、歸納梳理.

教學(xué)過程

（一）第一環(huán)節(jié)：微課引路，個體預(yù)學(xué)

師生活動：課前，教師認真解讀教材內(nèi)容，根據(jù)學(xué)生實際認知水平制作《弧長的計算公式煉成記》微視頻和學(xué)習(xí)任務(wù)單等學(xué)習(xí)材料，學(xué)生觀看微視頻進行自主學(xué)習(xí)，邊看邊思考，完成學(xué)習(xí)任務(wù)單，并在學(xué)習(xí)過程中記錄重要知識、方法和困惑.

學(xué)習(xí)任務(wù)單

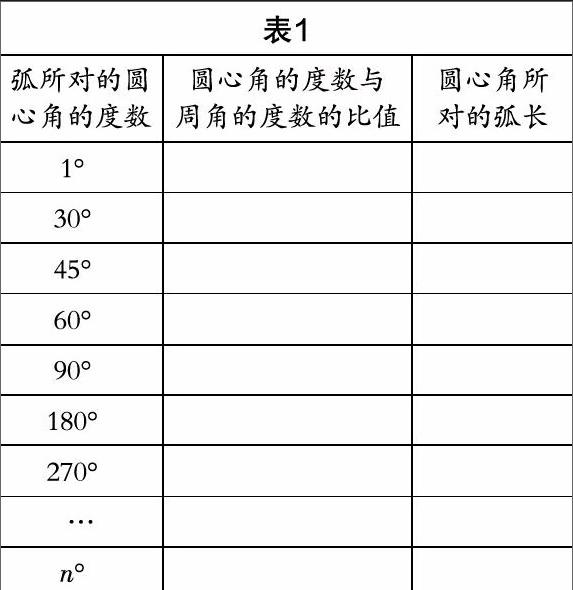
1. 半徑為R的圓，周長是多少？圓可以看作是幾度圓心角所對的弧？

2. 完成下面的表格.

（二）第二環(huán)節(jié)：探索新知，集體研學(xué)

1. 探究弧長計算公式

活動1：建構(gòu)弧長計算公式

師生活動：學(xué)生相互交流自學(xué)中遇到的困惑. 教師巡查并參與交流，掌握學(xué)生的預(yù)學(xué)情況. 針對存在的疑惑，組織學(xué)生進行集體研討，請預(yù)學(xué)充分的同學(xué)到講臺前展示，其他學(xué)生補充，教師適當(dāng)點撥或有針對性地講解. 通過討論得到結(jié)論：圓心角對于周角，弧長對于圓周長，都是部分對于整體的關(guān)系，弧所對的圓心角是周角的幾分之幾，那么弧長就是圓周長的幾分之幾，所以弧所對的圓心角與周角的比值等于它與圓周長的比值，用這個比值乘以圓周長就能

設(shè)計意圖 教師根據(jù)學(xué)生的預(yù)學(xué)情況，對學(xué)生生成的問題、存在的問題精心設(shè)計數(shù)學(xué)活動，組織學(xué)生集體研討，暴露思維過程，分享所思所想的成果. 教師對重難點知識進行指導(dǎo)性梳理，基于部分對于整體的關(guān)系，體會從特殊到一般再到特殊的認知過程，自主建構(gòu)出弧長計算公式. 這樣能喚起學(xué)生的參與意識、問題意識，產(chǎn)生探究交流的學(xué)習(xí)渴望. 師生、生生之間互動研學(xué)、交流溝通，多次思維碰撞、反思，這樣獲得的知識會更深刻，也會為下面探究扇形的面積公式打下基礎(chǔ).

活動2：應(yīng)用弧長計算公式

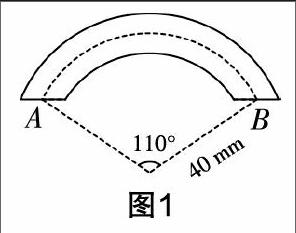
例題 制作彎形管道時，需要先按中心計算“展開長度”再下料. 如圖1，試計算圖中所示的管道的展直長度，即弧AB的長（結(jié)果精確到0.1 mm）.

練習(xí) （1）已知扇形的圓心角為45°，半徑長為12 cm，求該扇形的弧長.endprint

（2）如果一條弧的長是π，半徑是6，求這條弧所對的圓心角度數(shù).

（3）求圓心角為120°、弧長為12π的弧的半徑.

師生活動：學(xué)生先獨立思考，接著同桌交流，最后進行全班展示. 教師進行適時評價和點撥，并強調(diào)：在應(yīng)用弧長公式進行計算時，要注意公式中n的意義.

設(shè)計意圖 通過例題和練習(xí)的剖析，在加深對弧長公式的理解基礎(chǔ)上，學(xué)生學(xué)會表達和交流，并學(xué)會創(chuàng)新應(yīng)用弧長計算公式，熟練掌握公式中l(wèi)，R，n三個量之間的換算關(guān)系，滲透方程思想.

2. 探究扇形的面積公式

活動1：建構(gòu)扇形的面積公式

（1）教師引導(dǎo)學(xué)生類比探索弧長公式的方法，合作互助探究扇形面積公式.

（2）比較扇形面積公式和弧長公式，如何用弧長和半徑表示扇形的面積？

設(shè)計意圖 有了前面對弧長計算公式的探究，用部分和整體的思想，再去推導(dǎo)扇形面積公式，就迎刃而解了.在推導(dǎo)扇形面積計算的第二種方法時，要關(guān)注多種推導(dǎo)方法，鍛煉學(xué)生探索新知識的能力，讓其體驗成功的快樂，形成類比思維能力.

活動2：應(yīng)用扇形的面積公式

（1）課本第101頁例2.

（2）已知扇形的圓心角為60°，扇形的面積為24π，則這個扇形的半徑是多少？

（3）已知扇形的半徑為2，扇形的面積為π，則這個扇形的圓心角是多少？

設(shè)計意圖 通過練習(xí)，學(xué)生能熟練掌握扇形面積公式中S，R，n三個量的轉(zhuǎn)化關(guān)系，只要知道其中兩個就可以求第三個，滲透方程思想.

（三）第三環(huán)節(jié)：鞏固提升，群體助學(xué)

活動內(nèi)容：（1）如果扇形的半徑為9，弧長為4π，那么扇形的面積是______.

（2）在田徑二百米跑比賽中，有一段彎道是圓弧形的，它的半徑為20米，所對的圓心角是90°，你能求出這段彎路的展直長度嗎？ （π取3.14）

（3）已知圓上一段弧長為240π，半徑為180，則這段弧所對的圓心角的度數(shù)是______.

（4）如圖2，以等邊三角形ABC的三個頂點為圓心、2為半徑作圓，則圖中陰影部分的面積是______.

師生活動：學(xué)生先獨立思考，小組合作互助完成上面4個問題. 教師巡視，發(fā)現(xiàn)學(xué)生存在的典型錯誤，用投影儀展示部分學(xué)生有代表性的作品，并適時點評. 學(xué)生集體交流訂正答案后互講，并進行解后反思.

設(shè)計意圖 這四道習(xí)題涵蓋本節(jié)的知識點、疑難點、關(guān)鍵點，并且從易到難，注重考查學(xué)生對其中所蘊含的數(shù)學(xué)本質(zhì)的理解，對學(xué)生基礎(chǔ)知識和基本技能達成情況進行評價. 通過教師助學(xué)、學(xué)生一對一的互助學(xué)習(xí)，能及時解決學(xué)生存在的問題，力爭做到“題題清、堂堂清、人人清”.

（四）第四環(huán)節(jié)：課堂反思，總結(jié)歸納

師生活動：教師引導(dǎo)學(xué)生回顧“弧長和扇形面積公式怎么來”“怎么記”“怎么用”，以及所包含的數(shù)學(xué)思想. 教師根據(jù)情況進行補充、糾正或點評，出示知識體系，并強調(diào)知識的重難點，及時激勵表現(xiàn)好的學(xué)生，樹立典型，使學(xué)習(xí)氛圍更加和諧.

設(shè)計意圖 引導(dǎo)學(xué)生在總結(jié)知識點的同時，注意推導(dǎo)數(shù)學(xué)公式的學(xué)習(xí)過程和所涉及的數(shù)學(xué)思想方法，學(xué)會表達和交流，使學(xué)生真正學(xué)會學(xué)習(xí)，提高分析、歸納、總結(jié)的能力.

（五）第五環(huán)節(jié)：課后作業(yè)

必做：課本第102頁第1、2、3題.

選做：課本第102頁第4題.

設(shè)計意圖 對作業(yè)進行分層，對不同的學(xué)生提出不同的要求，使“人人都能獲得良好的數(shù)學(xué)教育，使不同的人在數(shù)學(xué)上得到不同的發(fā)展”，從作業(yè)中了解學(xué)生基礎(chǔ)知識與基本技能的掌握情況.

（六）第六環(huán)節(jié)：板書設(shè)計

設(shè)計意圖 在多媒體的教學(xué)下，結(jié)構(gòu)清晰、重點突出的板書具有不可替代的作用. 必要的板書有利于實現(xiàn)學(xué)生的思維與教學(xué)過程同步，有助于學(xué)生更好地把握教學(xué)內(nèi)容脈絡(luò).

感悟與反思

1. 微課引路，個體預(yù)學(xué)

傳統(tǒng)的數(shù)學(xué)公式教學(xué)大多是教師講解、學(xué)生聽練的模式，停留在機械記憶、反復(fù)操練公式上，而對公式的形成過程不夠重視. 其實，數(shù)學(xué)公式教學(xué)應(yīng)該讓學(xué)生經(jīng)歷公式的形成過程，揭示公式的本質(zhì)，掌握公式的結(jié)構(gòu)特征. 在課堂教學(xué)中，受制于教學(xué)內(nèi)容和時間，教師難以用大量的時間實施探究，因此，我們認為微課導(dǎo)學(xué)無疑是一種有效的途徑，能給學(xué)生自主預(yù)習(xí)提供十分便利、快捷的學(xué)習(xí)環(huán)境. 本節(jié)課教學(xué)前，筆者精心制作符合學(xué)生認知水平的短小精悍的微視頻——《弧長的計算公式煉成記》，配上2017年最火的民謠《成都》的伴奏音樂，為學(xué)生的預(yù)學(xué)創(chuàng)設(shè)生動活潑的教學(xué)情境. 課前，學(xué)生根據(jù)學(xué)習(xí)任務(wù)單，通過閱讀教材內(nèi)容進行文本預(yù)學(xué)，同時觀看微視頻，思考教師推送的預(yù)設(shè)問題，將困惑的、不理解的問題記錄下來. 經(jīng)歷了再現(xiàn)弧長的計算公式的探索過程，學(xué)生積極主動地參與高層次思維的過程性學(xué)習(xí)活動，感悟到部分與整體的思想，自主生成、主動建構(gòu)了弧長的計算公式，積累活動經(jīng)驗，內(nèi)化知識間的聯(lián)系，前后連貫，使后面對扇形的面積公式的探究水到渠成.

2. 互動通幽，意外精彩

在建構(gòu)扇形的面積公式活動中，通過集體交流討論，學(xué)生1指出：要求扇形的面積，可以先求圓的面積，再乘一個分數(shù)，這個分數(shù)就是圓心角的度數(shù)與周角的比值. 這一推導(dǎo)過程涵蓋整式、分式的運算，對運算的基本技能要求較高. 師生互動、生生互動、生動活潑的課堂氛圍和有效的學(xué)習(xí)活動，喚起了學(xué)生的參與意識、問題意識，暴露了其思維過程，分享其所思所想的成果，使得學(xué)生對知識的理解更深刻，生成不期而遇的精彩. 筆者為精彩生成喝彩，又及時因勢利導(dǎo)，讓學(xué)生經(jīng)過對比、思考，總結(jié)出一個更具有普遍性的規(guī)律：在同圓中，圓心角的度數(shù)與周角的比值、圓心角所對的弧長與圓周長的比值、扇形面積與圓面積的比值是相等的. 這種部分與整體的關(guān)系是弧長、扇形面積有關(guān)計算的重要依據(jù)和數(shù)學(xué)思想，能使教學(xué)活動收到較好的效果.

結(jié)束語

“三學(xué)互動”課堂教學(xué)模式是數(shù)學(xué)教學(xué)內(nèi)容與信息技術(shù)有機融合的產(chǎn)物，通過個體預(yù)學(xué)、集體研學(xué)、團體助學(xué)，完成所需知識的三次內(nèi)化，形成學(xué)習(xí)共同體. 學(xué)生逐步學(xué)會學(xué)習(xí)、學(xué)會探究、學(xué)會合作、學(xué)會創(chuàng)造，這是農(nóng)村學(xué)校提高課堂教學(xué)效益的有效途徑. 當(dāng)然，教學(xué)是一門藝術(shù)，不應(yīng)當(dāng)也不能僅依賴一種教學(xué)方式來涵蓋它的全部功能. 在實際教學(xué)活動中，教師應(yīng)注重學(xué)生的認知水平，根據(jù)課型和教學(xué)內(nèi)容、教學(xué)條件等因素，采用各種教學(xué)方式的優(yōu)勢與之深度融合，相互補充，相得益彰，形成自如駕馭課堂的教學(xué)風(fēng)格.endprint