參悟課程目標 提升教學實效

湯雙

[摘 要] 新課程改革背景下，如何提升初中數(shù)學教學效果一直困擾著一線教師. 本文以教學實錄為例，從教學藝術、質化藝術、衍生藝術三方面闡述了提升教學效果的具體做法，讓學生充分感受學習之樂，領略成長之美.

[關鍵詞] 參悟；提升；課程目標；教學實效

近期，筆者有幸參加南通市名師培養(yǎng)梯隊成員會課活動，聽了吳老師一堂新授課“平行四邊形”. 吳老師嚴謹?shù)闹螌W態(tài)度、精湛的教學技藝和與時俱進的教學理念都讓筆者深深折服，也激發(fā)了筆者對這堂課的思考.

【教學實錄片斷1】

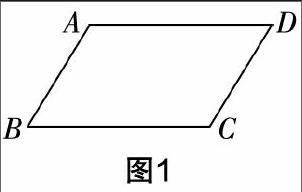
師：同學們，這是一個什么圖形？（投影圖1）

生（齊）：平行四邊形.

師：我們看一看圖1中平行四邊形的組成元素有哪些.

生1：有點和線.

師：能說得具體點嗎？

生1：有頂點.

師：對，這個多邊形有頂點，分別是點A、點B、點C、點D，還有呢？

生2：它有四條邊，分別是AB，BC，CD，DA，兩組邊互相平行，像AB∥DC.

生3：它有兩組對角，它們分別相等.

師：很好. 圖1中有四個角，分別是∠A，∠B，∠C，∠D，它們是四邊形的4個內角. 剛才，生3提到兩角的位置關系，例如∠A和∠B是……

生（齊）：同旁內角.

師：在平行線中，當兩條平行線被第三條直線所截時，會出現(xiàn)同旁內角（如圖1中的∠A和∠B）. 但在平行四邊形中，我們也把∠A和∠B稱為鄰角，圖1中這樣的鄰角還有……

生（齊）：∠B和∠C，∠C和∠D，∠D和∠A.

師：兩角之間還有其他的位置關系嗎？例如∠A和∠C是什么角？

生（齊）：對角.

師：對，這些是我們學過的知識. 今天，我們一起來進一步探究平行四邊形的性質.

師：研究一個圖形，我們第一步要給它下一個……

生（齊）：定義.

教學藝術

學生是學習的主體，教為學服務. 要實現(xiàn)這一目標，教師必須有扎實的基本功，有能靈活調控課堂教學的能力，以及能對學生的學習狀態(tài)進行準確判斷. 小學課本對平行四邊形已有介紹，學生都認識它，只是不知道平行四邊形的規(guī)范化定義，以及如何用符號語言表示出來. 鑒于此，筆者認為本節(jié)課的開場可以這樣設計：

先畫一個圖形——平行四邊形，“同學們，你們認識這個圖形嗎？”“認識，是平行四邊形. ”“你知道什么是平行四邊形嗎？”（師生共同討論，得出定義）“借用它的定義和符號表示，你知道平行四邊形有哪些性質嗎？”“對邊平行，對邊相等.”“對角相等.”如此，性質便全變成了幾何語言.

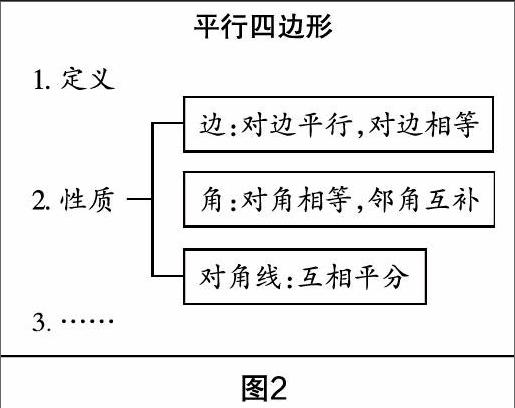
板書設計方面，豎著依次寫，條理會更清晰（如圖2），師生討論時學生提到哪一點，就板書哪一點，一方面，針對性強，能體現(xiàn)“學生是主體，我為學生服務”的理念；另一方面，是教學生學習新知的方法，為后續(xù)研究特殊的平行四邊形做鋪墊.

質化藝術

現(xiàn)在，課堂教學講求高效，那什么是高效？筆者的理解是，以最少的時間獲得最大的收獲. 那什么是收獲？課堂教學的收獲不單純體現(xiàn)為數(shù)學知識的拓展與延伸，不單純地為數(shù)學方法的掌握與應用，還涵蓋學習技能的習得. 那怎樣做才能使學生的收獲達到最大呢？筆者認為到達學生的最近發(fā)展區(qū)就是最大. 即教學中用最少的時間，使知識、方法、能力、情感、態(tài)度都達到任教班級學生的最近發(fā)展區(qū)，產生課堂教學效益.

【教學實錄片斷2】

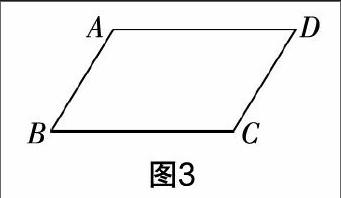
師：學習了平行四邊形的定義，請同學們看下面這個問題（投影）. 如圖3，已知四邊形ABCD是平行四邊形，若∠B=50°，求其他三個角的度數(shù)；若∠B=70°，求其他三個角的度數(shù)；若∠B=α，求其他三個角的度數(shù).

師：同學們試一試，并把你的解答過程說給大家聽.

生1：由已知，因為四邊形ABCD是平行四邊形，所以AD∥BC. 所以∠A+∠B=180°. 因為∠B=50°，所以∠A=180°-50°=130°. 又因為AB∥CD，∠B=50°，所以∠C=180°-50°=130°. 用同樣的方法可求出∠D=50°.

師：非常好！如果∠B=70°，其他三個角的度數(shù)又是多少？

生2：……

師：剛才兩題中的角是具體值，如果∠B=α，其他三個角的度數(shù)如何求？

生3：因為四邊形ABCD是平行四邊形，∠B=α，所以∠B=∠D. 所以∠D=α.

師：∠B=∠D是你算出來的嗎？

生（齊）：因為對角相等.

師：你發(fā)現(xiàn)了對角相等？為什么？

……

探究平行四邊形邊與角的性質時，吳老師尊重學生的認知規(guī)律，注重知識的生成，用建構思想指導教學，這種教學設計很好. 不過，對于第三小問“當∠B=α時，求其他三個角的度數(shù)”，此時既然學生已經(jīng)發(fā)現(xiàn)平行四邊形的對角相等，筆者覺得后面的教學過程可以質化一下. 比如，接著學生的思路，“我們今天這節(jié)課就是證明平行四邊形的對邊、對角為什么相等. ”也可以：“同學們，現(xiàn)在我們已經(jīng)認識了平行四邊形的基本元素，有四個角，四條邊，就現(xiàn)有的元素請大家從數(shù)量關系與位置關系來考量，看看它們之間有怎樣的結論，猜想并證明. ”如此一番，學生便馬上“上車”了，教學效益生成.

衍生藝術

“授人以魚，不如授人以漁. ”這是教學的終極目標，也是教育價值最大化的體現(xiàn). 本課中，平行四邊形的性質源于定義的兩個特征. 抓住這兩點指導學生探究，還可以教會學生研究平行四邊形的方法：連接其中一條對角線，將四邊形變?yōu)閮蓚€三角形，進而將研究四邊形的邊、角關系問題轉化為研究三角形的邊、角關系問題. 如果往更深一層研究，可以借助電子白板設計教學：利用電子白板“連一連”的功能，在平行四邊形內作一條輔助線或兩條輔助線，先證平行線間的兩個三角形兩兩全等，并提問“為什么平行四邊形有這些性質？”答案顯然是因為有“兩組對邊分別平行”這個前提條件. 再利用電子白板將這個圖形繞著對角線的交點旋轉180°，此時會發(fā)現(xiàn)圖形又繞回去了，這說明平行四邊形還是中心對稱圖形，這便進一步向學生滲透了中心對稱的知識.

現(xiàn)在的課堂，多媒體技術輔助課堂教學越來越廣，教學時，通過多媒體動態(tài)直觀地呈現(xiàn)平行四邊形的性質，既能加強學生對平行四邊形性質的理解，又能激發(fā)學生的學習興趣，增強課堂的趣味性.endprint