設計聯想型問題，培養學生聯想思維能力

周曉芳

[摘 要] 數學聯想，作為數學發現和數學解題的一種重要的常用方法，不僅有助于學生加深對數學概念、公式、定理的理解，還可以增強學生發散思維的能力，培養他們思維的靈活性和廣闊性，激發他們發現新事物，創造新知識的興趣，同時可以發展和提高他們的數學解題能力和應變能力，從而提高學生的數學素養.

[關鍵詞] 數學教學；聯想思維；數學素養

巴甫洛夫認為：“一切教學都是各種聯想的形式. ”而數學聯想，作為數學發現和數學解題的一種重要的常用方法，不僅有助于學生加深對數學概念、公式、定理的理解，還可以增強學生發散思維的能力，培養他們思維的靈活性和廣闊性，激發他們發現新事物，創造新知識的興趣，同時可以發展和提高他們的數學解題能力和應變能力，從而提高他們的數學素養. 所以在數學教學中，尤其是解題教學中我們必須靈活運用甚至是孕育一些聯想思維，根據所教授的內容進行一些聯想型例題與練習，“有的放矢”地培養學生的聯想思維的能力. 新課程標準規定，我們在教學過程中要形成解決問題的一些策略，體驗解決問題策略的多樣性，發展實踐能力與創新精神.

設計類比聯想問題，培養數學

聯想思維的廣闊性

例如：代數教學中對于分數的四則運算法則與分式的四則運算法則可做類比聯想，整式四則運算中的乘法亦可與有理數運算的乘法算律做類比聯想；相似三角形的性質與條件可與全等三角形的教學做類比聯想；函數教學中可相應地采取對圖形與解析式做類比聯想及推理. 另外，幾何教學中，命題、定理之間的類似，公式、法則、方法之間的相似類比更是比比皆是. 多年的教學經驗告訴筆者，教學中重視相關知識的類似性，積極引導學生做類比聯想，不僅可以鞏固學生對新舊知識的聯系，還有利于學生構建新的知識體系，從而提高學生對數學整體的理解與把握，同時幫助學生利用類比聯想探索新知識，培養與發展他們的數學聯想思維能力.

如代數教學中會不時地接觸下面一個類型的題目：已知（2x-y）2+4x-3y-1=0，求x，y的值. 學生初次接觸該題似乎有點手足無措，因為不知已知條件如何應用. 這就需要教師在教學時引導學生進一步探究，啟發學生積極活潑的思維，將“陌生”的已知條件類比為熟悉的題設條件，從而打開學生的思路之門. 初步嘗試如下：由于（2x-y）2和4x-3y-1均表示為非負數，這就可以比作兩個人口袋里的錢，當兩者和為零時，那么必須兩者同時為零，即（2x-y）2=0且4x-3y-1=0，組合可得到方程組：2x-y=0，4x-3y-1=0，解二元一次方程組本就是學生熟悉且能理解掌握的知識點，這樣尋求x，y的解就不是難事了. 當然，當題目中非負數的個數增多時，學生會類比聯想為多個“沒錢人上街”的情況，解答本類題目就無須教師反復強調分析了. 可見，類比聯想可使學生學會透過數學問題的現象揭示本質含義，也使教師達到“傳道”“解惑”的目的.

設計關系聯想型問題，提高數

學聯想思維的縝密性

關系聯想，即由事物之間的某種關系而引起的聯想. 例如因果關系、特殊與一般的關系、部分與整體的關系等均能構成關系聯想. 其中因果關系的聯想在初中數學教學中尤為廣大師生重視，它是指由事物的起因想到結果或由結果想到起因的聯想，這在初中平面幾何探索與論證中尤為顯現.

本題教師設計講解時重點引導學生觀察、聯想、歸納，然后是演繹. 聯想時對與題目中由數字向字母的過渡，教師可引領他們的呼應關系，學生對題的興趣加深、加濃，就不難找到解題的途徑與答案了.

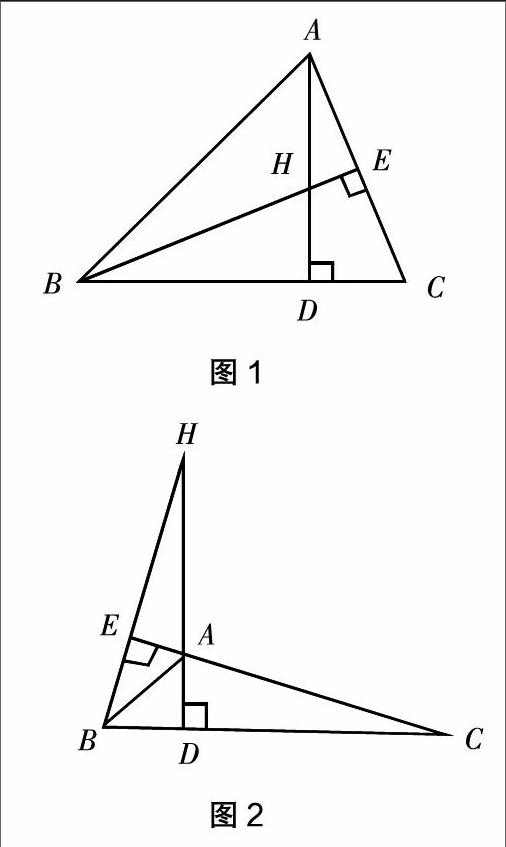
再如，已知：如圖1，在△ABC中，∠ABC=45°，H 是高AD 和BE的交點. （1）求證：BH =AC；（2）如圖2，將∠BAC 改變成鈍角時，題設條件不變，結論BH=AC能否成立？

第一小題，△ABC是個常規銳角三角形，屬于學生思維范疇內，學生不難通過三角形全等結論，證明全等的條件中，教師需要略作引導的是∠CAD與∠CBE都是∠C的余角，從而這兩個角相等. 第二小題，∠BAC變成了鈍角，從圖形的解讀看來，圖形變得略復雜，部分學生會出現“發呆”現象. 我們說，數學探索解答題的構造有它內在的關聯，不僅是題目的題設與結論甚至是探索論證的思路與過程都有其必然的相似或是相同. 所以教師在設計講解時應引導學生對第一小題結論與證明方法進行聯想，進而在圖2中聯系題設的變更，引導推理過程的演變，讓學生由全等聯想相似的結論，再執果索因，導入最后的解題方法與結論. 可見解題時讓學生自行前后對照、驗證相關結論，通過豐富的聯想活動，最終就不難得到正確的解答了. 可以說，該題成功的教學活動既加強了學生對題型的記憶，又培養和提高了學生解決數學變更問題的能力. 當然，解題的成功源自于“關系聯想”邏輯遞推的紐帶作用.

設計反向聯想型問題，加強數

學聯想思維的靈活性

反向聯想，即由一個事物聯想到與其相反、相對特點的另一事物.

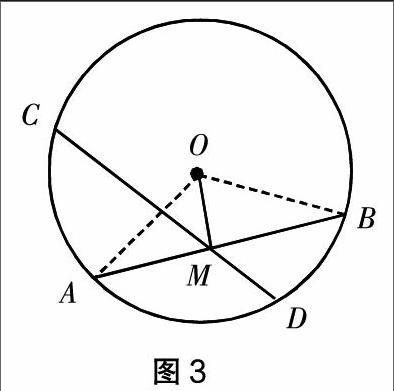
例如，有理數與無理數，分解與結合，形內與形外，直線與曲線等都是印象相反的事物. 在數學解題中，當直接證法難以奏效時，便會想到間接證法，當正面求解不易時，便聯想反面求答. 猶如我們幾何論證中經常涉及的反證法. 如幾何部分的“三角形中至少有一個內角不大于60°”“不在同一直線上的三點只能確定一個圓”等重要定理或推論的解釋，教師都離不開結論反面的聯想推理. 再看下面一例：如圖3，已知AB，CD是⊙O內非直徑的兩弦，求證：AB與CD不能互相平分.

顯然，本題從正面突破，很難處理. 因此教學時可啟發學生展開逆向思維，反向聯想. 證明如下：假設AB與CD能互相平分于點M，則由已知條件AB，CD均非⊙O直徑，可判定M不是圓心O，連接OA，OB，OM，由等腰三角形底邊上的中線垂直于底邊可得OM⊥AB，同理可得OM⊥CD，從而過點M有兩條直線AB，CD，都垂直于OM，這與過一點有且只有一條直線與已知直線垂直相矛盾. 故假設不成立，因此，AB與CD不能互相平分.

可見，運用反證法進行證題，能夠使學生通過反向聯想，加強學生認知結構上的全面性，避免學生思維過程及解題方法的單一、呆板性，從而更加促進學生創造思維的發展，進一步培養、提升思維的敏捷性. 由此，我們不難發現，積極引導學生逆向思維，反向聯想，不僅可以使解題方法簡明、明朗，還可以使學生在潛移默化中發展與提高學生的數學靈活思維的推理能力.

設計化歸聯想型問題，培養與提

高學生思維的邏輯性、獨立性

化歸聯想，即把問題從一個角度轉化到不同的角度，來讓學生把陌生的、待解決或未解決的問題通過某種轉化過程，歸結到一個已經能夠解決或容易解決的問題，從而求得原問題解答的一種手段和方法. 如在義務制九年級數學教科書中“圓”知識章節中圓周角定理的證明過程，教科書本身就巧妙布置了啟發學生作化歸聯想思維活動的不同圖形，再結合教師教學時的設計講解，啟發引導，不難達到將難點、重點簡化、易化，使學生耳目一新、思路清晰地釋疑解惑的目的. 可以說，化歸聯想使學生的思維不斷靈活、敏捷且富有邏輯性.

聯想是產生數學直覺思維的先導. 聯想思維更是解題成功的一半. 所以在教學中教師應精心設計一些聯想型問題引導學生有意識、有目的地進行聯想，更要善于讓學生選用最佳思路獨立地思考、思索、分析和解答問題，同時提倡不給予學生條條框框的限制，努力培養和發展學生的探索和創新精神，充分展示學生思維的靈活性、廣闊性、邏輯性等優良品質，從而進一步達到推進素質教育的目的.endprint