不識題目真面目,只“圓”深在此題中
蘇航赟
(江蘇省無錫市第三高級中學,江蘇 無錫 214028)
不識題目真面目,只“圓”深在此題中
蘇航赟
(江蘇省無錫市第三高級中學,江蘇 無錫 214028)
有關圓的問題是高考中的熱點,本文主要研究題目中隱含某動點的軌跡是圓的問題,如果我們沒有挖掘出這個圓,那么解題過程中會困難重重.然而我們一旦挖掘出這個圓,題目便會迎刃而解了.
隱含,軌跡,圓.
本文主要介紹題目中隱含某個動點的軌跡是圓,需要我們通過不同方法挖掘出來,撥開迷霧見真曉.
類型一動點到定點的距離為常數.



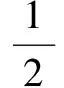
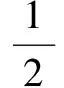

上述這一類型題中,主要是通過發現一動點到定點的距離為常數,從而得到動點的軌跡是圓,但有的題目從幾何關系中不容易發現某動點的軌跡是圓,而是需要通過代數運算得出動點的軌跡方程是圓方程,從而有助于解題.
類型二動點的軌跡方程為圓方程.
例2 已知B,C是圓O:x2+y2=4上的兩點,點A(1,1),且AB⊥AC,求線段BC的長的取值范圍.
探析本題求的是BC長的取值范圍,因為BC既是圓的弦又是Rt△ABC的斜邊,所以可以想到找BC中點H.由題可知AH=BH=CH,且OB2=OH2+BH2,這樣一來設出點H(x,y),就可以得到點H的軌跡方程是圓方程,從而進一步去解題.

解如圖,選取BC中點H,連接OH,AH,OB.
在Rt△ABC中,可知AH=BH=CH,
又在Rt△OBH中,可知OB2=OH2+BH2.
設點H(x,y),所以4=x2+
y2+x-12+y-12,


我們還接觸過一類特殊的圓——阿波羅尼斯圓,即一動點到兩定點的距離之比為常數(該常數不等于1),那么該動點的軌跡為圓.如果我們能熟練地運用該結論,有時會給我們的解題帶來方便.
類型三動點的軌跡為阿波羅尼斯圓.






由此看來,圓的美有時是隱藏著的,我們看不穿整個題目,不了解題目的真相,只是因為那個圓隱含在題目中,需要我們去挖掘,真是不識題目真面目,只“圓”深在此題中.
[1] 岳作仁.一類軌跡方程的復數求法[J].新疆教育學院學報, 1995(03).
[2] 周偉華.求動點的軌跡問題[J].重慶教育學院學報, 2007(03).
[責任編輯:楊惠民]
2017-07-01
蘇航赟(1985.10-),男,江蘇無錫人,研究生學歷,中學一級教師,主要從事高中數學教學研究.
G632
A
1008-0333(2017)28-0021-02

