基于辨識(shí)模型集的無(wú)人半潛水下機(jī)器人系統(tǒng)深度動(dòng)態(tài)滑模控制切換策略研究
周煥銀, 劉亞平, 胡志強(qiáng), 劉開(kāi)周, 衣瑞文
(1.東華理工大學(xué) 機(jī)械與電子工程學(xué)院, 江西 南昌 330013;2.中國(guó)科學(xué)院 沈陽(yáng)自動(dòng)化研究所 機(jī)器人學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 遼寧 沈陽(yáng) 110016)
基于辨識(shí)模型集的無(wú)人半潛水下機(jī)器人系統(tǒng)深度動(dòng)態(tài)滑模控制切換策略研究
周煥銀1,2, 劉亞平1, 胡志強(qiáng)2, 劉開(kāi)周2, 衣瑞文2
(1.東華理工大學(xué) 機(jī)械與電子工程學(xué)院, 江西 南昌 330013;2.中國(guó)科學(xué)院 沈陽(yáng)自動(dòng)化研究所 機(jī)器人學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 遼寧 沈陽(yáng) 110016)
BQ-01無(wú)人半潛水下機(jī)器人深度運(yùn)動(dòng)模型參數(shù)未知,無(wú)法為基于模型的控制策略提供控制參數(shù),導(dǎo)致該系統(tǒng)不易快速達(dá)到預(yù)期的性能指標(biāo)要求,為此提出一種多辨識(shí)模型動(dòng)態(tài)滑模控制方法。該控制方法采用平均擬合偏差方法,減少了系統(tǒng)辨識(shí)過(guò)程中出現(xiàn)過(guò)多冗余辨識(shí)模型參數(shù)組,以切換的方式為動(dòng)態(tài)滑模控制方法選取最佳模型參數(shù);同時(shí)采用狀態(tài)反饋方法實(shí)現(xiàn)滑模面抖動(dòng)指數(shù)衰減,從而解決了系統(tǒng)深度運(yùn)動(dòng)調(diào)節(jié)問(wèn)題。BQ-01系統(tǒng)湖泊試驗(yàn)結(jié)果表明,所提辨識(shí)方法能夠?yàn)榛?刂撇呗蕴峁┳罴芽刂茀?shù),且提高了系統(tǒng)運(yùn)動(dòng)控制品質(zhì)。
控制科學(xué)與技術(shù); 無(wú)人半潛水下機(jī)器人; 辨識(shí)模型; 動(dòng)態(tài)滑模控制; 控制品質(zhì)
0 引言
無(wú)人半潛水下機(jī)器人(USV)在海洋探測(cè)[1-3]或弱通信條件下與自治水下機(jī)器人通信等方面得到應(yīng)用[4-5]。本文所研究的USV系統(tǒng)BQ-01是一種可運(yùn)行于水下一定深度的近水面機(jī)器人,此系統(tǒng)下潛深度比較小,故所受外界環(huán)境干擾較大,且控制精度要求較高,這些都增加了系統(tǒng)控制算法設(shè)計(jì)的難度。針對(duì)USV系統(tǒng)所受外界干擾力問(wèn)題,文獻(xiàn)[6]在滑模控制的基礎(chǔ)上引入模糊邏輯概念解決了高頻抖動(dòng)對(duì)水下機(jī)器人系統(tǒng)近水面深度控制性能的影響,且仿真驗(yàn)證了算法的有效性;文獻(xiàn)[7]設(shè)計(jì)了一種帶有海浪濾波器的水下機(jī)器人深度控制方法解決系統(tǒng)在近水面航行過(guò)程中海浪波動(dòng)對(duì)系統(tǒng)深度控制效果的影響;文獻(xiàn)[8]提出增益降階輸出反饋法,并在自主水下機(jī)器人INFANTE AUV近水面深度控制中進(jìn)行了驗(yàn)證。滑模控制法對(duì)未知干擾項(xiàng)具有較強(qiáng)的魯棒性,在水下機(jī)器人系統(tǒng)中得到廣泛應(yīng)用[9-10]。
系統(tǒng)辨識(shí)是研究與建立系統(tǒng)模型的理論與方法。由于控制算法依賴于系統(tǒng)模型,對(duì)于模型參數(shù)未知的系統(tǒng),系統(tǒng)辨識(shí)為控制算法設(shè)計(jì)提供重要依據(jù)。許多專家[11-13]通過(guò)辨識(shí)實(shí)驗(yàn)獲取USV系統(tǒng)模型進(jìn)行控制算法的研究,文獻(xiàn)[14-15]采用聚類在線辨識(shí)以解決系統(tǒng)不確定性問(wèn)題,并通過(guò)了仿真實(shí)驗(yàn)驗(yàn)證算法。文獻(xiàn)[16]設(shè)計(jì)了一種基于遺傳算法的自抗擾控制器,此算法借助遺傳算法進(jìn)行控制。朱勝庭等[17]在最小二乘算法和遞推最小二乘算法基礎(chǔ)上提出了一種信息最小二乘算法用于對(duì)水下機(jī)器人Falcon動(dòng)力學(xué)模型辨識(shí)。由于系統(tǒng)辨識(shí)過(guò)程可近似為控制算法不斷學(xué)習(xí)認(rèn)識(shí)被控對(duì)象的過(guò)程,故消耗調(diào)節(jié)時(shí)間,影響系統(tǒng)動(dòng)態(tài)性能。
本文所研究的BQ-01系統(tǒng)是新研制的一類水下機(jī)器人系統(tǒng),其水動(dòng)力參數(shù)未知,針對(duì)所研究系統(tǒng)的垂直面水動(dòng)力參數(shù)未知的運(yùn)動(dòng)控制問(wèn)題,提出基于辨識(shí)模型集的動(dòng)態(tài)滑模控制法,通過(guò)辨識(shí)試驗(yàn)過(guò)程中所獲取的數(shù)據(jù)研究系統(tǒng)模型參數(shù)辨識(shí)。為了避免由于主觀原因造成模型辨識(shí)誤差過(guò)大的問(wèn)題,構(gòu)建了BQ-01系統(tǒng)過(guò)渡辨識(shí)模型集與臨時(shí)辨識(shí)模型集,根據(jù)臨時(shí)辨識(shí)模型集所獲取的模型參數(shù)構(gòu)建USV系統(tǒng)滑模控制參數(shù)集。為了從控制參數(shù)集中在線獲取最佳滑模控制參數(shù),本文提出基于事件驅(qū)動(dòng)的切換策略法,最后通過(guò)湖試對(duì)BQ-01的運(yùn)動(dòng)控制品質(zhì)進(jìn)行了驗(yàn)證分析。
1 USV系統(tǒng)深度控制模型
USV系統(tǒng)運(yùn)動(dòng)控制模型采用美國(guó)船舶運(yùn)動(dòng)控制界著名學(xué)者Fossen定義的水下機(jī)器人系統(tǒng)運(yùn)動(dòng)模型[18],USV系統(tǒng)的慣性坐標(biāo)系與載體坐標(biāo)系如圖1所示。深度控制模型結(jié)構(gòu)的一般表述形式為
(1)
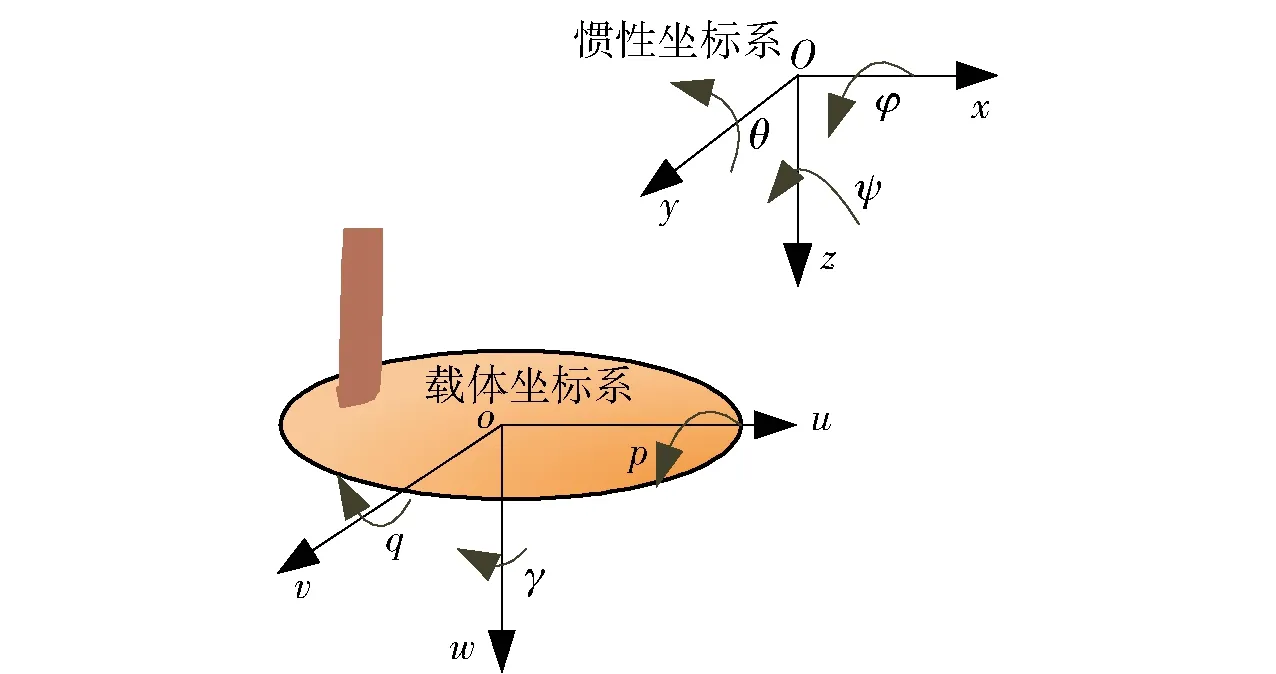
圖1 BQ-01系統(tǒng)坐標(biāo)系Fig.1 Coordinates of BQ-01 system
由于BQ-01系統(tǒng)的水動(dòng)力參數(shù)未知,故將深度控制模型(1)式轉(zhuǎn)化為
(2)
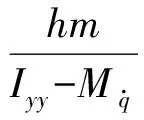
(3)
由于所研究的USV系統(tǒng)最大下潛深度為3.5 m,超過(guò)此閾值將會(huì)涉及USV系統(tǒng)安全問(wèn)題,故為了保護(hù)USV系統(tǒng),采用閉環(huán)模型辨識(shí)法對(duì)USV系統(tǒng)深度控制模型進(jìn)行辨識(shí)。
深度模型的參數(shù)估計(jì)采用基于PD控制的閉環(huán)辨識(shí)試驗(yàn),PD控制律δs,PD為
(4)
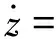
δs,PD=kPz+kDuθ,
(5)
將(5)式代入狀態(tài)方程(2)式:

(6)
(6)式所涉及的狀態(tài)量q、θ、u、z均可由相應(yīng)傳感器實(shí)時(shí)測(cè)量并反饋給控制器,且控制參數(shù)kP、kD已知。為了簡(jiǎn)化辨識(shí)模型,設(shè):
(7)
將方程組(7)式代入(6)式:
(8)
則待辨識(shí)模型結(jié)構(gòu)為
q(k+1)=a1θ(k)+a2Q(k)+bZ(k),
(9)
式中:a1、a2、b為USV系統(tǒng)深度控制模型待辨識(shí)參數(shù)。
2 USV系統(tǒng)深度控制模型集的參數(shù)估計(jì)
本文采用最小二乘辨識(shí)法對(duì)BQ-01系統(tǒng)深度控制模型參數(shù)進(jìn)行估計(jì)。
2.1基于平均擬合偏差的USV系統(tǒng)深度控制辨識(shí)模型集
根據(jù)最小二乘辨識(shí)法估計(jì)模型參數(shù)的基本步驟[20]對(duì)BQ-01模型參數(shù)進(jìn)行辨識(shí),待辨識(shí)模型結(jié)構(gòu)(9)式是單輸入多輸出(SIMO) 系統(tǒng),其中輸出量為[q(k+1),θ(k),Q(k)],輸入量為Z(k),將系統(tǒng)待辨識(shí)模型整理為
q(k+1)=a1θ(k)+a2Q(k)+bZ(k)+e(k),
(10)
式中:e(k)為實(shí)驗(yàn)?zāi)P推睢4孀R(shí)模型的最小二乘格式為
(11)
式中:?為待估計(jì)值。則系統(tǒng)辨識(shí)模型可進(jìn)一步描述為
q(k+1)=φT(k)?(k)+e(k).
(12)

(13)
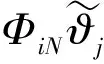
(14)
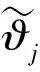
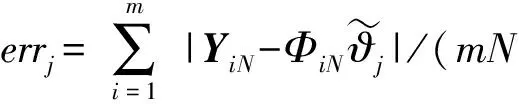
(15)
將獲取的平均擬和偏差errj記錄于對(duì)應(yīng)辨識(shí)模型中,用以判斷所獲得的模型參數(shù)是否滿足期望的平均擬和偏差的范圍。預(yù)設(shè)L組偏差范圍ξL,獲取系統(tǒng)過(guò)渡辨識(shí)模型參數(shù)。將滿足第k組擬合偏差范圍ξk要求的r組過(guò)渡辨識(shí)模型參數(shù)進(jìn)行平均擬合,獲取臨時(shí)辨識(shí)模型參數(shù):
(16)
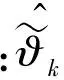
2.2USV深度辨識(shí)模型集構(gòu)建
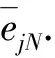

表1 深度控制過(guò)渡辨識(shí)模型集參數(shù)
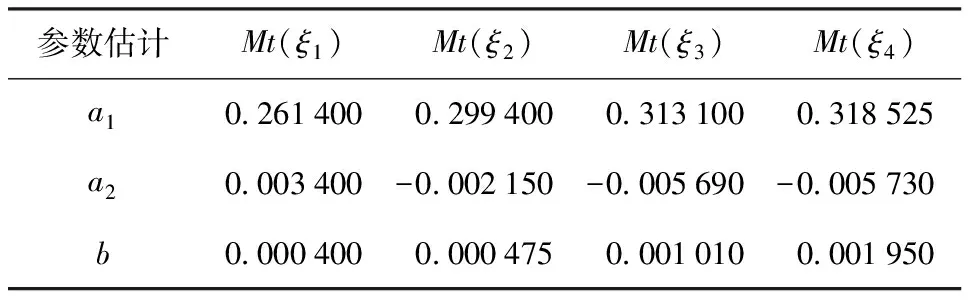
表2 深度控制臨時(shí)辨識(shí)模型集參數(shù)
對(duì)BQ-01系統(tǒng)深度控制模型中的縱傾角速度q的試驗(yàn)數(shù)據(jù)與仿真數(shù)據(jù)進(jìn)行曲線擬合,分析各辨識(shí)模型的精度。圖2、圖3為縱傾角速度q擬合曲線,其中虛線為BQ-01系統(tǒng)實(shí)際運(yùn)行曲線,實(shí)線為辨識(shí)后模型輸出曲線。圖2的平均擬合偏差ξ≈1.8遠(yuǎn)小于構(gòu)建此臨時(shí)模型的所有過(guò)渡辨識(shí)模型的擬合偏差范圍3<ξ2<4;圖3的平均擬合偏差ξ≈0.42小于ξ3所包含的范圍。通過(guò)對(duì)圖2與圖3的分析表明:臨時(shí)辨識(shí)模型輸出值與試驗(yàn)輸出平均擬合間的偏差遠(yuǎn)小于所設(shè)的平均擬合偏差,臨時(shí)辨識(shí)模型的辨識(shí)精度比過(guò)渡辨識(shí)模型的辨識(shí)精度高。
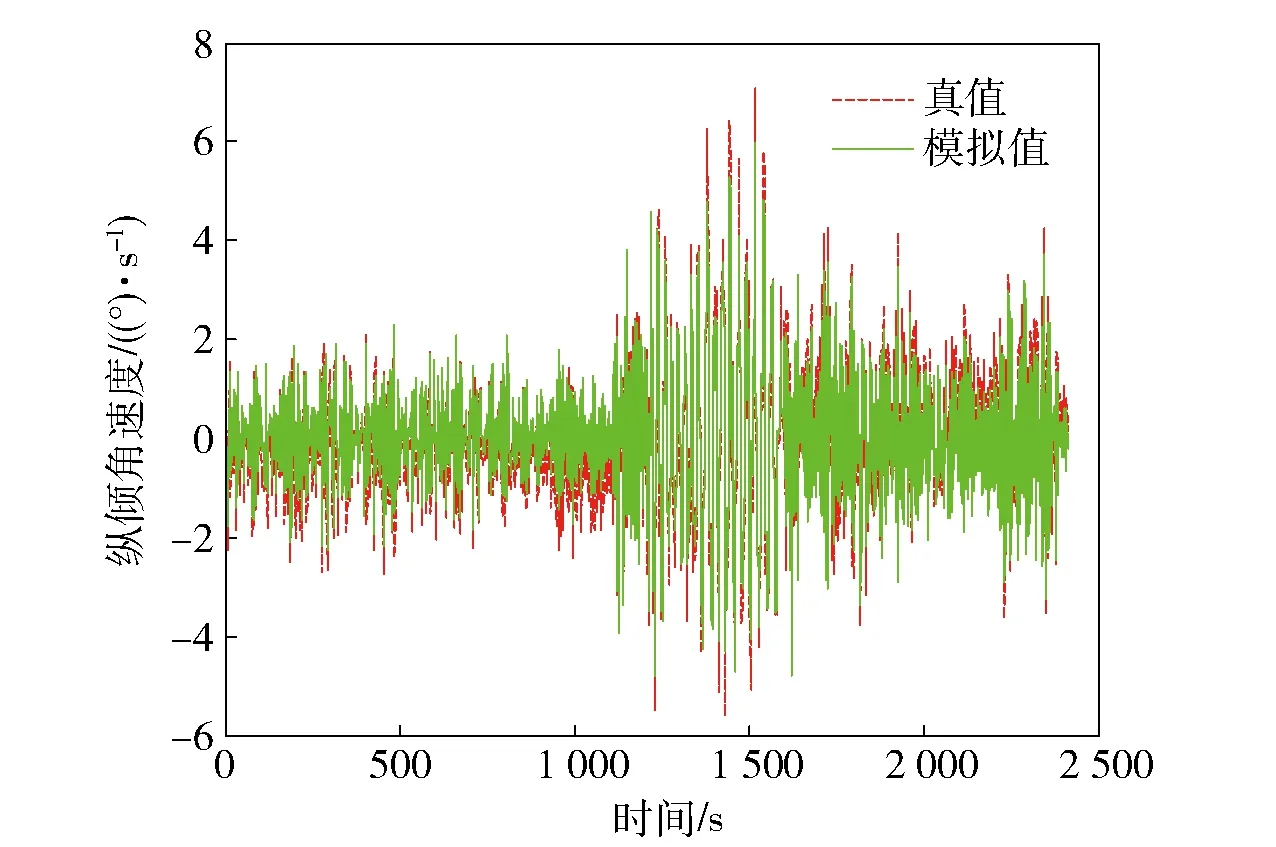
圖2 平均擬合偏差范圍為ξ2的q擬合曲線圖Fig.2 Fitting curves of q in the fitting error range ξ2
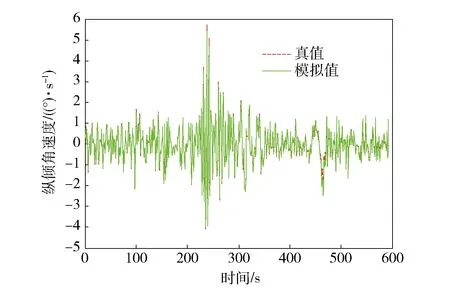
圖3 平均擬合偏差范圍為ξ3的q擬合曲線Fig.3 Fitted curves of q in the fitting error range ξ3
3 USV動(dòng)態(tài)滑模控制方法與切換策略構(gòu)建
BQ-01是一種采用柴油機(jī)為動(dòng)力源,艇體主體潛于水下、僅通氣桅桿穿透水面的新型水下機(jī)器人系統(tǒng)。BQ-01是國(guó)內(nèi)率先實(shí)現(xiàn)此類功能的USV系統(tǒng)。系統(tǒng)性能指標(biāo)為最大航速為10 kn,水平舵最大轉(zhuǎn)動(dòng)角度為25°,最大下潛深度為3.5 m,系統(tǒng)采樣時(shí)間為0.5 s. 系統(tǒng)的深度控制執(zhí)行機(jī)構(gòu)為布置在USV艏艉部?jī)蓚?cè)的水平舵,通過(guò)兩組水平舵上下轉(zhuǎn)動(dòng)所產(chǎn)生的縱傾角實(shí)現(xiàn)USV系統(tǒng)下潛或上浮。湖泊試驗(yàn)過(guò)程中,“BQ-01”水動(dòng)力參數(shù)未知。
BQ-01系統(tǒng)的動(dòng)力推進(jìn)及操縱系統(tǒng)設(shè)計(jì)方案如圖4所示。其中:動(dòng)力推進(jìn)系統(tǒng)由柴油機(jī)通過(guò)齒輪箱帶動(dòng)噴水推進(jìn)器,實(shí)現(xiàn)USV的航行驅(qū)動(dòng);操縱系統(tǒng)主要由艏艉各兩片水平舵組成,舵機(jī)為液壓驅(qū)動(dòng),實(shí)現(xiàn)垂直面定深等航行控制;而水平面定向等航行控制通過(guò)噴水推進(jìn)器的噴口左右偏轉(zhuǎn)產(chǎn)生的矢量推力實(shí)現(xiàn);柴油機(jī)通過(guò)桅桿頂部的浮閥實(shí)現(xiàn)進(jìn)排氣,由水平舵控制USV的航行吃水深度,避免水通過(guò)進(jìn)排氣口倒灌進(jìn)內(nèi)部危及USV安全。
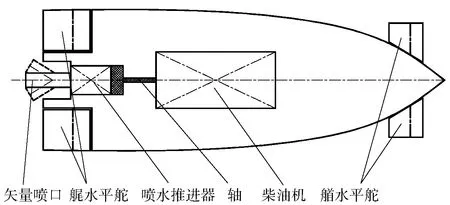
圖4 BQ-01動(dòng)力推進(jìn)及操縱系統(tǒng)Fig.4 Propulsion and control system
由于在湖泊試驗(yàn)過(guò)程中,BQ-01水動(dòng)力參數(shù)未知,本文以臨時(shí)辨識(shí)模型集中各模型參數(shù)為依據(jù)構(gòu)建多組滑模控制參數(shù),根據(jù)USV系統(tǒng)運(yùn)動(dòng)控制特點(diǎn),通過(guò)預(yù)設(shè)切換策略實(shí)現(xiàn)最佳控制策略的選取。圖5為BQ-01系統(tǒng)準(zhǔn)備試驗(yàn)圖。

圖5 BQ-01系統(tǒng)Fig.5 BQ-01 system
3.1基于多辨識(shí)模型切換的USV動(dòng)態(tài)狀態(tài)滑模控制參數(shù)集構(gòu)建
為了避免縱向速度u的深度控制強(qiáng)耦合性,本文提出了動(dòng)態(tài)滑模控制法。為了避免縱向速度對(duì)深度控制的影響,滑模控制參數(shù)可根據(jù)縱向速度進(jìn)行動(dòng)態(tài)調(diào)整,此方法避免了傳統(tǒng)外場(chǎng)試驗(yàn)中的分段調(diào)整弊端,如不同速度段需設(shè)置不同的控制參數(shù)等,從而縮短了外場(chǎng)試驗(yàn)次數(shù)。
另外,由于USV系統(tǒng)深度控制參數(shù)是通過(guò)辨識(shí)模型集提供的,系統(tǒng)滑模控制參數(shù)將有多組,為了獲取最佳控制策略,故本文提出了基于事件驅(qū)動(dòng)的多辨識(shí)模型切換策略法。
為了避免USV系統(tǒng)縱傾角過(guò)大導(dǎo)致系統(tǒng)迅速下潛,超出下潛深度閾值,本文采用雙環(huán)控制即深度ez=z-zd與縱傾角eθ=θ-θd同時(shí)閉環(huán)控制,其中深度期望值z(mì)d、縱傾角的期望值θd均為0,則深度誤差控制狀態(tài)方程可表述為
(17)
式中:δs為水平舵輸出的舵角(rad)。
設(shè)系統(tǒng)滑模面為
S=q-(c1ez+c2eθ),
(18)
式中:c1與c2為預(yù)設(shè)的滑模控制參數(shù)。
由于滑模面的抖動(dòng)是滑模控制設(shè)計(jì)過(guò)程中的一大難點(diǎn),為了削弱滑模面抖動(dòng),提出基于狀態(tài)反饋的滑模控制,具體構(gòu)建過(guò)程如下:

(19)
2) 根據(jù)狀態(tài)反饋控制法[21]配置模型(19)式的期望閉環(huán)極點(diǎn)為λz<0與λθ<0,獲取狀態(tài)反饋控制律為
=(λz+λθ)θ+z.
(20)
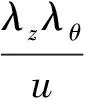
S=q-≈eq.
(21)
3) 對(duì)滑模面S求導(dǎo)
(22)

(23)
4) 令
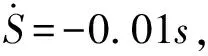
(24)
以保證滑模控制器指數(shù)衰減,將(21)式代入(24)式,有
(25)
5) 由(23)式與(25)式獲取基于狀態(tài)反饋的滑模控制律為
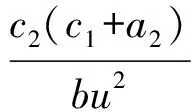
(26)
以上公式的詳細(xì)推導(dǎo)過(guò)程詳見(jiàn)文獻(xiàn)[21]。為了避免縱向速度過(guò)小導(dǎo)致控制參數(shù)過(guò)大,預(yù)設(shè)縱向速度在控制律(26)式中的約束條件為
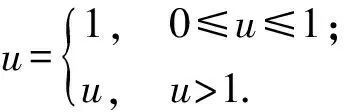
(27)
6) 將狀態(tài)反饋配置的期望閉環(huán)極點(diǎn)λz與λθ代入c1與c1,將表2參數(shù)分別代入控制律(26)式,獲取多組動(dòng)態(tài)變化的滑模控制參數(shù),組成滑模控制器參數(shù)集。
為了從控制參數(shù)集中獲取最佳控制參數(shù),本文設(shè)計(jì)了基于事件驅(qū)動(dòng)的切換策略。
3.2基于BQ-01系統(tǒng)深度控制性能的切換策略設(shè)計(jì)
為了保證BQ-01系統(tǒng)湖試過(guò)程中,不會(huì)由于滑模控制參數(shù)選取不恰當(dāng)而導(dǎo)致的系統(tǒng)安全性問(wèn)題,本文采用兩類基于事件驅(qū)動(dòng)的切換策略:緊急切換策略與穩(wěn)定切換策略。
為了確保設(shè)備安全,試驗(yàn)過(guò)程中,設(shè)計(jì)了兩套性能指標(biāo)要求:1)最佳控制策略選取過(guò)程中的性能指標(biāo);2)期望性能指標(biāo)。其中,最佳控制策略選取過(guò)程中的性能指標(biāo)為:最大下潛深度不超過(guò)3.2 m,超調(diào)量δp≤50%,最大振幅不超過(guò)0.5 m,靜態(tài)誤差es≤20%,調(diào)節(jié)時(shí)間ts≤300 s. 期望性能指標(biāo)要求:最大下潛深度不超過(guò)3.2 m,超調(diào)量δp=10%,靜態(tài)誤差es≤3%,調(diào)節(jié)時(shí)間ts≤120 s,無(wú)震蕩。
3.2.1 切換策略的設(shè)置
緊急切換策略的設(shè)置:根據(jù)USV系統(tǒng)控制要求與系統(tǒng)安全,其最大下潛深度為3.5 m,故在BQ-01系統(tǒng)深度控制過(guò)程中設(shè)計(jì)了基于深度閾值z(mì)>3.2 m的緊急切換策略,超出此閾值系統(tǒng)停止執(zhí)行所有使命要求,直至浮出水面,接收下一條深度控制使命;與基于超調(diào)量δp≥50%的緊急切換策略,超出此閾值BQ-01系統(tǒng)停車,浮出水面后,切換到下一組控制參數(shù)運(yùn)行,以避免系統(tǒng)運(yùn)動(dòng)出現(xiàn)不穩(wěn)定現(xiàn)象。
穩(wěn)定切換策略主要用于在線選取滿足USV系統(tǒng)預(yù)設(shè)控制要求的控制參數(shù),如果系統(tǒng)在預(yù)設(shè)時(shí)間(500 s)內(nèi)未出現(xiàn)超調(diào)過(guò)大問(wèn)題,則認(rèn)為此組控制參數(shù)穩(wěn)定,BQ-01系統(tǒng)將把相關(guān)控制參數(shù)保留下來(lái);否則,將切換到下一組控制參數(shù)下進(jìn)行驗(yàn)證。預(yù)設(shè)時(shí)間是由有經(jīng)驗(yàn)的海洋機(jī)器人控制專家設(shè)定,此段時(shí)間能夠判斷BQ-01系統(tǒng)是否達(dá)到期望的控制品質(zhì)要求。
穩(wěn)定切換過(guò)程中最佳控制策略的選取。依據(jù)各臨時(shí)辨識(shí)模型而設(shè)計(jì)的滑模控制參數(shù),其取舍決定于系統(tǒng)辨識(shí)模型與實(shí)際系統(tǒng)模型的擬合程度。若多個(gè)控制策略同時(shí)滿足預(yù)期控制性能指標(biāo)要求,則BQ-01系統(tǒng)選取控制品質(zhì)最高的控制策略作為當(dāng)前運(yùn)行環(huán)境下的最佳控制策略。若某控制策略在不同運(yùn)行環(huán)境下均保持良好的控制品質(zhì)或達(dá)到預(yù)期的控制性能指標(biāo)要求,則認(rèn)為此辨識(shí)模型參數(shù)逼近于實(shí)際系統(tǒng)模型參數(shù),稱此參數(shù)對(duì)應(yīng)的控制策略為最佳控制策略。
3.2.2 控制參數(shù)集的在線選取原則
根據(jù)BQ-01系統(tǒng)臨時(shí)辨識(shí)模型集而設(shè)計(jì)的一系列控制策略組成控制參數(shù)集,故需根據(jù)系統(tǒng)運(yùn)動(dòng)控制品質(zhì)與切換策略從控制參數(shù)集中選取一組最佳參數(shù)作為系統(tǒng)控制策略參數(shù)。
切換前后系統(tǒng)穩(wěn)定性分析。根據(jù)穩(wěn)定切換定理——公共李雅普諾夫法可知:在系統(tǒng)運(yùn)行過(guò)程中,兩控制策略切換前后,系統(tǒng)保持穩(wěn)定,則切換前后所對(duì)應(yīng)的控制策略均可保證系統(tǒng)穩(wěn)定;若系統(tǒng)切換前不穩(wěn)定,切換后系統(tǒng)穩(wěn)定,則切換后控制策略對(duì)應(yīng)的辨識(shí)模型與實(shí)際系統(tǒng)模型擬合;若切換前穩(wěn)定,切換后系統(tǒng)不穩(wěn)定,則切換前對(duì)應(yīng)控制策略可保證系統(tǒng)穩(wěn)定,但無(wú)法判斷切換后的控制策略能否保證系統(tǒng)的穩(wěn)定性。
從滑模控制策略律(22)式可知,若系統(tǒng)辨識(shí)模型可表述系統(tǒng)深度控制模型,那么系統(tǒng)深度控制應(yīng)為全局漸近穩(wěn)定,若系統(tǒng)運(yùn)行過(guò)程不穩(wěn)定,則可認(rèn)為系統(tǒng)辨識(shí)模型與實(shí)際模型不匹配。對(duì)于切換前穩(wěn)定的控制策略,切換后系統(tǒng)不穩(wěn)定,有可能是由于切換前控制策略在切換點(diǎn)附近引起控制執(zhí)行機(jī)構(gòu)的共振。而切換后系統(tǒng)穩(wěn)定,則需通過(guò)試驗(yàn)驗(yàn)證后,判斷此組控制參數(shù)能否保證系統(tǒng)穩(wěn)定。
將臨時(shí)辨識(shí)模型集中的模型參數(shù)代入(22)式中構(gòu)建控制參數(shù)集,預(yù)設(shè)緊急切換策略、穩(wěn)定切換策略作為事件驅(qū)動(dòng)條件,從控制參數(shù)集中選取USV系統(tǒng)最佳控制策略參數(shù)。選取最佳控制策略參數(shù)原則如下:
1) 緊急切換。若系統(tǒng)深度控制過(guò)程中出現(xiàn)不穩(wěn)定現(xiàn)象,或超調(diào)量達(dá)到δp≥50%條件,或系統(tǒng)深度超出3.2 m,則啟動(dòng)緊急切換策略,系統(tǒng)停止運(yùn)行,上浮后,切換到下一組控制策略。
2) 穩(wěn)定切換。若系統(tǒng)在預(yù)設(shè)時(shí)間t>500 s內(nèi)保持穩(wěn)定,則記錄此組控制參數(shù)后,切換到下一組控制策略。
3) 穩(wěn)定切換采用順序切換法,從控制參數(shù)集中依次選取各控制策略,依據(jù)切換系統(tǒng)的穩(wěn)定判據(jù)公共李雅普諾夫法,以及系統(tǒng)在各控制策略控制下所表現(xiàn)的控制品質(zhì),記錄滿足預(yù)期性能指標(biāo)要求的控制策略序號(hào)與控制參數(shù)。
4) 若系統(tǒng)在某控制策略控制下穩(wěn)定且動(dòng)態(tài)性能較好,則改變USV系統(tǒng)使命,要求檢驗(yàn)該控制策略在不同運(yùn)動(dòng)要求下的控制品質(zhì)。如果系統(tǒng)達(dá)到預(yù)期的控制性能指標(biāo)要求,則控制參數(shù)集將此控制策略作為最佳控制參數(shù)。
5) 繼續(xù)在臨時(shí)辨識(shí)模型集中切換,直至所有控制參數(shù)驗(yàn)證完畢。
根據(jù)BQ-01系統(tǒng)所記錄序號(hào)和控制參數(shù),分析最佳控制策略所對(duì)應(yīng)的深度運(yùn)行曲線,研究系統(tǒng)動(dòng)態(tài)性能出現(xiàn)的問(wèn)題,進(jìn)一步改善系統(tǒng)控制策略參數(shù)。
3.3USV系統(tǒng)湖試試驗(yàn)數(shù)據(jù)分析
將臨時(shí)辨識(shí)模型集中的各模型參數(shù)代入滑模控制律(22)式,構(gòu)建控制參數(shù)集,并將其嵌入BQ-01系統(tǒng)深度控制模塊,預(yù)設(shè)各控制策略順序、預(yù)期性能指標(biāo)要求、切換策略以及待記錄信息等,通過(guò)USV系統(tǒng)湖試在線選取期望的控制策略。BQ-01所采用的深度計(jì)量程0~30 m,非線性誤差±0.2%,長(zhǎng)期穩(wěn)定性±0.1%.
圖6為在線選取控制策略試驗(yàn)數(shù)據(jù)分析曲線圖,期望深度為1.6 m,時(shí)間軸出現(xiàn)的間隔,則是系統(tǒng)根據(jù)使命執(zhí)行過(guò)程中出現(xiàn)危險(xiǎn)狀況、下潛深度超出閾值或使命要求而浮出水面的過(guò)程。從圖6數(shù)據(jù)輸出曲線可知,深度控制參數(shù)集所含各控制策略都無(wú)法達(dá)到預(yù)期控制性能指標(biāo)要求,深度控制輸出曲線產(chǎn)生振幅為0.5~1.0 m的震蕩。有關(guān)切換策略的啟動(dòng)記錄已在圖6中標(biāo)注,BQ-01系統(tǒng)將振幅最小的一組模型作為最佳控制策略,并進(jìn)行保存。完成辨識(shí)試驗(yàn)后,以系統(tǒng)控制參數(shù)集所選取的最佳控制參數(shù)為基準(zhǔn)進(jìn)行離線調(diào)整。圖7為BQ-01系統(tǒng)控制參數(shù)逐漸改進(jìn)后的曲線對(duì)比圖。圖7(a)為控制參數(shù)未調(diào)整前BQ-01系統(tǒng)深度控制運(yùn)行曲線圖。從圖7(a)中可以看出深度有較大曲線震蕩,雖然此振幅滿足試驗(yàn)初期所設(shè)要求,但并非期望現(xiàn)象。為了減少震蕩,將滑模面進(jìn)行調(diào)整并將辨識(shí)模型參數(shù)a2下調(diào),USV系統(tǒng)深度控制輸出曲線如圖7(b)所示。試驗(yàn)數(shù)據(jù)分析表明,系統(tǒng)深度控制的動(dòng)態(tài)性能得到很大改善,但系統(tǒng)深度控制存在較大靜態(tài)誤差與調(diào)節(jié)時(shí)間長(zhǎng)等控制品質(zhì)問(wèn)題。為了減少靜態(tài)誤差,根據(jù)PID控制中積分控制參數(shù)的作用,加入積分項(xiàng),系統(tǒng)輸出曲線如圖7(c)所示。試驗(yàn)數(shù)據(jù)分析表明,系統(tǒng)深度控制調(diào)節(jié)時(shí)間變短(ts=75 s),且達(dá)到預(yù)期靜態(tài)誤差小于3%要求,超調(diào)變小,無(wú)抖動(dòng)。
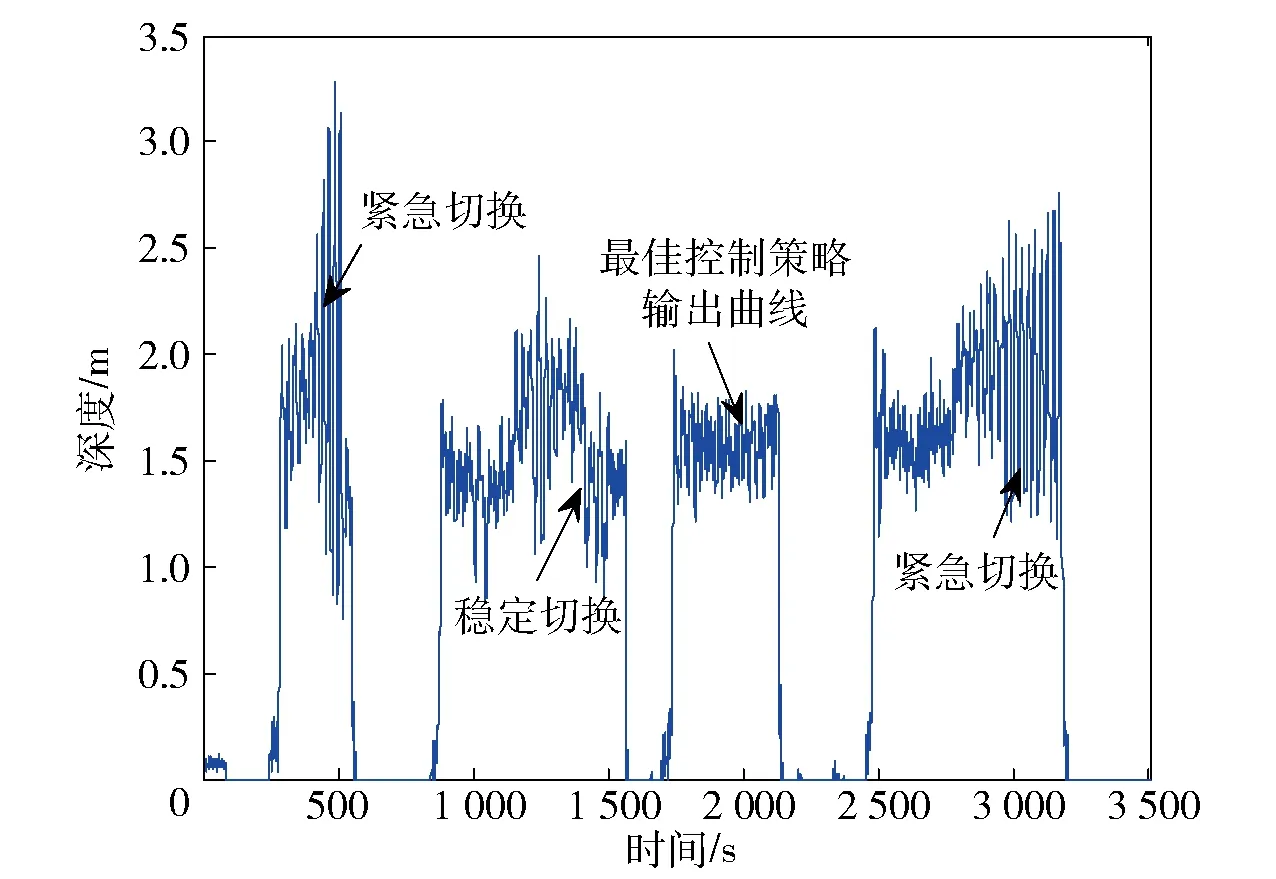
圖6 控制參數(shù)集在線選取最佳控制策略參數(shù)過(guò)程輸出曲線Fig.6 Output curves of on-line selected best controller processes in controller set
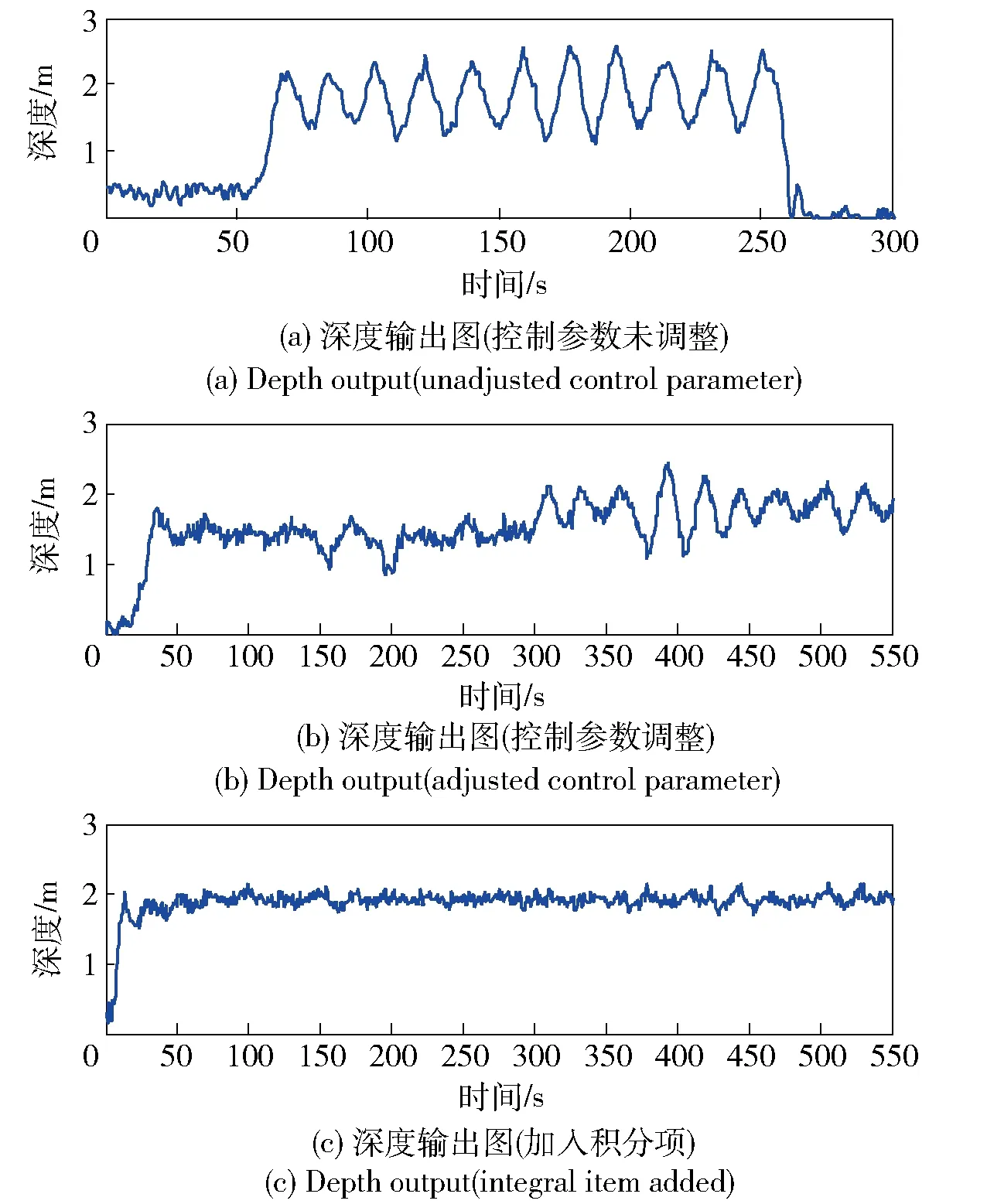
圖7 USV系統(tǒng)控制參數(shù)調(diào)整前后深度控制曲線對(duì)比圖Fig.7 Depth control curves before and after parameter adjustment
圖8為BQ-01系統(tǒng)定深1 m時(shí),系統(tǒng)深度控制運(yùn)行曲線。其中:圖8(a)為滑模面控制參數(shù)改進(jìn)后的BQ-01輸出曲線,其具有較大靜態(tài)誤差,為0.7 m;圖8(b)是BQ-01系統(tǒng)滑模控制部分加入積分項(xiàng)后系統(tǒng)深度控制運(yùn)行曲線,BQ-01系統(tǒng)靜態(tài)誤差減小,提高了BQ-01系統(tǒng)的控制品質(zhì)。

圖8 最佳控制模型參數(shù)改善前后深度控制曲線Fig.8 Depth control urves of improved and unimproved best suitable depth control parameters
圖9為BQ-01定深3 m的控制曲線圖。系統(tǒng)定深3 m時(shí),為了避免由于縱傾角過(guò)大或慣性大等原因?qū)е翨Q-01系統(tǒng)下潛深度超出閾值,需預(yù)設(shè)下潛2 m左右后再下潛3 m. 從圖9中可以看出,BQ-01定深3 m時(shí)具有良好的控制品質(zhì),數(shù)據(jù)分析表明靜態(tài)誤差小于3%,達(dá)到預(yù)期控制性能指標(biāo)要求。
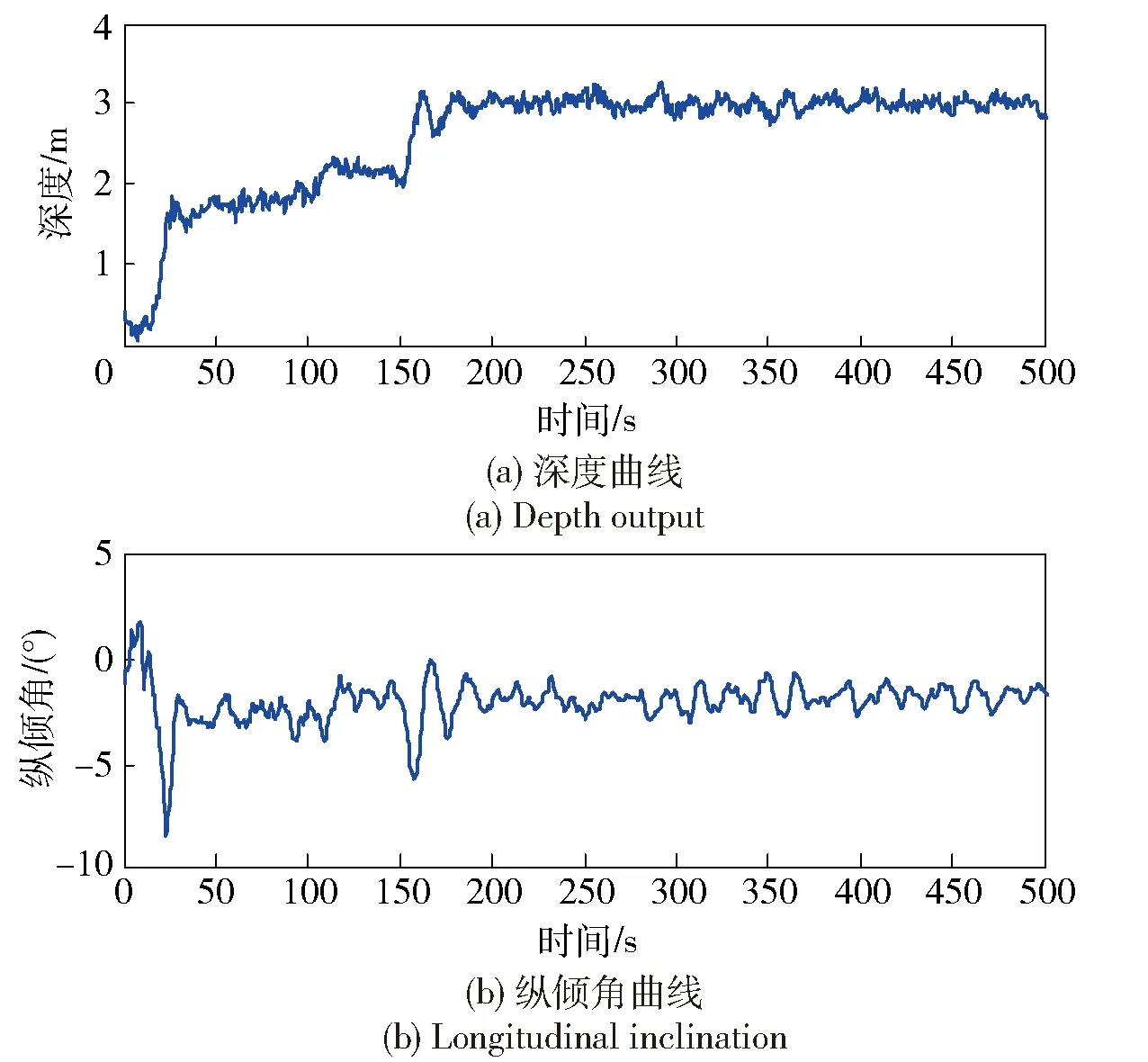
圖9 最佳控制模型參數(shù)改善后下潛3 m深度控制曲線Fig.9 3 m depth control curves of improved best suitable depth control parameters
湖試數(shù)據(jù)分析表明,本文所提控制策略設(shè)計(jì)方案提高了BQ-01系統(tǒng)運(yùn)動(dòng)控制品質(zhì),基于深度辨識(shí)模型集的滑模控制法可實(shí)現(xiàn)系統(tǒng)在不同使命要求下保持良好的控制品質(zhì)。
4 結(jié)論
本文針對(duì)所研究USV系統(tǒng)深度控制模型參數(shù)未知問(wèn)題,提出了基于深度辨識(shí)模型集的動(dòng)態(tài)滑模控制法,并構(gòu)建了動(dòng)態(tài)狀態(tài)滑模控制參數(shù)集。根據(jù)所研究USV系統(tǒng)BQ-01提出基于緊急切換與穩(wěn)定切換的切換策略,從控制參數(shù)集中篩選出最佳控制策略,最后根據(jù)BQ-01系統(tǒng)運(yùn)動(dòng)控制性能,對(duì)控制參數(shù)進(jìn)一步完善。通過(guò)湖試表明本文所提控制策略設(shè)計(jì)方案達(dá)到了預(yù)期的控制性能指標(biāo)要求:調(diào)節(jié)時(shí)間變短,靜態(tài)誤差達(dá)到小于3%,無(wú)震蕩等。所提基于辨識(shí)模型集的滑模控制方法簡(jiǎn)化了控制策略設(shè)計(jì)過(guò)程,節(jié)約了試驗(yàn)時(shí)間。
References)
[1] Garus J, Szymak P. Semiautomatic Control of self-propelled mine counter charge in plane motion[C]∥ Proceedings of the 8th WSEAS International Conference on Electric Power Systems, High Voltages, Electric Machines. Venice, Italy:World Scientific and Engineering Academy and Society , 2008: 217-221.
[2] Hunter R S, Brown C, Jenkins L K, et al. Bathy boat: an autonomous surface vessel for stand-alone survey and underwater vehicle network supervision[J]. Marine Technology Society Journal, 2010, 44(4):20-29.
[3] Liu Y F, Noguchi N. Development of an unmanned surface vehicle for autonomous navigation in a paddy field[J]. Engineering in Agriculture, Environment and Food, 2016, 9(1):21-26.
[4] Alleman P, Kleiner A, Steed C, et al. Development of a new unmanned semi-submersible (USS) vehicle[C]∥ Proceedings of Oceans 2009 Conference. Biloxi, MS, US:IEEE,2009 : 2416-2421.
[5] 冀大雄, 任申真,胡志強(qiáng). 弱通信條件下USV對(duì)AUV的自主跟蹤控制研究[J]. 科學(xué)通報(bào), 2013, 58(增刊) :49-54.
JI Da-xiong, REN Shen-zhen,HU Zhi-qiang. Autonomous tracking unmanned underwater vehicle using unmanned surface vehicle under the condition of weak communication[J]. Science China Press, 2013, 58(S): 49-54. (in Chinese)
[6] 沈建森, 周徐昌,高璇. 遠(yuǎn)程AUV近水面運(yùn)動(dòng)縱向模糊滑模控制[J]. 魚雷技術(shù), 2011, 19(5): 360-364.
SHEN Jian-sen, ZHOU Xu-chang, GAO Xuan. Fuzzy sliding mode control for near-surface AUV in longitudinal plane[J].Torpedo Techenology, 2011, 19(5): 360-364. (in Chinese)
[7] 嚴(yán)浙平, 李聰聰, 張宏瀚,等. 基于海浪干擾濾波器的UUV近水面深度控制[J]. 船舶工程, 2013, 35(4): 71-74.
YAN Zhe-ping, LI Cong-cong, ZHANG Hong-han,et al. Depth control for UUVs manoeuvring near-surface based on wave disturbance filter[J]. Ship Engineering, 2013, 35(4): 71-74.(in Chinese)
[8] Silvestre C, Pascoal A. Depth control of the INFANTE AUV using gain-scheduled reduced order output feedback [J]. Control Engineering Practice, 2007, 15(7):883-895.
[9] 魏延輝, 周衛(wèi)祥, 陳巍, 等. 基于NDO的ROV變深自適應(yīng)終端滑模控制器設(shè)計(jì)[J]. 控制與決策, 2016, 31(2): 373-377.
WEI Yan-hui, ZHOU Wei-xiang, CHEN Wei,et al. Design of adaptive terminal sliding mode controller based on nonlinear disturbance observer for ROV depth changing[J]. Control and Decision, 2016, 31(2): 373-377. (in Chinese)
[10] Zhou H Y, Liu K Z, Li Y P ,et al. Dynamic sliding mode control based on multiple for the depth control of autonomous underwater vehicles[J]. International Journal of Advanced Robotic Systems, 2015, 12(7):1-10.
[11] 白偉偉,任俊生,李鐵山,等. 基于局部最優(yōu)LWL的船舶操縱運(yùn)動(dòng)辨識(shí)建模[J]. 哈爾濱工程大學(xué)學(xué)報(bào), 2017, 38(5): 676-683.
BAI Wei-wei,REN Jun-sheng, LI Tie-shan, et al.Locally optimal-based LWL identification modeling for ship manoeuvring motion[J]. Journal of Harbin Engineering University, 2017,38(5):676-683. (in Chinese)
[12] Sonnenburg C R, Woolsey C A. Modeling, identification, and control of an unmanned surface vehicle[J]. Journal of Field Robotics, 2013, 30(3):371-398.
[13] 董早鵬, 萬(wàn)磊, 孫玉山, 等. 基于非對(duì)稱模型的欠驅(qū)動(dòng)無(wú)人海洋運(yùn)載器軌跡跟蹤控制[J]. 兵工學(xué)報(bào), 2016, 37(3): 471-481.
DONG Zao-peng, WAN Lei, SUN Yu-shan, et al.Trajectory tracking control of an underactuated unmanned marine vehicle based on asymmetric model[J].Acta Armamentarii, 2016, 37(3): 471-481.(in Chinese)
[14] 梁輝, 童朝南. 基于減法聚類的帶鋼厚度數(shù)據(jù)驅(qū)動(dòng)建模[J]. 北京科技大學(xué)學(xué)報(bào), 2012, 34(11):1338-1345.
LIANG Hui, TONG Chao-nan. Online data-driven modeling for strip thickness based on subtractive clustering[J]. Journal of University of Science and Technology Beijing, 2012, 34(11):1338-1345. (in Chinese)
[15] 段朝陽(yáng),張艷,邵雷登,等. 基于多模型在線辨識(shí)的滑模變結(jié)構(gòu)控制[J]. 上海交通大學(xué)學(xué)報(bào), 2011, 45(3):403-407.
DUAN Chao-yang, ZHANG Yan, SHAO Lei-deng, et al. Sliding mode variable structure control based on multi-model on-line identification [J]. Journal of Shanghai Jiao Tong University, 2011, 45(3): 403-407.(in Chinese)
[16] 胡坤, 張孝芳, 劉常波. 基于遺傳算法的無(wú)人水下航行器深度自抗擾控制[J]. 兵工學(xué)報(bào), 2013, 34(2):217-222.
HU Kun, ZHANG Xiao-fang, LIU Chang-bo.Unmanned underwater vehicle depth ADRC based on genetic algorithm near surface[J]. Acta Armamentarii, 2013, 34(2):217-222. (in Chinese)
[17] 朱勝庭,朱大奇,鄧志剛. 多信息最小二乘法辨識(shí)水下機(jī)器人動(dòng)力學(xué)模型[J]. 系統(tǒng)仿真學(xué)報(bào),2013,25(6):1399-1404.
ZHU Sheng-ting, ZHU Da-qi,DENG Zhi-gang. Identification of underwater vehicle dynamic model using multi-innovation least square algorithm[J]. Journal of System Simulation, 2013,25(6):1399-1404.(in Chinese)
[18] Fossen T I. Guidance and control of ocean vehicles[M]. New York, NY, US:John Willey & Sons Ltd, 1994:21-56.
[19] 蔣新松,封錫盛,王棣堂. 水下機(jī)器人[M].沈陽(yáng):遼寧科學(xué)技術(shù)出版社, 2000.
JIANG Xin-song, FENG Xi-sheng, WANG Di-tang. Underwater vehicles[M]. Shenyang: Liaoning Science and Technology Press,2000. (in Chinese)
[20] 丁峰. 系統(tǒng)辨識(shí)新論[M]. 北京:科學(xué)出版社, 2013.
DING Feng. New theories of system identification[M].Beijing: Science Press, 2013. (in Chinese)
[21] Zhou H Y, Liu K Z, Feng X S. State feedback sliding mode control without chattering by constructing Hurwitz matrix for AUV movement[J]. International Journal of Automation and Computing, 2011, 8(2): 262-268.
SwitchingStrategyofDynamicSlidingModeControlBasedonMultipleIdentificationModelSetforUnmannedSemi-submersibleVehicle
ZHOU Huan-yin1,2, LIU Ya-ping1, HU Zhi-qiang2, LIU Kai-zhou2, YI Rui-wen2
(1.School of Mechanical and Electrical Engineering, East China University of Technology, Nanchang 330013, Jiangxi, China; 2.State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, Liaoning, China)
The control parameters can not be provided for the model-based control algorithm, which leads to the undesirable control performances of the system since the depth motion model parameters regarding the unmanned semi-submersible vehicles (USVs ) BQ-01 are unknown. For this purpose, a multi-identification model-based dynamic sliding mode control algorithm is presented for the investigation of system’s control problem on the desired depth. In the proposed algorithm, the average-fitting-error method is used to reduce the excessive redundant model parameters, and thus the optimum model parameters is provided for the control algorithm by switching methods. And the state feedback method is used to bring about the chattering exponential decay of sliding mode controller so as to reduce the settling time. The experimental results of lake trials demonstrates that the proposed algorithm could offer the best model parameters for sliding mode control, and the dynamic sliding mode control with multi-identification models is capable of ensuring BQ-01 system to achieve the ideal control performance.
control science and technology; unmanned semi-submersible vehicle; multiple identification model; dynamic sliding mode control; control performance
TP273
A
1000-1093(2017)11-2198-09
10.3969/j.issn.1000-1093.2017.11.016
2017-01-05
國(guó)家自然科學(xué)基金項(xiàng)目(51409047、61403150)
周煥銀(1975—), 女, 副教授, 碩士生導(dǎo)師。 E-mail: hyzou@ecit.cn

