減振器動剛度特性研究

李世堯， 張衛國， 侯軍占， 段文博， 遲圣威， 郭冰濤

(西安應用光學研究所， 陜西 西安 710065)

減振器動剛度特性研究

李世堯， 張衛國， 侯軍占， 段文博， 遲圣威， 郭冰濤

(西安應用光學研究所， 陜西 西安 710065)

動剛度特性是減振器設計及選型的重要指標，通過改變減振器剛度和阻尼，使系統避開共振區間，以發揮減振器最佳減振效果是目前的研究重點。針對目前減振器動剛度特性研究較少的情況，提出一種減振器的動剛度計算方法。通過靜力實驗獲取加載和卸載的變形- 力曲線，擬合得出減振器靜剛度值；根據靜剛度值和單自由度系統動剛度計算公式獲得動剛度隨頻率變化規律；設計減振器動剛度驗證實驗。研究結果表明：該動剛度計算結果和實驗結果吻合情況較好，誤差平均值在6%以內，可為實際工程的減振器選型及應用提供參考。

機械學； 靜剛度； 動剛度； 橡膠減振器； 鋼絲繩減振器

0 引言

振動引起的動態變形和動態應力，容易引起機械結構疲勞和破壞，或引起連接部件間的微振磨損、縮短零件使用壽命。為了隔離振動，需要使用減振器來吸振[1]。工程設備中的減振元件多采用橡膠減振器和鋼絲繩減振器[2]。目前，減振器廣泛應用于機載光電轉塔、艦艇導彈發射裝置、導航裝置等領域。

減振器的設計及選型需要重點考慮其動剛度特性。結構在外部力作用下抵抗變形的能力即為剛度，它可以分為靜剛度和動剛度。動剛度是指動載荷下抵抗變形的能力，即引起單位振幅所需要的動態力[3]。動剛度特性是動剛度隨著頻率變化的規律，研究系統動剛度特性，結合實際工程中系統工作環境要求，通過改變減振器剛度和阻尼，可以使系統避開共振區間，以達到隔離振動的目的。和法家等[3]以某橡膠減振器為研究對象，將橡膠減振器的振動頻率、振幅、預載荷3個水平因素作為可變參數，進行循環振動實驗，具體地了解了動剛度的影響因素。該方法記錄力- 位移信號獲得約30 000個數據，實驗方法復雜，耗時較長，數據量大。萬葉青等[4]對鋼絲繩隔振器的靜力曲線使用了多項式擬合的方法來描述，推導了動態參數識別的過程，并將靜特性實驗獲得的參數用于動態特性分析和振動響應分析。周桐等[5]通過實驗，研究了3種不同剛度的鋼絲繩隔振器兼顧隔振、隔沖和抗過載的綜合能力，實驗結果表明，剛度較大的隔振器在承受高量級隨機激勵時具有一定的隔振能力，抗沖擊性能較好。目前對減振器的抗振性能研究很多，但對減振器的動剛度特性研究較少，實際工程中大多只考慮靜剛度特性，或采用按經驗對動剛度估值或在一定范圍內試錯的方法[6]。動剛度主要是通過實驗方法獲得，耗時較長，而且一旦剛度和阻尼等參數發生改變就需要重新做實驗，復雜繁瑣，效率低下[7-14]。

針對以上問題，本文提出了一種減振器動剛度計算方法。通過該方法可以在減振器選型階段獲得減振器動剛度特性，通過分析其共振區間和振動放大率，可為系統選擇合適的減振器提供參考，縮小減振器選擇范圍。

1 靜力特性研究

對于受簡諧激振力的單自由度系統， 其動剛度KD可表示為

KD=K[(1-λ2)+2iζλ]，

(1)

式中：K為系統靜剛度；λ為激勵頻率與系統固有頻率的頻率比；ζ為阻尼比[15]。

從(1)式中可知，為了分析減振器的動剛度特性，首先要得到減振器較為準確的靜剛度值[4]。

本文以機載光電轉塔常用的兩種減振器為研究對象，這兩種減振器分別為天然橡膠減振器和螺旋形鋼絲繩減振器，如圖1所示。對這兩種減振器進行靜力加載實驗，設計減振器夾具工裝如圖2所示，靜力拉伸實驗裝置如圖3所示。

圖1 機載光電轉塔的兩種常用減振器Fig.1 Two vibration isolators for electro-optic turret

圖2 減振器夾具工裝Fig.2 Vibration isolator fixture

圖3 靜力實驗裝置Fig.3 Static mechanic experimental instruments

設置靜力實驗對4個減振器進行靜力拉伸和卸載，拉伸力的最大值為500 N. 為保證實驗結果準確，靜力實驗加載速度要求足夠慢，分別取0.2 mm/min、0.4 mm/min、0.6 mm/min、0.8 mm/min進行實驗，實驗結果相差不大；大于0.8 mm/min之后實驗結果出現誤差。在此，為提高實驗效率，取加載和卸載速度為0.6 mm/min. 實驗測得的兩種減振器負載F與變形x曲線如圖4所示。

圖4 靜力實驗結果Fig.4 Static mechanic experimental result

從圖4中可以看出，由于阻尼的作用，兩種減振器中負載與變形都呈遲滯迴線分布。從圖4(a)和圖4(b)可以看出，相對于橡膠減振器，由于鋼絲繩減振器鋼絲之間的相對滑移產生了摩擦阻力，所以遲滯迴線包圍的面積更大[16]。

要分析減振器的靜剛度值，假定減振器的阻尼，剛度和質量的特性在允許的使用期限內，并不隨著時間的推移而發生變化；而且質點運動時，系統能量呈現耗散特征，因此可以假設系統是一個保守的自治系統[4]。按照以上假設，就可以把減振器的靜剛度值識別出來。

安裝減振器的系統可以簡化為單自由度的質量- 彈簧- 阻尼模型，系統可以用微分方程(2)式來描述：

(2)

式中：x為減振器的變形量；m為減振器質量；c、k分別為減振器的阻尼系數和剛度系數；fμ為減振器內部摩擦阻力；F為系統輸入力。

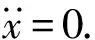
加載和卸載時力的方向相同，但速度方向相反。

加載時：

(3)

卸載時：

(4)

式中：fL(x,0)、fU(x,0)分別表示加載速度趨于零加載和卸載過程中設備施加在減振器兩端的拉力。

由(3)式和(4)式可得

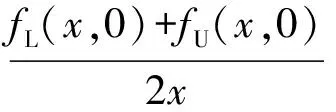
(5)

由于減振器的靜力曲線比較復雜， 一些典型函數不能準確地描述。在數學上，多項式擬合是用來逼近復雜數據的有效工具，運用多項式可以較為準確地描述許多復雜的曲線。不過在使用多項式擬合過程中，有可能會出現高次擬合的震蕩現象和無解的情況。所以并不一定擬合次數選取的越多越好， 應當在確保計算精度的同時，必須適當地控制多項式的次數[4]。

對于天然橡膠減振器，其加載部分的曲線擬合為5次多項式結果：

fL(x,0)=0.024 79x5-0.443 7x4+3.042x3-
11.23x2+89.83x+11.01.

(6)

擬合曲線相關系數為0.999 7，剩余標準差為1.485 N.

卸載部分的曲線擬合為5次多項式結果：

fU(x,0)=0.083 98x5-1.463x4+9.099x3-
21.05x2+65.99x+1.925.

(7)

擬合曲線相關系數為0.999 8，剩余標準差為1.172 N. 以上結果表明兩條曲線的擬合精度較高。

將(6)式和(7)式代入(5)式可得天然橡膠減振器靜剛度Kr滿足：

Krx=0.054 4x5-0.953 4x4+6.070 5x3-
16.140 0x2+77.910 0x+6.467 5.

(8)

對此剛度曲線進行1次函數擬合，可得到其斜率Kr=65.3 N/mm，擬合曲線如圖5所示。

圖5 剛度系數擬合曲線Fig.5 Fitted curves of stiffness coefficient

同理可以得到螺旋形鋼絲繩減振器的靜剛度值Kw=373.3 N/mm.

2 動剛度特性研究

根據受簡諧激振力的單自由度系統動剛度計算公式(1)式可知，動剛度的幅值Kd為

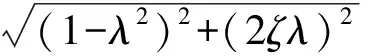
(9)

對于某天然橡膠減振器，剛度為65.3 N/mm，質量為0.092 kg, 廠家提供的阻尼比為0.075. 作為負載的配重塊質量為3.176 kg. 根據單自由度固有頻率公式

(10)

此時m為減振器和配重塊的質量之和，得到此時的固有頻率為22.49 Hz.

在Matlab中進行計算，根據(9)式繪制該橡膠減振器的動剛度Kd隨頻率f變化規律，如圖6所示。

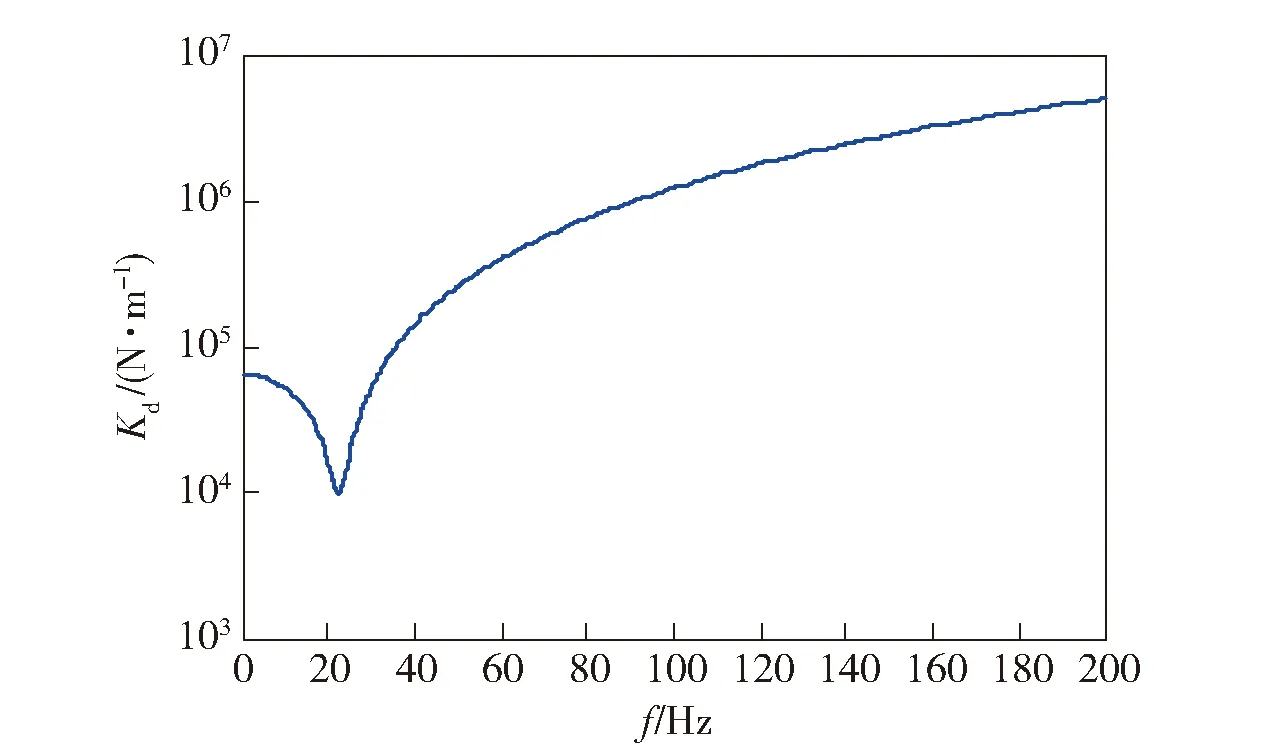
圖6 天然橡膠減振器動剛度計算曲線Fig.6 Calculated dynamic stiffness curve of dynamic Stiffness

同理可繪制螺旋形鋼絲繩減振器的動剛度隨頻率變化規律。為驗證該計算動剛度的準確性，需要將計算動剛度與實驗測得的動剛度進行比較。對兩種減振器進行掃頻實驗，以測得兩種減振器的動剛度。實驗原理如圖7所示。

圖7 實驗原理圖Fig.7 Schematic diagram of experimental set-up

實驗采用德國M+P公司的128通道振動控制模態測試分析系統進行步進正弦掃頻實驗。M+P振動控制測試分析系統主要由M+P Vibrunner測試系統、Dytran三向加速度傳感器、Dytran力錘及M+P Smart Office振動模態測試分析軟件模塊組成，如圖8所示。通過該系統可以實現輸入力控制、加速度采集和頻域分析等功能。實驗裝置如圖9所示。

圖8 M+P振動控制測試分析系統Fig.8 M+P vibration control analysis system

圖9 步進正弦掃頻實驗Fig.9 Stepped sine sweep experiment

采用如圖9所示的激振器對減振器一端輸入激振力，在減振器的激振力輸入端布置力傳感器，在兩端分別布置加速度傳感器。激振頭與減振器、減振器與配重塊之間都通過螺釘連接。大多數使用減振器的工程設備關注減振器在頻率0～200 Hz之間的隔振效果，掃頻實驗設置起始頻率0 Hz，終止頻率200 Hz，頻率增量為0.001 Hz，采樣率1 024 Hz，激振力的幅值為15 N.

實驗得到的數據有3組，分別為輸入力F，輸入端加速度ai和輸出端加速度ao，M+P振動控制測試分析系統的Smart Office軟件可直接將傳感器測得的數據進行處理，得到輸入端加速度和輸出端加速度關于輸入力的頻響函數Hi和Ho為

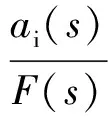
(11)

式中：ai(s)、ao(s)和F(s)分別為ai、ao和F經過拉普拉斯變換后的表達式。通過輸入端和輸出端加速度的差值獲得相對加速度Δa(s)為

Δa(s)=ai(s)-ao(s)=(Hi-Ho)F(s).

(12)

相對加速度Δa(s)關于輸入力的頻響函數即為Hi與Ho的差值ΔH，即

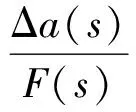
(13)

對于單自由度系統的運動微分方程(2)式兩邊作傅里葉變換得

Z(s)X(s)=F(s)，

(14)

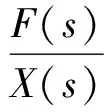
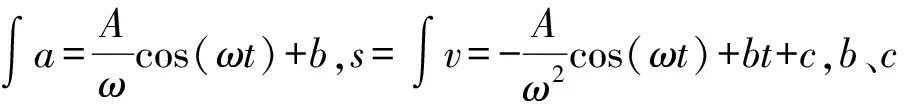
當初始條件t=0時，v=0，s=0，則b=c=0，

(15)

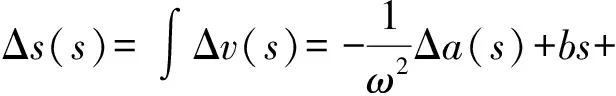
(16)

所以：

(17)

對于動剛度Kd有

(18)

將實驗得出的頻響函數導入Matlab中，根據(18)式計算得出天然橡膠減振器的動剛度隨頻率變化規律。實驗動剛度與計算動剛度對比如圖10所示。

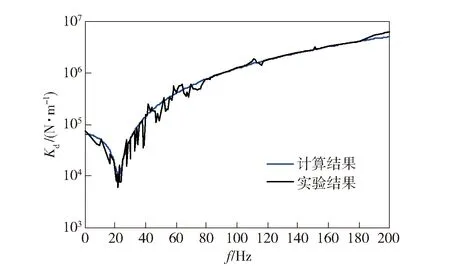
圖10 天然橡膠減振器的動剛度Fig.10 Dynamic stiffness of rubber shock absorber

從圖10中可以看出，計算曲線與實驗曲線吻合較好。為判斷計算曲線和實驗曲線計算曲線的接近程度，計算二者的誤差平均值。誤差平均值的計算方式是：每隔0.1 Hz分別取實驗曲線和計算曲線上的兩個值，取計算曲線相對于實驗曲線的誤差絕對值，然后將整個頻段的所有誤差絕對值取平均。最后得到了計算曲線與實驗曲線的誤差平均值為5.34%，計算動剛度的最小值為9.767 4 N/mm，實驗動剛度的最小值為9.578 3 N/mm，誤差為1.97%.

根據計算得到的螺旋形鋼絲繩減振器的固有頻率和廠家提供的阻尼比如表1所示。同理，將螺旋形鋼絲繩減振器的計算動剛度和實驗結果進行對比，如圖11所示。

表1 減振器固有頻率與阻尼比

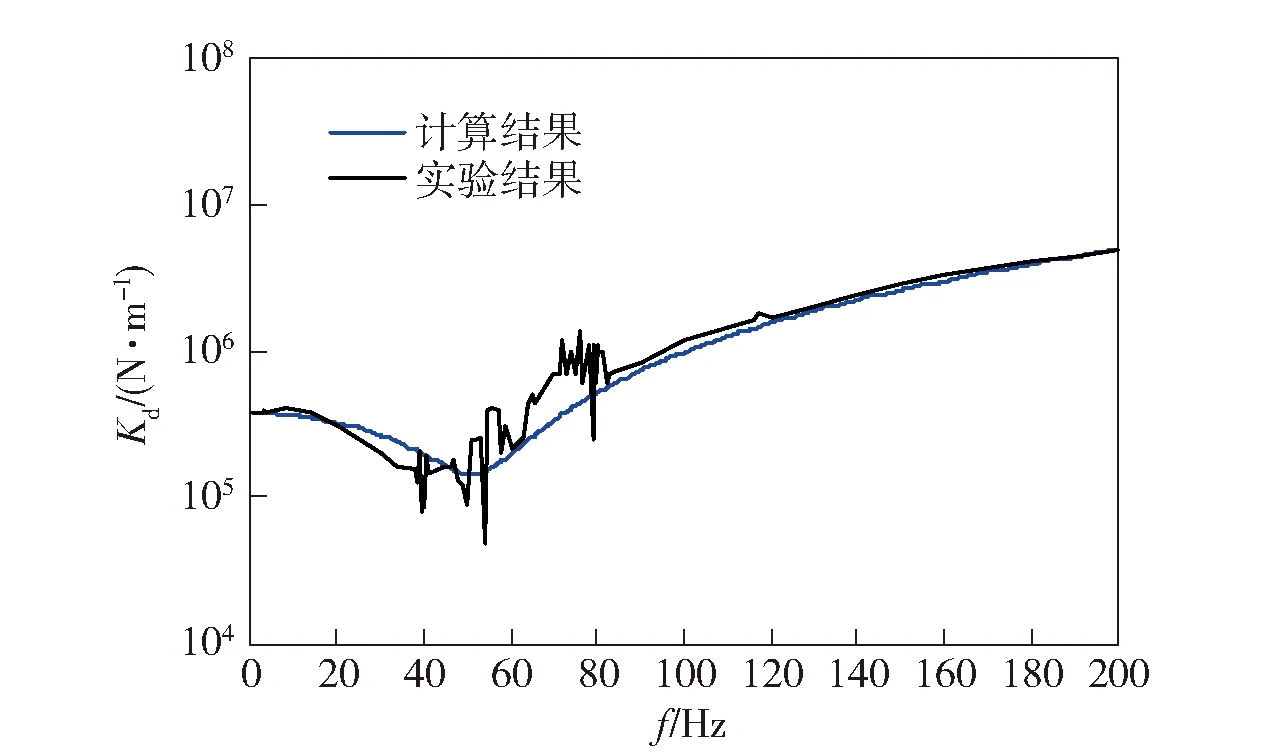
圖11 螺旋形鋼絲繩減振器的動剛度Fig.11 Dynamic stiffness of spiral steel wire rope isolator

螺旋形鋼絲繩減振器計算曲線與實驗曲線吻合較好，誤差平均值為4.33%. 兩種減振器的靜剛度、動剛度最小值和動剛度平均值整理如表2所示。

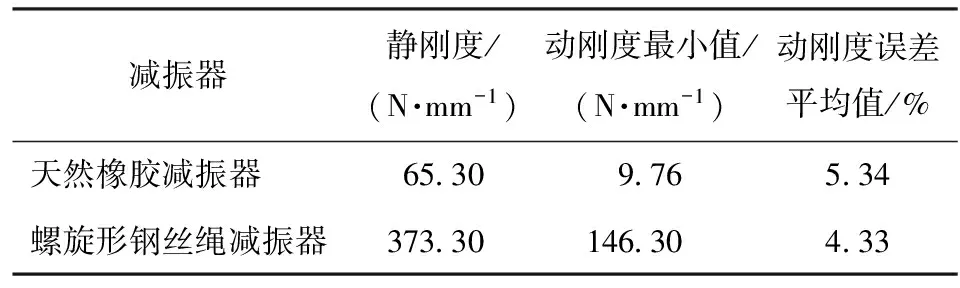
表2 兩種減振器的靜剛度與動剛度比較

3 結論

本文對兩種常用減振器的動剛度特性進行了研究，提出一種減振器動剛度計算方法，得出以下結論：

1) 基于靜剛度實驗所獲的力- 變形曲線，結合單自由度系統動剛度計算公式，可以獲得減振器動剛度特性的理論分析方法。

2) 開展了減振器動剛度實驗研究，結果顯示，橡膠減振器的測試結果和理論計算結果的誤差平均值為5.34%，鋼絲繩減振器測試結果和理論計算結果的誤差平均值為4.33%，驗證了該方法的準確性。

3) 在機載光電轉塔中選用減振器，采用該方法可提高減振器選型效率，減少減振器的安裝與拆卸過程。但本文方法未考慮成組減振器的動剛度特性，以及安裝預緊力、溫度等因素對動剛度特性的影響，這些工作還需要進一步的研究。

References)

[1] 班書昊, 李曉艷, 蔣學東, 等. 鋼絲繩隔振器的非線性動力學模型[J]. 力學與實踐, 2012, 34(1): 66-69.

BAN Shu-hao, LI Xiao-yan, JIANG Xue-dong, et al.Nonlinear dynamic model on steel wire isolator[J]. Mechanics in Engineering, 2012, 34(1):66-69. (in Chinese)

[2] 秦震,周素霞,孫晨龍,等. 減振器特性參數對高速動車組臨界速度的影響研究[J]. 機械工程學報, 2017, 53(6): 138-144.

QIN Zhen, ZHOU Su-xia, SUN Chen-long, et al. Research on influence of the characteristic parameters of the shock absorber on critical velocity of high-speed train[J]. Journal of Mechanical Engineering, 2017,53(6): 138-144. (in Chinese)

[3] 和法家, 盧曦. 某直升機橡膠減振器動剛度特性實驗[J]. 實驗室研究與探索, 2014, 33(3): 42-44.

HE Fa-jia, LU Xi.Experimental research on dynamic stiffness characteristics of a rubber isolator[J]. Research and Exploration in Laboratory, 2014, 33(3):42-44. (in Chinese)

[4] 萬葉青, 范立民, 齊煜. 鋼絲繩隔振器非線性特性分析[J]. 振動與沖擊, 2007, 26(7):46-49.

WAN Ye-qing, FAN Li-min, QI Yu. Nonlinear characteristics analysis for steel wire isolators[J]. Journal of Vibration and Shock, 2007, 26(7):46-49. (in Chinese)

[5] 周桐, 劉青林, 張思剪. 鋼絲繩隔振器綜合力學性能實驗研究[J].振動與沖擊, 2007, 26(9): 55-60.

ZHOU Tong, LIU Qing-lin, ZHANG Si-jian. Simplified model analysis of wire-rope vibration isolator[J]. Journal of Vibration and Shock, 2007, 26(9): 55-60.(in Chinese)

[6] 王杰方, 安偉光, 蔣運華. 超空泡運動體結構的隨機動剛度特性分析[J]. 兵工學報, 2013, 34(9): 1103-1108.

WANG Jie-fang, AN Wei-guang, JIANG Yun-hua. Analysis of random dynamic stiffness characteristics of supercavitating vehicle structure[J]. Acta Armamentarii, 2013, 34(9): 1103-1108.(in Chinese)

[7] 劉興天, 鐘鳴, 申軍烽, 等. 松弛型阻尼隔振模型的動剛度實驗研究[J]. 噪聲與振動控制, 2016, 36(5):180-182.

LIU Xing-tian, ZHONG Ming, SHEN Jun-feng, et al. Experimental analysis of the dynamic stiffness of a vibration isolation system with relaxation type damping[J]. Noise and Vibration Control, 2016, 36(5):180-182. (in Chinese)

[8] 周生通, 李鴻光, 劉巖, 等. 重型動平衡機擺架的動剛度測試與動力特性預計[J].機械工程學報, 2014, 50(8):1-8.

ZHOU Sheng-tong, LI Hong-guang, LIU Yan, et al. Dynamic stiffness measurement and dynamic behaviors prediction of bearing support in heavy dynamic balancing machine[J]. Journal of Mechanical Engineering, 2014, 50(8):1-8. (in Chinese)

[9] Pesterev A V, Bergman L A. An improved series expansion of solution to the moving oscillator problem[J]. Vibration and Acoustics, 2000, 122(1):54-61.

[10] Lekueh H. Shock and vibration isolation in severe environments[J]. Noise and Vibration Control World-wide, 1986, 17(8):66-70.

[11] Ni Y Q, Ko J M, Wong C W. Modeling and identification of a wire-cable vibration isolator via a cyclic loading test[J]. Proceedings of the Institution of Mechanical Engineers, 1999, 213(3): 163-171.

[12] 李超, 李志遠. 彈性元件低頻動剛度測試方法研究[J].農業裝備與車輛工程, 2016, 54(7):42-45.

LI Chao, LI Zhi-yuan. Test method analysis of dynamic stiffness of resilient supports in low frequency[J]. Agricultural Equipment & Vehicle Engineering, 2016, 54(7):42-45.(in Chinese)

[13] 金翔, 李蓓智. 高速電主軸動剛度的計算與測試方法[J]. 現代制造工程, 2016(5):40-45.

JIN Xiang, LI Bei-zhi. Studies on the dynamic stiffness of high speed spindle supporting components[J]. Modern Manufacturing Engineering, 2016(5):40-45. (in Chinese)

[14] 謝宏偉,陶忠,侯軍占,等. 多繩精密傳動的傳動精度實驗研究[J]. 兵工學報,2017,38(4):728-734.

XIE Hong-wei, TAO Zhong, HOU Jun-zhan, et al. Experimental research on transmission accuracy of multi-cable drive[J]. Acta Armamentarii, 2017,38 (4): 728-734. (in Chinese)

[15] 薛碧杰. 索梁結構的熱致振動及動剛度分析[D]. 西安:西安電子科技大學, 2014.

XUE Bi-jie. Analysis onthermally induced vibration and dynamic stiffness of cable-beam structures[D]. Xi’an: Xidian University, 2014.(in Chinese)

[16] 黃華, 盧曦, 余慧杰. 基于Ansys與iSIGHT的橡膠減振器遲滯回線仿真研究[J]. 現代制造工程, 2014(12):59-63.

HUANG Hua, LU Xi, YU Hui-jie. Simulation research of the rubber damper hysteresis loop under harmonic load based on Ansys and iSIGHT[J]. Modern Manufacturing Engineering, 2014(12):59-63.(in Chinese)

ResearchonDynamicStiffnessofVibrationIsolator

LI Shi-yao, ZHANG Wei-guo, HOU Jun-zhan, DUAN Wen-bo, CHI Sheng-wei, GUO Bing-tao

(Xi’an Institute of Applied Optics, Xi’an 710065, Shaanxi, China)

Dynamic stiffness is a crucial characteristic of vibration isolator. A method to calculate the dynamic stiffness of vibration isolator is proposed. The static stiffness is concluded from the experimental deformation-force curve. Dynamic stiffness is calculated by using single degree of freedom (SDOF) dynamic stiffness formula. An experiment is designed to verify the calculated results. Experimental results show that the deviation between calculated result and the experimental result is within 6%. The proposed method is effective and applicable for dynamic analysis of vibration isolators.

mechanics; static stiffness; dynamic stiffness; rubber isolator; steel wire rope isolator

O328

A

1000-1093(2017)11-2274-06

10.3969/j.issn.1000-1093.2017.11.026

2017-04-20

國家國防科技工業局技術基礎科研項目(A0920132001)；兵器“十二五”預先研究基金項目(62201070139)；高等院校協同創新合作專項項目(KH201504)

李世堯(1991—)，男，碩士研究生。E-mail:lsyyywd@163.com

張衛國(1975—)，男，研究員，碩士生導師。E-mail:zzwwgg1975@163.com