對一道高考題的探究

湖北 聶文喜

對一道高考題的探究

湖北 聶文喜

( )

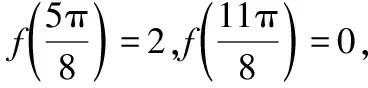
本題以三角函數(shù)為載體，以對稱軸、對稱中心、最小正周期為切入點，主要考查學(xué)生數(shù)學(xué)基本知識、數(shù)學(xué)方法、數(shù)學(xué)思想的掌握情況，考查分析問題和解決問題的綜合能力，入口較寬，解法多樣，同時又能區(qū)分不同思維層次的學(xué)生,本文嘗試從不同視角尋求突破．

1.解法探究

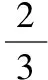
【點評】逐一驗證法是解答選擇題的一種方法，主要是從結(jié)論反代，看是否適合條件.由于數(shù)學(xué)選擇題答案的唯一性，只要判斷一個選擇支正確即可.

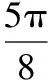
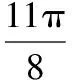
又f(x)最小正周期大于2π，

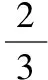
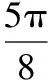
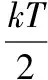
2．題源探究

( )

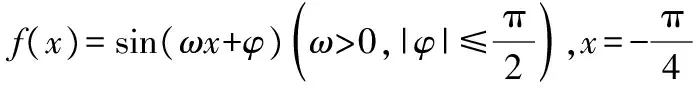
A．11 B．9

C．7 D．5

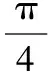
故函數(shù)f(x)的最小正周期為T=π．

【點評】已知函數(shù)f(x)=Asin(ωx+φ)(A,ω,φ為常數(shù)，Agt;0，ωgt;0)，則

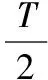
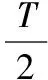
3．變式探究

( )

( )

( )

( )

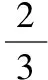
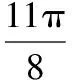
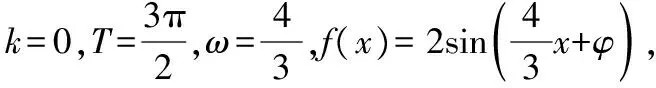
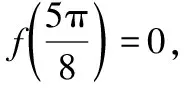
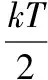
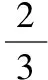
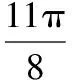
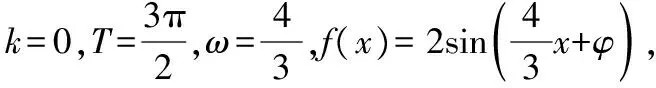
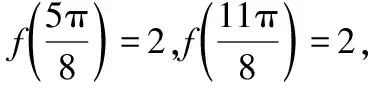
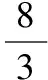
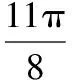
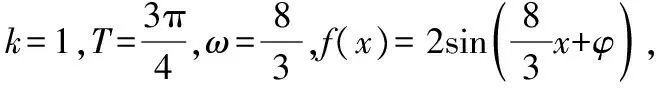
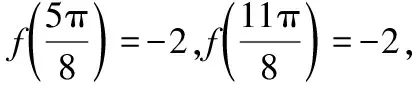
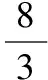
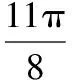
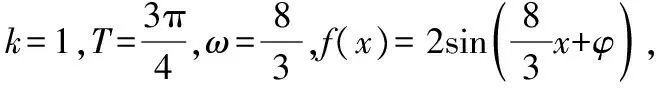
【點評】已知函數(shù)f(x)=Asin(ωx+φ)(A,ω,φ為常數(shù)，Agt;0，ωgt;0)，則

(1)若x=x1和x=x2均為函數(shù)f(x)圖象的對稱軸，且f(x1)=f(x2)，則|x2-x1|=kT(k∈Z，T為f(x)的最小正周期)；

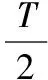
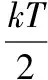
4．拓展探究

上述高考題及變式題中x=x1和x=x2均為函數(shù)f(x)的對稱軸或零點，若x=x1和x=x2中有一個不是函數(shù)對稱軸或零點，情況如何呢？

( )

( )

( )

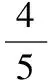
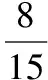
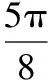
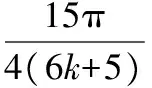
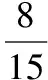
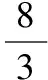
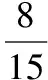
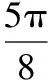
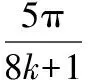
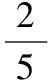
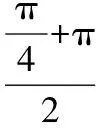
湖北省廣水市第一高級中學(xué))