一道全國(guó)高考真題的變式探究與推廣

安徽 楊續(xù)亮 蘇岳祥

一道全國(guó)高考真題的變式探究與推廣

安徽 楊續(xù)亮 蘇岳祥

一、試題再現(xiàn)

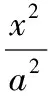
(Ⅰ)求C的方程；

(Ⅱ)設(shè)直線(xiàn)l不經(jīng)過(guò)P2點(diǎn)且與C相交于A，B兩點(diǎn)，若直線(xiàn)P2A與直線(xiàn)P2B的斜率的和為-1，證明：l過(guò)定點(diǎn)．

二、試題規(guī)律分析

三、試題解法賞析

下面對(duì)本題的第二問(wèn)作些探究：

證法一：直線(xiàn)方程的斜截式視角

設(shè)直線(xiàn)P2A和直線(xiàn)P2B的斜率分別為k1,k2且k1+k2=-1，

①當(dāng)直線(xiàn)l的斜率不存在時(shí)，設(shè)l:x=t由題設(shè)知|t|lt;2且t≠0，A(t,yA),B(t,-yA)，

得t=2，此時(shí)l過(guò)橢圓右頂點(diǎn)，不存在兩個(gè)交點(diǎn)，故不滿(mǎn)足．

②當(dāng)直線(xiàn)l的斜率存在時(shí)，設(shè)l∶y=kx+m(m≠1)，A(x1，y1)，B(x2，y2)，

整理得(1+4k2)x2+8kmx+4m2-4=0，

=-1，

又m≠1,所以m=-2k-1，

此時(shí)Δ=-64k，存在klt;0使得Δgt;0成立．

所以直線(xiàn)l的方程為y=kx-2k-1，

當(dāng)x=2時(shí)，y=-1，所以l過(guò)定點(diǎn)(2，-1)．

證法二：平移坐標(biāo)系視角

因?yàn)橹本€(xiàn)P2A與直線(xiàn)P2B的斜率的和為-1，

所以2m-2n=1，平移后得直線(xiàn)經(jīng)過(guò)定點(diǎn)(2，-2)，平移前的直線(xiàn)方程為m-2n=1,

所以平移前的直線(xiàn)經(jīng)過(guò)點(diǎn)(2，-1).

【評(píng)注】這種解法，很好地體現(xiàn)了減元思想和整體思想，在設(shè)定直線(xiàn)l的方程也可以設(shè)為點(diǎn)斜式，兩點(diǎn)式直接求解.

四、試題的變式探究

(Ⅰ)求橢圓C的方程；

(Ⅱ)E,F是橢圓C上的兩個(gè)動(dòng)點(diǎn)，如果直線(xiàn)AE的斜率與AF的斜率互為相反數(shù)，證明直線(xiàn)EF的斜率為定值，并求出這個(gè)定值.

又直線(xiàn)AF的斜率與AE的斜率互為相反數(shù)，

在上式中以-k代k，可得

所以直線(xiàn)EF的斜率

【評(píng)注】直線(xiàn)AE的斜率與AF的斜率互為相反數(shù)時(shí)，即k1+k2=0時(shí)，直線(xiàn)EF的斜率為定值.

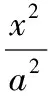
(Ⅰ)求橢圓C的方程；

(Ⅱ)當(dāng)r變化時(shí)，①求k1·k2的值；②試問(wèn)直線(xiàn)BD是否過(guò)某個(gè)定點(diǎn)？若是，求出該定點(diǎn)；若不是，請(qǐng)說(shuō)明理由.

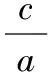
又a2-b2=c2，

對(duì)于直線(xiàn)AD:y=k2x+1，

于是k1,k2是方程(1-r2)k2-2k+1-r2=0的兩實(shí)根，故k1·k2=1.

考慮到r→1時(shí)，D是橢圓的下頂點(diǎn)，B趨近于橢圓的上頂點(diǎn)，故BD若過(guò)定點(diǎn)，則猜想定點(diǎn)在y軸上.

直線(xiàn)BD的方程為

令x=0，

【評(píng)注】直線(xiàn)AB,AD的斜率之積為k1k2=1為定值時(shí)，直線(xiàn)BD過(guò)定點(diǎn).

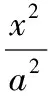
(Ⅰ)求橢圓C的標(biāo)準(zhǔn)方程;

(Ⅱ)設(shè)N(0,2),過(guò)點(diǎn)P(-1,-2)作直線(xiàn)l交橢圓C異于N的A，B兩點(diǎn)，直線(xiàn)NA，NB的斜率為k1,k2，證明k1+k2為定值.

由余弦定理得

|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|cos60°

=(|MF1|+|MF2|)2-2|MF1||MF2|(1+cos60°),

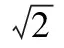
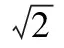
由|F1F2|=4得c=2,從而b=2.

(Ⅱ)證明:當(dāng)直線(xiàn)l的斜率存在時(shí)，設(shè)斜率為k，

得(1+2k2)x2+4k(k-2)x+2k2-8k=0，

設(shè)點(diǎn)A(x1,y1)，B(x2,y2)，

=4，

綜上，k1+k2=4為定值.

【評(píng)注】過(guò)點(diǎn)P(-1,-2)作直線(xiàn)l交橢圓C異于N(0,2)的A，B兩點(diǎn)，直線(xiàn)NA，NB的斜率為k1,k2，可以得到k1+k2為定值.

從2017年全國(guó)卷高考試題和3個(gè)變式我們得到如下結(jié)論：

在這個(gè)問(wèn)題中，如P是橢圓上的一點(diǎn)，A,B是兩動(dòng)點(diǎn)，那么，PA,PB斜率之和為定值時(shí)或者之積為定值時(shí)，直線(xiàn)AB是否經(jīng)過(guò)定點(diǎn)呢？通過(guò)探究，發(fā)現(xiàn)：

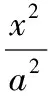
從變式試題可以看出，這里的4個(gè)結(jié)論逆命題同樣成立，只是敘述的方式上稍作調(diào)整，請(qǐng)讀者自己完成.

五、試題的類(lèi)比探究

【變式4】已知拋物線(xiàn)C：y2=2px(pgt;0)的焦點(diǎn)F(1，0)，O為坐標(biāo)原點(diǎn)，A，B是拋物線(xiàn)C上異于O的兩點(diǎn).

(Ⅰ)求拋物線(xiàn)C的方程；

所以?huà)佄锞€(xiàn)C的方程為y2=4x.

(Ⅱ)證明:①當(dāng)直線(xiàn)AB的斜率不存在時(shí)，

所以A(8，t)，B(8，-t)，此時(shí)直線(xiàn)AB的方程為x=8.

②當(dāng)直線(xiàn)AB的斜率存在時(shí)，設(shè)其方程為y=kx+b(k≠0)，設(shè)點(diǎn)A(x1,y1)，B(x2,y2),

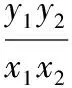
即y=k(x-8).

綜上所述，直線(xiàn)AB過(guò)定點(diǎn)(8，0).

過(guò)拋物線(xiàn)y2=2px上點(diǎn)的任意一點(diǎn)P(x0,y0)作兩條直線(xiàn)PA,PB與拋物線(xiàn)交于點(diǎn)A,B，其中，PA,PB,AB斜率都存在，分別記作k1,k2,k,則有如下結(jié)論：

讀者可以參照2017年全國(guó)理20和變式題的證明方法證明這三個(gè)結(jié)論.

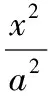
(Ⅰ)求橢圓C的標(biāo)準(zhǔn)方程;

(Ⅱ)若直線(xiàn)l:y=kx+m與橢圓C相交于A，B兩點(diǎn)(于A，B不是左右頂點(diǎn))，且以AB為直徑的圓過(guò)橢圓C的右頂點(diǎn)，求證直線(xiàn)l過(guò)定點(diǎn)，并求出該定點(diǎn)的坐標(biāo).

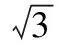
(Ⅰ)求軌跡C的方程.

安徽省安慶市岳西縣湯池中學(xué))