統計與概率知識的綜合應用
李慧祥
統計與概率知識的綜合應用
李慧祥
將統計與概率的知識綜合在一起考查,是近年來中考命題的一個新趨勢.現以2017年中考數學試題為例來說明,希望能引起同學們對這個命題新趨勢的重視,認真研究這類問題的結構特征,切實掌握這類問題的求解思路.
例1 (2017·安徽)甲、乙、丙三位運動員在相同條件下各射靶10次,每次射靶的成績如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根據以上數據完成下表:
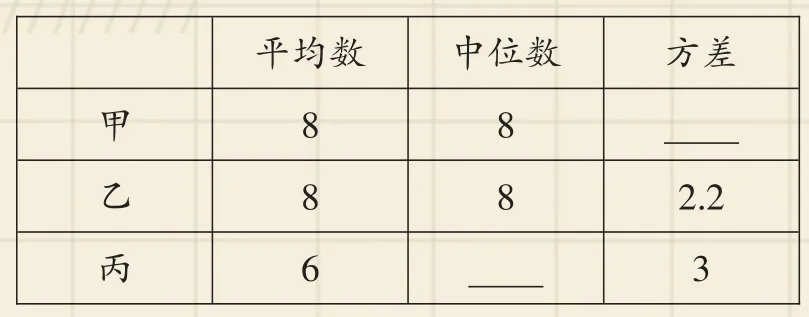
平均數中位數方差2.2 3甲乙丙8 8 6 8 8
(2)根據表中數據分析,哪位運動員的成績最穩定,并簡要說明理由;
(3)比賽時三人依次出場,順序由抽簽方式決定,求甲、乙相鄰出場的概率.
(2)∵甲的方差是2,乙的方差是2.2,丙的方差是3,S甲2<S乙2<S丙2,∴甲運動員的成績最穩定;
式中:Nii,Hii以及Jii分別表示矩陣N,H,J的第i行第i列的元素;m為量測向量的維數;Fk+1為狀態方程的jacobian矩陣;ωk+1為殘差,η為遺忘因子,取值在0~1之間,通常取為0.95。
(3)畫樹狀圖如下:
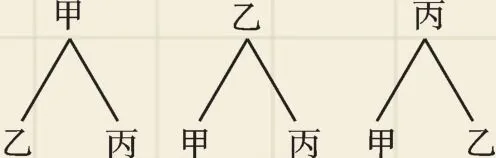
根據樹狀圖可知,共有6種等可能情況,甲、乙相鄰出場的情況有4種,
【點評】本題綜合考查方差、平均數、中位數和概率計算等知識.解題時既要準確運用統計知識求中位數和方差,又要能應用方差的本質——反映一組數據的波動大小,方差越小越穩定來做出判斷,同時還要能熟練地運用畫樹狀圖或列表來求概率.
例2 (2017·蘇州)初一(1)班針對“你最喜愛的課外活動項目”對全班學生進行調查(每名學生分別選一個活動項目),并根據調查結果列出統計表,繪制成扇形統計圖.
男、女生所選項目人數統計表
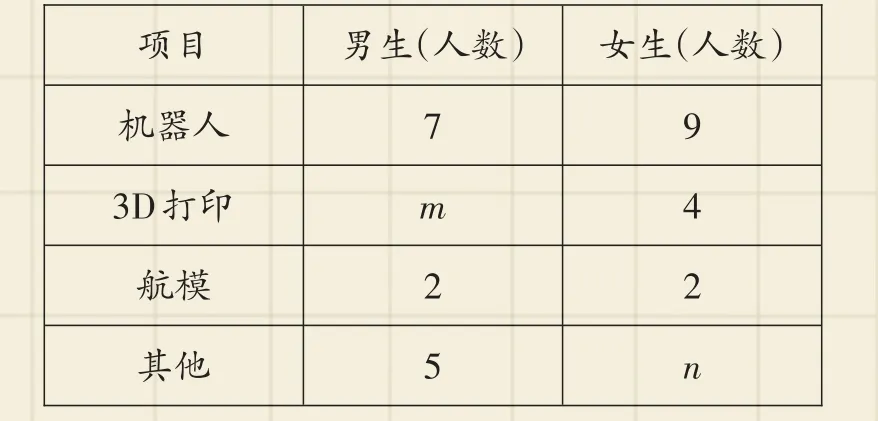
項目機器人3D打印航模其他男生(人數)7 m 2 5女生(人數)9 4 2 n
根據以上信息解決下列問題:
(2)扇形統計圖中機器人項目所對應扇形的圓心角度數為 °;

(3)從選航模項目的4名學生中隨機選取2名學生參加學校航模興趣小組訓練,請用列舉法(畫樹狀圖或列表)求所選取的2名學生中恰好有1名男生、1名女生的概率.
【解析】(1)由兩種統計表可知總人數=4÷10%=40(人),∵3D打印項目占30%,∴3D打印項目人數=40×30%=12(人),∴m=12-4=8,∴n=40-16-12-4-5=3;
(3)根據題意列表如下:
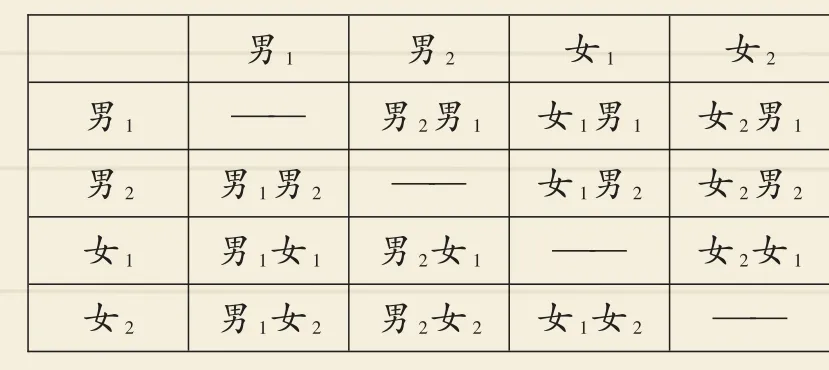
女2女2男1女2男2女2女1——男1男2女1女2男1——男1男2男1女1男1女2男2男2男1——男2女1男2女2女1女1男1女1男2——女1女2
由表可知,共有12種等可能的結果,其中“1名男生、1名女生”有8種可能,∴P(所選取的2名學生中恰好有1名男生、1名女生)=
【點評】本題主要考查統計中圖表信息的讀取與運用、用列表與樹狀圖求概率等知識.解題時需將統計表與統計圖結合起來思考.此外,這里隨機選取2名學生是“無放回”事件,表格中不能出現“男1男1”“男2男2”“女1女1”“女2女2”的情形.
例3 (2017·安順)隨著交通道路的不斷完善,帶動了旅游業的發展,某市旅游景區有A、B、C、D、E等著名景點,該市旅游部門統計繪制出2017年五一長假期間旅游情況統計圖,根據以下信息解答下列問題:
某市2017年五一長假期間旅游情況統計圖
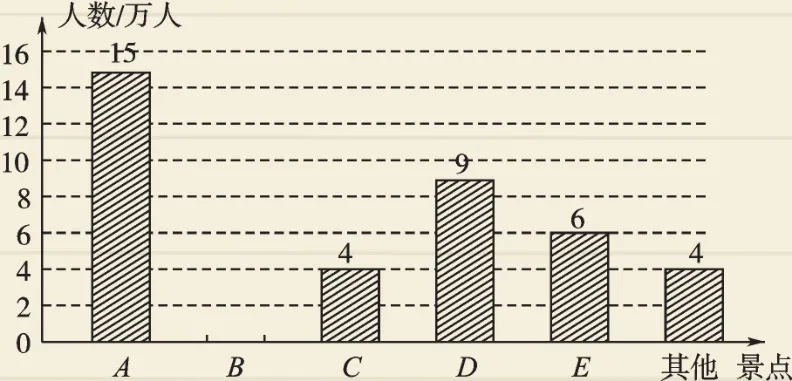
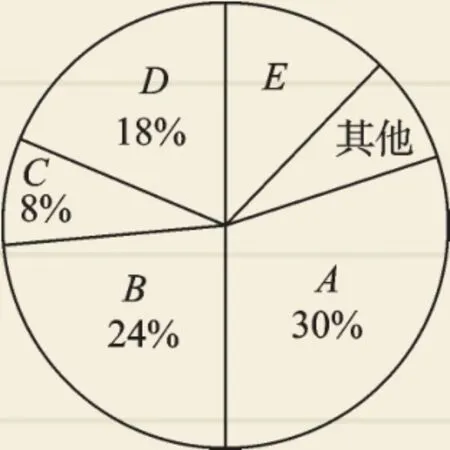
(1)2017年五一期間,該市周邊景點共接待游客_______萬人,扇形統計圖中A景點所對應的圓心角的度數是_______,并補全條形統計圖.
(2)根據近幾年到該市旅游人數增長趨勢,預計2018年五一節將有80萬游客選擇該市旅游,請估計有多少萬人會選擇去E景點旅游?
(3)甲、乙兩個旅行團在A、B、D三個景點中,同時選擇去同一景點的概率是多少?請用畫樹狀圖或列表法加以說明,并列舉所有等可能的結果.
【解析】(1)該市周邊景點共接待游客數為15÷30%=50(萬人),A景點所對應的圓心角的度數是30%×360°=108°,B景點接待游客數為50×24%=12(萬人).
(3)畫樹狀圖如下:
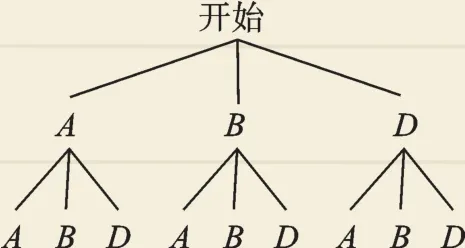
∵共有9種等可能結果,其中同時選擇去同一個景點的結果有3種,∴P(同時選擇去同一個景點)=
【點評】本題考查雙統計圖和概率計算等知識.在解題時要將兩個統計圖相互對應,讀取信息,正確計算、補圖,再運用樹狀圖或列表求同時選擇去同一個景點的概率.
江蘇省興化市戴澤初級中學)

