公路平曲線超高橫坡設計

蔣立華

(鹽城市交通規劃設計院，江蘇 鹽城 224000)

公路平曲線超高橫坡設計

蔣立華

(鹽城市交通規劃設計院，江蘇 鹽城 224000)

針對公路平曲線超高橫坡設計，采用二次拋物線過渡方式進行設計，在明確計算方法、驗證計算結果合乎技術標準的基礎上，分析其在具體工程中設計的方法。

公路平曲線；超高橫坡；橫向力系數；設計

1 公路平曲線超高橫坡設計

超高橫坡取值主要和橫向力系數等有關，選取合理的橫向力系數和超高橫坡，對公路彎道行車安全有重要作用，其中橫向力系數通常用μ表示，超高橫坡通常用i表示。公路彎道行車，因橫向力系數不斷變化，駕車人與乘車人會有不同的感受。在設計工作中，必須確保橫向力系數合理，只有在明確橫向力系數的基礎上才可以得到最佳的超高橫坡。本文按照規范指出的橫向力系數取值，并采用二次拋物線進行過渡，對公路平曲線超高橫坡實施解算。

橫向力系數存在以下關系式

i+μ=V2/127R

(1)

式(1)中：V表示車速；i表示超高橫坡；R表示公路平曲線的半徑；μ表示橫向力系數。

式(1)右側為彎道行車離心加速度，按照公式代入數據即可得出；左側為抵抗這一離心加速度的橫向力系數及超高橫坡。想要通過計算得出超高橫坡，需要知道橫向力系數及超高橫坡的實際分配。

考慮到超高橫坡和曲線曲率有正比例關系，最大的超高橫坡出現在曲線曲率的最大點，此時會使半徑較小的曲線有較大超高橫坡，而半徑較大的曲線卻有較小的超高橫坡，導致橫向力系數偏大，不符合規范要求；如果公路平曲線上的車輛均按照設計時速行駛，借助橫向力對離心力進行平衡，則在超高橫坡上升至最大值以后，余下離心力會改由橫向力承擔，可以解決上述情況下產生的缺陷，但在實際情況中，車輛實際速度通常很難和設計時速完全相同，應以通常情況下為研究對象，確保它們安全行駛。

圖1表示公路平曲線半徑和超高之間的關系與超高值設計計算，圖中的③是將②作為基礎通過改進獲得的，其中②表示的公路設計時速，而③為實際車速。圖中的④主要是在①、②間連接一條曲線，若曲線曲率相對較小，則可按接近③進行取值，借助一定超高橫坡對橫向力進行抵消。伴隨曲線曲率不斷增大，可以采取接近于最大超高進行超高設置，這樣可以很好的彌補以上方法存在的不足。

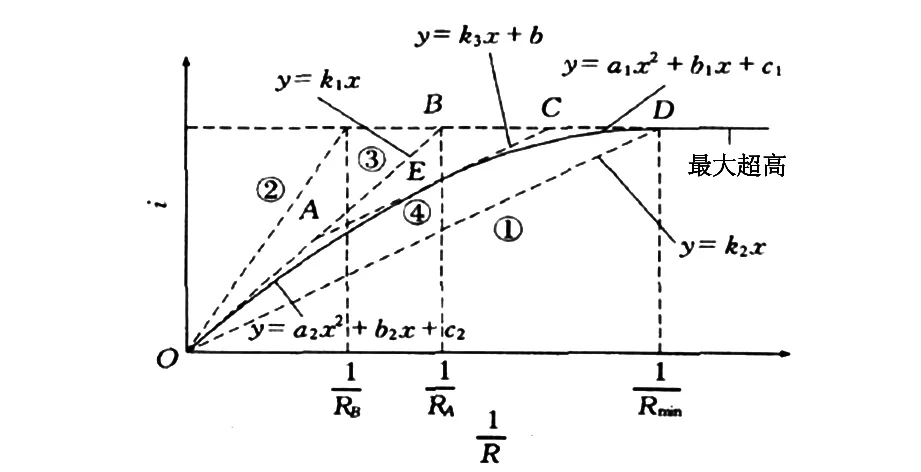
圖1 公路平曲線半徑和超高之間的關系與超高值設計計算

采用以下公式計算得出的RA表示在最大超高條件下當車輛μ等于0時的平曲線半徑。

RA=vA2/127imax

(2)

假設1/R和1/RA相等、i和imax相等，則對應圖1中的B點；假設1/R和1/Rmin相等、i和imax相等，則對應圖1中的D點。連接OB中點和BD中點，再于OAE與ECD處做兩條和直線保持相切位置關系的二次拋物線，此時二次拋物線縱坐標表示不同R值對應的設計超高。

公路平曲線實際車速取85 km/h，最大超高按8%計算，求取二次拋物線的方程。

1/R=127(i+μ)/vA2

(3)

若橫向力等于0，向式(3)中分別代入最大超高和實際車速可得RA為711.122 m；若橫向力取0.15，向式(3)中分別代入最大超高和實際車速可得Rmin為247.347 m。

分別求解y=k1x、y=k2x兩直線方程的k值，即k1為50.394、k2為19.198。在列出A點、C點和D點的坐標之后，采用A點和C點的坐標可以得出y=k3x+b直線方程的k3值和b值，即k3為19.198、b為0.025。根據A點和C點的直線方程，將1/RA代入，可得出其對應的縱坐標E(0.002,0.055)。

得到上述條件之后，可對y=a1x2+b1x+c1、y=a2x2+b2x+c2兩個二次拋物線進行求解。由于y=a1x2+b1x+c1和E點、D點相交，通過求導可得a1、b1和c1的值分別為-3 720.915、31.012和0.015，則其方程可表示為y=-3 720.915x2+31.012x+0.015，橫坐標取值區間為[1/RA，1/Rmin]；由于y=a2x2+b2x+c2和O點相交，通過求導可得a2、b2和c2的值分別為-9 825.544、50.394和0，則其方程可表示為y=-9 825.544x2+50.394x，橫坐標取值區間為(0，1/RA)。

又已知實際車速為80 km/h，由此可得出圓曲線半徑、超高值與橫向力系數相互關系(見表1)。

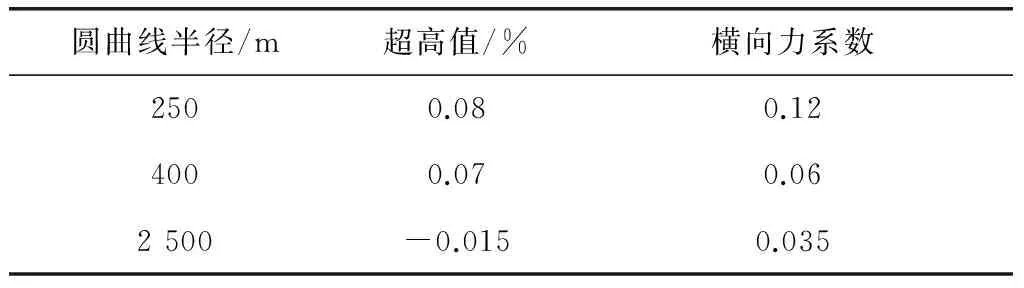
表1 圓曲線半徑、超高值與橫向

表1中，250 m為圓曲線的極限最小半徑，400 m為圓曲線的一般最小半徑，2 500 m為在不設超高條件下得出的半徑值。經驗證，上述結果和現行技術規范完全吻合。

2 公路平曲線超高橫坡設計運用

濱海縣火箭路建設工程的設計速度為60 km/h，最小平曲線半徑為650 m，一般路段道路橫坡為±2%。公路前后縱坡坡度在2%以內，超高值為8%，中小型車輛實際車速取80 km/h，最大橫向力系數取0.1，現對其超高橫坡進行設計。根據以上條件可分別得出兩條二次拋物線方程，即y=-28 569.672x2+90.709x+0.008，橫坐標取值區間為[1/1 417,1/650]；y=-44 640.061x2+113.386x，橫坐標取值區間為(1/5 500,1/1 417)。

在方程y=-28 569.672x2+90.709x+0.008的橫坐標中代入1/1 100可得超高橫坡為6.7%，相應橫向力系數為0.036。

大型車輛實際車速取85 km/h，當超高值等于8%時的圓曲線極限最小半徑為316 m，最大橫向力系數保持不變，則可得兩條二次拋物線方程，即y=-7 192.098x2+45.512x+0.008，橫坐標取值區間為(1/711,1/316)；y=-11 237.660x2+56.890x，橫坐標取值區間為(1/3 700,1/711)。

在方程y=-11 237.660x2+56.890x的橫坐標中代入1/1 100可得超高橫坡為4.4%，相應橫向力系數為0.01。

由于中小型車輛和大型車輛的實際車速不同，所以對應的超高橫坡也存在一定差別。若超高橫坡取7%，在式(1)中代入85 km/h，可得出橫向力系數為-0.02，說明這種情況下大型車輛行駛產生的水平分力大于離心力；同理，代入40 km/h后橫向力系數為-0.06，說明路面積雪時大型車輛行駛有向圓心處側滑的危險。因此，為確保大型車輛行駛安全，應適當降低超高橫坡；若超高橫坡取4%，在式(1)中代入120 km/h，可得出橫向力系數為0.06，滿足設計規范要求，但和設計時速為100 km/h情況下的700 m圓曲線最小半徑對應的橫向力系數相同，說明4%的超高橫坡取值較小，行車舒適度與安全性易受到影響。

綜合以上分析結論，建議該公路平曲線超高橫坡設置為5%。在這一超高橫坡條件下，當實際車速分別為120 km/h和85 km/h時對應的橫向力系數為0.05和0.02，可有效保證該路段行車安全及舒適度。

3 結 論

(1)若將摩阻力考慮為0，則要重點分析由行車速度差異造成的安全隱患，此時建議利用限制時速的方法，既要限制高速又要兼顧低速。

(2)長直線和半徑較小的曲線相連接時，因直線段車速較高，過渡至曲線后會產生很大離心加速度，為保證行車安全時應適當提高超高橫坡。

(3)車輛速度不同，在相同彎道上會產生不同離心加速度，如果存在多車道情況，則需在不同車道使用相適應的橫坡。

[1] 孫業香，吳立人.公路平曲線超高優化設計在工程實際中的運用[J].工程與建設，2014，(2):191-192+195.

[2] 嚴超群. 新建公路平曲線中的超高設計[J]. 中小企業管理與科技(上旬刊)，2013，(1):121-122.

[3] 王敬一，劉亞. 公路平曲線設計中的超高設計[J]. 科技資訊,2014，(26):99-100.

U412

B

1008-3383(2017)10-0019-02

2017-04-28

蔣立華(1982-)，男，工程師，研究方向：道路橋梁設計。