高校微積分課程教學方法探討

賀電鵬

(鄭州工商學院，鄭州 451400)

高校微積分課程教學方法探討

賀電鵬

(鄭州工商學院，鄭州 451400)

微積分是應用型本科高校會計類、經管類等專業的基礎課，但是當前的微積分教學存在諸多問題。從分析學生、因材施教，創新教學方法，理論聯系實踐、提高學習興趣和創新考核評價體系等四個方面對微積分教學進行思考和探討。

微積分；教學方法；評價體系

引 言

應用型本科高校即應用技術型本科高校，致力于培養應用型技術技能人才。專業課是培養應用型技術技能人才的重要途徑，微積分則是基礎課，是學習其他公共基礎課和專業課的基礎和前提。作為大學生在大學生涯最先接觸的一門課程，教好和學好微積分，幫助學生建立良好的學習習慣，樹立認真的學習態度，對學生構建微積分知識體系，掌握微積分的基本知識技能和后續學習其他公共基礎課和專業課都有重要意義。當前微積分的教學中存在諸多問題，教學現狀并不令人滿意，要想達到“教好”和“學好”微積分的目的，同時考慮到每屆學生的差異性，進行微積分課程教學方法改革勢在必行。

關于微積分教學改革，針對不同的側重點，各高校教師進行了大量的研究。針對多元函數微積分教學，多元函數微積分在講授概念、定理、計算時，適當與一元函數做結構類比，可降低教學難度，提升教學效果[1]；在進行偏導數與全微分教學時，結合一元函數導數的定義，類比給出多元函數偏導數的定義，可以幫助學生更好的理解多元函數偏導數的定義[2]。微積分課程中，微分的概念抽象難懂，不易理解，在講授該節內容時，利用案例導入可以把學生的注意力完全集中到本節課的學習中[3]。微積分的學習離不開練習，理論與實踐是相輔相成、密不可分的，重視微積分實踐——習題課，是學習微積分的必要步驟[4]。此外，在微積分教學中，考慮分層教學、引進數學建模、使用數學軟件等，也有很多人做了大量的工作[5]。總之，微積分課程教學改革，有著豐富而大量的研究。本文通過對微積分教學進行思考、探索和實踐，著重從“分析學生，因材施教”“創新多樣教學法”“理論聯系實踐、提高學習興趣”“創新考核評價體系”等四個方面進行闡述。

一、分析學生，因材施教

（一）學生特點和教學現狀

微積分的教學對象是大學一年級新生，新生剛剛經歷高考，處于從高中學習到大學學習的轉型階段，處于心理不成熟到心理成熟的過渡階段，處于獨立意識初現但缺乏自理自立能力的階段。作為一所應用型本科高校公共基礎課教學部的專職教師，通過對多屆學生微積分學習情況進行綜合分析，總結出應用型高校學生的學習現狀：數學基礎薄弱，高考成績100分以上的占比不到20%，90分以上的占比不到50%；對數學在一定程度上有天然的畏懼心理，沒有積極主動學習微積分的動力，學習微積分的主要目的就是通過期末考試；基礎好、學習主動性高和有志考研的學生比例偏低。這樣的學習現狀，不足以幫助學生構建微積分的知識體系，不足以幫助學生擺正學習微積分的心態，不能夠為后續課程的學習打好基礎。

（二）具體措施

分析學生需要全方位分析，不僅要認識學生的知識水平，還要知道學生的生活習慣、學習需求、畢業意向等。因此，在大學一年級講授微積分課程之前，可以做一個問卷調查。問卷設計要覆蓋學生的學習、生活、心理、需要等各個方面。對問卷數據進行分析，總結出學生的年代特點、知識特點、畢業意向、心理特點等，然后在定量分析學生的基礎上做到拉近師生距離，有的放矢的進行因材施教。

要做到因材施教，首先，教師應該以授課自然班為單位篩選出各個班的問卷，并就該班學生的數學基礎、學習習慣、智力特點、學習志向等進行分析。考慮到自然班的共同點和差異性，綜合制定教學目標和教學計劃。其次，在微積分授課過程中，教師的授課應該盡量覆蓋到班級各個層次的學生，讓各個層次的學生都能在微積分課堂上找到存在感，不要讓學生有被忽略的感覺。可以通過組織差異化座位，讓基礎好、善于學習、自制力強的學生與基礎不好、學習主動性不高的學生穿插就座，讓后者得以熏陶，促進微積分教學。最后，在布置作業和課后練習時，應該難易結合，盡量給更多的學生有做對題的機會，提升學生學習的信心。

二、創新教學方法

微積分教學方法多樣，本文從具體情況出發，在概念教學、多元函數教學、數學思想等方面進行創新教學。

（一）通過案例導入法進行概念教學

微積分課程中涉及很多的概念和定義，在概念教學中，如果生硬的將定義、概念強塞給學生，讓學生被動的接受，學生就會很難消化，會降低學生學習微積分的興趣甚至反感。微積分源于生活，作用于生活[3]。微積分的許多概念都是伴隨著生活中的實際問題而產生的，因此，在微積分概念授課時，介紹概念的背景或生活中的例子，可以讓學生自然過渡到微積分的概念學習中來，并進一步用所學概念去解釋生活中的實際問題。因此，在進行概念教學時，應該多尋找案例，在案例的基礎上總結出概念，做到概念源自實例，概念反作用于實例，讓學生自然而然的接受概念，認識概念，掌握概念。

例如，在函數微分的概念授課時，可以設計案例“一塊正方形金屬薄片，由于受溫度變化的影響，其邊長由x0變到△x，問此薄片面積改變了多少？”“sin45°=1，那么你能估算出 sin46°的值嗎？”[6]

通過案例的設計引入概念的基本模型，通過后一個案例的引入讓概念反作用于案例，并解決實際問題，可以讓學生更好的接受概念、理解概念、使用概念。

（二）類比法在多元函數中的教學

所謂類比法是指，根據事物1與事物2在某些屬性或結構上的相同或相似，而推出它們在其他屬性或結構上也相同或相似的推理方法，類比法是一種從已知特殊到未知特殊的推理方法，屬于一種兩個事物間的橫向遷移思維。[7]

類比法體現出來的數學類比思維是數學思維的一種重要形式。運用數學類比思維可以把未知的、陌生的對象和已知的、熟悉的對象進行對比，把結構相似的未知的事物和已知的事物進行對比，特別是在微積分多元函數教學時，概念復雜，受困于課時沒法詳細介紹背景，學生認知的資料少，學生總知識量有限等，還不足以對多元微積分的相關知識進行歸納、推理和演繹。因此，在微積分多元函數教學中使用類比法和數學類比思維，可以啟發學生的思路，為多元函數教學提供線索和思路，指導學生認識學習微積分課程[2]。

微積分課程多元函數的教學中，運用數學類比思維可以把陌生的多元函數的偏導數的概念和熟悉的一元函數的導數的概念進行對比，例如，二元函數偏導數定義的講解可以和一元函數導數的定義進行對比。運用類比法，可以把多元函數中未知的鄰域、二重極限和已知的一元函數的鄰域、函數極限相對比，例如，引進點函數u=f(p)，記多元函數u=f(x1,x2,...,xn)為點函數u=f(p)，讓它在結構形式上與一元函數y=f(x)一致，從而將一元函數中的鄰域和極限等定義和計算直接推廣到多元函數，降低學生學習多元函數的難度，有助于學生掌握多元函數的有關知識。運用類比法可以把多元函數中二重積分的分割、近似代替、求和、取極限與醫院函數定積分的分割、近似代替、求和、取極限做類比，定積分的表達式

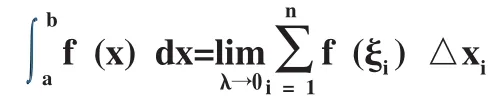
與二重積分的表達式

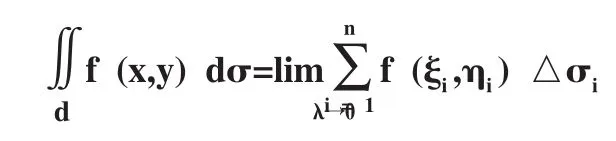
在結構上是一致的，二重積分的定義與定積分的定義類比有助于學生理解更復雜的二重積分的定義。[1][6][8]

（三）宏觀把握微積分、構筑微積分知識體系

系統的學習可以幫助學生學習課程的知識點和知識細節，及時的總結可以幫助學生跳出具體的知識點，從宏觀上把握微積分的知識結構，構筑微積分課程的知識體系。

微積分是在函數知識的基礎上，引入極限概念并以極限為最基本的工具，介紹一元函數微積分、多元函數的微積分、無窮級數和微分方程與差分方程的相關知識。一元函數微積分主要是以極限為工具研究函數的導數與微分、微分中值定理與導數的應用以及一元函數的不定積分和定積分的內容；多元函數微積分與一元函數知識體系類似，主要是以二元函數為例介紹二元函數的概念、二元函數的極限、多元函數的偏導數與全微分、多元復合函數與隱函數的微分法、多元函數的極值與最值以及二元函數的二重積分。無窮級數是表示函數、研究函數性質和數值計算的有力工具，主要介紹常數項級數的概念與性質、正項級數和任意項級數斂散性的判別以及冪級數和函數的冪級數展開。微分方程與差分方程主要介紹了簡單的微分方程和差分方程的基本理論。[6][8]

三、理論聯系實踐，提高學習興趣

大學微積分緊張的課時，大量的教學內容，很容易讓微積分課堂進入“填鴨式”的課堂，循環往復的新內容講授容易讓學生產生疲憊感，降低學生的學習興趣。因此，在微積分的教學過程中，需要理論聯系實踐，將數學最大的實踐——習題課引進課堂，豐富學生的視野，提高學生的興趣。

講授完一個完整的章節，意味著一部分相對獨立的微積分知識的結束，學生在學習的時候肯定有諸多的問題，習題課可以集中解決學生關心的問題，幫助學生理解和鞏固所學知識。習題課的教學宗旨是：通過問題討論、例題演示和解題技能及技巧的訓練，以期學生加深對基本概念的理解，提高論證、運算和應用能力，并配合講授課共同完成教學規定的要求[4]。習題課的設計應該兼顧多個方面，首先應該系統總結本部分的知識體系和知識點構成，幫助學生構建本章節的知識輪廓；其次應該幫助學生解決作業的問題，糾正學生的不良學習習慣；最后應該幫助學生發散知識內容，擴展視野，貫通知識連結點，提高學生的學習興趣。

四、創新考核評價體系

根據應用型高校的實際情況建立起一套科學完備的適合應用型高校的微積分課程的教學考核評價體系，可以更好的促進微積分課程在應用型高校的教學，更好的促進應用型高校的學生學習微積分課程。教學考核評價體系分兩個方面：對學生的考核評價和對教師的考核評價。對學生而言，單單只是通過卷面的分數進行考核是不合理也不完全的，高校可以通過鼓勵在校學生做創新性研究，如發表微積分相關的文章、微積分實用的案例分析等，將這些創新性研究按照一定的比例納入學期考核，使得考核內容多樣化。其次，可以將學習筆記納入考核，督促學生學有所記，記有所學。對教師而言，可以讓學生參與到教師教學考核評價中，將學生對教師的評價納入教師考核評價體系，這樣可以衡量教師教學過程中是否認真負責，可以及時發現學生學習的問題所在，可以督促教師帶領學生學習微積分[5]。

總之，微積分教學在現代大學數學體系中占有重要的位置，是眾多的交叉科學中的重要組成部分，是相關專業專業課學習的基礎課程。因此，采取有效的教學對策對提高微積分教學的效果是十分必要的。

[1]閔蘭，陳曉敏.結構類比在多元微積分教學中的應用[J]．西南師范大學學報（自然科學版），2015（10）：187－190.

[2]馮閃，王海燕.類比方法在偏導數與全微分教學中的應用[J].產業與科技論壇.2010，9（6）：175-177.

[3]趙翠新.用案例導入法進行微分概念的教學[J].赤峰學院學報（自然科學版），2016，32（12）：1-3.

[4]杜耀剛.重視數學實踐性環節——習題課[J].北京電子科技學院學報，1996，4（1）：14-17.

[5]劉家保，陸一南.大學微積分課程改革的研究與實踐[J].長春大學學報，2012，22（06）：738-740.

[6]龔德恩，范培華.微積分[M].高等教育出版社，2012:31-321.

[7]冀東江.類比思想對大學數學知識遷移的影響[J].高教學刊，2016（06）：102-103.

[8]同濟大學數學系.高等數學[M].高等教育出版社，2014：3-96.

The Discuss of Teaching Methods on the Differential and Integral Calculus Course

HE Dian-peng
(Zhengzhou Technology and Business University,Zhengzhou Henan451400,China)

The Differential and Integral Calculus Course is the basic course of accounting,management and other majors in applied undergraduate colleges.the research shows that there are many problems in the current teaching.This paper analyzes and discusses calculus teaching from four aspects:analyzing students,teaching students in accordance with their aptitude,innovating various teaching methods,linking theory with practice,improving learning interest and innovating assessment system.

calculus;teaching methods;evaluation system

G642

A

1671-1084（2017）06-0068-04

DOI 10.16221/j.cnki.issn1671-1084.2017.06.016

2017-04-06

賀電鵬，碩士，鄭州工商學院公共基礎課教學部講師，研究方向為非線性微分方程。