論銳角三角函數(shù)概念教學(xué)

周小云

[摘? 要] 在實際教學(xué)中，很多老師教學(xué)銳角三角函數(shù)的概念過于簡單，絲毫未觸及函數(shù)的本質(zhì)，更未體現(xiàn)銳角三角函數(shù)的函數(shù)特性. 基于此，本文對初中銳角三角函數(shù)概念教學(xué)方法做了詳細闡述，希望對同行有一定的參考、借鑒作用.

[關(guān)鍵詞] 銳角三角函數(shù);概念;教學(xué)

對于初中銳角三角函數(shù)的概念，最常見的教學(xué)方法是：根據(jù)課本講解銳角三角函數(shù)的定義. 比如教學(xué)正弦函數(shù)時，先下定義：在直角三角形中，銳角∠A的對邊比斜邊，叫∠A的正弦函數(shù)，記作sinA=■，然后通過練習(xí)加以鞏固. 殊不知，這種教法只能讓學(xué)生記住定義，其完全背離了數(shù)學(xué)教育的初衷——發(fā)展學(xué)生的邏輯思維，培養(yǎng)學(xué)生的數(shù)學(xué)思維品質(zhì). 這樣處理教材的方式膚淺、死板，根本不能讓學(xué)生體會到銳角三角函數(shù)的函數(shù)特性. 筆者經(jīng)過多年的實踐摸索，發(fā)現(xiàn)了一套銳角三角函數(shù)概念的教學(xué)方式，其不僅成功避免了尋常膚淺、死板的教學(xué)方式，還很有效果，現(xiàn)介紹如下.

奠定一個基礎(chǔ)

先奠定一個基礎(chǔ)——在直角三角形中，當銳角一定時，不論三角形的大小怎樣變化，任何兩邊之比都是一個定值，然后為后面研究“兩邊的比值隨角度變化”服務(wù). 奠定這個基礎(chǔ)應(yīng)堅持一個原則，即教師作圖，學(xué)生觀察，教師引導(dǎo)學(xué)生分析，由學(xué)生自己得出結(jié)論. 切忌教師代替學(xué)生思考，切忌由教師得出結(jié)論. 試想，如果學(xué)生連這個基礎(chǔ)都沒奠定，那后面研究變化的過程時該從何談起？

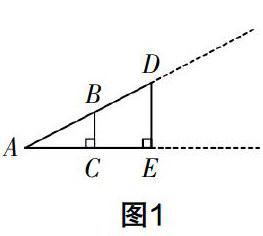
這個過程可以這樣處理：教師先給出圖1，從靜態(tài)的角度觀察圖1，引導(dǎo)學(xué)生做出如下推理.

在Rt△ABC和Rt△ADE中，因為∠A=∠A，∠ACB=∠AED=90°，所以△ABC∽△ADE. 所以AE/AC=DE/BC. 不妨設(shè)AE/AC=DE/BC=k，k為相似比，則AE=kAC，DE=kBC. 所以DE/AC=kBC/kAC=BC/AC.

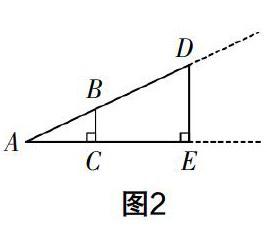
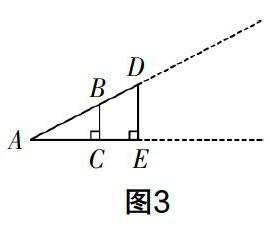
在圖1的基礎(chǔ)上，教師再給出圖2和圖3，保持Rt△ABC的大小不變，從動態(tài)的角度觀察圖形，引導(dǎo)學(xué)生認識到Rt△ADE的大小在不斷地變化. 圖2中的Rt△ADE在圖1的基礎(chǔ)上放大，圖3中的Rt△ADE在圖1的基礎(chǔ)上縮小. 研究發(fā)現(xiàn)，無論Rt△ADE是放大，還是縮小，DE/AC的值總等于BC/AC的值. 因為在整個變化的過程中，Rt△ABC的大小保持不變，所以BC/AC的值不會變. 于是可以得出結(jié)論：在直角三角形中，當銳角一定時，無論三角形的大小怎樣變化，這個銳角的對邊與鄰邊的比是一個定值.

如果有條件，上述過程可借助幾何畫板、動態(tài)作圖來教學(xué)，這樣的話，學(xué)生可以直接參與操作，易于理解和接受;不具備現(xiàn)代教學(xué)條件的，教師要在黑板上畫圖，但畫圖時必須體現(xiàn)圖形的動態(tài)變化.

從一個點突破

在直角三角形中，邊與邊的情況有好幾種，選擇一種情況來突破，不僅效果好，而且效率高. 這是因為：（1）幾種情況一起講，難以講清楚. 即使能講清楚，容易相互干擾，學(xué)生也難以全部接受，倒不如抓住一種情況來進行教學(xué). （2）銳角三角函數(shù)的幾種對應(yīng)關(guān)系很類似，所以可以根據(jù)前面奠定的基礎(chǔ)，選擇一種情形來突破. 比如，前面已經(jīng)奠定“在直角三角形中，當銳角一定時，無論三角形的大小怎樣變化，這個銳角的對邊與鄰邊的比是一個定值”這一基礎(chǔ)，此時就可以選擇“對邊比鄰邊”來進行教學(xué).

體現(xiàn)“函數(shù)味”

在初中函數(shù)教學(xué)中，我們應(yīng)培育學(xué)生樹立相互聯(lián)系、運動發(fā)展的數(shù)學(xué)理念，在動態(tài)的思維模式中掌握函數(shù)知識的基本要領(lǐng). 函數(shù)的本質(zhì)是描述在一個變化的過程中，兩個變量之間緊密關(guān)聯(lián)、相互依存的關(guān)系，一個變量隨著另一個變量的變化而發(fā)生變化. 不妨設(shè)其中一個變量為x，另一個變量為y，對于每一個x，y都有唯一的值與之對應(yīng)，則y是x的函數(shù)，其中x是自變量，y是因變量.

在初中數(shù)學(xué)銳角三角函數(shù)中，哪個是自變量，哪個是因變量呢？我們還是先引領(lǐng)學(xué)生觀察變化過程. 教師給出圖4，因為“在直角三角形中，當銳角一定時，無論三角形的大小怎樣變化，這個銳角的對邊與鄰邊的比是一個定值”，即邊的比值與直角三角形的大小無關(guān). 為了研究方便，不妨把AC的長度固定下來，這樣BC/AC的值就取決于BC的大小. 因為是研究變化過程，所以以圖4為基礎(chǔ)圖，從動態(tài)角度去作圖：圖4中的點B是控制點，可以上下拖動，從而改變直角三角形中的元素. 在圖4的基礎(chǔ)上，將點B往上拖（如圖5），此時∠BAC變大，BC邊變長;將點B往下拖（如圖6），此時∠BAC變小，BC邊變短. 在拖動點B的變化過程中，只要點B的位置改變，∠BAC的大小就會發(fā)生改變，BC邊的長也發(fā)生改變. 而且，對于∠BAC的任何一個大小，BC邊都有唯一的長度與之對應(yīng). 此時，可引導(dǎo)學(xué)生完整地表述：在這個變化過程中，BC/AC的值隨著∠BAC的變化而變化，且對于∠BAC的任何一個值，BC/AC都有唯一的值與之對應(yīng)（可見，符合函數(shù)定義），所以BC/AC是∠BAC的函數(shù). 這里可以考慮向?qū)W生指出：在這個變化的過程中，BC/AC是創(chuàng)造的變量，原本的變化過程中并沒有這個變量.

接著引導(dǎo)學(xué)生思考：怎樣表示剛才發(fā)現(xiàn)的這個函數(shù)關(guān)系呢？接下來再引出：數(shù)學(xué)中規(guī)定，用“tan∠BAC=BC/AC”來表示這種關(guān)系. 在∠BAC不引起歧義的前提下，還可以去掉角的符號和另外兩個字母，直接表示為“tanA=BC/AC”. 此時，可以由學(xué)生自己判斷，在這個函數(shù)關(guān)系中，哪個是自變量，哪個是因變量.

以點帶面

在講清正切函數(shù)的基礎(chǔ)上指出正弦函數(shù)、余弦函數(shù)與正切函數(shù)類似，只是“不同的邊進行相比”，再給正弦函數(shù)、余弦函數(shù)下定義. 這種以點帶面的處理方式，一是思路清晰，教法干練;二是高效，避免重復(fù)啰唆;三是符合人類認知事物的一般規(guī)律，還能發(fā)展學(xué)生的類比分析能力.

概念鞏固

概念鞏固通常需要從正、反兩方面來加強. 對于銳角三角函數(shù)的正面加強，可以考慮如下方式：（1）解釋概念名稱. 比如解釋“正切”可以這樣處理：“正”，是指角正對的邊，即對邊，“切”，可讓學(xué)生聯(lián)想在家做飯時切菜的姿勢，與菜斜著時用刀，叫“削”，與菜垂直時用刀，叫“切”，所以“切”表示“垂直關(guān)系”. 這樣既生動形象，又與學(xué)生的實際生活聯(lián)系了起來.（2）正面應(yīng)用定義，利用定義來解題. 比如計算30°等特殊角的三角函數(shù)值.

對于銳角三角函數(shù)概念的反面加強，常用的方法是給出錯誤的應(yīng)用，讓學(xué)生去分析、判斷. 比如如圖7，在Rt△ABC中，∠C=90°，AB=10 cm，BC=6 cm，請判斷下面的說法是否正確：①sinB=AC/AB;②sinA=0.6 cm. 比如如圖8，∠ABC≠90°，請判斷sinA=BC/AC是否正確. 比如如圖9，Rt△DEF∽Rt△ABC，且相似比k=DE/AB=2，請判斷sinB=1/2sinE是否正確.

這種銳角三角函數(shù)教學(xué)處理方式，注重數(shù)學(xué)知識本身的特性，注重學(xué)生思維品質(zhì)的培養(yǎng)，注重學(xué)生能力的發(fā)展，不僅能引導(dǎo)初中生對三角函數(shù)有一個清晰、準確的認識，而且能為高中學(xué)習(xí)任意三角函數(shù)知識積累研究經(jīng)驗，打下堅實的理論基礎(chǔ).