多方同時簽名方案的算法

(山東科技大學數學與系統科學學院 山東 青島 266590)

多方同時簽名方案的算法

李彥

(山東科技大學數學與系統科學學院山東青島266590)

同時簽名方案是在群簽名的基礎上發展而來的一種數字簽名方案，大部分同時簽名方案是基于雙線性對，并且參與簽名的對象只有兩方。通過寫多方同時簽名方案的算法，了解簽名方案的形式以及方案的安全性。

橢圓曲線；同時簽名；公平交換

一、前言

2004年，由Chen，Kudla以及Paterson[1]共同提出了同時簽名方案的概念，即參與簽名的兩方在沒有第三方的幫助下，進行交互完成對各自信息的簽名。簽名發起方掌握關鍵數，在簽名者公開關鍵數之前，就所有第三方角度看來，對于信息的簽名都是匿名的，當關鍵數公開，簽名即與各自簽名者綁定。2012年，Ye Qing等人[2]研究了關于完美同時簽名的方案，提出了一個新的隱私保護PCS協議。2013年，孟雷[3]對橢圓曲線密碼學進行了系統的歸納，并在此基礎上提出了一種混合加密系統，大大提升了安全性。2014年，Xiao Tian等人[4]又對多方同時簽名進行了拓展，在此之前沒有較為安全的模型用于多方同時簽名，Xiao Tian等人構造了一個新的MCS，與已有的方案相比，具有更高的安全性與更低的計算量。2015年，Xiao Tian等人[5]又提出在無隨機預測情況下的同時簽名方案。

二、多方同時簽名方案的算法

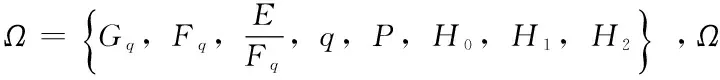
簽名者IDi隱藏自身身份信息IDi，計算Qi=H0(IDi)并公開Qi，然后簽名者IDi進行以下步驟：

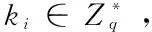
(2)IDi計算di=ki+kiH1(Si)，Pi=kiP；

(3)計算dimodq，若結果為0，則返回(1)，否則輸出簽名者IDi的私鑰Di=(di,Si)，公鑰Pi.

(1)計算Zi=ziQi；

(2)計算fi=H1(Zi)；

輸出關鍵數像fi.

簽名者IDj輸入簽名信息mj，私鑰Dj=(dj,Sj)，公鑰Pj，關鍵數像fj并進行以下步驟：

(2)計算hi=H2(mj,fjPi,Yj,Si)，tj=H2(mj,fjPi,Yj,QjH1(Sj))；

(4)計算Vjmodq，如果為0，返回步驟(1)；

得到σj=(rj,Vj)，輸出簽名者IDj對于簽名信息mj的模糊簽名δj=(σj,Q1,…,Qn,Yj,mj).

驗證：驗證者接收到簽名者IDj對于簽名信息mj的模糊簽名δj=(σj,Q1,…,Qn,Yj,mj)后進行以下步驟：

(1)驗證rj,Vj為[1,q-1]中的整數；

(2)計算hi=H2(mj,fjPi,Yj,Si)，tj=H2(mj,fjPi,Yj,QjH1(Sj))；

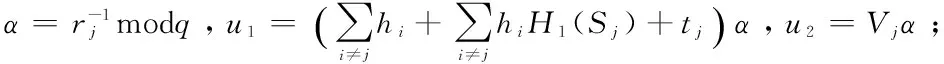
(4)計算X=u1Pj-u2P=(x1,y1)，如果x1modq=0,則拒絕簽名，輸出“No”，否則計算v=x1modq，當且僅當v=rj時接受簽名，輸出“Yes”。

三、安全分析

(一)不可偽造性

攻擊者偽造簽名者簽名δi(i=1,2,…,n)，因為不知道簽名者私鑰Di，所以成功的可能性是可忽略的。

(二)匿名性

在簽名者公布關鍵數之前，所有的簽名在任何第三方角度看來都是模糊的。分析：簽名算法中，簽名者IDj是隨機選擇的yj，而且hi,tj中所有元素也是全部公開的，因此在簽名者公布關鍵數之前，所有的簽名就任何第三方角度看來都是模糊的。

四、結束語

本方案中的算法還存在些缺陷，因為簽名發起者在方案中仍然占有一定的優勢，但是算法的出現使得我們了解方案如何進行，在以后如何提高安全性有很大的幫助。

[1]Liqun Chen,Caroline Kudla,Kenneth G.Paterson.Concurrent Signatures[C].Advances in Cryptology-EUROCRYPT,2004:287-305.

[2]Ye Qing,Zheng Shihui,Guo Hongfu,Yang Yixian.Generalization of Perfect Concurrent Signatures[J].ScienceDirect,2012,19(6):94-104.

[3]孟雷.基于橢圓曲線的密碼系統研究[D].哈爾濱：哈爾濱工業大學，2013年.

[4]Xiao Tian,Qiong Huang,Duncan S.Wong.Extending Concurrent Signature to Multiple Parties[J].Theoretical Computer Science,2014,548:54-67.

[5]Xiao Tian,Qiong Huang,Duncan S.Wong.Concurrent Signature Without Random Oracles[J].Theoretical Com——puter Science,2015,562:194-212.

李彥(1989.10-)，女，漢族，山東省菏澤市人，山東科技大學數學與系統科學學院碩士研究生在讀，研究方向信息安全。